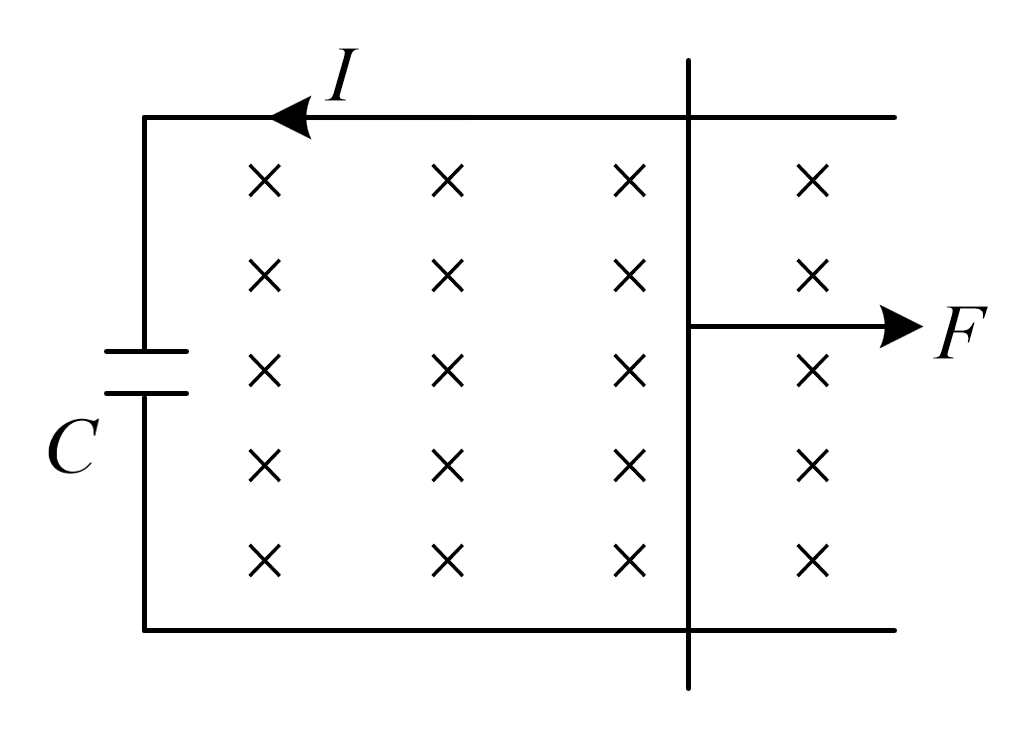
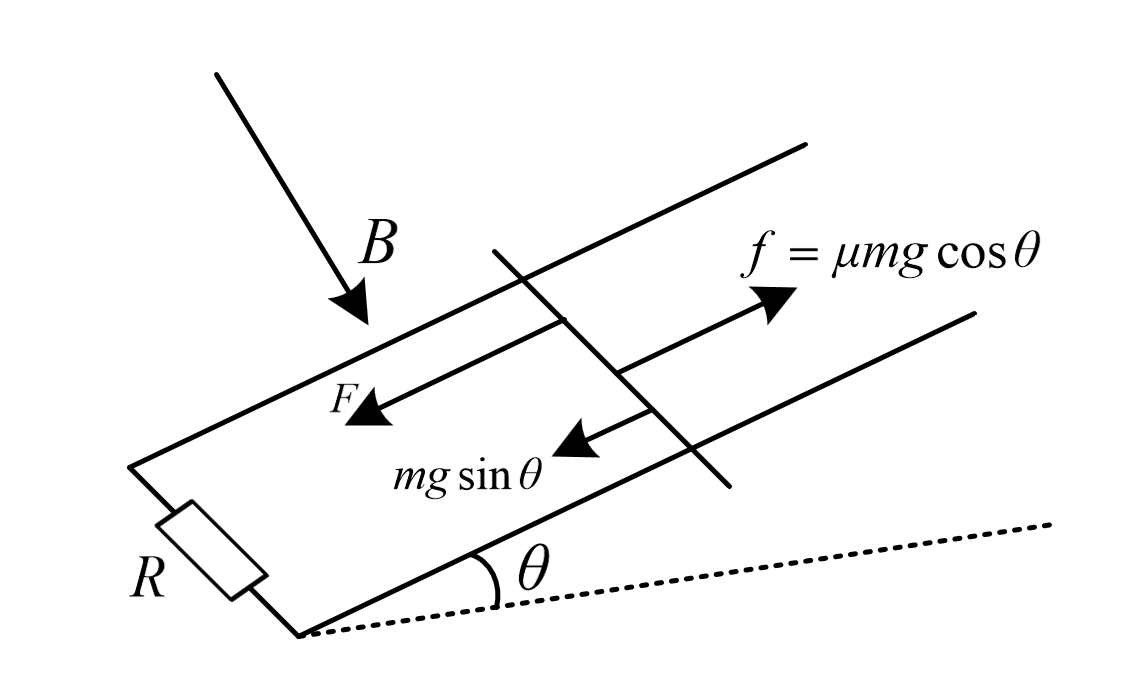
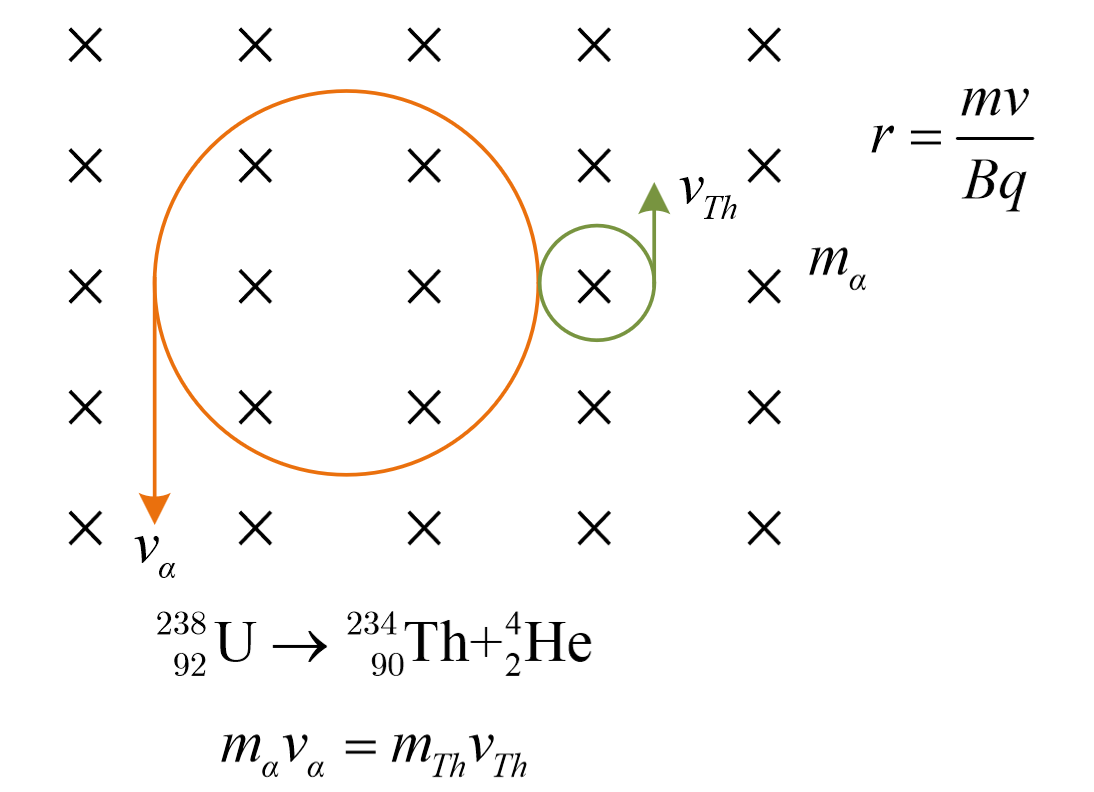
高中/数学/解析几何
解析几何
椭圆
第一定义
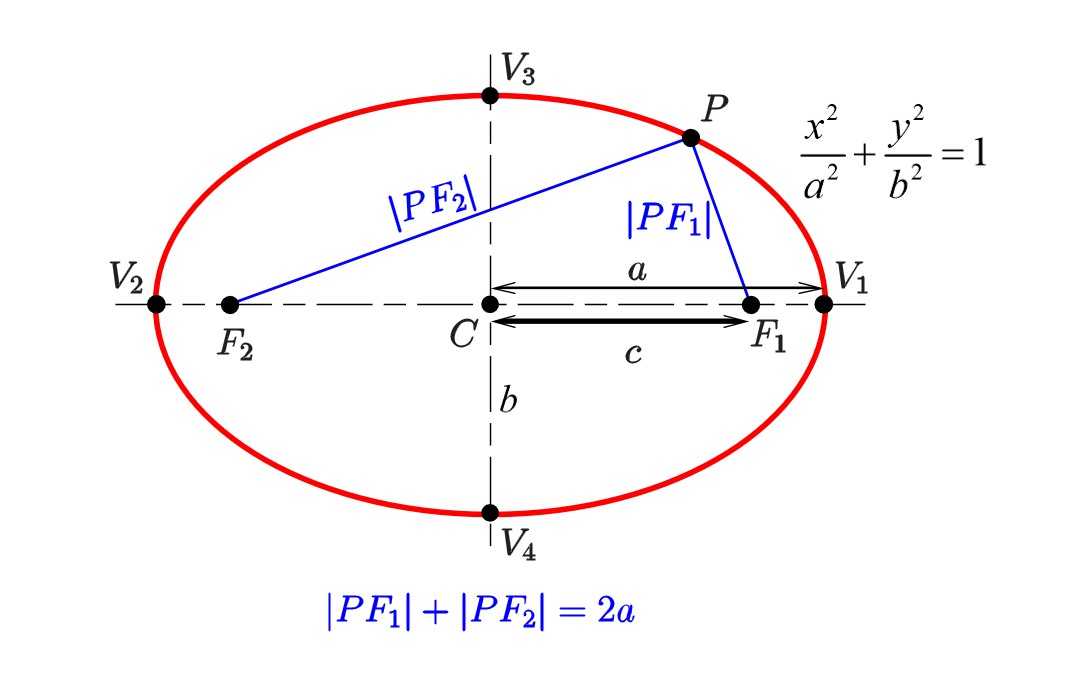
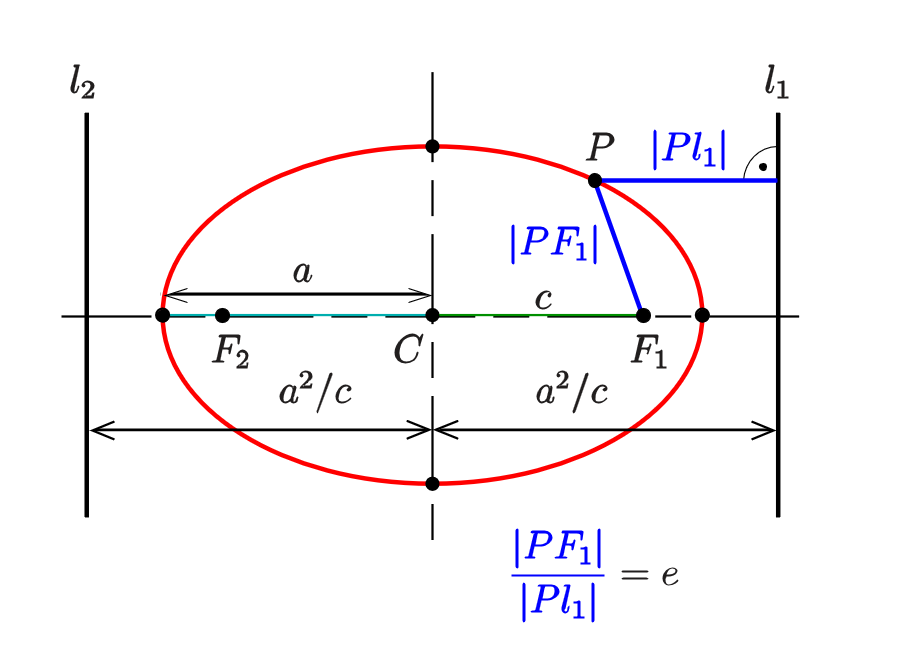
第二定义
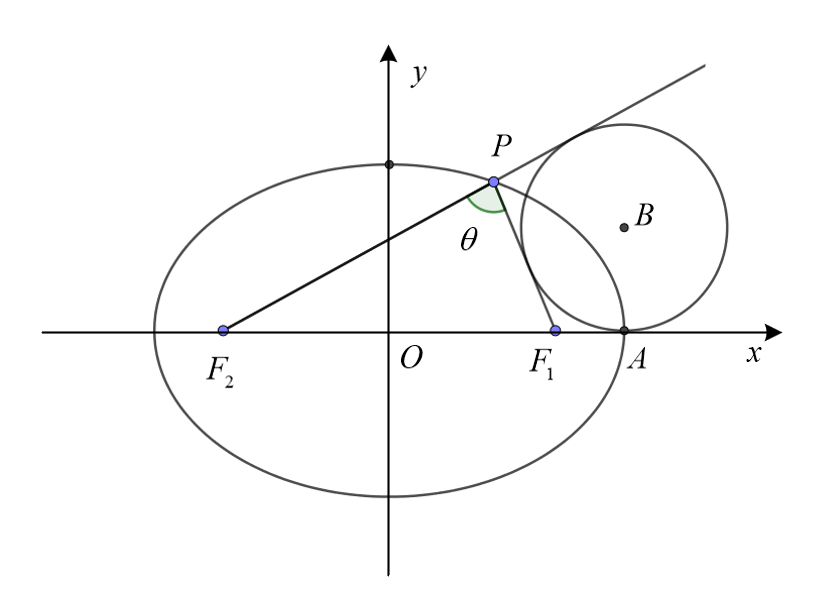
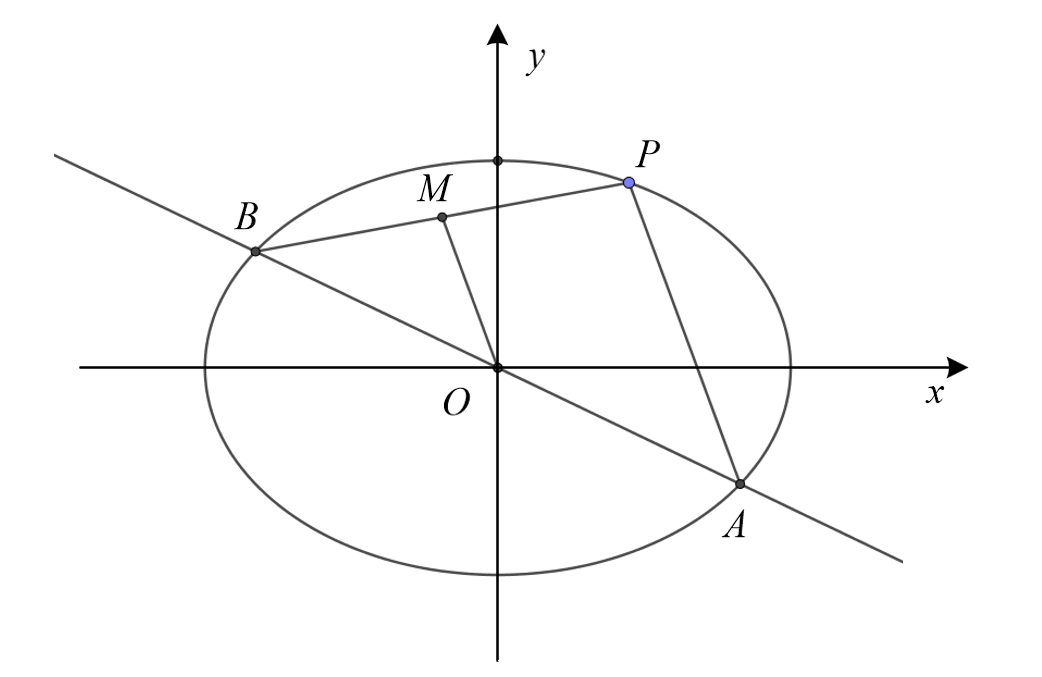
第三定义
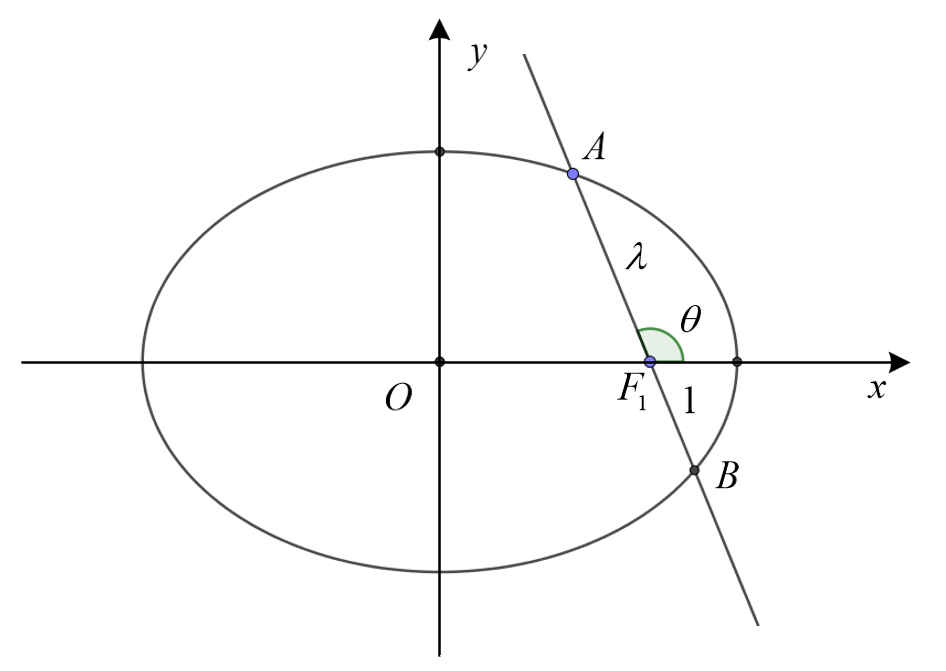
极坐标
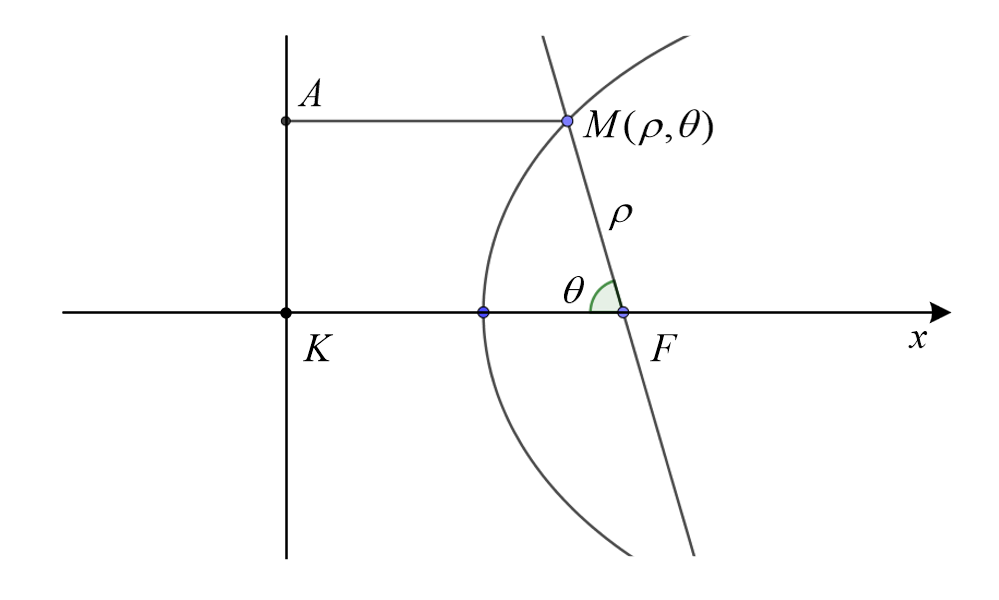
参数方程
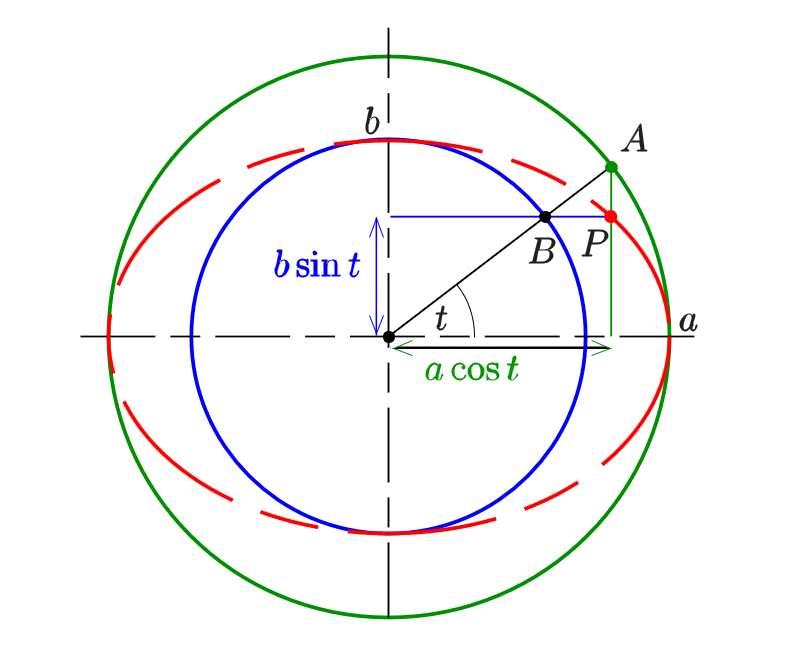
双曲线
第一定义
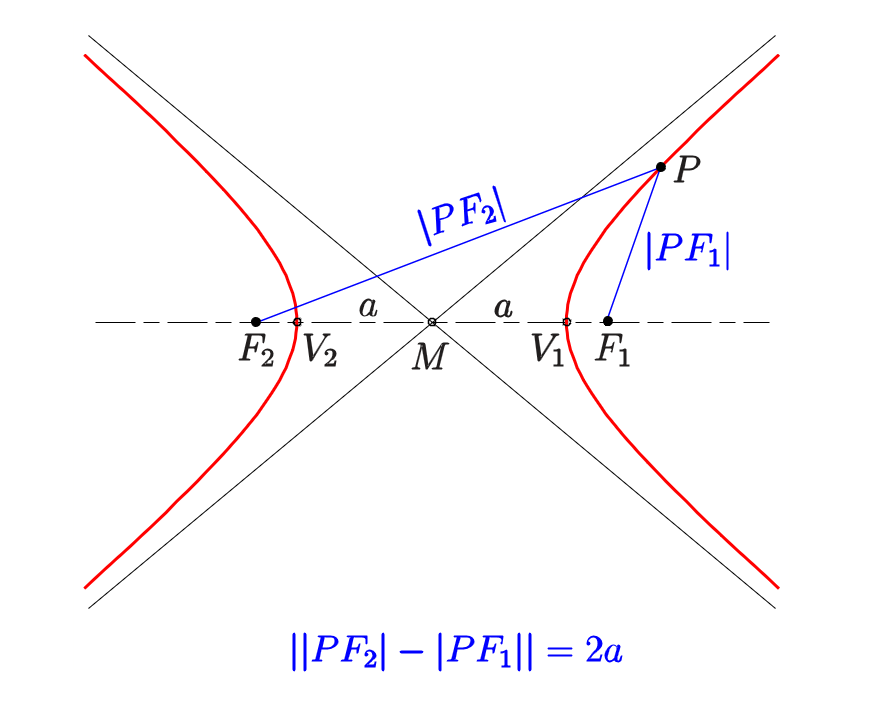
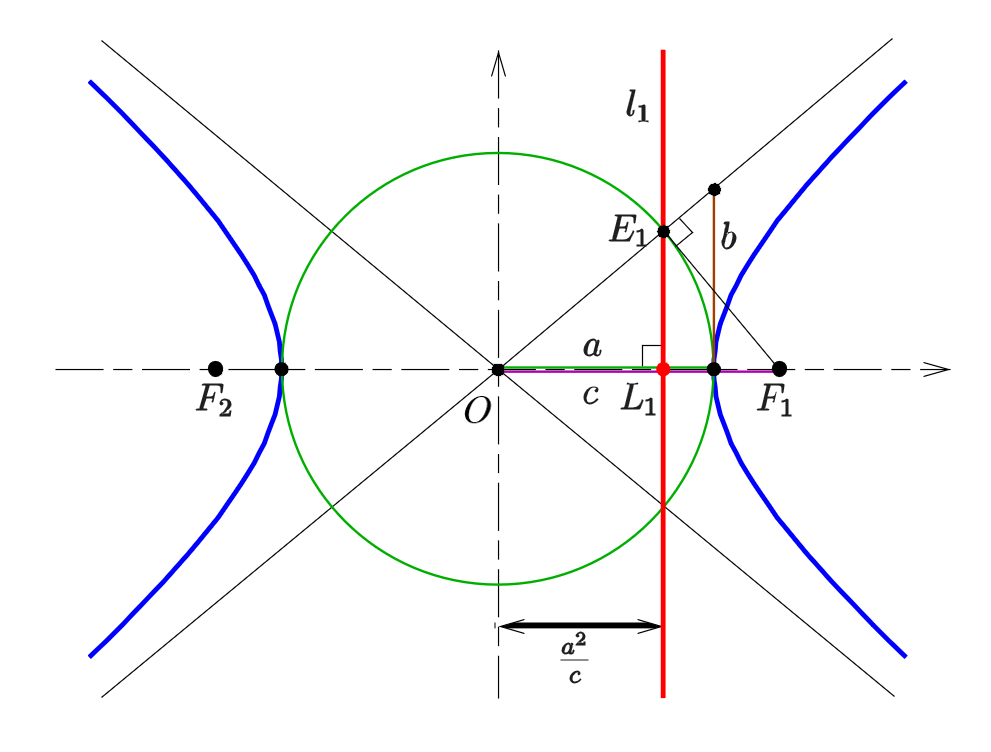
第二定义
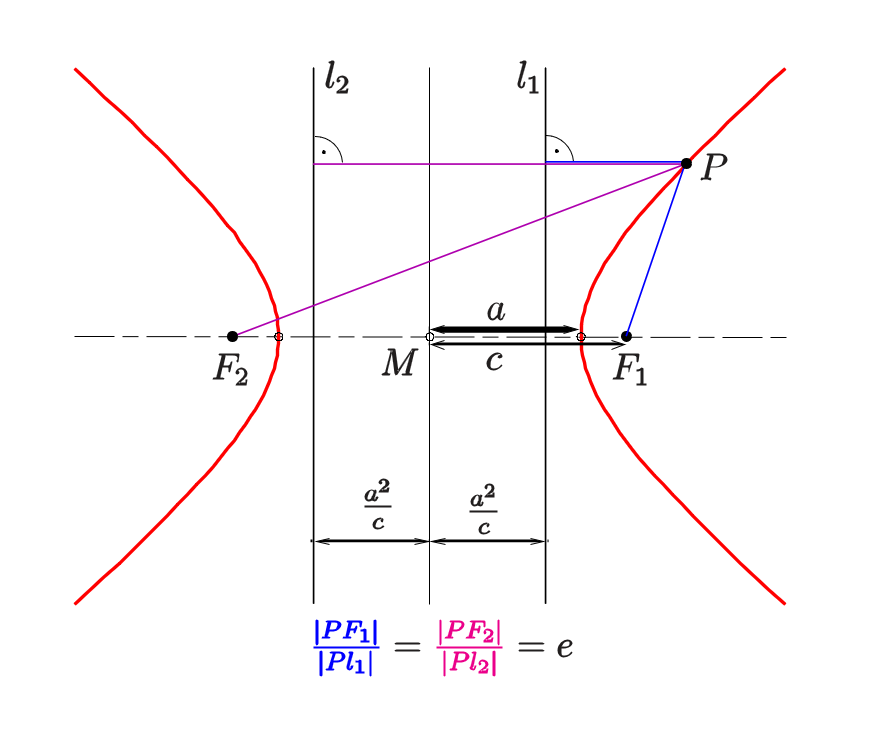
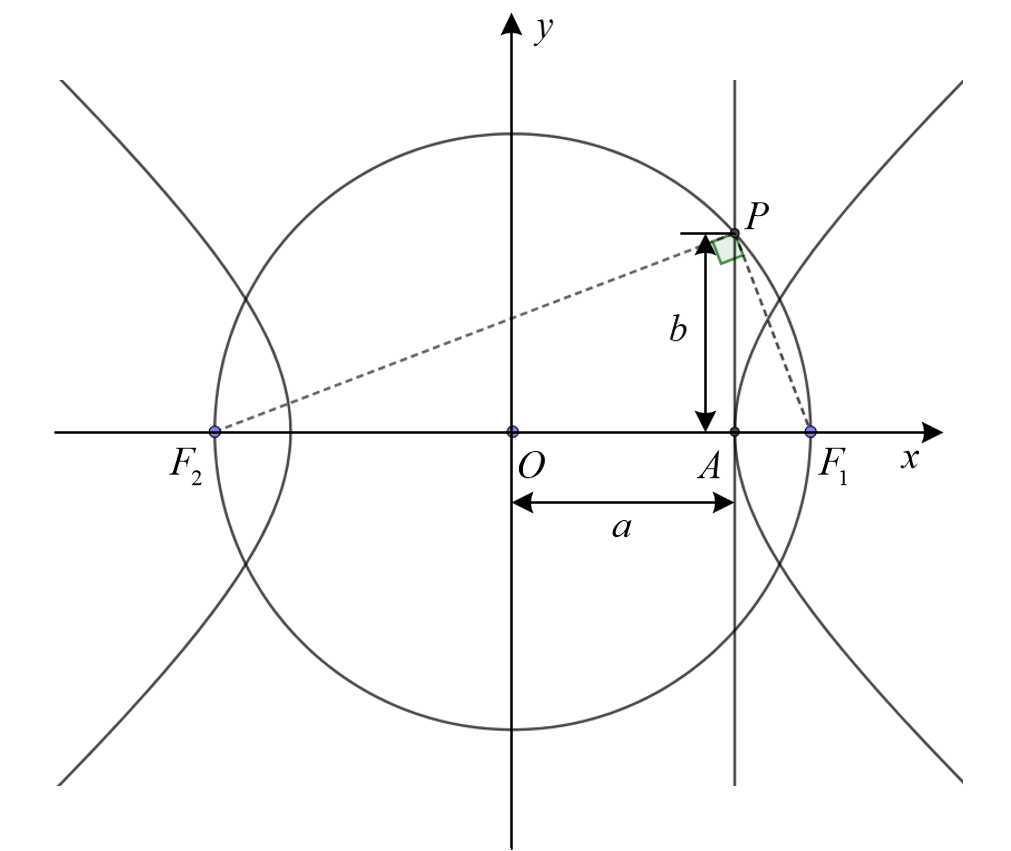
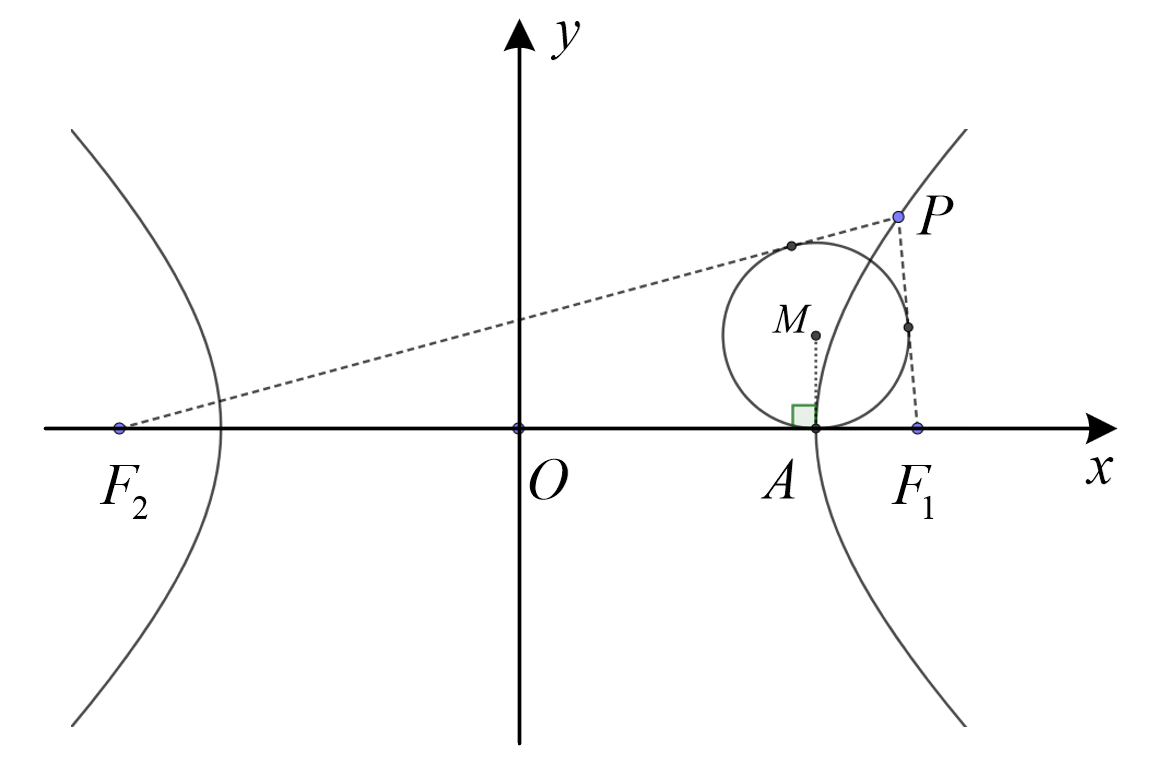
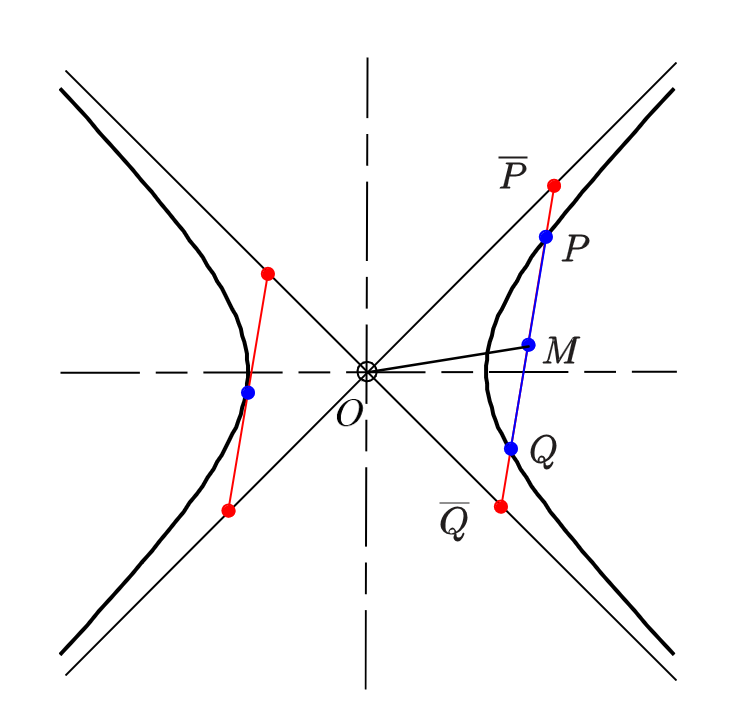
性质
抛物线
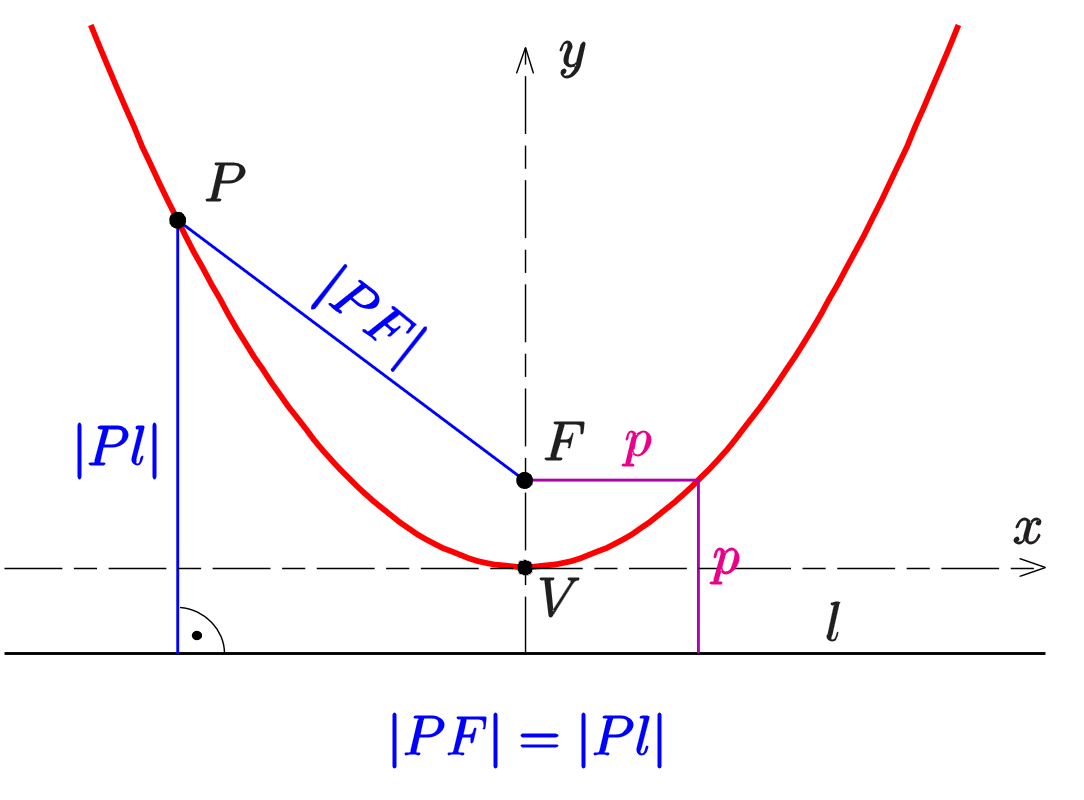
焦点弦
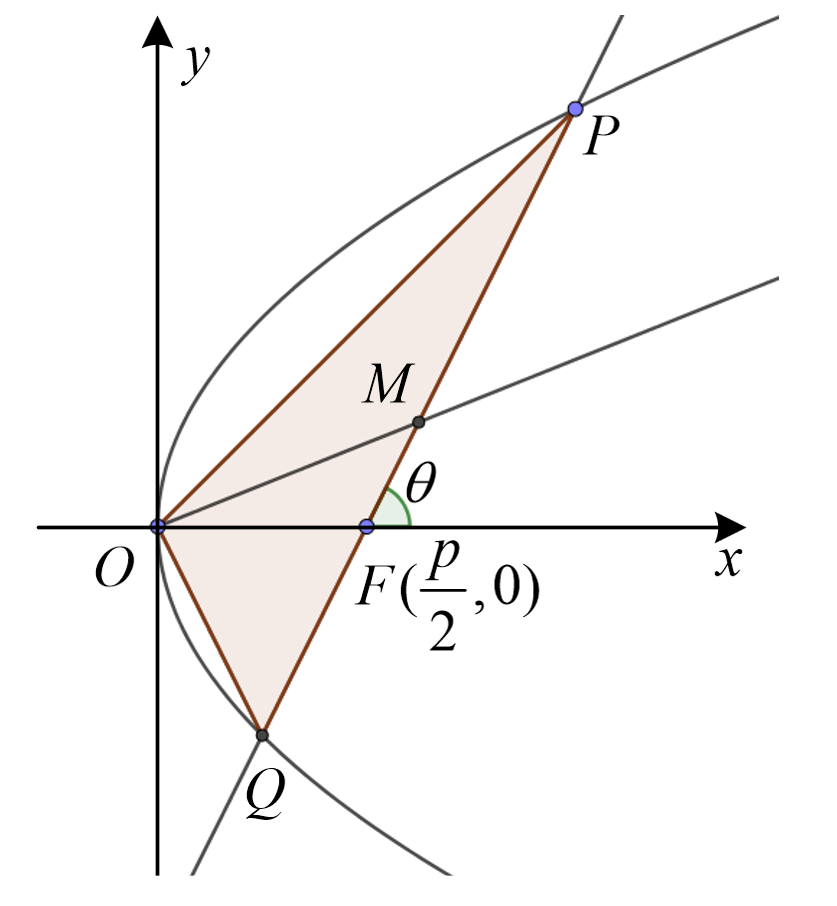
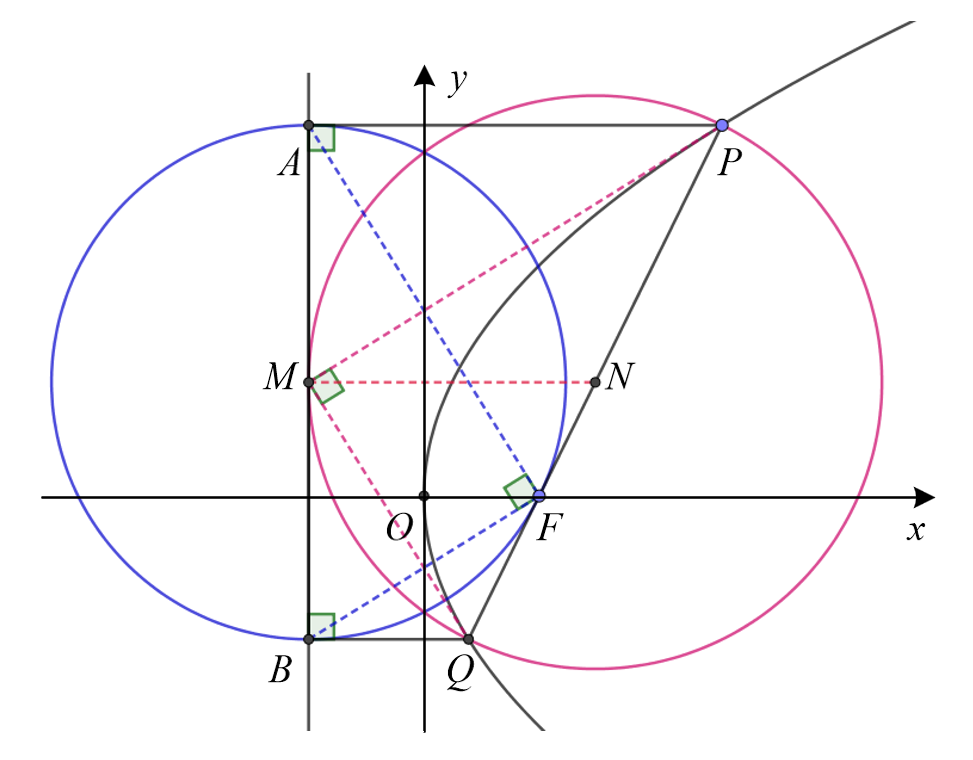
参数方程
切线
切线方程为
抛物线
双曲线
椭圆切线
双曲线切线
不包括斜率不存在时
$P({x_0},{y_0})$在切线上,解出$k$
若$k^2$前系数为$0$,则为一次方程,有一条斜率存在的切线,还有一条不存在的切线
若$k^2$前的系数不为$0$,则该方程是一个关于$k$的一元二次方程,可能有$0$个,$1$个,$2$个解
若$\frac{x_0^2}{a^2} - \frac{y_0^2}{b^2}=0$,有一根为$k=\frac{b}{a}/ - \frac{b}{a}$,故舍去
高中/前川定理
前川定理(The Maekawa-Justin Theorem)
简介

MAEKAWA Jun (前川淳),日本的软件工程师,数学家,折纸艺术家。
平顶点折叠的例子
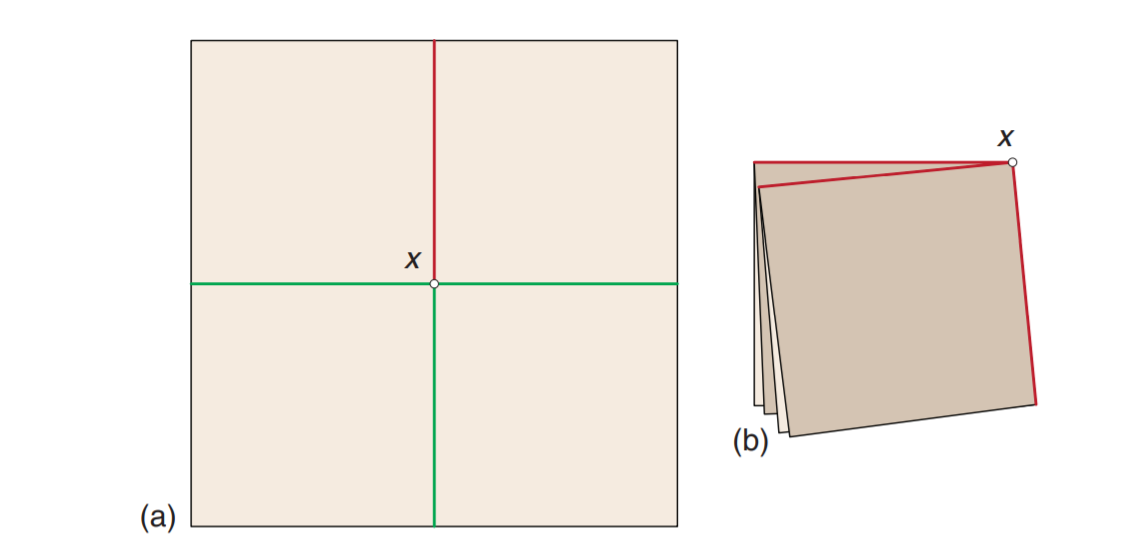
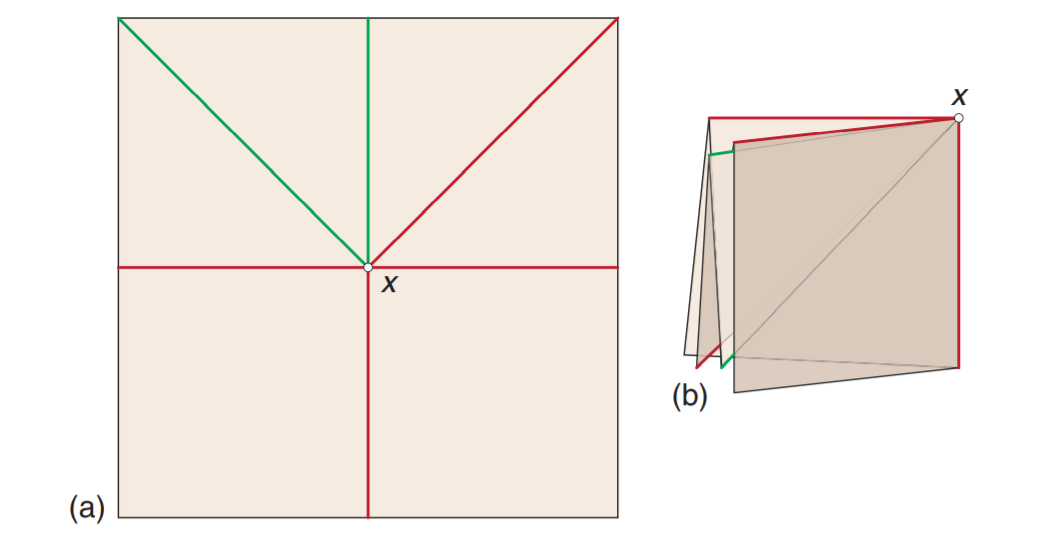
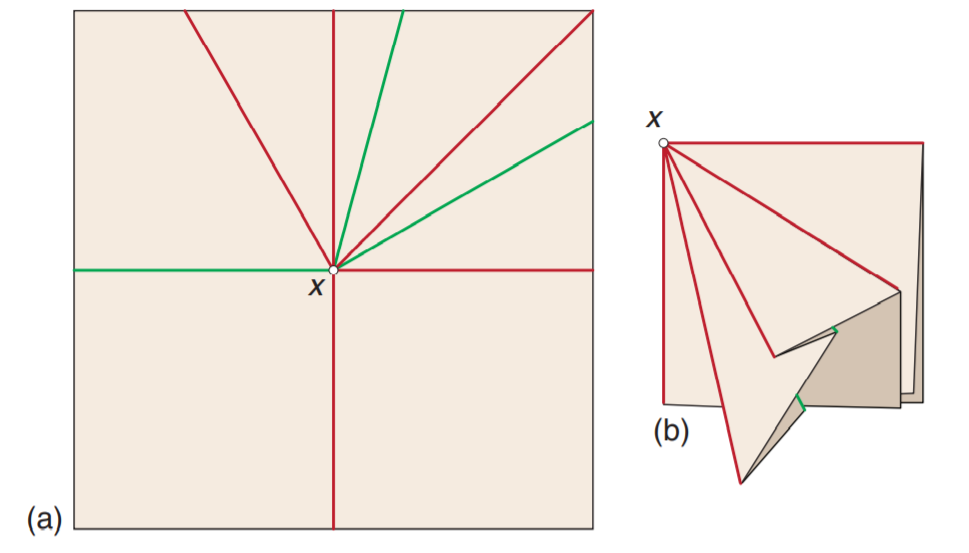
让$M(\text{Mountain})$和$V(\text{Valley})$分别代表平顶点折叠中山折和谷折的数量,则前川定理可以表示为
$M = V +2 \quad \text{or}\quad V = M + 2$
即$|M-V|=2$
$\text{Proof}\;1:$
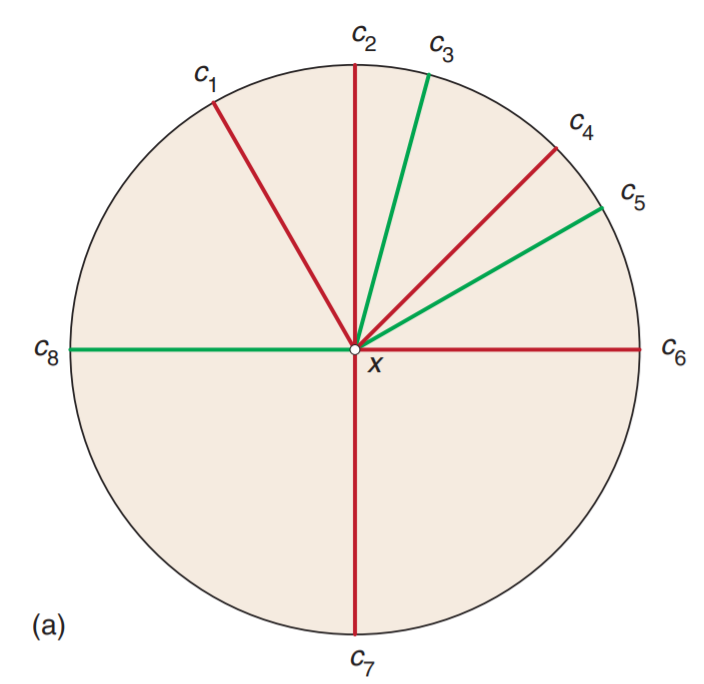
由于我们只关心顶点$x$和周围的折痕,所以可以以$x$为圆心做一个圆$(a)$,按折痕折叠后形成$(b)$
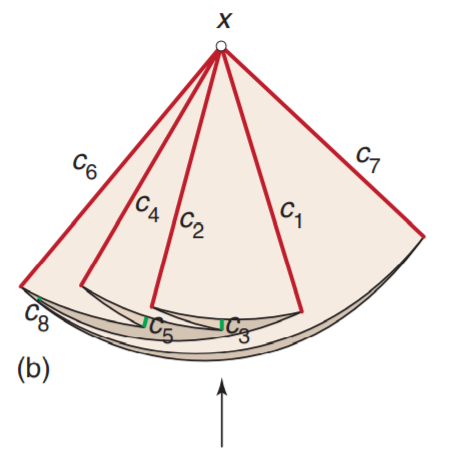
从下往上看向顶点x,可以发现圆环形成了一个闭合回路$(c)$

想象有一个蚂蚁从$p$点出发在这个闭合回路上爬行,遇到山折便逆时针旋转$180^{\circ}$,遇到谷折便顺时针旋转$180^{\circ}$,最后回到原点,方向和开始一样,由于沿着闭合回路走了一周,相当于旋转了$360^{\circ}$度,即
$M · 180^{\circ} +V ·(−180^{\circ}) = 360^{\circ}$
$M − V = 2$
因为纸有两面,如果从另一面看,原来的山折变成了谷折,原来的谷折变成了山折,所以有
$V − M = 2$
这样便证明了前川定理
$\text{Proof}\;2:$
这个证明是由$\text{Jan Siwanowicz}$在他还是个高中生的时候提出的
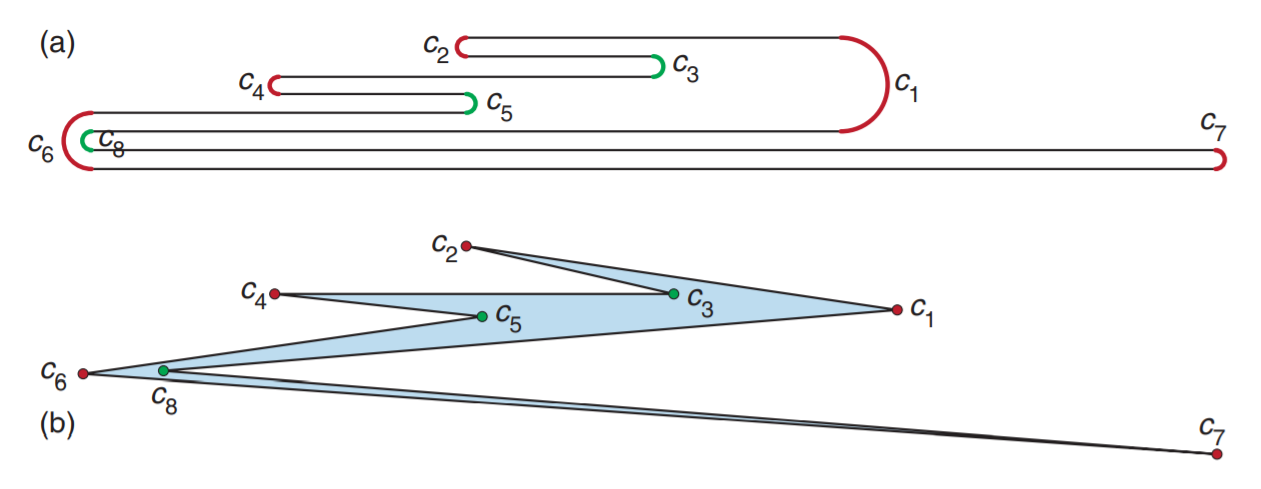
将此前的闭合回路看作一个多边形,把山折看成内角等于$0$,谷折看成内角等于$360^{\circ}$
由多边形内角和定理
$\sum\limits_{i=1}^n\theta_i=(n-2)×180^{\circ}$
推得在这个多边形中,内角和为
$M · 0^{\circ} +V · 360^{\circ}$
所以$V · 360^{\circ} = (M +V-2)180^{\circ}$
$\therefore M = V +2 \quad \text{or}\quad V = M + 2$
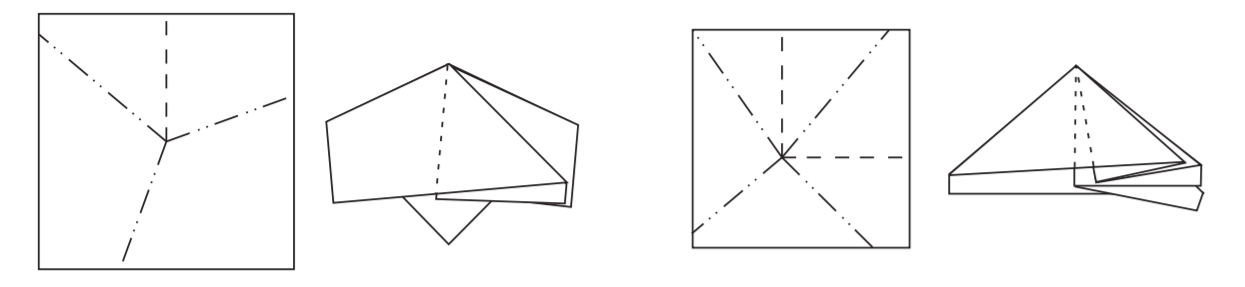
推广:
$M + V = 2(V+1) \quad \text{or} \quad2(V − 1)$
得到偶数定理:单顶点折叠中折痕总数必为偶数,角的总数也必为偶数