大一/web/js

Posted on 2022-08-12

函数

$\rm Javascript$中的函数和$\rm Python$中极其相似

函数表达式

let sayHi = function() {
  alert( "Hello" );
};//可以匿名

console.log(sayHi)//打印出函数的代码

函数表达式可作为参数传递(称为回调函数)

rest参数(形式为’…变量名’)，rest参数只能作为最后一个参数，相当于*args

箭头函数

let func = function(arg1, arg2, ..., argN) {
  return expression;
};
//等价于
let func = (arg1, arg2, ..., argN) => expression;
//若无参数()=>

特性

或运算

寻找第一个真值

1	result = value1 \|\| value2 \|\| value3;

若value1，value2都为null则返回value3(非空)

与运算

寻找第一个假值

// 如果第一个操作数是真值，
// 与运算返回第二个操作数：
alert( 1 && 0 ); // 0
alert( 1 && 5 ); // 5

// 如果第一个操作数是假值，
// 与运算将直接返回它。第二个操作数会被忽略
alert( null && 5 ); // null
alert( 0 && "no matter what" ); // 0

…扩展运算符

相当于python的解包*

模板字符串

反引号``

除了作为普通字符串，还可以用来定义多行字符串，还可以在字符串中加入变量和表达式

正则表达式

let re = new RegExp('ab+c');

// 等价于
let re = /ab+c/;

DOM

文档对象模型，每个 HTML 标签都是一个对象

从而有利于js对HTML元素进行修改

window.onload与$(document).ready()

一个是需要网页全部加载完(包括图片)

第二个只要DOM树加载完就行

Event

Event 对象代表事件的状态，比如事件在其中发生的元素、键盘按键的状态、鼠标的位置、鼠标按钮的状态

事件监听

1	window.addEveantListener(eventType, (event)=>{}, false)

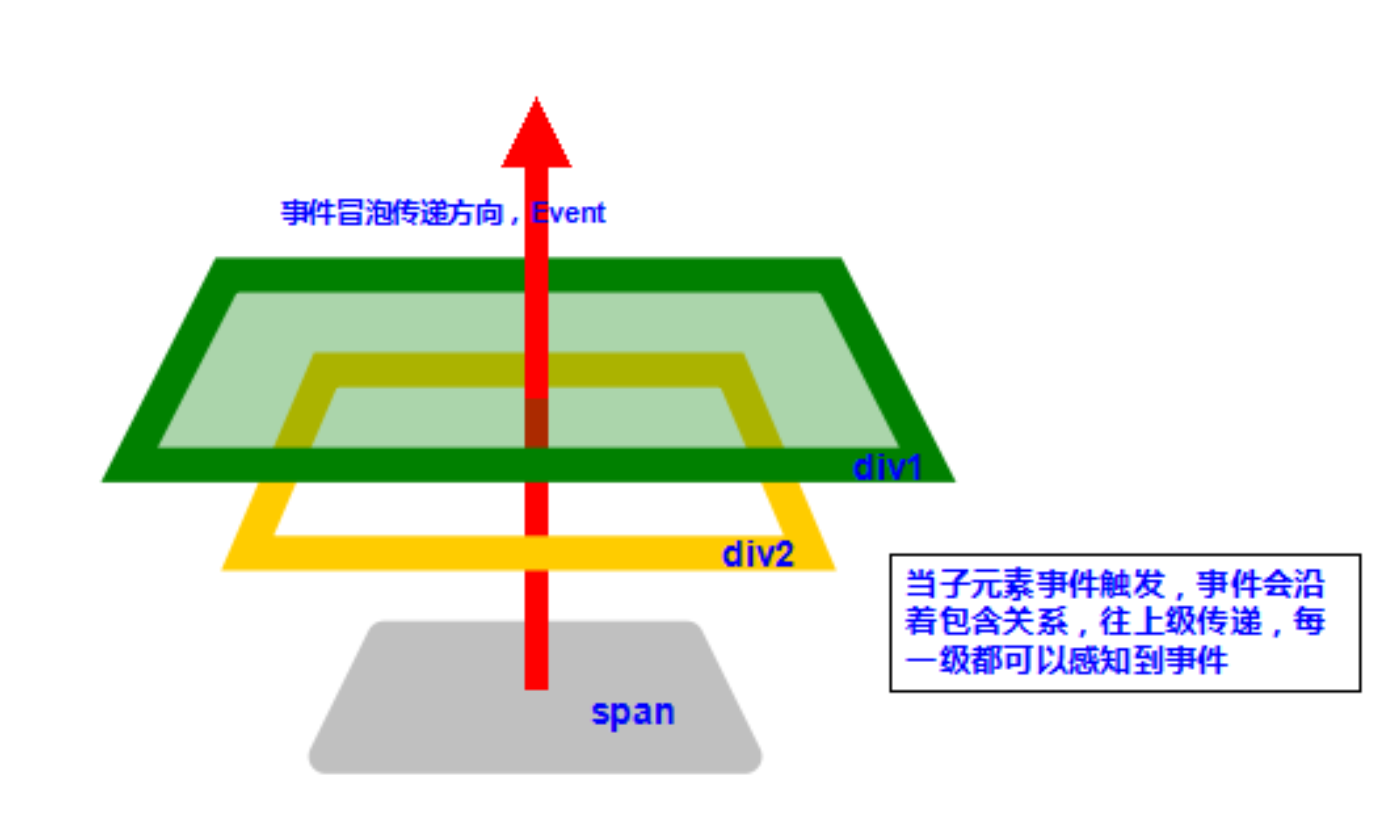
事件由子元素传递到父元素的过程叫做冒泡（false）

事件由父元素传递到子元素的过程叫做事件捕获（ture）

false表示事件冒泡,为true表示事件捕获

事件捕获和事件触发(冒泡)是相反的,也就是说,当用户触发了一个事件的时候,这个事件是从DOM树的最上层开始触发一直到捕获到事件源

属性	描述
altKey	返回当事件被触发时，”ALT” 是否被按下。
button	返回当事件被触发时，哪个鼠标按钮被点击。
clientX	返回当事件被触发时，鼠标指针的水平坐标。
clientY	返回当事件被触发时，鼠标指针的垂直坐标。
ctrlKey	返回当事件被触发时，”CTRL” 键是否被按下。
metaKey	返回当事件被触发时，”meta” 键是否被按下。
relatedTarget	返回与事件的目标节点相关的节点。
screenX	返回当某个事件被触发时，鼠标指针的水平坐标。
screenY	返回当某个事件被触发时，鼠标指针的垂直坐标。
shiftKey	返回当事件被触发时，”SHIFT” 键是否被按下。

`cancelable`	返回布尔值，指示事件是否可拥可取消的默认动作。
`currentTarget`	返回其事件监听器触发该事件的元素。
eventPhase	返回事件传播的当前阶段。
`target`	返回触发此事件的元素（事件的目标节点）。
timeStamp	返回事件生成的日期和时间。
`type`	返回当前 Event 对象表示的事件的名称。
initEvent()	初始化新创建的 Event 对象的属性。
`preventDefault()`	通知浏览器不要执行与事件关联的默认动作。
`stopPropagation()`	不再派发事件，阻止冒泡

target：触发事件的元素。
currentTarget：事件绑定的元素

比如说现在有A和B，A包含B， A监听鼠标点击事件那么当点击B时，target是B，currentTarget是A 也就是说，currentTarget始终是监听事件者，而target是事件的真正发出者

比如有两个div

<div id="div_1">
<div id="div_2">
click here
</div>
</div>

1
2
3

document.getElementById("div_2").addEventListener("click",(event)=>{
    tar=event.target
    tar.style.background="red"

点div_2时

1
2
3

document.getElementById("div_1").addEventListener("click",(event)=>{
    tar=event.target
    tar.style.background="red"

点哪个哪个变红

1
2
3

document.getElementById("div_2").addEventListener("click",(event)=>{
    tar=event.currentTarget
    tar.style.background="red"

始终都是大的都变红

数据传输

跨源读取阻止 (CORB) 是一种浏览器功能，旨在防止攻击者通过欺骗用户的方式获取敏感信息。它通过阻止浏览器向具有不同域的服务器发送请求，并将其响应内容作为 text/html 解析来实现。

例如，假设你有一个页面，其中包含一个带有恶意内容的 iframe。如果你的浏览器没有 CORB 功能，则可能会被攻击者欺骗，将恶意信息发送到服务器，而不知道这是在发生什么。但是，如果你的浏览器具有 CORB 功能，则浏览器会阻止请求，并告诉你发生了什么。

GET – 从指定的资源请求数据。
POST – 向指定的资源提交要被处理的数据。

get 可以直接从地址栏提交

post需要用到相关插件

获取坐标

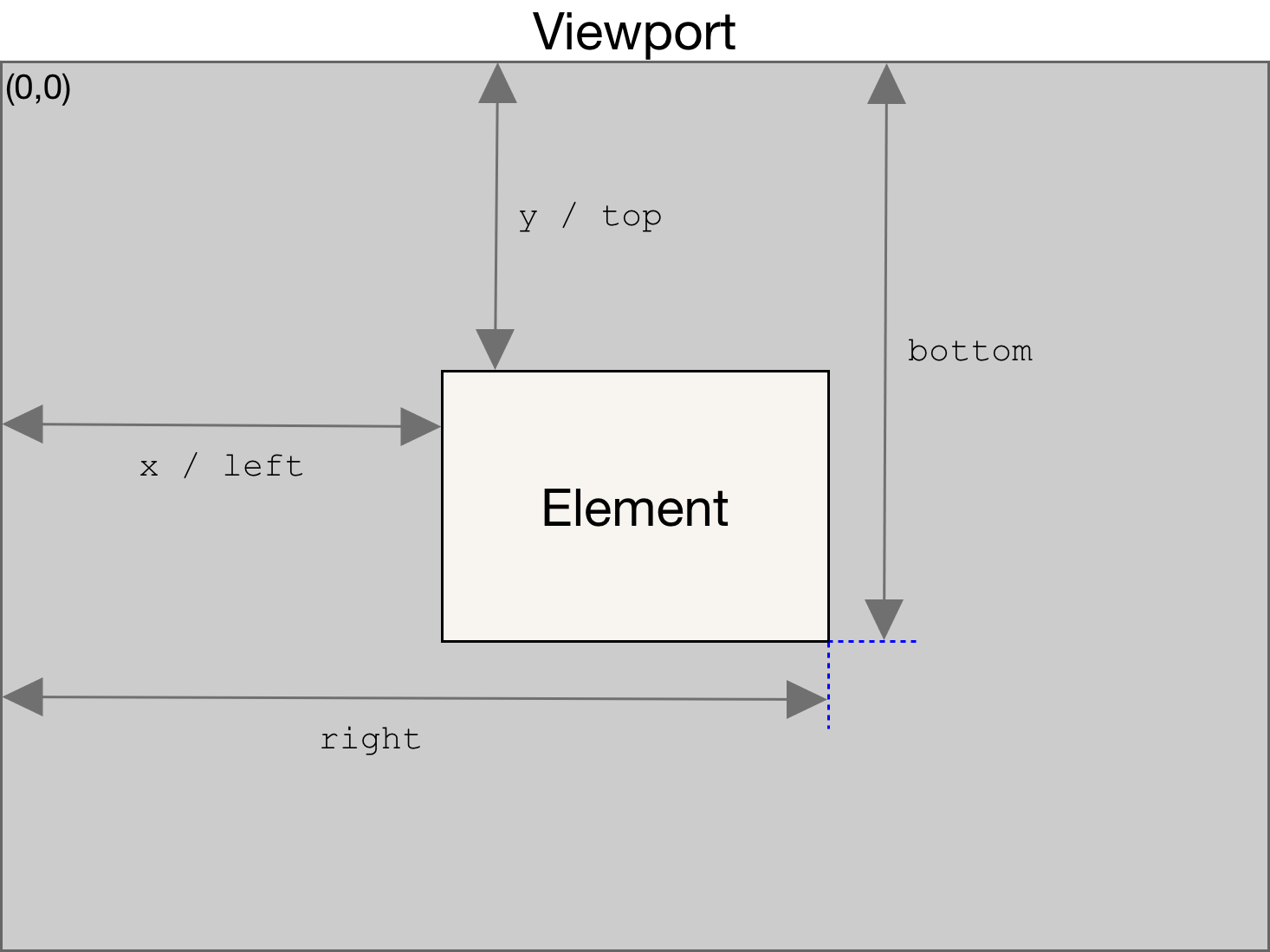
DOMRect object that is the smallest rectangle containing the entire element.

 var rect=element.getBoundingClientRect()
 var x=rect.left//相对于窗口来说
 
window.scrollY滚动了多少
var width = window.innerWidth;
var height = window.innerHeight;
获取当前窗口的长宽
$(ele)[0].offsetHeight
获取高

大一/python/taichi/操作

Posted on 2022-08-10

For

for i,j in field:
	fielf[i,j]=1
    #二维遍历

def func(vx:ti.f32,vy:f64) -> ti.i32#int32

ti.func#只能在ti.kernel
#无需声明类型(inline)

print

$\rm print(arg1,sep=\text{' '},end=\text{'\n'})$

GUI

$\rm gui=ti.GUI(\text{my title},(512,512))$

大一/python/taichi/数据

Posted on 2022-08-10

初始化

1 2	import taichi as ti ti.init(arch=ti.gpu)

修饰

1 2	@ti.kernel#某个函数 #最外层才会并行

数据

cast#i32/i64/f32/f64
b=ti.cast(a,ti.i32)#转换

#大写
a=ti.Vector([0.0,0.0,0.0])
B=ti.Matrix([1.5,1.4],[1.3,1.2])
B[1,0] 
r=ti.Struct(v1=a,v2=0)#结构体

#N-d array(global)
c=ti.field(dtype=ti.f32,shape=(256,256))
#shape=4 -vector
#shape=() [None]
vf=ti.Vector.field(n=3,shape=4)#m每个元素为(3*1)的小向量
#m=2(3*2)

计算

1 2	+=/ti.atomic_add(a,b) #防止数据征用

import taichi as ti
ti.init(ti.gpu)

N=2
vol=ti.Vector.field(2,ti.f32,N)#二维向量
acc=ti.Vector.field(2,ti.f32,N)
pos=ti.Vector.field(2,ti.f32,N)
substepping=10

@ti.kernel
def initialize():
    for i in range(N):
        pos[i]=[ti.random(),ti.random()]
        vol[i]=[ti.random(),ti.random()]

gui=ti.GUI("n body problem",(512,512))
           
while(gui.running):
    # for i in range(substepping):
    gui.circle(pos.to_numpy(),color=0xFFFFFF,radius=2)
    gui.show()

大一/杂/图形学

Posted on 2022-08-07

欧拉方法

显式欧拉方法

$\begin{cases}\vec{v}\left(t_{1}\right)=\vec{v}\left(t_{0}\right)+M^{-1} \vec{F}\left(t_{0}\right)\Delta t \\ \vec{x}\left(t_{1}\right)=\vec{x}\left(t_{0}\right)+\vec{v}\left(t_{0}\right) \Delta t\end{cases}$

用当前的状态计算速度和加速度$(\text{Forward} )$

能量增加，开放的系统

$\int_{t^{[0]}}^{t^{[1]}}\boldsymbol v(t)\text dt=\boldsymbol v(t^{[0]})\Delta t$

隐式欧拉方法

$\vec{v}\left(t_{1}\right)=\lambda(\vec{v}\left(t_{0}\right)+M^{-1} \vec{F}\left(t_{1}\right)\Delta t) \\ \vec{x}\left(t_{1}\right)=\vec{x}\left(t_{0}\right)+\vec{v}\left(t_{1}\right) \Delta t$

用未来的状态去计算速度和加速度再来更新$(\text{Backward} )$

$\int_{t^{[0]}}^{t^{[1]}}\boldsymbol v(t)\text dt=\boldsymbol v(t^{[1]})\Delta t$

中点方法

$\int_{t^{[0]}}^{t^{[1]}}\boldsymbol v(t)\text dt=\boldsymbol v(t^{[0.5]})\Delta t$

二阶准确

半隐式欧拉方法

$\vec{v}\left(t_{1}\right)=\vec{v}\left(t_{0}\right)+M^{-1} \vec{F}\left(t_{0}\right)\Delta t \\ \vec{x}\left(t_{1}\right)=\vec{x}\left(t_{0}\right)+\vec{v}\left(t_{1}\right) \Delta t$

本质上为显式方法

旋转

欧拉角

$\mathbf{R}_{x y z}(\alpha, \beta, \gamma)=\mathbf{R}_{x}(\alpha) \mathbf{R}_{y}(\beta) \mathbf{R}_{z}(\gamma)$

任意旋转都可以分解为绕$x,y,z$三个轴的旋转

顺序非常重要

$\mathbf{R}_{x}(\alpha) \mathbf{R}_{y}(\beta) \mathbf{R}_{z}(\gamma)\ne\mathbf{R}_{x}(\alpha)\mathbf{R}_{z}(\gamma) \mathbf{R}_{y}(\beta)$

飞机滚转（Roll）；飞机俯仰（Pitch）；飞机偏航（Yaw）

罗德里格斯旋转公式

$\mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{array}\right)}_{\mathbf{N}}$

四元数

$q=(q_1, q_ 2, q _3, q _4)=\left(\cos \left(\frac{\theta}{2}\right), \sin \left(\frac{\theta}{2}\right) n_ x, \sin \left(\frac{\theta}{2}\right) n_ y, \sin \left(\frac{\theta}{2}\right)n_ z\right)$

对应于绕$\mathbf{n}$的旋转

$p'=qpq^{-1}$

质点弹簧系统

$f_{a\to b}$为弹簧作用在$a$上的力

能量耗散

引入阻力

$f=-k_d\dot{\boldsymbol x}$

但表示合速度，表示不了弹簧内部的损耗

$f_a=-k_s\frac{\boldsymbol a-\boldsymbol b}{||\boldsymbol a-\boldsymbol b||}(\dot{\boldsymbol a}-\dot{\boldsymbol b})\cdot\frac{\boldsymbol a-\boldsymbol b}{||\boldsymbol a-\boldsymbol b||}$

流体

不可压缩流体

$h_{i}\left(t_{0}+\Delta t\right)=2 h_{i}\left(t_{0}\right)-h_{i}\left(t_{0}-\Delta t\right)+\frac{\Delta t^{2}}{\Delta x^{2} \rho}\left(\left(\frac{h_{i-1}+h_{i}}{2}\right)\left(P_{i-1}-P_{i}\right)+\left(\frac{h_{i+1}+h_{i}}{2}\right)\left(P_{i+1}-P_{i}\right)\right)\\ h_{i}\left(t_{0}+\Delta t\right)=h_{i}\left(t_{0}\right)+\beta\left(h_{i}\left(t_{0}\right)-h_{i}\left(t_{0}-\Delta t\right)\right)+\alpha\left(h_{i+1}\left(t_{0}\right)+h_{i-1}\left(t_{0}\right)-2 h_{i}\left(t_{0}\right)\right)$

有限元

形函数

$\begin{pmatrix}X\\Y\\Z\end{pmatrix}=\sum_{i=0}^{i=3}\begin{pmatrix}X_i\\Y_i\\Z_i\end{pmatrix}\phi_i\left(\mathbf{X}\right) \\ \begin{pmatrix}X-X_0\\Y-Y_0\\Z-Z_0\end{pmatrix}=\begin{pmatrix}\Delta X_1&\Delta X_2&\Delta X_3\\\Delta Y_1&\Delta Y_2&\Delta X_3\\\Delta Z_1&\Delta Z_2&\Delta X_3\end{pmatrix}\begin{pmatrix}\phi_1\left(\mathbf{X}\right)\\\phi_2\left(\mathbf{X}\right)\\\phi_3\left(\mathbf{X}\right)\end{pmatrix}$

所以

$\begin{pmatrix}\phi_1\left(\mathbf{X}\right)\\\phi_2\left(\mathbf{X}\right)\\\phi_3\left(\mathbf{X}\right)\end{pmatrix}=T^{-1}(\mathbf{X}-\mathbf{X}_0)$

齐次坐标

变换

$\mathbf{x}\left(\mathbf{X}\right)=\sum_{i=0}^{i=3}\mathbf{x}_{i}\left(t\right){\phi_{i}\left(\mathbf{X}\right)}\\ \mathbf{x}\left(\mathbf{X}\right)=\begin{pmatrix}\phi_0\mathbf{I}&\phi_1\mathbf{I}&\phi_2\mathbf{I}&\phi_3\mathbf{I}\end{pmatrix}\begin{pmatrix}\mathbf{x}_0\\\mathbf{x}_1\\\mathbf{x}_2\\\mathbf{x}_3\end{pmatrix}$

求动能

$\mathbf{v}\left(\mathbf{X}\right)=\dot{\mathbf{x}}\left(\mathbf{X}\right)=\mathbf{N}\left(\mathbf{X}\right)\dot{\mathbf{q}}\\ \frac12\int_{\Omega}\rho\mathbf{v}^T\mathbf{v}d\Omega =\frac12\int_{\Omega}\rho\left(\dot{\mathbf{q}}^T\mathrm{N}\left(\mathbf{X}\right)^T\mathrm{N}\left(\mathbf{X}\right)\dot{\mathbf{q}}\right)d\Omega$

重组

$\frac12\dot{\mathbf{q}}^T\left(\int_{\Omega}\rho\mathrm{N}\left(\mathbf{X}\right)^T\mathrm{N}\left(\mathbf{X}\right)d\Omega\right)\dot{\mathbf{q}}=\frac12\dot{\mathbf{q}}^T\mathbf{M}_0\dot{\mathbf{q}}$

$\mathbf{M}_0$为单元的质量矩阵

$6\rho\cdot\boldsymbol{vol}\cdot\int_0^1\int_0^{1-\phi_1}\int_0^{1-\phi_1-\phi_2}\left(\phi_r\phi_s\right)d\phi_3d\phi_2d\phi_1$

大一/线性代数/向量

Posted on 2022-08-07

向量

$\rm vector$ 表示

$\vec{a}/\mathbf{a}$

$||\vec{a}||$为向量的长度

在直角坐标系中

$||\vec{a}||=\sqrt{x^2+y^2}\\ 单位向量\hat{a}=\vec{a}/||\vec{a}||$

两向量之间的夹角为$0\le\left \langle \alpha,\beta \right \rangle \le \pi$

点乘

$\rm Dot\;Product$

$\vec{a} \cdot \vec{b}=\|\vec{a}\|\|\vec{b}\| \cos \theta =x_1x_2+y_1y_2 \\ \cos \theta=\frac{\vec{a} \cdot \vec{b}}{\|\vec{a}\|\|\vec{b}\|}\\ \theta=\arccos (\hat{a}\cdot\hat{b})$

矩阵

$\vec{a} \cdot \vec{b}=a^Tb$

运算性质

$交换律：\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a} \\ 分配律：\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} \\ (k \vec{a}) \cdot \vec{b}=\vec{a} \cdot(k \vec{b})=k(\vec{a} \cdot \vec{b})$

叉乘

$\rm Cross \;Product$

$||\vec{a}\times\vec{b}||=||\vec{a}||||\vec{b}||\sin\theta$

运算性质

$\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}\\ \vec{k}=\vec{i}\times \vec{j}$ $\begin{array}{l}\vec{a} \times \vec{b}&=\left(\begin{array}{c} y_{a} z_{b}-y_{b} z_{a} \\ z_{a} x_{b}-x_{a} z_{b} \\ x_{a} y_{b}-y_{a} x_{b} \end{array}\right)=\begin{vmatrix} i& j & k\\ x_a &y_a &z_a \\ x_b & y_b &z_b \end{vmatrix}\\ &=\begin{bmatrix} 0& -z_a & y_a\\ z_a &0 &-x_a \\ y_a & x_a &0 \end{bmatrix}\begin{bmatrix} x_b\\ y_b \\ z_b \end{bmatrix}=[a]_\times b\end{array}\\ [a]_\times+[a]_\times^\text T=0$

混合积

$[\vec{a}\;\vec{b}\; \vec c]=\vec{a}\times\vec{b}\cdot \vec c\\ =\begin{vmatrix} x_c& y_c & z_c\\ x_a &y_a &z_a \\ x_b & y_b &z_b \end{vmatrix}$

根据Levi-Civita

$\vec{a}\times\vec{b}\cdot \vec c=\vec{b}\times\vec{c}\cdot \vec a=\vec{c}\times\vec{a}\cdot \vec b$

范数

$||\vec{x}||_p=\sqrt[p]{\sum_{i=1}^n|x_i|}$ $\|x\|_{1}=\left|x_{1}\right|+\cdots+\left|x_{n}\right| \\ \|x\|_{2}=\sqrt{\left|x_{1}\right|^{2}+\cdots+\left|x_{n}\right|^{2}}=\sqrt{x^{H} x} \\ \|x\|_{\infty}= \underset{1 \leq i \leq n}\max|x_{i}|$

表示

根据三角形法则，对于任何一个向量

都可以分解为两个基向量的线性组合

$\vec{OP}=x\boldsymbol{i}+y\boldsymbol{j}$

所有线性组合构成集合$\text{span}(\boldsymbol{i},\boldsymbol{j})$，称为张成空间

这就是向量的坐标表示法

$\vec{OP}=\left(\begin{array}l x\\y\end{array}\right)\\ \boldsymbol{i}=\left(\begin{array}l 1\\0\end{array}\right),\boldsymbol{j}=\left(\begin{array}l 0\\1\end{array}\right)$

直线的向量方程

对于直线，有如下关系

$\vec{OR}=\vec{OA}+t\vec{AR}\quad(t\in \mathbf{R})$

其中非零向量$\vec{AR}$为该直线的方向向量

写成坐标形式，可得

$\left(\begin{array}l x\\y\end{array}\right)=\left(\begin{array}l x_0\\y_0\end{array}\right)+t\left(\begin{array}l v_1\\v_2\end{array}\right)$

导数

求导的本质只是把标量求导的结果排列起来，至于是按行排列还是按列排列都是可以的

最基本的求导布局有两个：

分子布局(numerator layout)和分母布局(denominator layout )

机器学习主要为分子布局

分子布局：分子为列向量，分母为行向量

$\mathbf{x}=\begin{bmatrix}x_1\\x_2\\ \vdots \\x_n\end{bmatrix} \\\frac{\partial y}{\partial \mathbf{x}}=\begin{bmatrix}\frac{\partial y}{\partial x_1} \frac{\partial y}{\partial x_2} \cdots \frac{\partial y}{\partial x_n} \end{bmatrix}$

方向导数，定义的$\rm shape$，例

$\frac{\partial}{\partial \mathbf{x}}(x_1^2+2x_2^2)=[2x_1,4x_2]$

求导运算是线性算子

$\mathbf{y}=\left[\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \end{array}\right] \quad \frac{\partial \mathbf{y}}{\partial x}=\left[\begin{array}{c} \frac{\partial y_{1}}{\partial x} \\ \frac{\partial y_{2}}{\partial x} \\ \vdots \\ \frac{\partial y_{m}}{\partial x} \end{array}\right]$

雅可比矩阵

$\text{jacobi matrix} \\\frac{\partial \mathbf{y}}{\partial \mathbf{x}}=\left[\begin{array}{c} \frac{\partial y_{1}}{\partial \mathbf{x}} \\ \frac{\partial y_{2}}{\partial \mathbf{x}} \\ \vdots \\ \frac{\partial y_{m}}{\partial \mathbf{x}} \end{array}\right]=\left[\begin{array}{c} \frac{\partial y_{1}}{\partial x_{1}}, \frac{\partial y_{1}}{\partial x_{2}}, \ldots, \frac{\partial y_{1}}{\partial x_{n}} \\ \frac{\partial y_{2}}{\partial x_{1}}, \frac{\partial y_{2}}{\partial x_{2}}, \ldots, \frac{\partial y_{2}}{\partial x_{n}} \\ \vdots \\ \frac{\partial y_{m}}{\partial x_{1}}, \frac{\partial y_{m}}{\partial x_{2}}, \ldots, \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right]$

线性回归

$x , w \in \mathbf{R }^ { n } , y \in \mathbf{R } \\ z = (\left \langle \mathbf{x} ,\mathbf{w} \right \rangle - y ) ^ { 2 }$ $\begin{aligned}\frac{\partial z}{\partial \mathbf{w}}\end{aligned}=2(\left \langle \mathbf{x} ,\mathbf{w} \right \rangle - y )\mathbf{w}^{\rm T}$

求导

采用分子布局

$\frac{\partial A x}{\partial x}=A\\ \frac{\partial A x}{\partial x^{T}}=A^{T} \\ \frac{\partial x^{T} A}{\partial x}=A^{T}$

ca965b6eb9595c5542db8fa385d9d58a

场论

$\vec{F}(x,y,z)=f_x(x,y,z)\mathbf{i}+f_y(x,y,z)\mathbf{j}+f_z(x,y,z)\mathbf{k}$

梯度

$(x',y')=F(x,y)$

向量场里每个点赋予一个向量

$\nabla=\begin{bmatrix}\frac{\partial }{\partial x_1} \frac{\partial}{\partial x_2} \cdots \frac{\partial }{\partial x_n}\end{bmatrix}$

散度

$\text{div}F(x,y)=\nabla\cdot F$

描述净流量，若流入大于流出则为负

$(x,y)$点生成的流量

例如对于不可压缩的流体

$\text{div}V=0$

旋度

$\text{curl}F(x,y) =\nabla\times F$

$\begin{array}{l}\nabla\cdot F= {\left[\begin{array}{c} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \end{array}\right] \cdot\left[\begin{array}{c} \mathbf{F}_{x} \\ \mathbf{F}_{y} \end{array}\right]=\frac{\partial F_{x}}{\partial x}+\frac{\partial F_{y}}{\partial y}} \\ {\nabla\times F=\left[\begin{array}{c} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \end{array}\right] \times\left[\begin{array}{c} \mathbf{F}_x \\ \mathbf{F}_{y} \end{array}\right]=\frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y}} \end{array}$

大一/python/manim/updater/updater

Posted on 2022-08-06

updater(迭代，更新器)

语法：$\rm mobject.add_updater(anim)$

anim 为更新的规则

1
2
3

def anim(obj):
    obj.next_to(obj_2,RIGHT)
    #将obj放在obj_2的右侧

可以合二为一

1 2	mobject.add_updater(lambda m:m.next_to(obj,RIGHT)) #使用匿名函数

删除updater:

$\rm case\;1:mobject.remove\_updater(anim)\\移除某个updater\\ case\;2:mobject.clear\_updater()\\移除全部updater$

UpdateFromFunc

直接更新，不用添加updater：

self.play(
    UpdateFromFunc(
        obj,
        lambda m:m.next_to(obj_2,RIGHT)
    )
)

拓展

UpdateFromAlphaFunc

传入一个含有参数==$\rm alpha$==的函数

def move(obj,alpha):
    obj.shift(alpha*RIGHT)
    obj.rotate(alpha*TAU)#TAU=2*PI
   
self.play(UpdateFromAlphaFunc(t,move))

不太推荐使用此方法

dt

根据时间进行迭代

def anim(obj,dt):
            obj.shift(dt*RIGHT)
        
mobject.add_updater(anim)
self.wait(time)#基于时间进行更新

ValueTracker

初始化设为$-1$

$\rm t=ValueTracker(-1)$

接着可以生成目标

1 2	self.play(t.set_value,1,rate_func=,run_time=3) #目标值为1

x1=ValueTracker(0)
        n2=Tex("0")
        n2.add_updater(lambda t:t.become(Tex(str(round(x1.get_value(),1)))))
        self.play(ShowCreation(n2))
        self.play(x1.set_value,1,rate_func=smooth,run_time=3)

大一/线性代数/矩阵与行列式

Posted on 2022-08-04

行列式

定义

由小到大为标准次序，$p_1p_2\cdots p_n$为排列，则比$p_i$大且排在其前的元素有$t_i$个，就说这个元素的逆序数是$t_i$

排列逆序数

$t=\sum_{i=1}^nt_i$

则行列式

$D=\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\cdots&\cdots&\cdots&\cdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}$ $D=\sum(-1)^ta_{1p_1}a_{2p_2}\cdots a_{np_n}\quad(n!项)$

余子式

去掉$i$行$j$列得到的子行列式$M_{ij}$

代数余子式

$A_{ij}=(-1)^{i+j}M_{ij}$

则行列式可以按$i$行展开

$D=\sum_j^na_{ij}A_{ij}$

性质

对换行列式的两行或者两列(不需相邻)行列式变号
行列式与它的转置行列式相等
行列式中的某一行/列中所有元素乘以同一数$k$等于用数$k$乘以行列式
行列式中如果有两行/列成比例则行列式为零
把某一行/列的各元素同乘一个数然后加到另一行/列上行列式不变

范德蒙德行列式

$D_n=\begin{vmatrix}1&1&\ldots&1\\x_1&x_2&\ldots&x_n\\\vdots&\vdots&&\vdots\\x_1^{n-1}&x_2^{n-1}&\ldots&x_n^{n-1}\end{vmatrix}=\prod_{1\le i<j\le n}(x_j-x_i)$

爪形

$\begin{vmatrix}a_0&&1&&1&\cdots&1\\1&&a_1\\1&&&a_2&&\\\vdots&&&&\ddots&\\1&&&&&a_n\end{vmatrix}$

用对角线去消第一行/列

三对角线行列式递推求解

$D_n=aD_{n-1}-bcD_{n-2}$

观察并灵活利用拆行求和换序加边升阶等方法

$A(m\times n),B(n\times m)\\ \lambda^{n}\mathrm{det}(\lambda I_{m}+AB)=\lambda^{m}\mathrm{det}(\lambda I_{n}+BA)$

运算

$AB\ne BA\\ |AB|=|A||B|=|BA|\\ (AB)^{-1}=B^{-1}A^{-1}$ $|A^{-1}|=\frac1{|A|}\\ |A^*|=|A|^{n-1}$

矩阵

矩形的数组，如

$A=\left[\begin{array}{l} a_{11} &a_{12}&a_{13}\\a_{21} &a_{22}&a_{23}\end{array}\right] =\left[\begin{array}{l} 1 &2&3\\4&5&6\end{array}\right]$

是一个$2\times3$的矩阵$A=(a_{ij})$其中$i=1,2;j=1,2,3$

矩阵中第$i$行第$j$列的元素表示为$a_{ij}$(大写矩阵，小写元素)

向量

向量是一维数组($1D$ ,如只有一行或一列)，如

$x=\left(\begin{array}l 1\\2\\3\end{array}\right)$

把长度为$n$的向量称为$n$向量，通常用小写字母来表示向量

$x_i$表示向量中第$i$个元素

向量的标准形式为列向量($n\times1$)

$x^{\text T}=(1,2,3)$

特殊的矩阵

零矩阵

所有元素均为$0$的矩阵，矩阵大小需要从上下文中推测

方阵

方阵为$n\times n$矩阵

对角矩阵

对角线($\text {diagnoal}$)，其中对于任意$i\ne j,a_{ij}=0$，故只需列出对角线上的元素就可以表示出这个矩阵

$\Lambda =\text{diag}(a_{11},a_{22},\cdots,a_{nn})=\begin{bmatrix} a_{11} &0& \cdots & 0\\ 0 &a_{22}&\cdots&0 \\ \vdots &\vdots& \ddots & \vdots\\ 0 & 0&\cdots & a_{nn} \end{bmatrix}$ $\Lambda^k=\text{diag}(a_{11}^k,a_{22}^k,\cdots,a_{nn}^k)$

单位矩阵

$I_n=\text{diag}(1,1,\cdots,1)$

逆矩阵

伴随矩阵

$A^{*}=\begin{pmatrix}A_{\mathrm{ll}}&A_{21}&\cdots&A_{n1}\\A_{\mathrm{l2}}&A_{22}&\cdots&A_{n2}\\\cdots&\cdots&\cdots&\cdots\\A_{\mathrm{ln}}&A_{2n}&\cdots&A_{nn}\end{pmatrix}$

故

$A^{-1}=\frac{A^*}{|A|}\\ (A^{-1})^T=(A^T)^{-1}$ $A=P\Lambda P^{-1}\\ \varphi(A)=P\varphi(\Lambda) P^{-1}$

二阶矩阵

$\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}=\frac1{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}$

三对角矩阵

对$|i-j|>1,a_{ij}=0$，即矩阵中不为$0$的项只出现在对角线或上下，$i-j$相当于偏移量，类似八皇后问题

上三角矩阵

若$i>j,a_{ij}=0$，其对角线以下的元素为$0$

$U=\left[\begin{array}{ccccc} u_{11} & u_{12} & u_{13} & \cdots & u_{1n} \\ & u_{22} & u_{23} & \cdots & u_{2n} \\ & & \ddots & \ddots & \vdots \\ & & & \ddots & u_{n-1}n \\ & & & & u_{nn} \end{array}\right]$

同理下三角矩阵$L$对角线以上的元素为$0$

若非零项均为$1$，则为单位三角矩阵

$|U|=|L|=\prod_iu_{ii}$

排列矩阵

每行每列只有一个1，其余都为0，可以重新排列向量中的元素

$P=\begin{bmatrix}1&0&0\\0&0&1\\0&1&0\end{bmatrix}$

对称矩阵

若矩阵$A$满足$A=A^{\text T}$，则矩阵的元素关于对角线对称

$\begin{bmatrix}1&2&3\\2&4&5\\3&5&6\end{bmatrix}$

性质$a{ij}=a{ji}$

反对称$a{ij}=-a{ji}$

正交矩阵

$A^T=A^{-1}\\ AA^T=I$ $1=\text{det}(I)=\text{det}(A^TA)=\text{det}(A)^2$

分块矩阵

对角线

$\begin{vmatrix}A&B\\0&D\end{vmatrix}=\left|A\right|\left|D\right|$ $\begin{bmatrix}A&0\\C&D\end{bmatrix}^{-1}=\begin{bmatrix}A^{-1}&0\\-D^{-1}CA^{-1}&D^{-1}\end{bmatrix}$ $\begin{bmatrix}A&B\\0&D\end{bmatrix}^{-1}=\begin{bmatrix}A^{-1}&-A^{-1}BD^{-1}\\0&D^{-1}\end{bmatrix}$ $C=\begin{pmatrix}A&O\\O&B\end{pmatrix}\quad\text{,则 rank(C)}=\mathrm{rank(A)+rank(B)}$

矩阵的基本操作

加法

若矩阵$A,B$大小相同，则$C=A+B$为相同大小

$c_{ij}=a_{ij}+b_{ij}$

数乘

$\lambda A=(\lambda a_{ij})$

$\lambda$称为矩阵的一个标量倍数，矩阵的负为$-A(\lambda=-1)$

故减法$A-B=A+(-B)$

乘法

给定两个相容的矩阵$A,B(A的列数=B的行数)$

设$A$为$m\times p$的矩阵，$B$为$p\times n$的矩阵

则 $C=AB$为$m\times n$的矩阵

$c_{ij}=\sum_{k=1}^pa_{ik}b_{kj}(i=1,\cdots,m;j=1,\cdots,n)$

矩阵乘法满足结合律，分配律

$A(BC)=(AB)C\\ A(\lambda B+\mu C)=\lambda AB+\mu A C\\ A(\lambda B)=\lambda(AB)\\ P^n=(P^{n-1})P$

==$A,B,C$必须是相容的==

意义

对于方阵

$M=\begin{bmatrix}a&b\\c&d\end{bmatrix}\\ M\begin{bmatrix}1\\0\end{bmatrix}=M\boldsymbol{i}=\begin{bmatrix}a\\c\end{bmatrix}\\ M\begin{bmatrix}0\\1\end{bmatrix}=M\boldsymbol{j}=\begin{bmatrix}b\\d\end{bmatrix}$

而有又有向量的分解不难看出

$\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=x\left[\begin{array}{l} a \\ c \end{array}\right]+y\left[\begin{array}{l} b \\ d \end{array}\right]=\left[\begin{array}{c} a x+b y \\ c x+d y \end{array}\right]$

变换

从而很容易理解旋转矩阵

$\mathbf{R}_{\theta}=\left[\begin{array}{l} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$

其中旋转矩阵为正交矩阵

对于转轴$u$

$Ru=u \\(R-R^T)\vec u=0\\ \vec u'\times \vec u=0$ $||R\vec x||=||\vec x||$

对于直线

$M\vec{OR}=M\vec{OA}+tM\vec{AR}$

如果$M\vec{AR}=0$成立，则变化将直线变为一个点

若两个变换后的基向量共线则该变换结果为一维空间(线)

对于变换

$M=\begin{bmatrix}1&0\\0&0\end{bmatrix}\\$

x0=1
y0=1
v1=0
v2=1
t0=-3
t1=1
T=np.linspace(t0,t1,100)
X=x0+v1*T
Y=y0+v2*T
M=np.array([[1,0],[0,0]])
L=np.matmul(M,np.array([X,Y]))

fig=go.Figure()
fig.add_trace(go.Scatter(x=X,y=Y,name=f'原直线'))  
fig.add_trace(go.Scatter(x=L[0],y=L[1],name=f'变换后'))  
fig.update_layout(title='线性变换',
                    xaxis_title='x',yaxis_title='y',xaxis_range=[0,2],yaxis_range=[-3,3])

将直线变化为了一个点，整个平面变换成了$y=0$

一般的，如果一个条直线上的任意$2$个不同的点经过变换后重合

则该变换为不可逆矩阵

缩放

对每个分量乘上比例因子

$P=\begin{bmatrix}s_x&0&0\\0&s_y&0\\0&0&s_z \end{bmatrix}$

转置

交换$A$行和列获得的矩阵为$A$的转置$A^{\text T}$(第几行变为第几列)

$A=\left[\begin{array}{l} 1 &2&3\\4&5&6\end{array}\right] \\ A^{\text T}=\left[\begin{array}l 1&4\\2&5\\3&6\end{array}\right]$ $(A+B)^T=A^T+B^T\\ (\lambda A)^T=\lambda A^T$

观察矩阵的形状

$n\times m=(n\times p)(p\times m)\\ (AB)^{\text T}=B^{\text T}A^{\text T}$

逆

定义

$A^{-1}A=AA^{-1}=I_n$

若没有逆矩阵则称为奇异的

由共线和或叉乘得

$S=\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad-bc$

若面积为$0$则为奇异矩阵

$S_1\to S_2\to S_3 \Rightarrow\\ S_3\to S_2\to S_1\\ (MN)^{-1}=N^{-1}M^{-1}$

简单情况下，对基向量进行研究，通过初等变换矩阵的乘积来得到逆矩阵

一般情况

对线性方程组$Mx=\alpha$，得

$x=\alpha M^{-1}$

对$M=\begin{bmatrix}a&b\c&d\end{bmatrix}$

$MM^{-1}=\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}u&v\\s&t\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}$ $\det M\ne0\\ \Rightarrow M^{-1}=\begin{bmatrix}\frac d{ad-bc}&\frac {-b}{ad-bc}\\\frac {-c}{ad-bc}&\frac a{ad-bc}\end{bmatrix}$

性质

范数

$\rm frobennius$范数

$||A||_{\text{Frob}}=\left[\sum_{ij}a_{ij}^2\right]^{\frac12}$

特征向量

$Ax=\lambda x(x\ne\vec{0})$

表示变换$A$对于$x$构成的张成空间没有影响，$\lambda$称为特征值

例如三维旋转矩阵的特征向量和旋转轴共线并且特征值为$1$

对称矩阵总可以找到特征向量

$\begin{bmatrix}a&b\\c&d\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}=\lambda\begin{bmatrix}x\\y\end{bmatrix}= \begin{bmatrix}\lambda&0\\0&\lambda\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}\\ \begin{bmatrix}a-\lambda&b\\c&d-\lambda\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}=B\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}$ $\Rightarrow A-\lambda I=0$

若$\det A\ne 0$，$x=0$舍去

$\det A= 0$，则空间压缩成一条线

总有一个向量经过变换后得到零向量

解出特征值后可以解出特征向量(可能有很多如缩放)

$\lambda_{\pm}=\frac{T}{2} \pm \sqrt{(T / 2)^{2}-D}\\ T= \text{trace}\\ D=\text{det}$

特征基

利用特征向量可以将矩阵乘法转化为数乘

若将基向量变换为$2$个不共线的特征向量来表示

则有非常好的性质

$M^n=\lambda^n$

再转换回去即可得到结果

应用

$\text E[g(X)]=\sum_xg(x)\cdot\Pr\{X=x\}$

对于一个决策行为，定义收益函数$q(d,h)$

$d_i\in\{\text {act}\;1,\text {act}\;2,\cdots,\text {act}\;n\}$

对于每一种策略，在某个随机变量的影响下都有相应的概率获得不同的收益
| $h$ | $h_1$ | $h_2$ | $h_3$ |
| :——: | :—-: | :—-: | :—-: |
| $p(h)$ | $p_1$ | $p_2$ | $p_3$ |

对于每一种决定$d$

$\overline{q}=\sum_iq(d,h_i)p_i$

写成矩阵形式

$(p_1,p_2,p_3)\left.\underbrace {\begin{pmatrix} q_{11}&q_{12} & q_{13}\\ q_{21} & q_{22} & q_{23}\\ q_{31} &q_{32} &q_{33} \end{pmatrix}}_{d_i}\right\}h_i=(R(d_1),R(d_2),R(d_3))$

决策树

马尔可夫链

$\left(\begin{array}{l}p_1^{(n+1)}\\p_2^{(n+1)}\end{array}\right )=\left(\begin{array}{l}p_{11}& p_{21}\\p_{12}& p_{22}\end{array}\right )\left(\begin{array}{l}p_1^{(n)}\\p_2^{(n)}\end{array}\right )$

其中

$P (X_{n+1}|X=j)=p_1^{(n)}P(X_{n+1}=j|X_n=1)+p_2^{(n)}P(X_{n+1}=j|X_n=2)\\ p_{ij}=P(X_{n+1}=j|X_n=i)$

你们将$p_{ij}$称为转移概率

$P=\left(\begin{array}{l}p_{11}& p_{21}\\p_{12}& p_{22}\end{array}\right )$

称为状态转移矩阵，$(p_1^{(n)},p_2^{(n)})$这样的行向量称为该瓦尔科夫链在时刻$n$的分布

再乘上收益矩阵即可得到两种决策的收益

考虑短期过程，观察平均收益

$q_n(d)=\sum_{k=0}^nq(d,k)$

对于长期过程，有平稳分布

$w=wP\\ w=(w_1,w_2,\cdots),\sum_{i=1}^nw_i=1$

类比不动点，可以使用特征向量得到

$w=\left(\begin{array}{l}p_{11}& p_{21}\\p_{12}& p_{22}\end{array}\right )^nw_0$

大一/高数/函数

Posted on 2022-08-03

基本概念

例：$f(x)=x^2$

定义了一个函数 $f$ ，法则为将一个数转变为它的平方

未指定，故定义域为$\mathbf{R }$(实数集)

意义：$f(2)=4$，通过法则$f$将数字$2$转变为$4$

By the way, $f$ is the transformation rule, while $f(x)$ is the result of applying the transformation rule to the variable $x$. So it’s technically not correct to say “$f(x)$ is a function”; it should be “$f$ is a function.”

区间

$[a, b) \quad\{x: a \leq x<b\}$

$(−8, 13]\backslash \{2\}(\text{not including 2})$

函数

基本初等函数

常函数，幂函数，三角函数，反三角函数，对数函数，指数函数

初等函数是由基本初等函数经过==有限次==复合形成的能用一个式子表示的函数

反三角函数

$x\in[-1,1],y\in\left[-\frac\pi2,\frac\pi2\right]\\ \frac{\text{d}}{\text{d}x}\arcsin x=\frac1{\sqrt{1-x^2}}$

$x\in[-1,1],y\in\left[0,\pi\right]$

重要关系

$\sin\left(\frac\pi2-x\right)=\cos x=t \\ \arcsin x+\arccos x=\frac\pi2$

$x\in\mathbf{R},y\in\left(-\frac\pi2,\frac\pi2\right)$ $\arctan A-\arctan B=\arctan \frac{A-B}{1+A B}$ $A=\tan \alpha \Leftrightarrow \alpha=k\pi+ \arctan A$

例

$f(x)=\cot x(x\in(\pi,2\pi))\\ f_{\text{std}}=\cot(x-\pi),x-\pi=\text{arccot}(x-\pi)\\ f^{-1}(x)=\pi+\text{arccot}(x)$

双曲函数

$\sinh x=\frac{e^x-e^{-x}}2\\ \cosh x=\frac{e^x+e^{-x}}2$ $\cosh^2 x - \sinh^2 x = 1\\ \sinh\left(x+y\right) = \sinh x \cosh y + \cosh x \sinh y\\ \cosh\left(x+y\right) = \cosh x \cosh y + \sinh x \sinh y$

$\sinh^{-1} x = \ln\left(x + \sqrt{x^2 + 1}\right) \\ \cosh^{-1} x = \ln\left(x + \sqrt{x^2 - 1}\right) \\$

函数的极限

$\varepsilon-\delta$定义

$\forall \varepsilon>0$，$\exists \delta>0$，使得$x\in(a-\delta,a+\delta)$时，$|f(x)-A|<\varepsilon$恒成立，但存在$f(a)$无定义，故$0<|x-a|<\delta$

记作：

$\lim_{x\to a}f(x)=A$

去心$\delta$邻域

$\mathring{U}(a,\delta)=\{x|0<|x-a|<\delta,\delta>0\}$

右$\delta$邻域

$\mathring{U}^+(a,\delta)=\{x|0<x-a<\delta\}=(a,a+\delta)$

左右极限

若对$\forall \varepsilon>0$，$\exists \delta>0$，当$x\in\mathring{U}^+(a,\delta)$时恒有${|f(a)-A|<\varepsilon}$

就称$A$为函数$f(x)$在$a$处的右极限，记为

$\lim_{x\to a^+}f(x)=A$

定理

$\lim_{x\to a}f(x)存在\Leftrightarrow\lim_{x\to a^-}f(x)和\lim_{x\to a^+}f(x)\\分别存在且相等$

无穷

设$f(x)$在$|x|>M,M>0$时有定义，$A$为某一常数，若对任意$\varepsilon>$0，都$\exists X>0$使得当$ |x|>X$时

$|f(x)-A|<\varepsilon$

那么就称$A$为函数$f(x)$当$x\to \infty$的极限

$\lim_{x\to \infty}f(x)=A/f(x)\to A(当x\to \infty)$

同理正无穷去掉绝对值

性质

有界性

设$f(x)$在区间$X$上有定义，且对任意$x\in X$，存在$M$使得

$|f(x)|\le M$

就称$f(x)$在$X$上有界

同理若

$f(x)\le K_1$

则称$f(x)$在X上有上界，其中$K_1$为$f(x)$在$X$上的一个上界

连续

$f(x)\in C[a,b]$则$f(x)$在$[a,b]$上有界

但开区间不一定满足有界

若有界则$\exists \lim{x\to a^+} f(x),\lim{x\to b^-} f(x)$

极限的性质

唯一性

若有极限，则必唯一

逆否：若左右极限不等，则极限不存在

局部有界性

函数与数列的区别是函数是连续的而数列是离散的

如$y=\frac1x$极限为$0$但无界

若$\displaystyle\lim_{x\to a}f(x)=A$，则$\exists \delta>0$，当$x\in \mathring{U}(a,\delta),|f(x)|\le M(M>0)$

反向

若$\displaystyle\lim_{x\to a}f(x)=A(A\ne 0)$，则$\exists \delta>0$，当$x\in \mathring{U}(a,\delta),|f(x)|>\left|\frac A2\right |(M>0)$

单侧有界性

可单侧使用

若右极限存在，则在右邻域中有界

保号性

若$\displaystyle\lim_{x\to a}f(x)=A>0$，则$\exists \delta>0$，当$x\in \mathring{U}(a,\delta),f(x)>0$

复合函数

$y=f[\varphi(x)]$==其中$\varphi (x)\ne a $==，若

$\lim_{x\to x_0}\varphi(x)=a,\lim_{x\to a}f(x)=A\Rightarrow\\ \lim_{x\to x_0}f[\varphi(x)]=A$

$f(x)$可能在$a$处无定义

连续与间断

定义，若$f(x)$在$x_0$的邻域(不去心)有定义，且

$\lim_{\Delta x\to0}\Delta y=\lim_{\Delta x\to0}f(x_0+\Delta x)-f(x_0)=0$

等价定义(三合一)，必须双向逼近

$\lim_{x\to x_0}f(x)=f(x_0)=\lim_{x\to x_0^+/x_0^-}f(x)$

特点:

在邻域有定义$\exists f(x_0)$
左右极限存在且相等
等于函数值

在区间上连续

开区间若每一点连续则在区间上连续

闭区间在端点处只要求单侧连续

基本初等函数在定义域上连续

初等函数在定义区间上连续($\text{not}$定义域)

反例$y=\sqrt{\sin x-1}$无邻域

运算

四则注意分母不为0

复合函数

$\lim_{x\to x_0}\varphi(x)=a,\lim_{x\to a}f(x)=f(a)=A\\ \Rightarrow\lim_{x\to x_0}f[\varphi(x)]=f[\lim_{x\to x_0}\varphi(x)]=f(a)$

内层不需要连续，连续则极限符号可交换

间断

首先有函数在去心领域有定义，其次不连续

介值定理

$f(x)$在$[a,b]$上连续，则对$\forall c\in[m,M]$，$\exists \xi\in[a,b],\text{s.t.}f(\xi)=c$

离散形式

数列满足$|a{n+1}-a{n}|\le1$则类比介值定理

零点定理

$f(x)$在$[a,b]$上连续，则若$f(a)f(b)<0$，$\exists \xi\in(a,b),\text{s.t.}f(\xi)=0$

实际上为零点定理的特殊形式

特殊函数

绝对值$|x|$，$0$处连续但不可导

$\lim_{x\to0}\frac{f(x+h)-f(x-h)}h=0$

曲线光滑不一定可导

$y=x^{\frac13},y’=\frac{1}{3x^{\frac23}},x\to0,y’=\infty$
导数存在不一定连续可导(导函数连续)
$f(x)=\begin{cases}x^2\sin \frac1x,x\ne0\\ 0,x=0\end{cases}$

符号函数

$x=|x|\text{sgn}x \\ |x|=x\text{sgn}x$ $f(x)=\begin{cases}1,x\ge0\\ -1,x<0\end{cases}$

$|f(x)|$连续

$[x]\le x<[x]+1$

定义域为$\mathbf R$，值域为$\mathbf Z$

$[x]+[y]\le[x+y]\le[x]+[y]+1$

Dirichlet function

$\textbf{1}_{\mathbb{Q}}(x)=\begin{cases}1,x\in \mathbb{Q}\\ 0,x\notin \mathbb{Q}\end{cases}$

处处无极限，处处不连续，处处不可导

任意有理数都为其周期，无最小正周期，偶函数

$f(x)=\begin{cases}\frac1x,x\ne0\\ 0,x=0\end{cases},f(f(x))=x$

大一/c语言/循环

Posted on 2022-07-31

for

for(initalize;end statement;forward){   
}

for(int i=1;i<=10;i++) cout<<i;
//simplest case
//最重要的三要素(起点 更新 终点)

for (int i = 0, j = 100; i < j; i++)//可有多个变量

for 比while循环更加紧凑

STL容器的迭代

$\rm iterator$可直接迭代元素(类似指针)

vector<int> nums={1,3,5,7,9};
    for(vector<int>:: iterator iter=nums.begin();iter!=nums.end();iter++)
    cout<<*iter<<" ";//访问元素
1 3 5 7 9
    
//使用auto iter替换

while

while(A){
	//若A为真,则执行
    //注意A要在循环体中更新,否则为infinite loop
}
int i=1;
while(i<=10){
    cout<<i;
    i++;
}
//simplest case

while循环为top-checking loop，先检查表达式(A)

do-while

do
    stetament
while(condition);

如先输入变量再计算

break 跳出本层循环(不循环了)

continue 跳出本次循环(不执行后面的语句)

大一/c语言/选择

Posted on 2022-07-31

if

类型1

if(case A){
    //一条语句不用括号
}
else if(case B){
   //若一条符合则不会看后面的语句
}
else{
    
}

类型2

if(case 1)
if(case 2)//每条都会看

判断条件

$==\quad 等于\\ !=\quad 不等于\\ >/</>=/<= 比较大小\\ 关系运算\\ 逻辑与\;\;\&\& \rm= and\\ 逻辑或\;\;||=or\\ 逻辑非\;\; !=not$

表达式复杂勤用括号

三目运算符

 if(A) B
 else C
 
 可写成
 A?B:C//c++中唯一一个三目运算符
     //conditional expression
     
abs(int a)
=>(n < 0) ? -n : n
     
//多个 ‘?’
int i=(num<10)?5:
		(num>50)?10:
(num<50 && num>10)?20:30;
//循序渐进满足?否则执行后面的语句
int num=41
i=20

switch

switch(expression){//A 为一个常量表达式
    case A: ~~~(break);
    case B: ~~~(break);
    default://都不符合
}

int main(){
    char a;
    cin>>a;
    switch (a)
    {
    case 'a':
        printf("is a\n");
        break;
    default:
        cout<<"not a"<<endl;
        break;
    }
}//A 为一个常量表达式

If the case label matches the switch’s expression, then the statements that follow that label are executed up until the break statement is encountered.

若没有break，一直执行，直到break

Shiwei Pan

Open your eyes,look up to the skies

GitHub LinkedIn