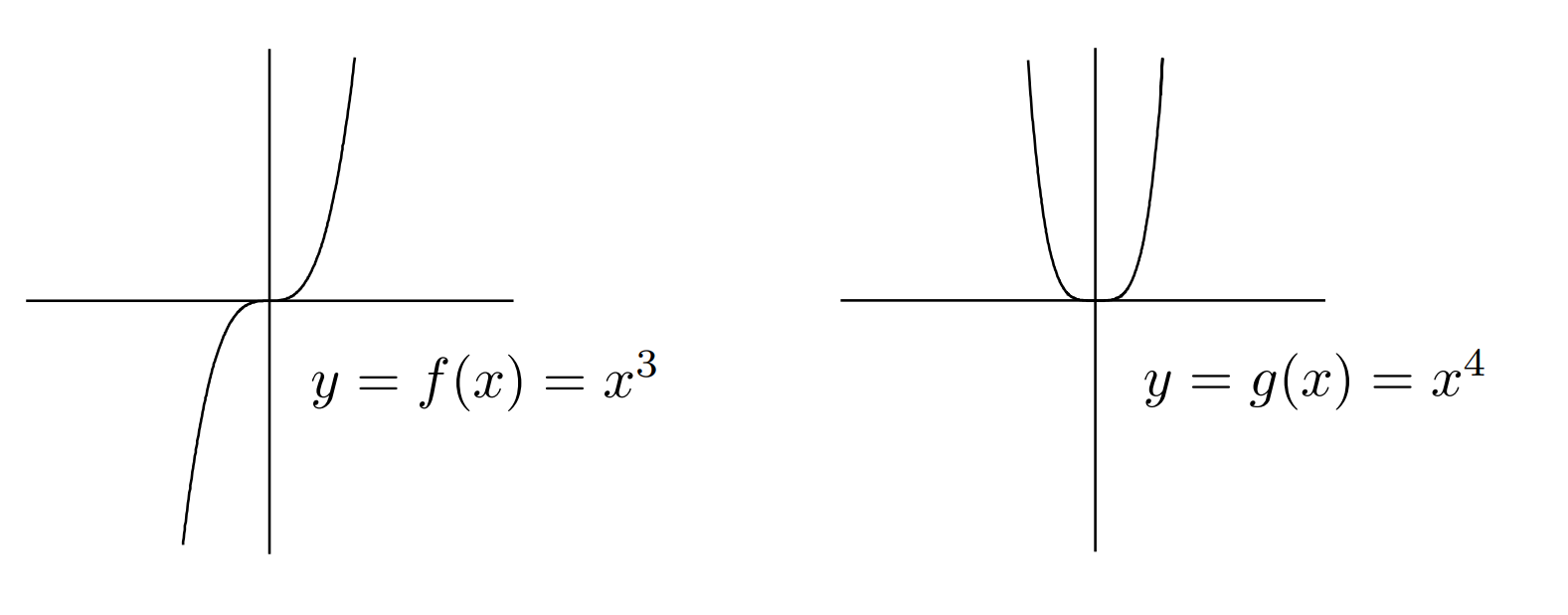大一/物理/力学

Posted on 2022-10-02

牛顿定律

第一定律

若没有外力来改变物体的运·动状态，任何物体都将保持静止或做匀速直线运动的状态

$\boldsymbol{v}=\vec C(\boldsymbol{F}=0\Rightarrow\boldsymbol{a}=0)$

其又称为惯性定律，指出力是改变物体运动状态的原因

第二定律

$\boldsymbol{F}=k\frac{\text{d}\boldsymbol{p}}{\text{d}t}$

在$\text{SI(International System of Unit)}$中，$k=1$

一般情况下

$\boldsymbol{F}=M\boldsymbol{a}(\frac{\text{d}M}{\text{d}t}=0)$

第三定律

当两个物体相互作用时，相互作用力

$\boldsymbol{F}_{12}=-\boldsymbol{F}_{21}$

非惯性系

对一个以加速度$\boldsymbol{a}$做加速运动的参考系，牛顿定律不成立

若该系中物体受到一个$-m\boldsymbol{a}$的惯性力，则成立

生活中的超失重现象可由此解释

动量守恒定律

若$\sum F_{\text{external}}=0 $或更充分的不受外力

也可$\sum F{\text{external}}\ll\sum F{\text{internal}}$

$\boldsymbol{p}_1+\boldsymbol{p}_2=\boldsymbol{p}'_1+\boldsymbol{p}'_2\\ m\boldsymbol{v}_1+M\boldsymbol{v}_2=m\boldsymbol{v}'_1+M\boldsymbol{v}_2'$

移项可得$\Delta\boldsymbol{p}_1+\Delta\boldsymbol{p}_2=0,\Delta m\boldsymbol{v}_1+M\Delta\boldsymbol{v}_2=0$

由牛顿第三定律也可推出

动量定理

冲量等于动量变化量

$\int_{t_1}^{t_2}\boldsymbol{F}\text{d}t=\boldsymbol{p}_2-\boldsymbol{p}_1$

由积分中值公式

$\overline{\boldsymbol{F}}=\frac{\displaystyle\int_{t_1}^{t_2}\boldsymbol{F}\text{d}t}{t_2-t_1}=\frac{\boldsymbol{p}_2-\boldsymbol{p}_1}{t_2-t_1}\\ \Rightarrow \boldsymbol{I}=\int_{t_1}^{t_2}\boldsymbol{F}\text{d}t=\overline{\boldsymbol{F}}(t_2-t_1)$

对于质点组，我们可以对每一个物体运用再求和

容易看出合外力的冲量等于总动量的变化量

并且$\sum F_{\text{internal}}=0$，故内力不能改变总动量

质心

$\boldsymbol{r}_c=\frac{ \sum m_i\boldsymbol{r}_i}{\sum m_i}$

一般我们为了计算，将其分解到三个轴的方向上

对于连续的物体，

$\boldsymbol{r}_c=\frac{ \displaystyle\int_V \boldsymbol{r}_i\text{d}m}{M}$

对两边求导得

$\boldsymbol{a}_c/\boldsymbol{v}_c=\frac{\sum m_i\boldsymbol{a}_c/\boldsymbol{v}_i}{\sum m_i}$

前提是质量不变

$\boldsymbol{p}=\sum m_iv_i\\ \sum\boldsymbol{F}=\frac{\text{d}\boldsymbol{p}}{\text{d}t}=M\boldsymbol{a}_c$

利用等效替代的思想可以很容易理解质心

质心与动量守恒

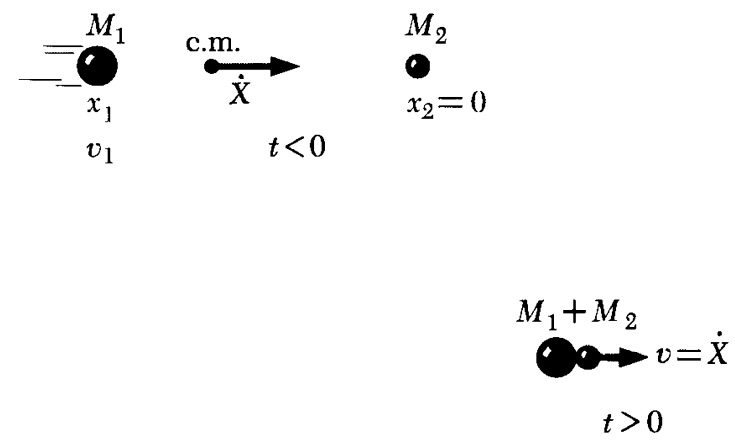
初始时，质心的运动速度

$v_c=\frac{M_1v_1+M_2\cdot0 }{M_1+M_2}=\frac{M_1v_1 }{M_1+M_2}$

由动量守恒得到相同的结果

从质心看，两个物体组成的系统运动状态保持不变

考虑碰撞前后动能的比值

$\frac{E_{k2}}{K_{k1}}=\frac{M_1 }{M_1+M_2}$

质心参考系

$v_c=\frac{M_1v_1 }{M_1+M_2}\\ u_1=v_1-v_c=\frac{M_2v_1 }{M_1+M_2}\\ u_2=0-v_c=-\frac{M_1v_1 }{M_1+M_2}$ $M_1u_1+M_2u_2=0$

在质心参考系中，两动量一直等大反向

$v_{AB}=v_{AS}-v_{BS}$

推广

$\begin{aligned} \boldsymbol{P}^{\prime} &=\sum_{i=1}^{N} m_{i} \boldsymbol{v}_{i}^{\prime} \\ &=\sum_{i=1}^{N} m_{i}\left(\boldsymbol{v}_{i}-\boldsymbol{v}_{C}\right) \\ &=\sum_{i=1}^{N} m_{i} \boldsymbol{v}_{i}-\sum_{i=1}^{N} m_{i} \boldsymbol{v}_{C} \\ &=\sum_{i=1}^{N} m_{i} \boldsymbol{v}_{i}-M \boldsymbol{v}_{C} \\ &=\boldsymbol{P}-\boldsymbol{P}_{C} \\ &=\mathbf{0} \end{aligned}$

质心系是一个零动量系

柯尼希定理

对于平动系$A$和质心系$S$，有$v{cA}=v{SA}=v_c$

对于动能，对速度

$v_i'=v_i-v_c\\ \Rightarrow E_{kS}=E_{kA}-\frac12Mv_c^2$

移项

$E_{kA}=E_{kS}+\frac12Mv_c^2$

质点系在参考系$A$中的总动能等于质点系在质心系中的动能与质心在参考系$A $中的动能之和

对前面一动一静作推广

在不同参考系下，$\boldsymbol{u}{12}=\boldsymbol{v}{1}-\boldsymbol{v}_{2}$

故在质心参考系下

$E_{kS}=\frac12\frac{M_1M_2}{M_1+M_2}(\boldsymbol{u}_{12})^2$

记$\mu=\frac{M1M_2}{M_1+M_2}$为折合质量，所以$E{kS}$又称为相对动能

能量守恒定律

动能定理

对某一个质点来说

$\sum F=m\frac{\text{d}v}{\text{d}t}=m\frac{\text{d}v}{\text{d}x}v$

两端积分得到

$\int _{x_1}^{x_2}\sum F\text{d}x=\frac12mv_2^2-\frac12mv_1^2$

由此，我们定义$\frac12mv^2$为动能$E_k(\text{kinetic})$

而$\displaystyle \int _{x_1}^{x_2}\sum F\text{d}x$称为合外力的功$(\text{work})$

若力和位移有夹角，则乘上$\cos \theta$

注意方向，如位移从大到小，则指明$\text{d}x$为负值

对于能量，我们考察重力所做的功

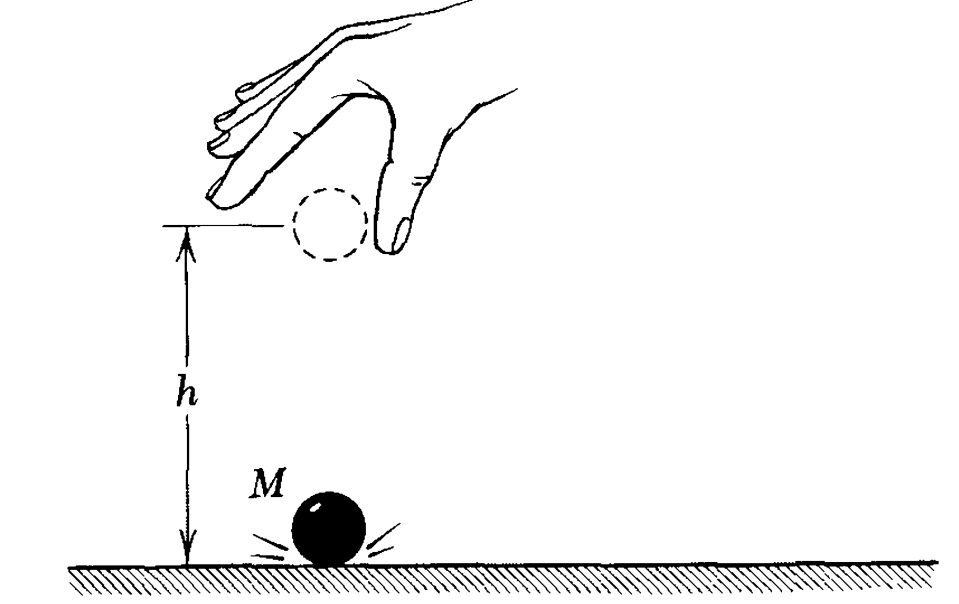
重力做了$Mgh$的功从而存在着重力势能，由此我们定义

物体在地球表面上方$h$处的重力势能为$Mgh$

势能即为物体能获得动能的能力

对与某一个过程来说，$W_G=-\Delta E_p=E_1-E_2$

若$E_2=0$则场力做的功为势能，反之

从势能零点用外力匀速移动物体所做的功为势能

注意，势能零点可以随意选取，原则上方便为主

因此不指定零点的势能是无意义的

写成微分形式$W_F=F\text{d}x=-\text{d}U$

故分解后有

$\boldsymbol{F}_{保}=-\left(\frac{\partial E_p}{\partial x }\boldsymbol{i} + \frac{\partial E_p}{\partial y }\boldsymbol{j} +\frac{\partial E_p}{\partial z }\boldsymbol{k} \right)\\ \boldsymbol{F}_{保}=-\nabla E_p$

保守力的方向沿势能降低最快的方向

功能原理

首先引入保守力的概念

若一个力为保守力，则它满足以下条件

$\oint F\text{d}x=0$

即保守力做功与路径无关

我们引入机械能的概念

$E_k+E_p=E$

由动能定理和势能和功的关系移项可知

若一个系统只有保守力做功，则机械能守恒

对质点组求和，易得

$W_外+W_{内非保守}=\Delta E$

角动量守恒

角动量指位矢和动量的叉乘

$\boldsymbol{L}=\boldsymbol{r}\times\boldsymbol{p}= m\boldsymbol{r}\times\boldsymbol{v}$

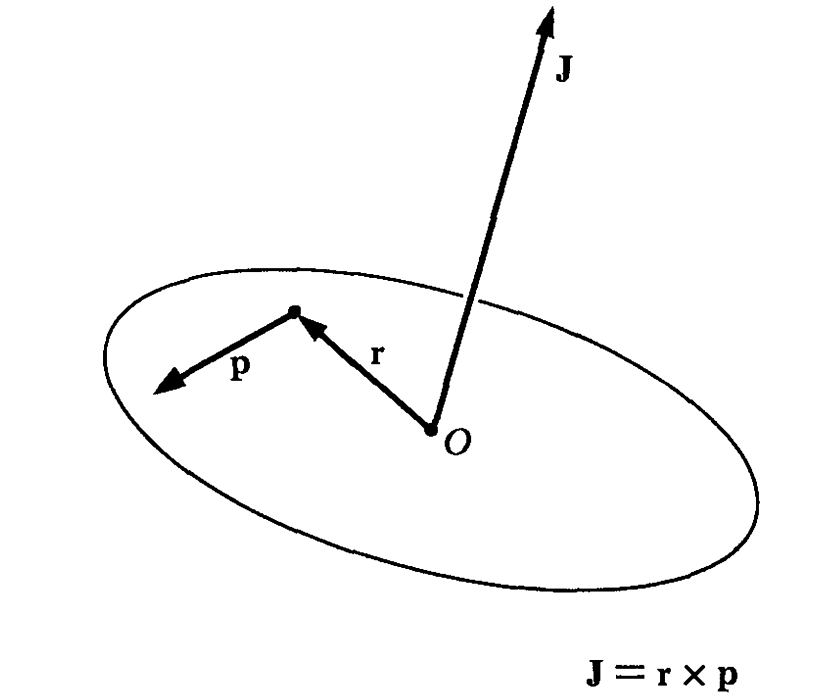
力矩

$\boldsymbol{M}=\boldsymbol{r}\times\boldsymbol{F}$

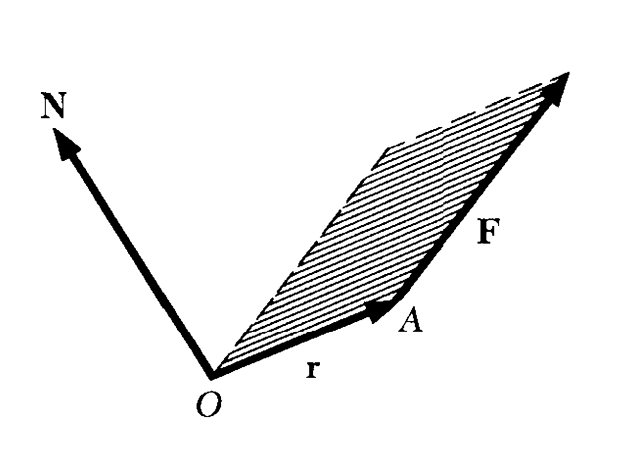
对$\boldsymbol{L}$

$\boldsymbol{M}=\frac{\text{d}\boldsymbol{L}}{\text{d}t}$

对$\boldsymbol{M}=0$，有角动量为一常量，即角动量守恒

对于有心力，$\sin \theta=0$，故也有角动量守恒

同时对系统来说内力所产生的力矩之和为$0$

力矩投影

我们一般研究力矩在某一轴上的投影，故还要乘上$\cos \gamma$

因为与轴平行的力产生的力矩与轴垂直

故只有在与轴垂直的平面内力的投影才有效

或称为垂直于轴的力$F_\perp $

有时外力矩的矢量不为$0$

而系统所受外力在某一轴上代数和为$0$

则系统对某轴角动量守恒

对于轴$\vec n$，取轴上任意一点$A$

$M_n(F)=\begin{vmatrix} e_x& e_y & e_z\\ r_x &r_y &r_z \\ F_x & F_y &F_z \end{vmatrix}$

大一/物理/运动

Posted on 2022-10-02

质点运动学

运动

质点为一个简化的忽略形状的物体，我们在选定的参考系(被选定的参考物体)下研究这个质点的运动情况

位矢

首先选取坐标原点，由此定义位矢$\vec r$

$\vec r=x \vec i+y\vec j+z\vec k$

位矢的方向由下式确定

$\cos \alpha=\frac x r,\cos \beta =\frac yr,\cos \gamma=\frac z r$

从而可以写出质点的运动方程

$\vec{r}=\vec{r}(t)=x(t) \vec i+y(t)\vec j+z(t) \vec k$

对于某一段过程，我们可以很自然地表示位移

$\Delta\vec r=\vec r(t_2)-\vec r(t_1)$

位移为矢量，$|\Delta\vec r|$表示两点的直线距离

速度

为了描述质点运动的快慢，我们引入速度的概念

$\overline{\vec v}=\frac{\vec r(t_2)-\vec r(t_1)}{t_2-t_1}$

这就是在某一段时间内的平均速度，方向为位移方向

当两个点$P_1,P_2$不断接近，割线变为切线

故速度也沿着切线方向

$\vec v=\lim_{\Delta t\to 0}\frac{\Delta \vec r}{\Delta t}=\frac{\text{d}\vec r}{\text{d}t}$

这也就是瞬间速度，$|\vec v|$被称为速率

同理可以正交分解，但还可以这样分解

在极坐标系下，有$r,\theta$两个参数

$\boldsymbol{v}=\frac{\text{d}r}{\text{d}t}\hat{\boldsymbol{r}}+r\frac{\text{d}\theta}{\text{d}t}\hat{\boldsymbol{\theta}}\\$

其中$\hat{\mathbf{r}}$是径向单位矢量，$\hat{\boldsymbol{\theta}}$是与径向垂直的单位矢量

加速度

同理，加速度即为速度对时间的导数，位移的二阶导数

$\vec a=\frac{\text{d}\vec v}{\text{d}r}= \frac{\text{d}^2\vec r}{\text{d}t^2}$

极坐标系下，有

$\boldsymbol{a}=\left[\frac{\text{d}^{2} r}{\text{d} t^{2}}-r\left(\frac{\text{d} \theta}{\text{d} t}\right)^{2}\right] \hat{\boldsymbol{r}}+\frac{1}{r}\left[\frac{\text{d}}{\text{d} t}\left(r^{2} \frac{\text{d} \theta}{\text{d} t}\right)\right] \hat{\boldsymbol{\theta}}$

自然坐标

因为速度延切线方向，故

$\boldsymbol{v}=\frac{\text{d}s}{\text{d}t}\boldsymbol{e}_t$

因为两个因子都是关于时间的函数

$\Rightarrow\vec a=\frac{\text{d}^2s}{\text{d}t^2}\boldsymbol{e}_t+v\frac{\text{d}\theta}{\text{d}t}\boldsymbol{e}_n$

故可以分解为切向加速度和法向加速度

关系

质点的运动方程是描述质点运动的核心

其中$\vec r,\vec v$被称为运动状态量，加速度$\vec a$被称为状态变化量

圆周运动

法向加速度

$\boldsymbol{a}_n=\frac{v^2}r=\omega^2r=\omega v$ $\boldsymbol{a}=\frac{\text{d}}{\text{d}t}(\boldsymbol{\omega \times \boldsymbol{r}})=\boldsymbol{\alpha \times \boldsymbol{r}}+\boldsymbol{\omega \times \boldsymbol{v}}$

运动方程

利用圆的参数方程可得

$\vec r(t)=R\cos(\omega t )\vec i+R\sin(\omega t)\vec i$

重要关系

$T=\frac1f\\ \omega=2\pi f$

相对运动

$\boldsymbol{v}_{ac}=\boldsymbol{v}_{ab}+\boldsymbol{v}_{bc}\\ \boldsymbol{a}_{ac}=\boldsymbol{a}_{ab}+\boldsymbol{a}_{bc}\\$

推论，当某一加速度为$0$时，保持不变

大一/高数/微分

Posted on 2022-09-29

微分的概念

函数值的变化量

$\Delta y=f(x_0+\Delta x)-f(x_0)$

对于复杂函数，$\Delta y$比较复杂

故我们将变化量线性化，定义为微分

若函数在某邻域有定义

$\Delta y=A\Delta x+o(\Delta x),\Delta x\to0$

则称$f(x)$在该领域可微，$\Delta y$的线性主部$A\Delta x$

为函数的微分，记为$\text{d} y|_{x=x_0}(\Delta x=\text{d} x)$

与导数的关系

可导$\Leftrightarrow$可微$\Rightarrow A=f’(x_0)$

微分形式不变性

$\text{d} y=f'(u)\text{d} u$

不论$u$是自变量还是函数都成立

微分中值定理

费马引理

若函数在某邻域$U(x_0)$有定义，且在$x_0$处可导，则若对于任意$x\in U(x_0)$，有 $f(x)\le f(x_0)$

$\Rightarrow f'(x_0)=0$

利用极限的保号性和夹逼

罗尔定理

若函数在闭区间$[a,b]$上连续，在开区间$(a,b)$上可导

若有$f(a)=f(b)$则

$\exists \xi\in(a,b)\quad\text{s.t.}f'(\xi)=0$

拉格朗日中值定理

若函数在闭区间$[a,b]$上连续，在开区间$(a,b)$上可导

则有

$\exists \xi\in(a,b)\quad\text{s.t.}f'(\xi)=\frac {f(b)-f(a)}{b-a}$

有限增量定理

若函数在闭区间$[x,x+\Delta x]$上连续，在开区间$(x,x+\Delta x)$上可导，则

$\exists \xi\in(a,b)\\ \text{s.t.}f'(x+\theta \Delta x)\Delta x=f(x+\Delta x)-f(x)$

推论

若$f(x)$在区间$I$上的导数恒为$0$，则在该区间上为常函数

柯西中值定理

若函数$f(x),g(x)$在闭区间$[a,b]$上连续，在开区间$(a,b)$上可导，且$g’(x)\ne0$

则有

$\exists \xi\in(a,b)\\ \text{s.t.} \frac{f'(\xi)}{g'(\xi)}=\frac {f(b)-f(a)}{g(b)-g(a)}$

达布中值定理

$f(x)$在$[a,b]$上连续

则导函数具有介值性，即可以取到$f’(a)$和$f’(b)$之间的一切值

同时导函数不具有第一类间断点3

泰勒公式

若函数$f(x)$在$I=(a,b),x_0\in I$处有$n(n\ge1)$阶导数，则

$\begin{aligned} f(x)&= f\left(x_{0}\right)+\frac{f^{\prime}\left(x_{0}\right)}{1 !}\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\cdots \\ &+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+o\left(\left(x-x_{0}\right)^{n}\right)\\ &=\sum_{i=0}^n\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+o\left(\left(x-x_{0}\right)^{n}\right) \end{aligned}$

$ o\left(\left(x-x_{0}\right)^{n}\right) $为佩亚诺余项，在某邻域上使用

泰勒中值定理

若函数$f(x)$在$I=(a,b),x_0\in I$处有$n+4(n\ge1)$阶导数，则

$f(x)=\sum_{i=0}^n\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+R_n(x)\\ R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1}\\ \xi \in(x_0,x)$

$R_n(x)$称为拉格朗日余项，在区间上使用

麦克劳林公式

若$x_0=0,\xi =\theta x$

$\begin{aligned} f(x)&=f(0)+f^{\prime}(0) x+\frac{f^{\prime \prime}(0)}{2 !} x^{2}+ \\ \quad &\cdots+\frac{f^{(n)}(0)}{n !} x^{n}+\frac{f^{(n+1)}(\theta x)}{(n+1) !} x^{n+1} \quad(0<\theta<1) . \end{aligned}$

$|f^{(n+1)}(\xi)|\le M$则有

$|R_n(x)|\le\frac{M}{(n+1)!}|x|^{n+1}$

例

$e^x=1+x+\frac1{2!}x^2+\cdots+\frac{e^{\theta x}}{(n+1)!}|x|^{n+1}$

常用

$\sin x = x - \frac{1}{3!} x^3 + \frac{1}{5!} x^5 - \frac{1}{7!} x^7 \ldots \qquad (x \in \mathbb R)\\ \cos x = 1 - \frac{1}{2!} x^2 + \frac{1}{4!} x^4 -\frac{1}{6!} x^6 \ldots \qquad (x \in \mathbb R)\\ \mathrm{e} ^x =1 + x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 \ldots \qquad (x \in \mathbb R)\\ \ln\left(1+x\right) = x - \frac12 x^2 + \frac13 x^3 - \frac14 x^4 \ldots \qquad (-1 < x < 1)\\ \frac{1}{1 \pm x} = 1 \mp x + x^2 \mp x^3 + x^4 \ldots \qquad (-1 < x < 1)\\ \sqrt{1\pm x} = 1 \pm \frac12 x - \frac18 x^2 \pm \frac{1}{16} x^3 - \frac{5}{128}x^4 \ldots \qquad (-1 < x < 1)\\ \tan x=x+\frac{x^3}3+\frac{2}{15}x^5\ldots\\ (1+x)^\alpha=1+\alpha x+\frac{\alpha(\alpha-1)}2 x^2+\cdots+\frac{\alpha(\alpha-1)\cdots(\alpha-n+1)}{n!}x^n\ldots$

拓展

$\frac1{1+x^2}=\sum_{i=0}^n(-1)^ix^{2i}+o(x^{2n+1})\\ \begin{aligned} \arctan x&=\sum_{i=0}^{2n}\frac{f ^{(i)}(0)} {i!}x^{i}\\&=\sum_{i=0}^n\frac{1}{(2i+1)!}\left.\left(\frac1{x^2+1}\right)^{(2i)}\right|_{x=0}x^{2i+1}\\ \\&=\int \frac1{1+x^2}\text{d}x\\ &=\sum_{i=0}^n\frac{(-1)^i}{2i+1} x^{2i+1}+ o(x^{2n+1})\end{aligned}$

泰勒展开没有普遍规律，但关键看余项的阶数，能够消掉余项就行

分式先看哪个好确定阶数，再上下同阶

洛必达法则

$\frac00$型

$\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} g(x)=0$
$g^{\prime}(x) \neq 0, \forall x \in \mathring{U}(a, \delta),f(x),g(x)可导$
$\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}=l(l \text { 为有限数或 } \pm \infty)$

$\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}=l$

洛必达法则为后验的，上下求导极限不存在而不能说明原极限不存在

$\frac\infty\infty$型

$\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} g(x)=\infty$
$g^{\prime}(x) \neq 0,\forall x \in \mathring{U}(a, \delta),f(x),g(x)可导$
$\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}=l(l \text { 为有限数或 } \pm \infty)$ $\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}=l$

其他类型同样可以通过化简变形可转化为上面两类

大一/高数/极限

Posted on 2022-09-02

$\varepsilon -N$定义

描述性定义：要多接近，有多接近

用$|a-b|$来描述距离

设${a_n}$为一个数列，$A$为某一常数，若对任意$\varepsilon>$0，都存在$N,N\in\mathrm{N}^+$使得当$n>N$时

$|a_n-A|<\varepsilon$

称$A$为${a_n}$趋于正无穷的极限，或${a_n}$称收敛于$A$

$\lim_{n\to\infty}a_n=A$

性质

唯一性

若数列${a_n}$收敛，则它的极限唯一

子数列的性质

对任意一个子数列${a_{n{_k}}}$

$\lim_{n_k\to\infty}a_{n_k}=\lim_{n\to\infty}a_n$

逆否命题

若存在两个子数列不收敛与同一常数，则原数列必发散

收敛于不同常数$(-1)^n$
至少有一个发散

有界性

对任意$n\in \mathrm{N}^+$，$\exists M>0$

$|a_n|\le M$

有界$\Leftrightarrow$同时有上界和下界

关系

若数列收敛则必有界，反之未必成立

保号性

若$\lim_{n\to\infty}a_n>0$，则$\exists N>0,n>N$时，有

$a_n>/<0$

加强形式

从某项起有$a_n>0$，则

$\lim_{n\to\infty}a_n\ge0$

审敛准则

夹逼定理

the sandwich principle(also known as the “squeeze principle”).

若$a_n\le b_n\le c_n$

$\lim_{n\to\infty}a_n=\lim_{n\to\infty}c_n=A\\ \Rightarrow\lim_{n\to\infty}b_n=A$

单调有界准则

单调有界数列必有极限

如${a_n}\uparrow$，则$a_1$为下界，若有上界则收敛，反之发散

运算法则

四则注意分母不为$0$

一定要两个极限都存在才可计算

$\lim_{x\to\infty}x-\lim_{x\to\infty}x\ne\lim_{x\to\infty}(x-x)$

还有子极限必须要存在，如

$\exists\lim _{h \rightarrow 0} \frac{f\left(x_{0}+2 h\right)-f\left(x_{0}-3 h\right)}{h}$

子极限不一定存在故不一定可导

反推可能有错误

重要极限

$\because x\ge0,\sin x\le x\le \tan x\\ \therefore1\le \frac x{\sin x}\le \frac1{\cos x}\\ \because\lim_{x\to0}\frac1{\cos x}=1\\ \therefore\lim_{x\to0}\frac x{\sin x}=1$ $\lim_{x\to \infty}\left(1+\frac1x\right)^x=e$

无穷小

在某一个极限过程中$(x\to x_0/\infty)$，$ \lim\alpha (x)=0$

则称$\alpha (x)$为$(x\to x_0/\infty)$的无穷小

无穷小可以与极限相互转化

$\lim f(x)=A\Leftrightarrow \lim(f(x)-A)=\alpha$

定理

有限个无穷小之和是无穷小，有界函数与无穷小之积是无穷小

等价无穷小

若$\alpha,\beta$为同一变化过程的两个无穷小，$\lim\frac\beta \alpha$为这个过程的极限

$\lim\frac\beta \alpha=0$，则$\beta$为$\alpha$的高阶无穷小，记为$\beta=o(\alpha)$
$\lim\frac\beta \alpha=c$为同阶无穷小$c\ne 0$
$\lim\frac\beta \alpha=1$则为等价无穷小，记为$\beta\sim\alpha$
$\lim\frac\beta {\alpha^k}=c(c\ne 0)$则称$\beta$为关于$\alpha$的$k$阶无穷小

特别的，对于等价无穷小$\beta\sim\alpha$，有

$\beta=\alpha+o(\alpha)$

代换原则，乘积可代换，加减若上下同阶可代换

$\sin x \sim x \sim \tan x \sim\arcsin x \sim \arctan x\\ 1-\cos ^mx \sim \frac{mx^{2}}{2}, \ln (1+x) \sim x\\ e^x-1\sim x,\frac{a^x-1}x\sim\ln a\\ \tan x-x\sim\frac13x^3\sim x-\arctan x\\ x-\sin x\sim\frac16x^3\sim\arcsin x-x\\ x-\ln(x+1)\sim\frac12x^2\\(1+x)^\alpha-1\sim +\alpha x$

渐近线

$\lim_{x\to \infty}f(x)=A\Rightarrow y=A为水平渐近线\\ \lim_{x\to x_0^+/x_0^-}f(x)=\infty\Rightarrow x=x_0为铅直渐近线\\ k=\lim_{x\to \infty}\frac{f(x)}x,b=\lim_{x\to \infty}[f(x)-kx]$

大一/杂/adobe

Posted on 2022-08-29

PS

快捷键

限制比例shift

Ctrl+Alt+R选择并遮住

通过拷贝建立一个图层【Ctrl】+【J】(如选择了区域)

ctrl+d取消选择

删除delete

Alt + 鼠标右击调整画笔大小，alt取色

按住V后可用鼠标拖动图片

Alt+Del键即可把该颜色填充入当前图层（另外Ctrl+Del键是填充背景色）

功能

蒙版

下方有蒙版选项黑色隐藏白色显示

蒙版和图像关联，所以对蒙版操作会影响图像

混合模式两个图层的混合

图像调整调色ctrl+u

减去前面的形状用于反选

变换用于调整形状

AE

快捷键

剃刀工具ctrl+shift+D

下一帧PgDn

缓入缓出型关键帧F9

帧入点关键帧可以按键盘shift+F9实现,出点是ctrl+shift+F9实现

CapsLK刷新控制

CTRL+K打开合成设置

按住Ctrl，鼠标点住左键往左拖动笔刷变小；往右拖动笔刷变大。

pr

上下切换轨道

源浏览器中有仅添加音频和视频

用音轨选择器来调整音量

在“Effect Controls”（效果控制）面板中，在“Opacity”（不透明度）下的“Blend Mode”（混合模式）菜单中选择一种混合模式

shift 多选

交叉溶解yyds

在关键帧右键贝塞尔曲线

大一/python/basis/class

Posted on 2022-08-22

构造函数

1
2
3

class A:
	def __init__(self,param):
        self.a=param

在实例化对象时自动运行此方法，前后两个下划线为了防止冲突

$\rm self$必须为第一个参数,运行时会自动传入，代表实例本身

属性和方法

.attribute_name访问对象的某个属性

属性可为全新的类

.method_name(params)访问某个方法

继承

父类$\rightarrow$子类，继承了属性和方法

class child_class(parent_class):
    def __init__(self,attributes):
        super().__init__(attributes)
        self.other_attri=1

$\rm super$代表superclass即父类，子类称为subclass

覆盖原方法

直接重写，python会忽略父类中的方法

魔法方法

sub,mul等方法用于重载运算符

1	def __repr__()#用于重写print

大一/web/css

Posted on 2022-08-20

Grid

2D排版方式定义

$\text{display: grid}$

分割

    grid-template-rows: 100px 100px 50px;#垂直,分割行数值为间隔
grid-template-columns#水平

居中元素
align-items: center;
place-items: center;
间隔
row-gap: 10px

按比例分配 1fr 3fr 1:3分割
4*1fr 等价于 repeat(4,1fr)

子对象

#起始为1
grid-area:1/1/4/3

行首/列首/行尾/列尾
grid-row: 1/4;
grid-column: 1/3;

从哪开始延伸
1/ span 3

动画

使用animate.css

<link href="https://cdn.bootcdn.net/ajax/libs/animate.css/4.1.1/animate.min.css" rel="stylesheet">

使用class来应用动画
<h1 class="animate__animated animate__bounce">
需要animate__前缀

然后可以在对象中指定参数

#ele{
    animation-duration: 2s;
    animation-delay: 2s;
    animation-timing-function:
}

关键帧

div{
animation-name:mymove;
animation-duration:3s;时间
animation-timing-function:ease-in-out;
}

@keyframes mymove{
    0%   {width:50px;height:50px;}	
    50%   {width:100px;height:100px;}	
    100%   {width:50px;height:50px;}
}

animation-iteration-count：检索或设置对象动画的循环次数

变量

CSS变量可以访问 DOM

:root{ 
  --bg-color: #cccccc;
}
{ 
  color: var(--primary-color, blue);
}
用var来插入变量
自定义属性有前缀--
从而可以快速改变css属性 	
也可以使用 fallback values，以便在自定义属性没有被定义时使用默认值

JS

.css("color","blue") (JQuery)
.style
如果样式是通过外部样式表或者通过浏览器的默认样式设置的，则无法通过.style对象访问这些样式
.style.setProperty('--animate-duration', '2s');(DOM对象)
//获取具体内容
var element = document.querySelector('.my-element');
var style = window.getComputedStyle(element).'::before';
var content = style.getPropertyValue('content');

getComputedStyle 方法只能用于获取元素的最终渲染样式，不能用于获取元素的原始样式

效果

1 2	box-shadow: offset-x \| offset-y \| blur-radius \| spread-radius \| color

伪元素

::before/::after
在前或在后面
.sub_title::after{
    content: "";
    position: absolute;
    border-bottom: 5px solid black;
    height: 30px;
    transform: translate(-50%,50%);}

大一/python/DL/api

Posted on 2022-08-17

导入

1
2
3

from torch.utils import data
import torch
from torch import nn#neural network

数据

trans = torchvision.transforms.ToTensor()#变换为张量
mnist_train = torchvision.datasets.MNIST(
    root="./data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.MNIST(
    root="./data", train=False, transform=trans, download=True)

train_iter=data.DataLoader(mnist_train,256,True)
test_iter=data.DataLoader(mnist_test,256,True)
#变成一个迭代器

注意labels的形状为$m\times 1$而非$m$

返回一个迭代器，用$\rm next(iter(data))$来访问

网络结构

#先定义参数
def init_weight(m):
    if type(m)==nn.linear:
        nn.init.normal_(m.weight,std=0.01,mean=0)
#不能用randn,太大了
net.apply(init_weight)
net=nn.Sequential(nn.Linear(2,1))

优化

loss=nn.MSELoss()#损失函数
trainer=torch.optim.SGD(net.parameters(),lr=0.03)
#实例化优化器

for epoch in range(epochs):
    for X, y in data_iter:#迭代器每次返回X和y
        l = loss(net(X) ,y)
        trainer.zero_grad()#清零梯度
        l.backward()
        trainer.step()#自动前进
    l = loss(net(feature), lables)#每轮再计算loss
    print(f'epoch {epoch + 1}, loss {l:f}')

大一/高数/导数

Posted on 2022-08-15

导数

切线

本质上是割线两个点趋向一起

$y-y_0=f'(x_0)(x-x_0)$

定义

若函数$f(x)$在点$x_0$处的某邻域有邻域可导，则

$\left.\frac{\text{d}f(x)}{\text{d}x}\right|_{x=x_0}=\left.\frac{\text{d}y}{\text{d}x}\right|_{x=x_0}=f'(x_0) \\f'(x_0)=\lim_{\Delta x\to0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

同理$\Delta x\to0^-/0^+$可用于定义左右导数

可导

左右导数存在且相等(双侧)

可导一定连续，而连续不一定可导

$y=|x|$有尖点
曲线光滑不一定可导

$y=x^{\frac13},y’=\frac{1}{3x^{\frac23}},x\to0,y’=\infty$
导数存在不一定连续可导(导函数连续)
$f(x)=\begin{cases}x^2\sin \frac1x,x\ne0\\ 0,x=0\end{cases}$

$n$阶可导$\Rightarrow$ $n-1$阶连续可导

上下无穷小必须同阶才可凑出导数形式

导数极限定理

如果$ f(x) $在$ x_0 $的邻域内连续，在$ x_0 $的去心领域内可导，且导函数在$ x_0 $出的极限存在，则$ f(x) $在$ x_0 $处的导数也存在并且等于导函数的极限

导函数左极限存在蕴含左导数存在，导函数右极限存在蕴含右导数存在

亚导数

将导数拓展到不可微的函数

$y=|x|\\ \frac{\partial|x|}{\partial x}=\left\{\begin{array}{ll} 1 & \text { if } x>0 \\ -1 & \text { if } x<0 \\ a & \text { if } x=0, \end{array} \quad a \in[-1,1]\right.$ $\frac{\partial}{\partial x}\max(x,0)=\left\{\begin{array}{ll} 1 & \text { if } x>0 \\ 0 & \text { if } x<0 \\ a & \text { if } x=0, \end{array} \quad a \in[0,1]\right.$

隐函数求导

等式左右两边看成两个函数

$f(x)=g(x)\Rightarrow f'(x)=g'(x)$

参数方程求导

$\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}t}\bigg/\frac{\text{d}x}{\text{d}t}$

结果为关于$t$的函数

反函数

$\frac{\text{d}y}{\text{d}x}=1\bigg/\frac{\text{d}x}{\text{d}y}$

结果往往用$y$来表示，但是带入数值结果等价

(关于$y=x$对称故有此结果)

高阶导数

递推定义

$f^{(n)}(x)=\begin{cases}[f^{(n-1)}(x)]',n\ge 1\\ f(x),n=0\end{cases}$ $(\sin x)^{(n)}=\sin(x+\frac{n\pi}2)\\ (\cos x)^{(n)}=\cos(x+\frac{n\pi}2)$ $(x^n)^{(n)}=n!,(x^n)^{(n+1)}=0$ $\left(\frac1x\right)^{(n)}=(-1)^n\frac{n!}{x^{n+1}}\\ \Rightarrow\left(\frac1{ax+b}\right)^{(n)}=({\color{red}{-a}})^n\frac{n!}{(ax+b)^{n+1}}\\$

莱布尼兹公式

$(uv)^{(n)}=\sum_{i=1}^nC_n^iu^{(n-i)}v^{(i)}$

证明题使用数学归纳法来证明

导数公式

$(x^a)'=ax^{a-1}\\ (a^x)'=\ln a \cdot a^x \\(\log_ax)'=\frac{1}{\ln a\cdot x }\\ (\sin x)'=\cos x\\ (\cos x)'=-\sin x$ $[f(x)\pm g(x)]'=f'(x)\pm g'(x) \\ [f(x)\cdot g(x)]'=f'(x)g(x)+f(x)g'(x)\\ \left (\frac{f(x)}{g(x)}\right)'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\\ [f(g(x))]'=f'(g(x))\cdot g'(x)$ $\frac {\text{d}}{\text{d}x}(\tan x)=\sec^2x\\ \frac {\text{d}}{\text{d}x}(\cot x)=-\csc^2x\\ \frac {\text{d}}{\text{d}x}(\sec x)=\tan x \sec x\\ \frac {\text{d}}{\text{d}x}(\csc x)=-\cot x \csc x\\$ $\frac {\text{d}}{\text{d}x}(\arcsin x)=\frac1{\sqrt{1-x^2}}\\ \frac {\text{d}}{\text{d}x}(\arccos x)=-\frac1{\sqrt{1-x^2}}\\ \frac {\text{d}}{\text{d}x}(\arctan x)=\frac1{1+x^2}\\ \frac {\text{d}}{\text{d}x}(\text{arccot} x)=-\frac1{1+x^2}\\ \frac {\text{d}}{\text{d}x}(\text{arcsec} x)=\frac1{ { {\color{red}{|x|}}}\sqrt{x^2-1}}\\ \frac {\text{d}}{\text{d}x}(\text{arccsc} x)=-\frac1{ {\color{red}{|x|}}\sqrt{x^2-1}}\\ (\sinh x)'=\left(\frac{e^x-e^{-x}}2\right)' =\cosh x\\ (\cosh x)'=\left(\frac{e^x+e^{-x}}2\right)' =\sinh x\\$ $\frac{\text{d}}{\text{d} x} \cosh ^{-1}(x)=\frac{1}{\sqrt{x^{2}-1}}\\ \frac{\text{d}}{\text{d} x} \sinh ^{-1}(x)=\frac{1}{\sqrt{x^{2}+1}}$

应用

单调性

本质定义

$\forall x_1,x_2\in D,x_1<x_2,f(x_2)-f(x_1)>0\Rightarrow f(x)\uparrow$

充分条件

若可导函数$f(x)$在$[a,b]$上单调增加，则在区间$(a,b)$上导数$f’(x)>0$

反过来

在区间$(a,b)$上导数$f’(x)>0$，则$f(x)$在$[a,b]$上单调增加

推论只有有限多个导数为$0$的点(驻点)，则这个函数仍单调增加

讨论三类边界点(驻点，不可导点)

例$y=(2x-5)\sqrt[3]{x^2}$

$y'=\frac{10}3\frac{x-1}{\sqrt[3]{x}}$

$x$	$(-\infty ,0)$	$0$	$(0,1)$	$1$	$(1,\infty)$
$f’(x)$	$+$		$-$	$0$	$+$
$f(x)$	$\uparrow$	$0$	$\downarrow$	$-3$	$\uparrow$

一般步骤

求出驻点和不可导点(包括不连续)
用上述这些点将定义域划分为若干区间
判断$f’(x)$在每个区间上的符号
整合结果得到单调性

凹凸性

fig4-5-1

$\forall x_1,x_2\in D,f\left(\frac{x_1+x_2}2\right)>\frac{f(x_1)+f(x_2)}2$

则称函数$f(x)$的图像在区间上是凸的或称为凸函数

推广

$\forall x_i\in D,f\left(\sum_{i=1}^n\lambda_i x_i\right)>\sum_{i=1}^n\lambda_if(x_i)\quad \sum_{i=1}^n\lambda_i=1$

拐点

连续曲线上凸弧和凹弧的分界点

$f’’(x_0)=0$，则以上点都满足条件

$ (x_0,f(x_0))$可为有水平切线或为极值点

在该点不可导但仍可为拐点

同理$f’’(x_0)=0$还需看三阶导数

若函数在$x_0$有$2n+1 $阶导数

第一充分条件

==$f(x)$在$x_0$处连续==，且在，$\mathring{U}(x_0)$二阶可导

$x\in\mathring{U}^-(x_0) ,f''(x)>0\\ x\in\mathring{U}^+(x_0) ,f''(x)<0$

则$ (x_0,f(x_0))$为拐点

在两侧二阶函数异号

第二充分条件

类比$f’’’(x_0)\ne0$

第三充分条件

$f'(x_0)=f''(x_0)=\cdots=f^{(2n)}(x_0)=0\\ f^{(2n+1)}(x_0) <0$

极值

注意区分费马引理

若$\exists U(x_0)\subset D$，对于$\forall x\in \mathring{U}(x), f(x_0)>f(x_0)$

则称$f(x_0)$为函数的一个极大值

不一定要求连续，有定义就行，例如

0bd162d9f2d3572c80d42fa39a13632762d0c39f

极值定理

$\text{Extreme Value Theorem}$

$\frac{f(c+h)-f(c)}{h}\\ A:\lim_{h\to0^+}\cdot\lim_{h\to0^-}<0\\ B:\lim_{h\to0}=0$

推出若$x_0$为极值点则$f’(x_0)=0$为或不可导

判别法

第一充分条件

==$f(x)$在$x_0$处连续==，且在，$\mathring{U}(x_0)$可导

$x\in\mathring{U}^-(x_0) ,f'(x)>0\\ x\in\mathring{U}^+(x_0) ,f'(x)<0$

在两侧导函数异号

第二充分条件

若函数在$x_0$处有二阶导数

$f'(x_0)=0,f''(x_0)<0$

则为极大值点

第三充分条件

$f'(x_0)=f''(x_0)=\cdots=f^{(2n-1)}(x_0)=0\\ f^{(2n)}(x_0) <0$

类比为极小值点

最值

在区间$I$上，若对于任意$x\in I$，存在$x_0\in I$，都有$f(x)\le f(x_0)$

则称$f(x_0)$为函数在该区间上的最大值

若在闭区间$[a,b]$上连续，有限多个驻点和不可导点

则计算处各驻点$x_i$和不可导点$x’_j$

$\max_{x\in[a,b]}f(x)=\max\{f(x_1),\cdots,f(x_i),f(x_1'),\cdots,f(x_j'),f(a),f(b)\}$

大一/web/jQuery

Posted on 2022-08-12

JQuery

$\rm jQuery $是一个$\rm JavaScript $库。

导入

所有 jQuery 函数位于一个 document.ready 函数中，防止未加载完全就运行

$(document).ready(function(){
 
   // 开始写 jQuery 代码...
 
});

//简洁写法
$(function(){
 
   // 开始写 jQuery 代码...
 
});

选择器

三种类型

$("button").click(function(){
   $("p").hide();//据html元素类型
   $("#test").hide();//据id
   $(".test").hide();//据class
 });

事件

hover

$("p").hover(function(){
    $("p").css("background-color","yellow");//移动在上面
},// mouseenter
             function(){
    $("p").css("background-color","pink");//移开
    // mouseleave
});

which

//keydown - 键按下的过程
//keypress - 键被按下
//keyup - 键被松开

$("input").keydown(function(event){
    console.log(event.which);
});

Shiwei Pan

Open your eyes,look up to the skies

GitHub LinkedIn