公理

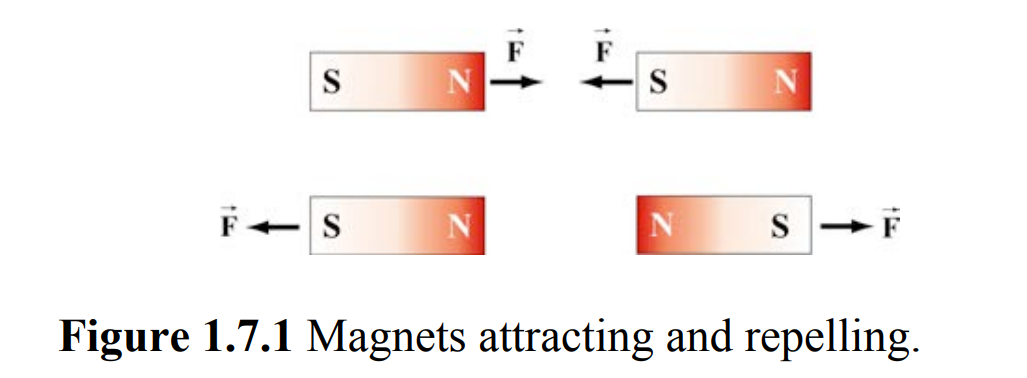
力的平行四边形法则

$$\vec{F_R}=\vec{F_1}+\vec{F_2}$$

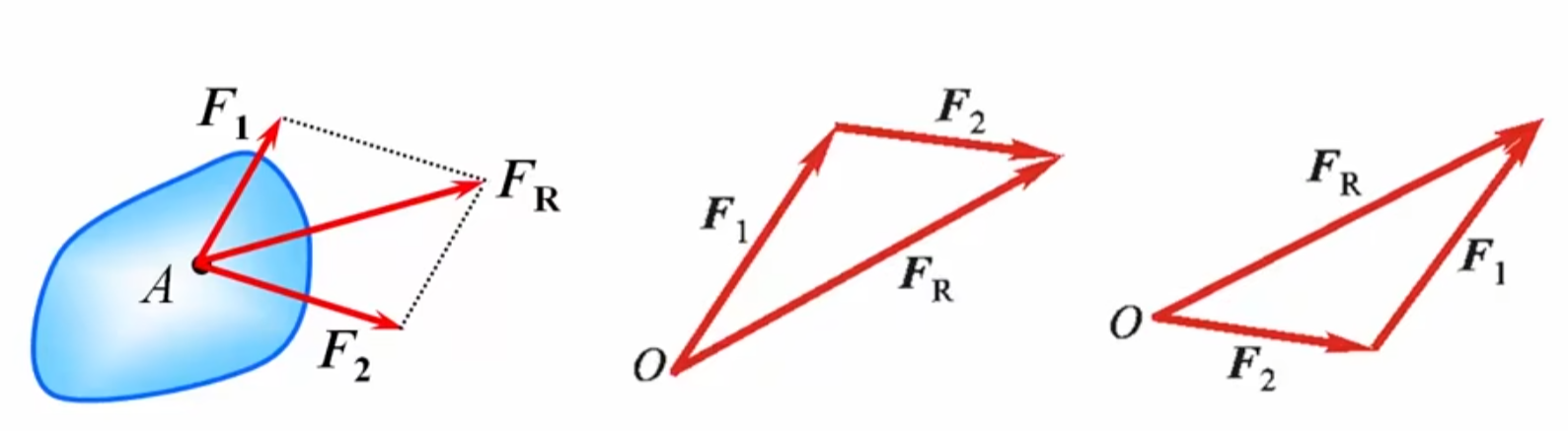
二力平衡

作用在刚体上的两个力，使刚体保持平衡的条件为两个力大小相等方向相反作用在同一条直线上

$$\vec{F_1}=-\vec{F_2}$$

加减平衡力系原理

在已知力系上加上或减去任意的平衡力系不改变作用效果

力的可传性

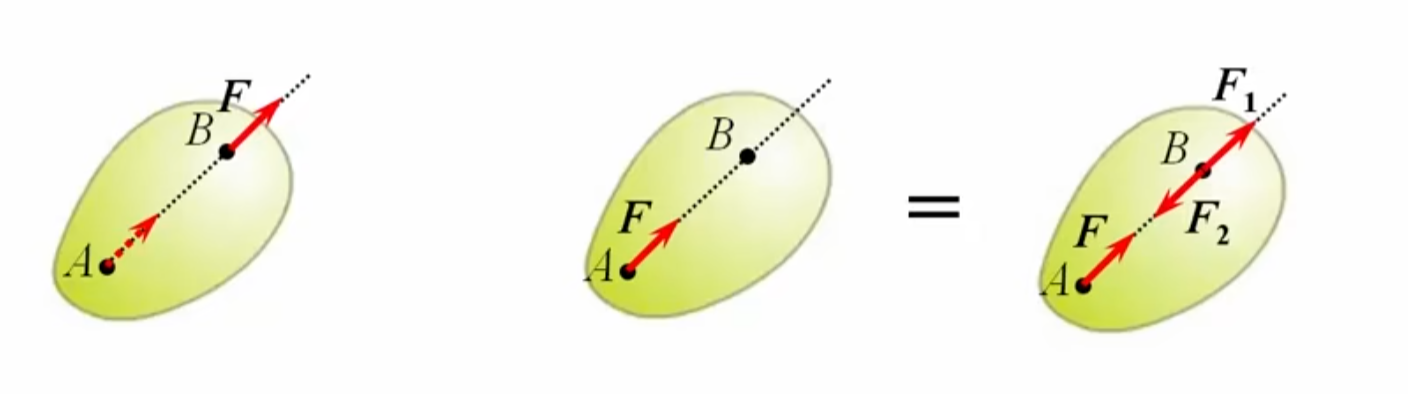
作用于某刚体上的力可以沿作用线移动到刚体内部任意一点，力为滑移矢

三力平衡汇交定理

由可传性可以推广到一般情况，若三力平衡则必共点且共面

牛三

作用力和反作用力等值反向共线作用在相互作用的两个物体上

刚化原理

变形体在力作用下平衡后如果把变形体变回刚体则状态不会改变

函数

多元函数

$$w=f(x_1,x_2,\dots,x_n)$$

二元函数

$$f(x,y)$$

定义域

$$w=\sqrt{y-x^2},y\ge x^2$$

去心邻域

$$\mathring{U}(P_0,\delta)=\{P|0<|PP_0|<\delta\}$$

若存在某邻域使得$U(P)\subset R$则为内点，反之为外点

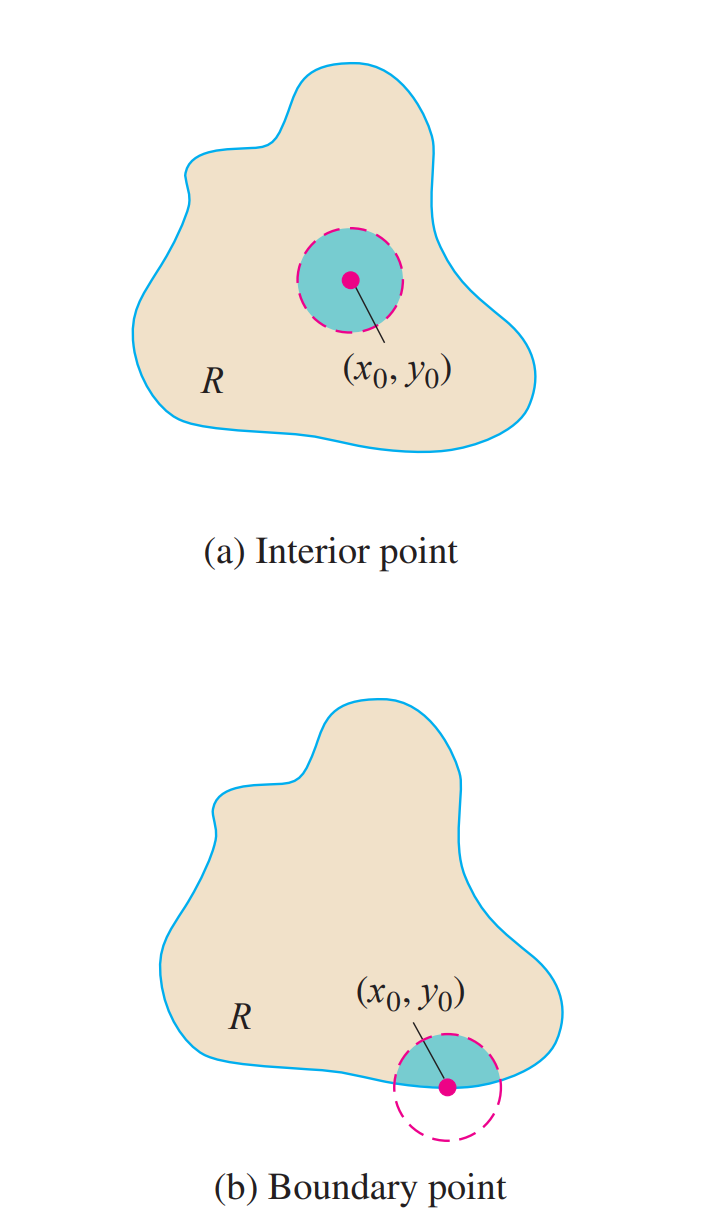
若有一部分属于，一部分不属于则为边界点

若所有的点都为内点则为开集，若边界$\partial R\subset R$则为闭集

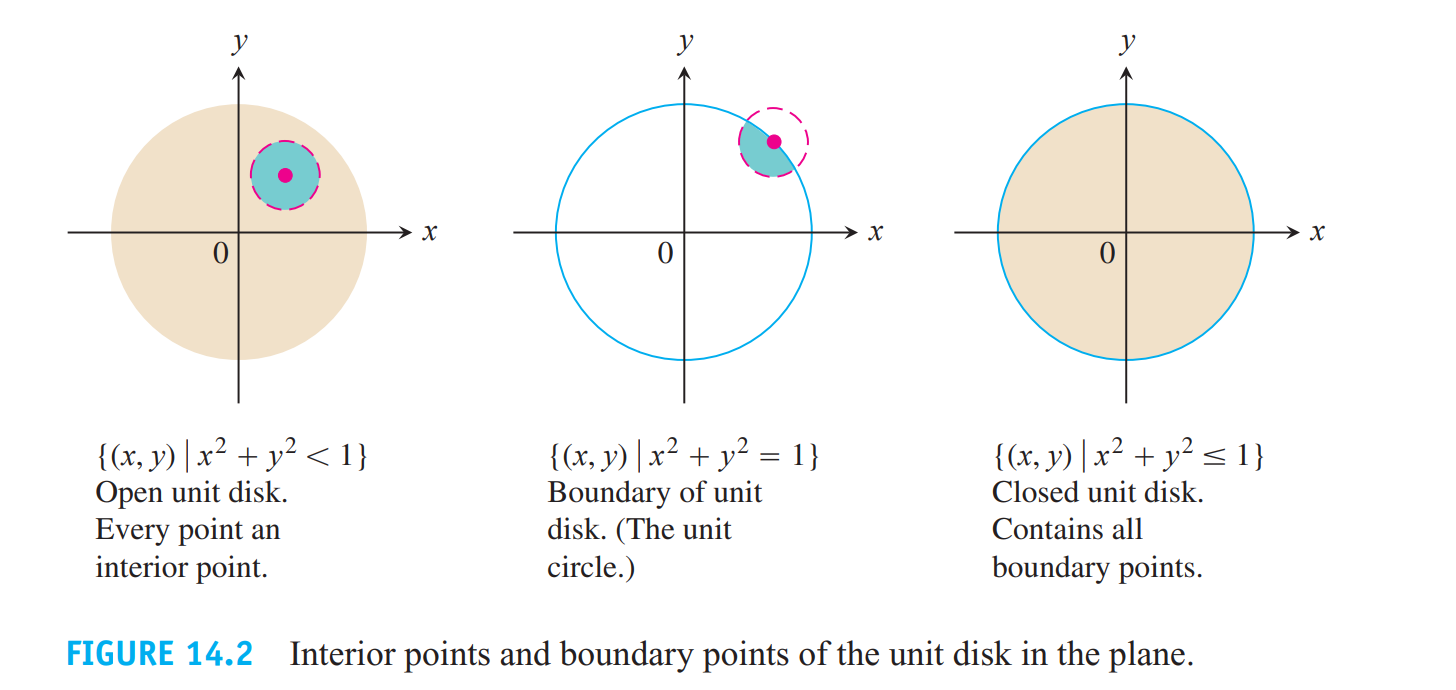
若存在$r>0$使得

$$R\subset U(O,r)$$

则为有界集

$y\ge x^2$为封闭无界集

满足$f(x,y)=c$的线为等值线(Level Curve)

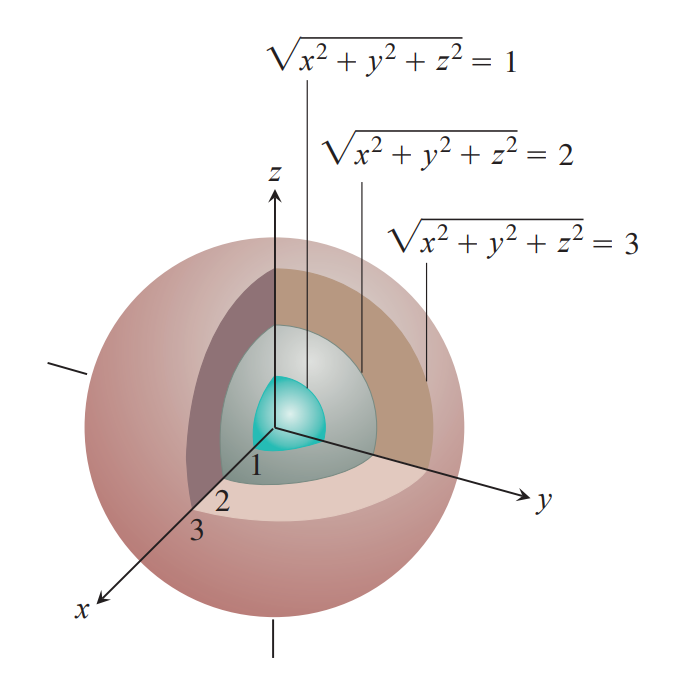
满足$f(x,y,z)=c$的面为等值面(Level Surface)

微分

偏导数

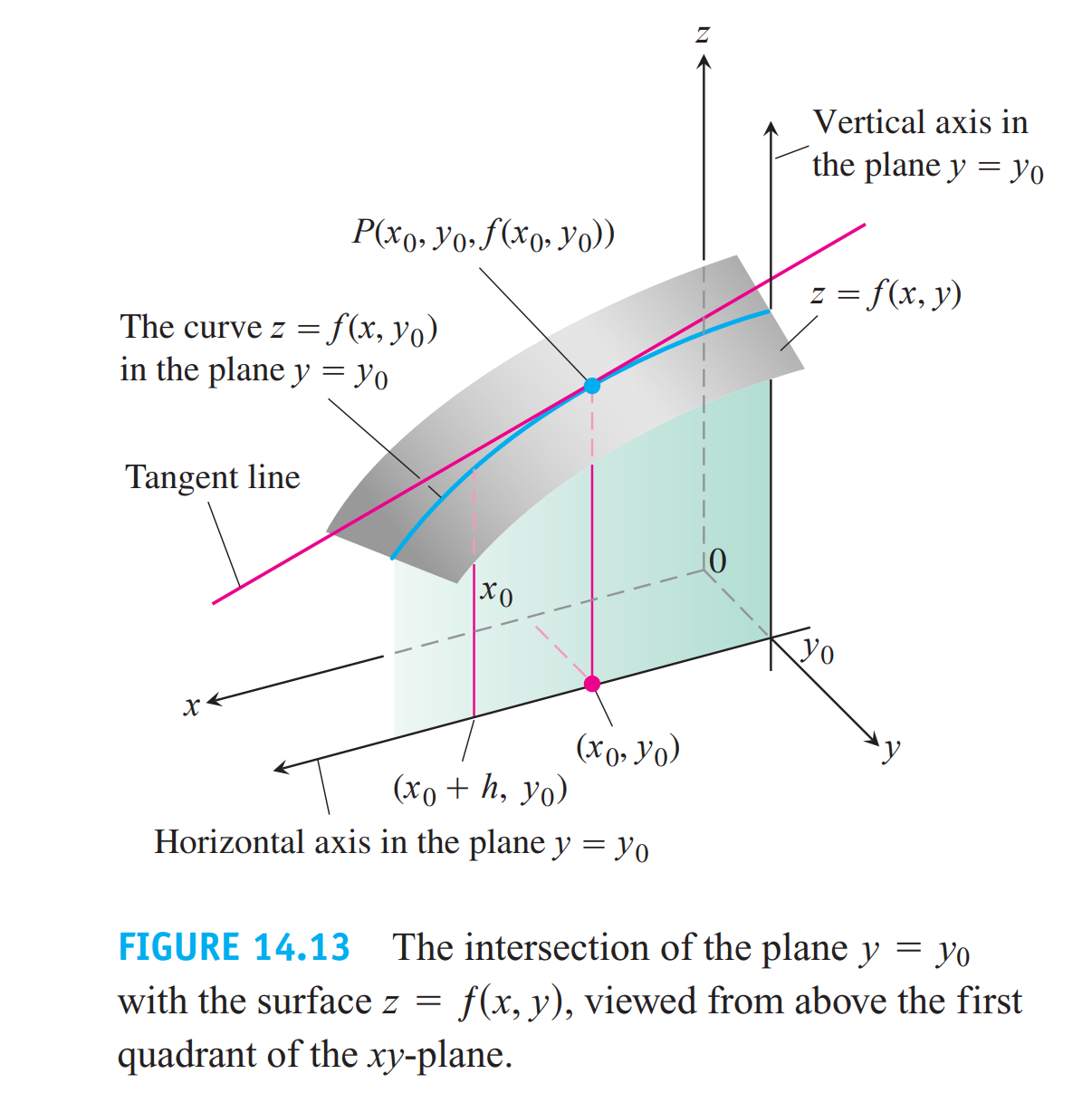
固定一个然后求导

To distinguish partial derivatives from ordinary derivatives we use the symbol $\partial$ rather than the $\text d$ previously used

$$\frac{\partial f}{\partial x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x, y_{0}\right)-f\left(x_{0}, y_{0}\right)}{\Delta x}$$

高阶

$$\frac{\partial^{2} f}{\partial x^{2}}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right), \quad \frac{\partial^{2} f}{\partial x \partial y}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)$$

杨氏定理(Young’s theorem)，二阶偏微分连续，二阶混合偏导数相等

$$\frac{\partial^{2} f}{\partial x \partial y}=\frac{\partial^{2} f}{\partial y \partial x}$$

可偏(有偏导数)不代表有全微分形式

全微分

$$\text{d}z=\frac{\partial f}{\partial x}\text{d}x+\frac{\partial f}{\partial y}\text{d}y$$

从而有标准线性近似

$$f(x,y)\approx f(x_0,y_0)+f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)=L(x,y)$$

对于误差$E(x,y)=f(x,y)-L(x,y)$

$$|E(x,y)|\le\frac12M(|x-x_0|+|y-y_0|)^2\\ M=\max\{|f_{xx}|,|f_{yy}|,|f_{xy}|\}$$

链式法则

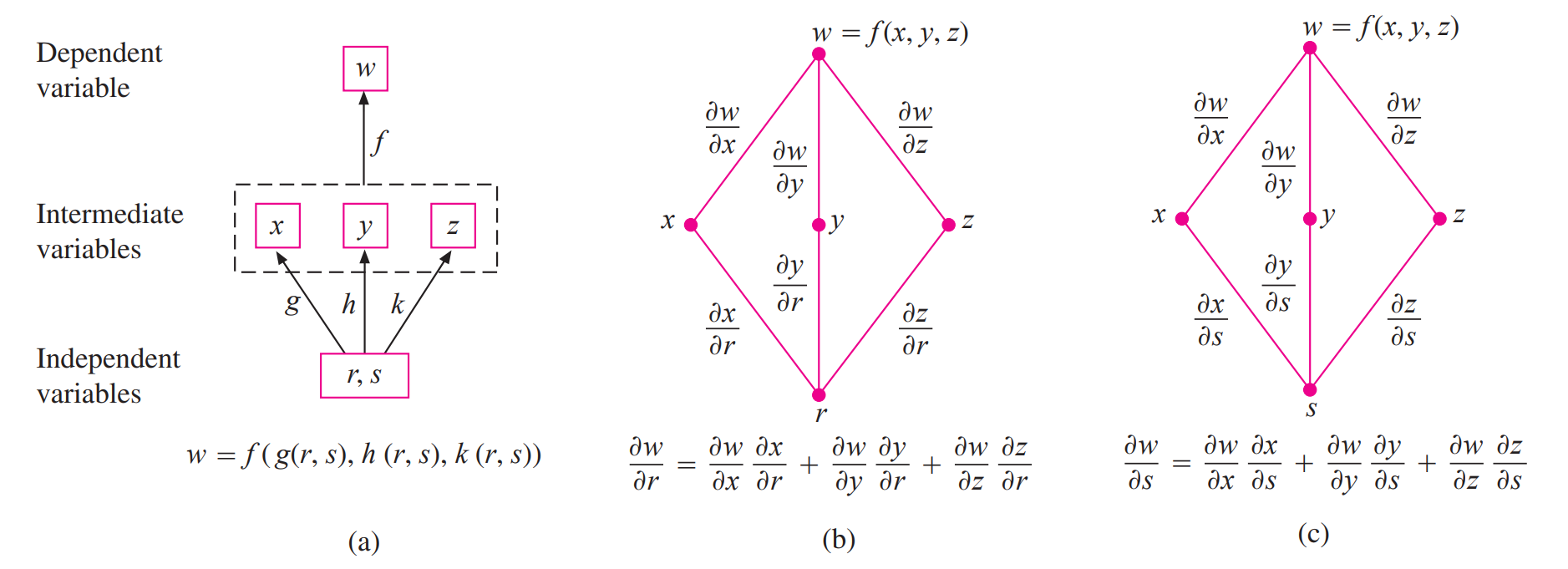
复合函数

$$x\overset{f_0 }{\rightarrow}x^1\to\cdots\overset{f_k }{\rightarrow}y\\ f=f_k^{\circ}f_{k-1}^{\circ}\dots^{\circ}f_0$$

利用全微分可以得到链式法则

$$w=f(x(t),y(t))\\ \frac{\partial w}{\partial t}=\frac{\partial f}{\partial x}\frac{\partial f}{\partial t}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial t}$$

更一般的

$$\frac{\partial w}{\partial r}=\frac{\partial w}{\partial x} \frac{\partial x}{\partial r}+\frac{\partial w}{\partial y} \frac{\partial y}{\partial r}+\frac{\partial w}{\partial z} \frac{\partial z}{\partial r} \\ \frac{\partial w}{\partial s}=\frac{\partial w}{\partial x} \frac{\partial x}{\partial s}+\frac{\partial w}{\partial y} \frac{\partial y}{\partial s}+\frac{\partial w}{\partial z} \frac{\partial z}{\partial s}$$

隐函数

首先，有方程

$$F(x,y,z)=0$$

从而若$F_z\ne 0$可以确定一个函数$z(x,y)$

由方程推导法(两边直接对$x,y$求导)

或用公式

$$\frac{\partial z}{\partial x}=-\frac{F_x}{F_z} \\ \frac{\partial z}{\partial y}=-\frac{F_y}{F_z}$$

利用全微分可以将两个导数同时求出

方程组

$$\begin{cases}F(x,y,u,v)=0\\ G(x,y,u,v)=0\end{cases}$$

如果

$$J=\frac{\partial(F,G)}{\partial(u,v)}=\begin{vmatrix}\frac{\partial F}{\partial u}&\frac{\partial F}{\partial v}\\\frac{\partial G}{\partial u}&\frac{\partial G}{\partial v}\end{vmatrix} \ne0$$

则可以确定$u(x,y)$和$v(x,y)$，一个方程确定一个因变量

将要求的因变量用自变量替换得到

$$\frac{\partial u}{\partial x}=-\frac1J\frac{\partial(F,G)}{\partial(x,v)}=-\frac1J\begin{vmatrix}\frac{\partial F}{\partial x}&\frac{\partial F}{\partial v}\\\frac{\partial G}{\partial x}&\frac{\partial G}{\partial v}\end{vmatrix}$$

同理也有方程推导法和微分法

根据克拉姆法则，对于一个$n$元线性方程组，如果它的系数矩阵的行列式不等于零，则可以使用如下公式求解：

$$x_i = \Delta_i / \Delta$$

其中，$x_i$是第$i$个未知数的值，$\Delta_i$是将系数矩阵中第$i$列替换为常数矩阵后的行列式值，$\Delta$是系数矩阵的行列式值。

方向导数

方向导数为函数在某一方向(正反都可以)上的变化率

$$\frac{\partial f}{\partial l}=\lim _{s \rightarrow 0} \frac{f\left(x_{0}+sl_x, y_{0}+sl_y\right)-f\left(x_{0}, y_{0}\right)}{s}$$

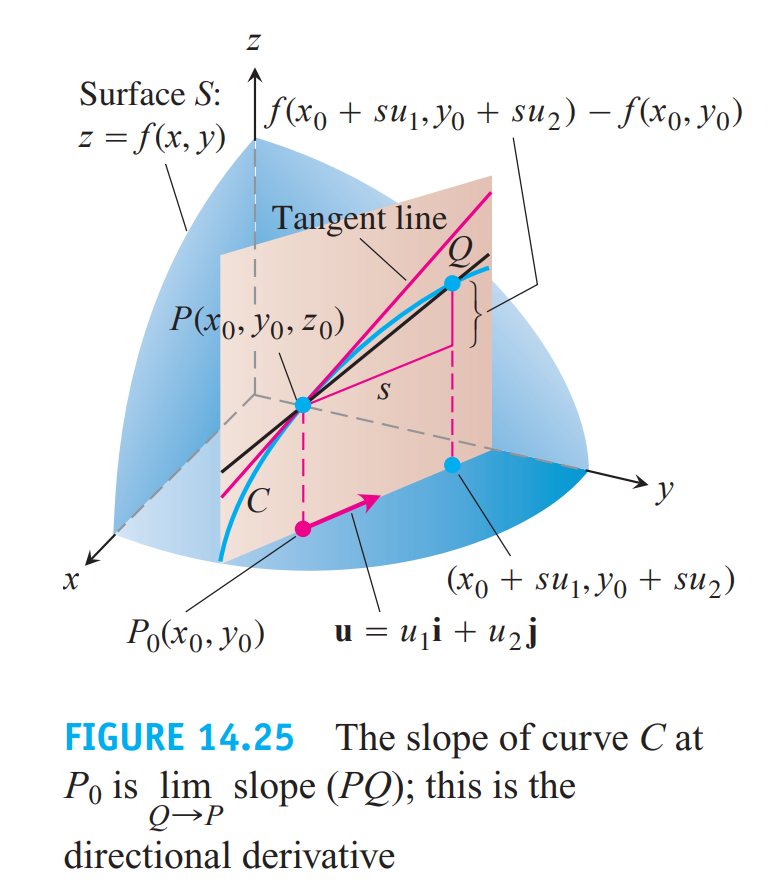
定义$l$的方向余弦为

$$\cos\alpha=\frac{\Delta x}{\Delta l},\cos\alpha=\frac{\Delta y}{\Delta l}$$

由全微分公式将导数沿方向分解，得到

$$\left. \frac{\partial f}{\partial l}\right|_{x_0,y_0}=\frac{\partial f}{\partial x}\cos\alpha+\frac{\partial f}{\partial y}\cos\beta\\ \text d f=(\nabla f\cdot \vec l)\text d s$$

梯度

定义梯度，Nabla算子

$$\text{grad}f=\nabla f(x,y)=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)$$

利用辅助角公式得出梯度方向的方向导数最大，或

$$\left. \frac{\partial f}{\partial l}\right|_{x_0,y_0}=\nabla f(x,y)\cdot(\cos\alpha,\cos\beta)$$

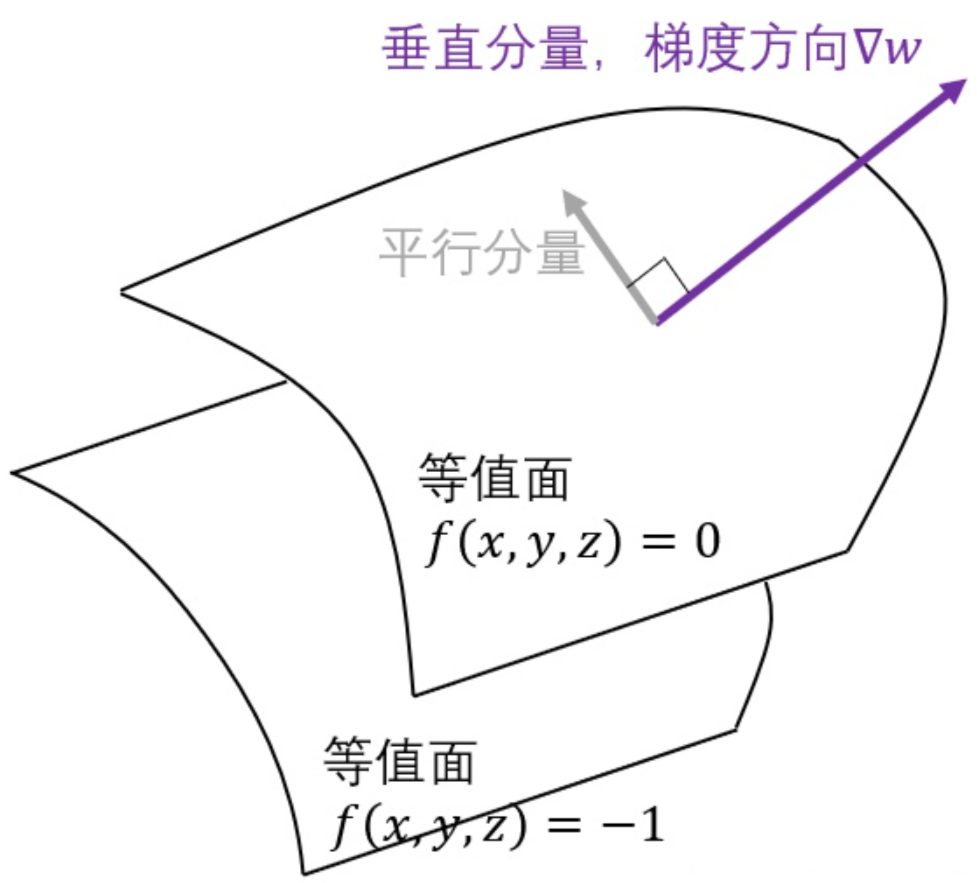
所以梯度指向上升最快的方向

可以看出梯度向量垂直于等高线的切线

$$\nabla (kf)=k\nabla f\\ \nabla(f\pm g)=\nabla f\pm \nabla g\\ \nabla (fg)=\nabla fg+f\nabla g\\ \nabla\left(\frac fg\right)=\frac{\nabla fg-f\nabla g}{g^2}$$

切线和法线

引入等值面$f(x,y)=c$，对于空间曲线引入参数$t$后得到

$$\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)\cdot\left(\frac{\partial x}{\partial t},\frac{\partial y}{\partial t}\right)=2 \frac{\partial f}{\partial t}=0$$

梯度向量垂直于等值面，梯度的模为沿梯度方向的方向导数

对于切线

$$\frac{x-x_0}{\varphi'(t_0)}=\frac{y-y_0}{\phi'(t_0)}=\frac{z-z_0}{\omega'(t_0)}$$

法平面为与切线垂直的面

$${\varphi'(t_0)}(x-x_0)={\phi'(t_0)}(y-y_0)={\omega'(t_0)}(z-z_0)$$

对于由方程确定的曲线

$$\begin{cases}F(x,y,z)=0\\ G(x,y,z)=0\end{cases}\\ J=\frac{\partial(F,G)}{\partial(y,z)}$$

则以$x$为参数可以写成

$$\begin{cases}x=x\\ y=y(x)\\z=z(x)\end{cases}$$

解出

$$T=(1,y_x,z_x)$$

整理得轮换对称式

$$T=\left(\begin{vmatrix}F_y&F_z\\ G_y& G_z\end{vmatrix}_M,\begin{vmatrix}F_z&F_x\\ G_z& G_x\end{vmatrix}_M,\begin{vmatrix}F_x&F_y\\ G_x& G_y\end{vmatrix}_M\right)$$

推广到三维空间，切向量

$$T=(F_x,F_y,F_z)=(-z_x,-z_y,1)$$

切平面

$$f_{x}\left(P_{0}\right)\left(x-x_{0}\right)+f_{y}\left(P_{0}\right)\left(y-y_{0}\right)+f_{z}\left(P_{0}\right)\left(z-z_{0}\right)=0$$

法线

$$x=x_{0}+f_{x}\left(P_{0}\right) t, \quad y=y_{0}+f_{y}\left(P_{0}\right) t, \quad z=z_{0}+f_{z}\left(P_{0}\right) t$$

可以方便地使用全微分公式得到

极值和最值

$n$ 元函数 $f(x_1,x_2,\ldots,x_n)$，若存在某个自变量取值的去心邻域，在该邻域内函数值不小于（或不大于）该自变量取值处的函数值，则称该自变量取值处为函数的极大值点（或极小值点）

必要条件

一阶偏导数都为$0$

$$f_x(x,y)=0,f_y(x,y)=0$$

充分条件

引入Hessian 矩阵

$$H=\begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n}\\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n}\\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}$$

对于二元

$$f_{xx}=A,f_{xy}=B,f_{yy}=C$$

若$AC-B^2>0$则有极值，$A/C>0$则为极小值

若$AC-B^2<0$则无极值，$AC-B^2=0$则可能有

拉格朗日函数

对于约束条件$g(x_1,x_2,\dots,x_n)=0$，可以构造拉格朗日函数 $L(x_1,x_2,\dots,x_n)=f(x_1,x_2,\dots,x_n)+\lambda g(x_1,x_2,\dots,x_n)$

$$\begin{cases} \frac{\partial L}{\partial x_1} = 0\\ \frac{\partial L}{\partial x_2} = 0\\ \cdots\\ \frac{\partial L}{\partial x_n} = 0\\ \frac{\partial L}{\partial \lambda} = 0\\ \end{cases}$$

需要注意的是，拉格朗日乘数法并不适用于所有类型的优化问题，有些问题可能存在多个局部极小值或不可导等情况，需要根据具体问题进行分析

前置知识

克罗内克函数

Kronecker Delta符号

$$\delta_{ij} =\{ 1,\text{if}\; i = j\;;\;0,\text{if}\; i ≠ j \}$$

爱因斯坦求和约定

当式子中任何一个指标出现了==两次==，那么该式表示的实际上是对这个角标一切可能值的求和，如

$$C_{ij}=A_{ik}B_{kj}$$

$k$出现了两次，表示对$ k $进行了求和

$$\sum a_ib_i=a_ib_i$$

出现两处的指标称为哑标(dummy index)，出现一次指标称为自由指标(特指)

对于上下标需要一起算

$$a_i^i=\sum a_i^i$$

等式两边自由指标的数量要相同

列维-奇维塔符号

(Levi-Civita symbol)也称为epsilon符号或完全反对称符号

$$\varepsilon_{ijk}=\begin{cases}1\quad ijk=123或偶次交换\\ -1\quad ijk=123经奇数次交换\\ 0 \quad 有两个指标相同 \end{cases}$$

由此三阶行列式可以表示成

$$\begin{vmatrix} a_1& a_2 & a_3\\ b_1& b_2 & b_3 \\ c_1& c_2 & c_3 \end{vmatrix}=\varepsilon_{ijk}a_ib_jc_k$$

三维情况

$$\vec{a}\cdot \vec{b}=a_ib_j\\ \vec{a}\times \vec{b}=\vec{e_i}\varepsilon_{ijk}a_jb_k\\ (\vec{a}\times \vec{b})_i=\varepsilon_{ijk}a_jb_k$$

函数

标量

$$\varphi(\vec{x})$$

矢量

$$\vec{A}(\vec{x})=A_1\vec{e_1}+A_2\vec{e_2}+A_3\vec{e_3}$$

算子

哈密顿算子

$$\nabla=\begin{bmatrix}\frac{\partial }{\partial x_1} \frac{\partial}{\partial x_2} \cdots \frac{\partial }{\partial x_n}\end{bmatrix}=\vec{e_i}\frac{\partial }{\partial x_i}$$

方向导数

$$\frac{\partial u}{\partial \vec s}=\lim_{\Delta\vec s\to0}\frac{f(\vec r+\Delta\vec s)-f(\vec r)}{\Delta\vec s}$$

方向导数最大为梯度方向

$$\nabla u\cdot \text d \vec s=\text du$$

是在$\text d \vec s$方向上的微分变化

$\nabla u$指的是梯度场

散度

对于曲面$\Sigma$，向量场的通量表示为

$$\Phi=\int_\Sigma \vec A\cdot \text d\vec \sigma$$

从而有

$$\text{div} \vec A=\lim_{V\to 0}\frac1V\int_{\partial V}\vec A\cdot \text d\vec \sigma$$

$\partial V$代表$V$的边界，散度代表单位体积的通量

$$\text{div}\vec A=\nabla\cdot \vec A\\ \lim_{\Delta V\to 0}(\nabla\cdot \vec A)\cdot \Delta V=\int_{\partial (\Delta V)}\vec A\cdot \text d\vec \sigma$$

两端积分得到散度定理

$$\int_V(\nabla\cdot \vec A)\text d V=\int_{\partial V}\vec A\cdot \text d\vec \sigma$$

说明体积内的散度为边界上的通量

引入

考虑复变函数$w(t)$

$$w(t) = u(t) + \text iv(t)$$

对其求导得到

$$w'(t) = u'(t) + \text iv'(t)\\ \frac{\text d} {\text dt }e^{z_0t}=z_0e^{z_0t}$$

同理，有

$$\int_a^bw(t)\text dt=\int_a^bu(t)\text dt+\text i\int_a^bv(t)\text dt$$

从而我们可以分别对实部和虚部进行积分

$$\Re\int_a^bw(t)\text dt=\int_a^b\Re [w(t)]\text dt\\ \Im\int_a^bw(t)\text dt=\int_a^b\Im [w(t)]\text dt$$

所以微积分基本定理也可以使用

$$\left.{\int_a^bw(t)\text dt=W(t)}\right|_a^b$$

如

$$\int_0^{\frac\pi 4}e^{\text it}\text dt=\frac{\sqrt 2}2+\left(1-\frac{\sqrt 2}2\right)\text i$$

注意，如积分中值定理不适用于复变函数

曲线

$$z(t) = x(t) + \text iy(t)\quad (t\in[a,b])$$

这就是曲线$C$的方程

• 若$z$值没有重复相交则为简单曲线(simple arc)
• 只有$z(a)=z(b)$则称为简单封闭曲线(simple closed curve)

弧微分

$$\text d s=\sqrt{1+y'^2}\text dx=\sqrt{[x'(t)]^2+[y'(t)]^2}\text d t$$

所以弧长

$$L=\int_a^b\sqrt{[x'(t)]^2+[y'(t)]^2}\text d t$$

对于$\varphi’(\tau)>0$，也可变换

$$Z(t)=z(\varphi(t))$$

又因为

$$|z'(t)|=\sqrt{[x'(t)]^2+[y'(t)]^2}\\ L=\int_\alpha^\beta|z'(\varphi(t))|\varphi'(t)\text d t=\int_\alpha^\beta|Z'(t)|\text d t$$

考虑径矢

$$\mathbf{T}=\frac{z'(t)}{|z'(t)|}$$

如果$z’(t)$连续且$\ne0$，即$x’(t),y’(t)$不同时为$0$

则曲线处处有切线可以自由转动，则曲线光滑

轮廓

contour通常指的是复平面上的曲线，它可以用于描述复变函数在复平面上的取值和变化情况，用两种方式定义

1. 参数方程：$z (t)$，其中 $t$ 是在某个区间 $[a,b]$ 上变化的实数。通过让 $t$ 在区间 $[a,b]$ 上遍历，我们就可以得到一条曲线
2. 等值线方程：$f(z) = c$，其中 $c$ 是一个常数。这个方程表示的是函数 $f(z)$ 在复平面上取值为 $c$ 的所有点

积分

对于一个轮廓$C$，积分表示为

$$\int_Cf(z)\text dz\;\;\text{or}\;\;\int_{z_1}^{z_2}f(z)\text dz$$

对于由参数定义的$C$

$$\int_Cf(z)\text dz=\int_Cf[z(t)]z'(t)\text dt$$

性质

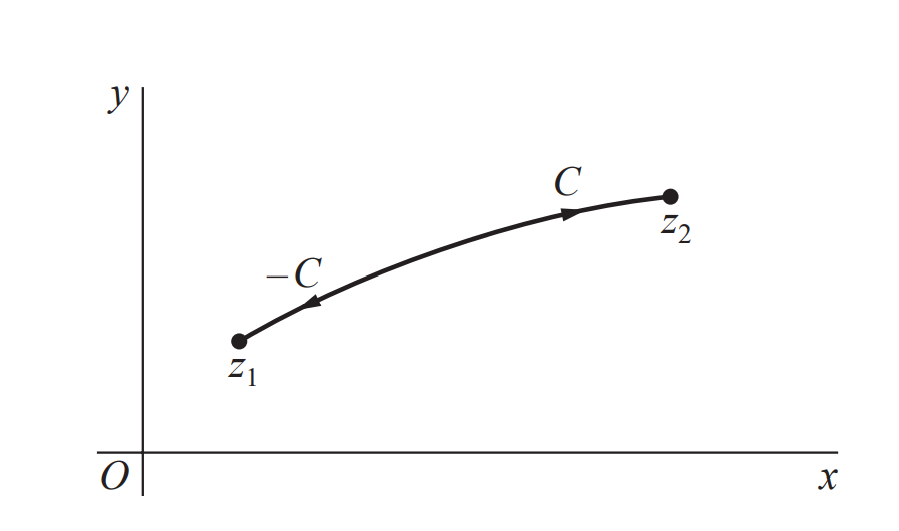
对于方向相反的轮廓$z(-t)$

$$\int_{-C}f(z)\text dz=-\int_Cf(z)\text dz$$

可加性

$$\int_Cf(z)\text dz=\int_{C_1}f(z)\text dz+\int_{C_2}f(z)\text dz$$

概念

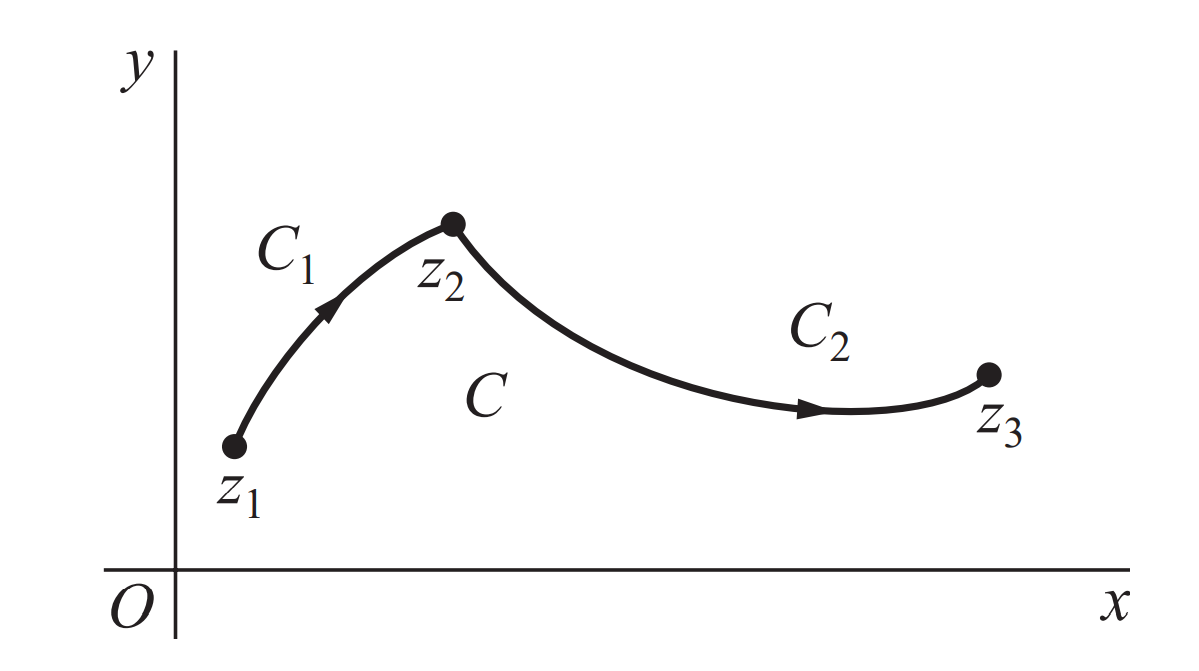
类比一般函数复变函数就是将一个复数映射成另外一个复数

$$w=f(z)\\ u+v\text{i}=f(x+y\text{i})\\ f(z)=u(x,y)+v(x,y)\text{i}=f(re^{\text{i}\theta})$$

如平方根

$$f(z)=\sqrt{r}\exp\left(\frac{\theta}2\text{i}\right)$$

相较于定义在实数域上的函数，复变函数没有图像

从变换的角度来思考，函数将平面上的每一个点映射到了另外一个点

例如反射，旋转等变换

可视化

通过对于特殊曲线的变换来可视化

$$f(z)=z^2\\ \begin{cases}u=x^2-y^2\\ v=2xy\end{cases}$$

$$e^z=e^{x+y\text{i}}=e^xe^{y\text{i}}$$

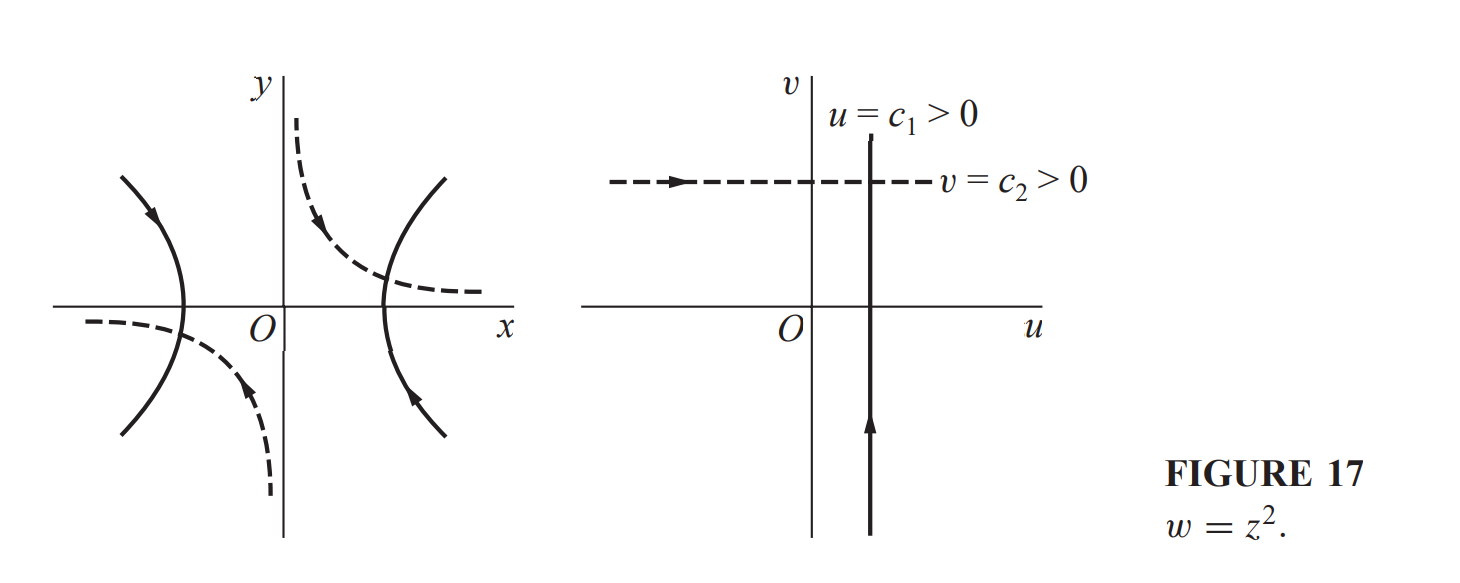
通过指数形式也可表示变换

极限

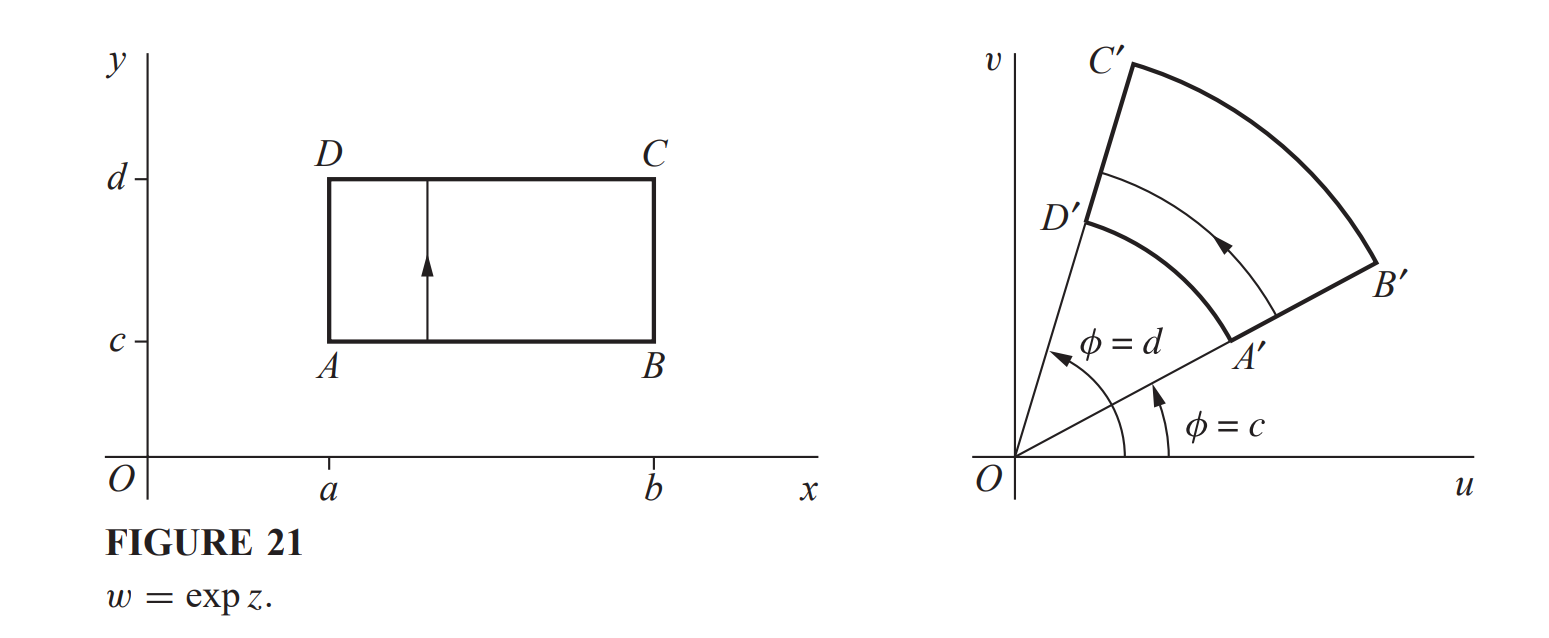
函数极限

对于任意$\epsilon>0$都有$\delta>0$使得$0<|x-x_0|<\delta$有$|f(x)-A|<\epsilon$

类比

对于任意$\epsilon>0$都有$\delta>0$使得$0<|z-z_0|<\delta$有$|f(z)-w_0|<\epsilon$

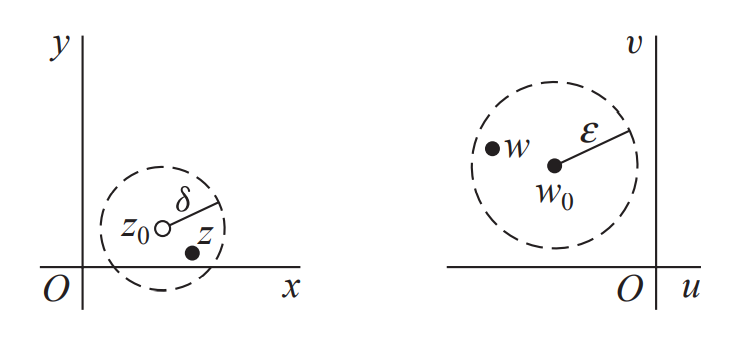
则记为

$$\lim_{z\to z_00}f(z)=w_0$$

定理

$$\lim_{z\to z_0}f(z)=w_0\Leftrightarrow\begin{cases}\displaystyle\lim_{(x,y)\to(x_0,y_0)}u(x,y)=u_0\\ \displaystyle\lim_{(x,y)\to(x_0,y_0)}v(x,y)=v_0\end{cases}$$

利用这个定理可以很方便地将复变函数的极限转换为一般函数极限

所以四则运算法则同一般函数极限的运算法则

没有所谓左右极限的概念

无穷

将无穷远点(point at infinity)引入复平面，得到扩充复平面

全体复数再加上一个无穷远点构成扩充复数

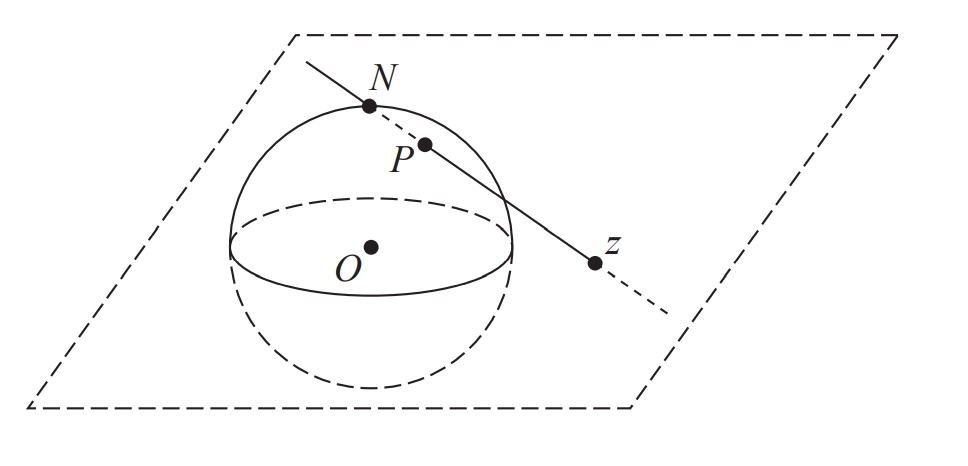
引入黎曼球面，球面投影点$z$为复平面上的点，和球面上的$P$一一对应

加上无穷远点$N$代表无穷远点，构成了球和复数的对应关系

可以通过倒数来将极限转化为0

$$\lim_{z\to \infty}f(z)=\infty\Leftrightarrow \lim_{z\to 0}\frac1{f(1/z)}=0$$

连续

定义为

1. $\displaystyle \lim_{z\to z_0}f(z)$存在
2. $f(z_0)$存在
3. $\displaystyle \lim_{z\to z_0}f(z)=f(z_0)$

同理有若两函数都连续则$f(g(x))$也连续

如果函数在某一封闭区域内连续那么

$$|f(z)|\le M$$

导数

$$f'(z_0)=\lim_{\Delta z\to0}\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}$$

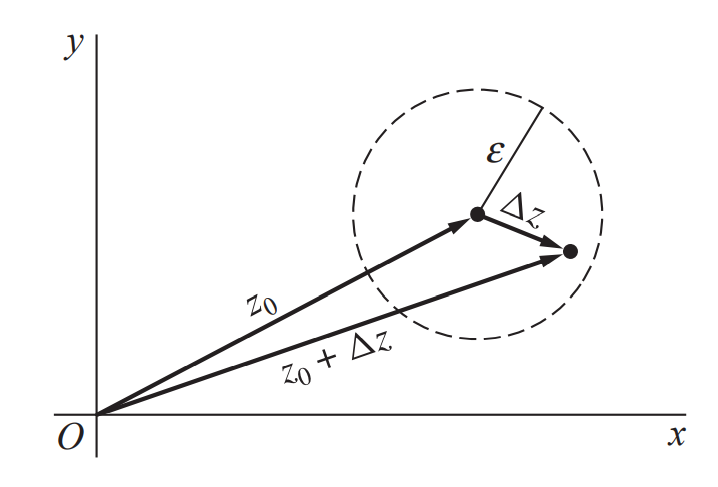
导数的大部分公式都可以用于复变函数，但复变函数自变量为二维，所以趋向有方向

但因为导数定义，不同趋向极限应该相同，得到可导的必要条件

$$\begin{cases}\displaystyle\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\\ \displaystyle\frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}\end{cases}$$

这就是柯西-黎曼方程(Cauchy–Riemann Equations)

$$f'(z_0)=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\text{i}$$

导数还可以用极坐标来表示

$$\\f'(z)=f'(re^{\theta\text{i}})=u(r,\theta)+v(r,\theta)\text{i}$$ $$\begin{cases}ru_r=v_\theta\\ u_\theta=-rv_r\end{cases}\\ f'(z_0)=e^{-\theta\text{i}}(u_r+v_r\text i)$$

解析函数

某区域上处处可微分的复变函数

If we should speak of a function $f$ that is analytic in a set $S$ which is not open, it is to be understood that $f$ is analytic in an open set containing $S$

如果$f’(z)=0$在$D$上恒成立则$f(z)$在$D$上是常函数

调和函数

有二阶导数同时满足拉普拉斯方程

$$\frac{\partial^2 f}{\partial x_1^2}+\frac{\partial^2 f}{\partial x_2^2}+\cdots+\frac{\partial^2 f}{\partial x_n^2}=0$$

对于复变函数，如果在$D$上是解析函数，则两个分量$u,v$是调和函数

特殊函数

指数函数$e^z$运算法则符合一般指数的运算

$$\frac{\text{d}}{\text{d}z}e^z=e^z\\ e^{z+2n\pi\text{i}}=e^z$$

对数函数

$$\ln z=\ln r+\text{i}(\Theta+2n\pi)\\ \Theta=\text{Arg } z$$

对应多个值，如果我们限定主枝(principal branch)

$$\ln z=\ln r+\text i\Theta\quad(\Theta\in(-\pi,\pi))$$

不能取等否则不连续，一般$\log z\Leftrightarrow\ln z$

$$\log z_1z_2=\log z_1+\log z_2\\ \log \left (\frac{z_1}{z_2}\right )=\log z_1-\log z_2\\ z^n=e^{n\log z}$$

$n$可以为复数，即指数为复数

三角函数

利用欧拉公式，利用共轭复数得到

$$\sin z=\frac{e^{\text i z}-e^{-\text i z}}{2\text i}\\ \cos z =\frac{e^{\text i z}+e^{-\text i z}}{2\text i}$$

许多性质和三角函数一模一样

$$\frac{\text d} {\text dz }\sin z=\cos z\\ \sin(z_1 + z_2) = \sin z_1 \cos z_2 + \cos z_1 \sin z_2\\ \sin ^2z+\cos ^2z=1$$

对于双曲函数

$$\sinh z=\frac{e^z-e^{-z}}2\\ \cosh z=\frac{e^z+e^{-z}}2\\ \sin(\text iz)=\text i\sinh z\\ \cos(\text iz)=\sinh z$$

复数

表示

$$z=a+b\text{i}\\ a=\Re z\quad b=\Im z$$ $$|z|=|a+b\mathrm{i}|=\sqrt{a^2+b^2}\\\overline{z}=a-b\text{i}$$

其中$\overline{z}$为共轭复数

$$\Re z=\frac12(z+\overline z)\\ \Re z=\frac1{2\text i}(z-\overline z)\\$$

运算定律

$$(a+b\mathrm{i})\pm (c+d\mathrm{i})=(a\pm c)+(b\pm d)\mathrm{i}\\(a+b\mathrm{i})(c+d\mathrm{i})=(ac-bd)+(ad+bc)\mathrm{i}\\\frac{a+b\mathrm{i} }{c+d\mathrm{i} }=\frac{(a+b\mathrm{i})(c-d\mathrm{i})}{(c+d\mathrm{i})(c-d\mathrm{i})}=\frac{(ac+bd)+(bc-ad)\mathrm{i} }{c^2+d^2}$$

性质

$$z\overline z=|z|^2\\ \overline{z+w}=\overline z+\overline w\\ \overline{zw}=\overline z\;\overline w\\ |zw|=|z||w|\\ \left|\frac{z}{w}\right|=\frac{|z|}{|w|}$$

几何表示

$$z = a + b\text{i} = r(\cos \theta + \text{isin}\theta ) = re^{\theta{\text i} }$$

其中$\theta $称为辐角，记为$\text{Arg} z$，对于$-\pi<\theta\le\pi$

$$\text{Arg} z=\text{arg}z+2k\pi,k \in \mathbf{Z}$$

而$\text{arg}z$就是辐角的主值

性质

$$z_{1} z_{2}=r_{1} r_{2}\left(\cos \left(\theta_{1}+\theta_{2}\right)+i \operatorname{isin}\left(\theta_{1}+\theta_{2}\right)\right)\\ \text{Arg}(z_{1} z_{2})=\text{Arg}z_{1}+\text{Arg}z_{2}$$

同理

$$\frac{z_{1}}{z_{2}}= \frac{r_{1}}{r_{2}}\left[\cos \left(\theta_{1}-\theta_{2}\right)+\operatorname{isin}\left(\theta_{1}-\theta_{2}\right)\right]\\ \operatorname{Arg}\left(\frac{z_{1}}{z_{2}}\right)=\operatorname{Arg} z_{1}-\operatorname{Arg} z_{2}$$

可以看出复数乘除和旋转有关

应用于垂直，有

$$\operatorname{arg}\left(\frac{z_{1}}{z_{2}}\right)=\pm\frac\pi2\\ \Re\frac{z_{1}}{z_{2}}=\Re\frac{z_{1}}{z_{2}}|z_2|^2=\Re z_1\overline{z_2}=0$$

同理，平行

$$\operatorname{arg}\left(\frac{z_{1}}{z_{2}}\right)=0/\pi\\\Im z_1\overline{z_2}=0$$

棣莫弗公式

de Moivre formula

$$(\cos \theta+\text{i} \sin \theta)^{n}=\cos n \theta+\text{i} \sin n \theta=(e^{\text{i} \theta})^n$$

从而对于$|z|=1$

$$\omega=\sqrt[n]{z},\omega^n=z\\\cos n \varphi+\text{i} \sin n \varphi=\cos \theta+\text{i} \sin \theta\\ \varphi=\frac{\theta+2k\pi}{n}\;(k=0,1,\cdots ,n-1)$$

注意到每次加上$2\pi/n$

$$\omega_n=\cos \frac{2 \pi}{n}+i \sin \frac{2 \pi}{n}\\ \sqrt[n]1=\omega_n^0,\omega_n^1,\omega_n^2\dots\omega_n^{n-1}$$

这就是$n$个单位根，$\omega_n$为主$n$次单位根

不难想到可以利用这$n$个值来表示多项式

引入

远距作用

过去人们认为相距一段距离的物体发生相互作用是一种远距作用(action at a distance)

它不需要中间介质的传递只需要两个物体就能发生

但很多现象无法解释例如为什么有的时候只有直接接触才能产生力

场论

因此后来人们认为两个相距一段距离的物体之间存在一种物质通过连续的相互作用使作用得到传递，人们把它称之为场

作用在场中的传递就像力在弹簧中的传递一样

标量场

$$f(x,y,z)$$

空间中的每一个点都对应一个标量

固定一个分量可以使用等高线来表示

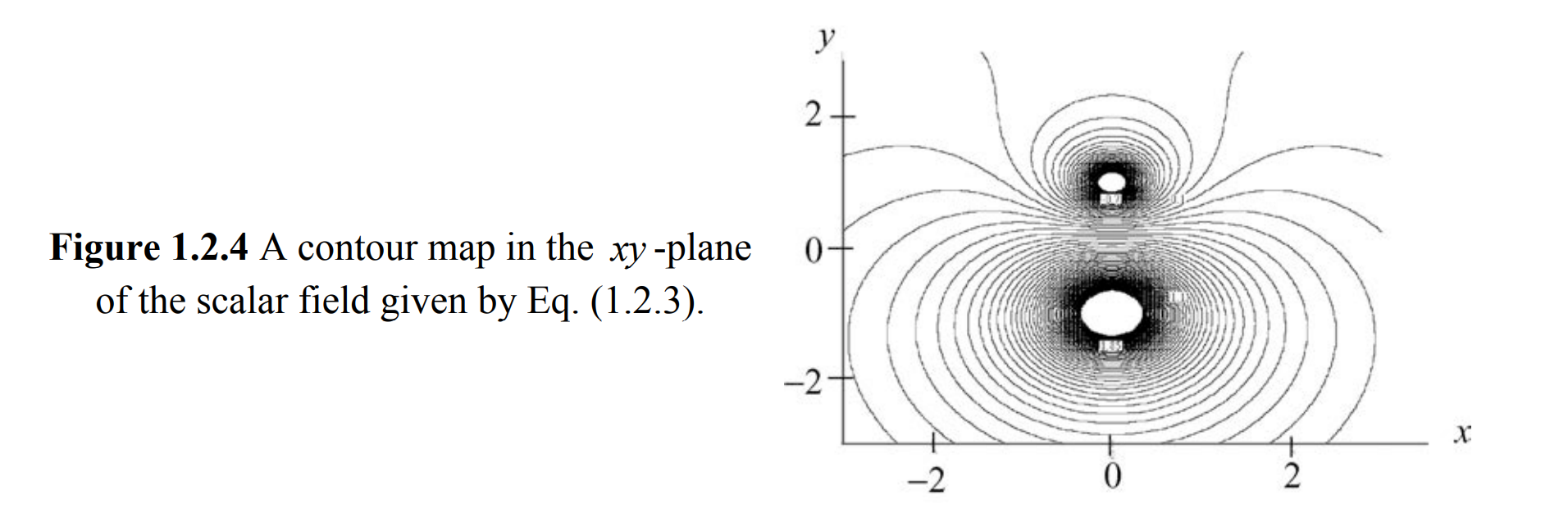
还可以使用颜色映射或三维地形图(Relief Maps)来表示

向量场

结果为向量

$$\vec{F}(x,y,z)=f_x(x,y,z)\mathbf{i}+f_y(x,y,z)\mathbf{j}+f_z(x,y,z)\mathbf{k}$$

流场

$$\overrightarrow{\mathbf{v}}(x, y, z)=v_{x}(x, y, z) \hat{\mathbf{i}}+v_{y}(x, y, z) \hat{\mathbf{j}}+v_{z}(x, y, z) \hat{\mathbf{k}}$$

电场中很多的概念是从流场中类比而来的

重力场

$$\vec{g}=-G\frac{M}{r^2}\hat{\mathbf{r}}$$

电场

由库仑定律得到

$$\vec{F}_e=k_e\frac{Qq}{r^2}\hat{\mathbf r},\vec{E}_e=k_e\frac{Q}{r^2}\hat{\mathbf r}\\ k_e=\frac1{4\pi\varepsilon _0}$$

注意电荷有正负

$$\vec{F}_e=q\vec{E}_e$$

对于场强，由微元法

$$\text d\vec{E}_e=k_e\frac{\text dQ}{r^2}\hat{\mathbf r}\\$$

积分

$$\vec{E}_e=k_e\int_V\frac{\text dQ}{r^2}\hat{\boldsymbol r}\\ \text dQ=\lambda\text{d}x= \sigma\text{d}S= \rho\text{d}V$$

磁场

在周围放置许多小磁针，由于力矩的作用使得小磁针成如下排列

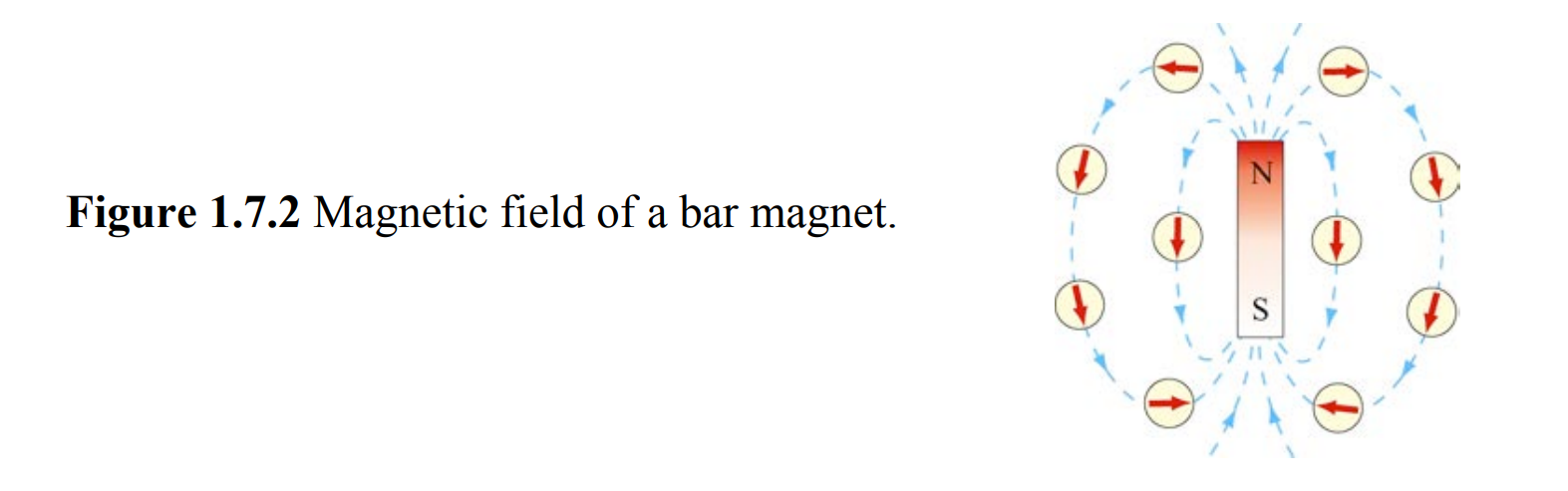
这形成的一根根线被法拉第描述成电场线

电场线的切线代表该点处的场强方向

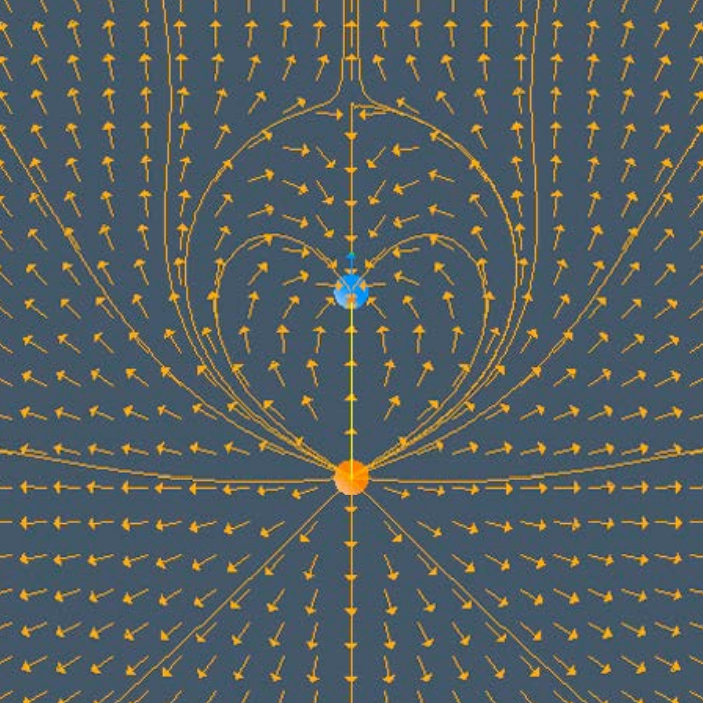
Faraday called the field lines for electric field “lines of force.”

运动的电荷产生磁场(电生磁)

高斯定理

电通量

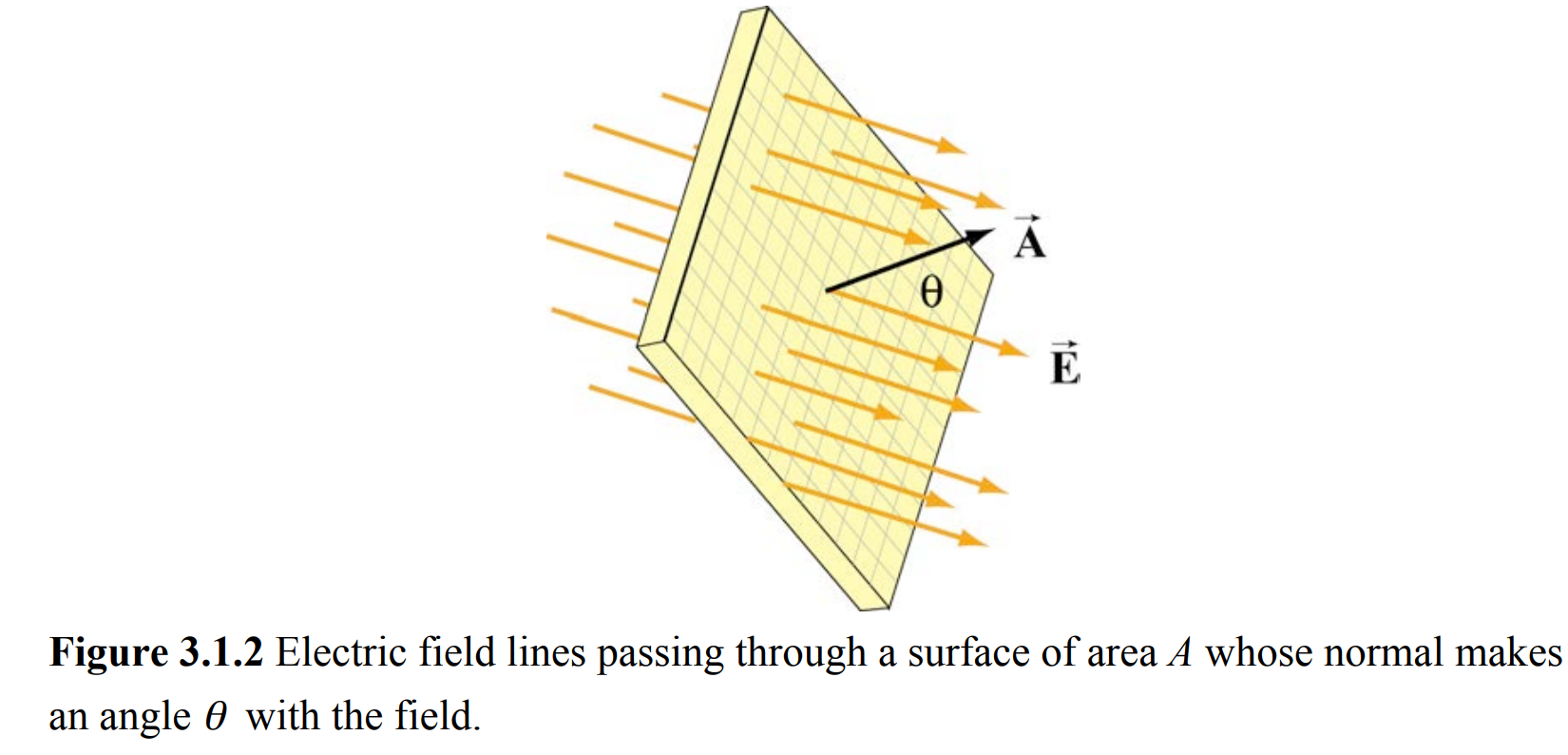
用电通量来描述穿过某一面积的电场线条数

$$\Phi=\vec E\cdot \vec S$$

利用点电荷的电通量公式可以导出

$$\Phi_e=\frac{q}{\varepsilon_0}$$

库仑力满足平方反比关系，故有高斯定理

$$\Phi=\oint_{S}\vec E\cdot \text d\vec S=\frac1{\varepsilon_0}\sum_{i=1}^nq_i$$

应用

如果选取恰当的高斯面(球面或柱面)，则

$$E,\cos \theta=\text{constant}$$

就可以通过电荷量计算出场强

无限长的导线

$$E=\frac\lambda{4\pi\varepsilon_0 r}(\cos\theta_1-\cos\theta_2)\\ E=\frac\lambda{2\pi\varepsilon_0 r}$$

无限大平板

$$E=\frac{\sigma}{2\varepsilon_0 }$$

对电偶极子，$p=ql$由负到正

$$E=\frac{-p}{4\pi\varepsilon_0r^3}$$

电势能

电场力为保守力，做功与路径无关

$$W_{ab}=\frac{q_0}{4\pi\varepsilon_0}\sum_iq_i\left(\frac1{r_{ia}}-\frac1{r_{ib}}\right)$$

所以有环路定理

$$\oint_lE\cdot\text dl=0$$

电场力对应一种势能

$$\Delta V_{e}=-\int_{A}^{B}\left(\overrightarrow{\mathbf{F}}_{e} / q_{t}\right) \cdot \text d \overrightarrow{\mathbf{s}}=-\int_{A}^{B} \overrightarrow{\mathbf{E}} \cdot \text d \overrightarrow{\mathbf{s}},\\ \Delta U=q_t\Delta V_e$$

故有保守力做功等于势能的减少量

$$\Delta U=-W_e\\ \Delta V = \Delta V_{CA} + \Delta V_{BC}$$

对于点电荷

$$\Delta E=E_{B}-E_{A}=-\int_{A}^{B} \frac{Q}{4 \pi \varepsilon_{0} r^{2}} \text d r=\frac{Q}{4 \pi \varepsilon_{0}}\left(\frac{1}{r_{B}}-\frac{1}{r_{A}}\right)$$

As in the case of gravity, only the difference in electrical potential is physically meaningful, and one may choose a reference point and set the potential there to be zero. In practice, it is often convenient to choose the reference point to be at infinity, so that the electric potential at a point P becomes

$$V_p=\int_p^\infty\overrightarrow{\mathbf{E}} \cdot \text d \overrightarrow{\mathbf{s}},\quad V_\infty=0\\ V = k_e\frac Q r$$

点乘，所以考虑梯度

$$E=-\nabla V=-\left(\frac{\partial V}{\partial x},\frac{\partial V}{\partial y},\frac{\partial V}{\partial z}\right)$$

更严谨的

$$\text dV=\frac{\partial V}{\partial x}\text dx+\frac{\partial V}{\partial y}\text dy+\frac{\partial V}{\partial z}\text dz\\ \text dV=-E\cdot \text d s$$

导体的电场

静电平衡

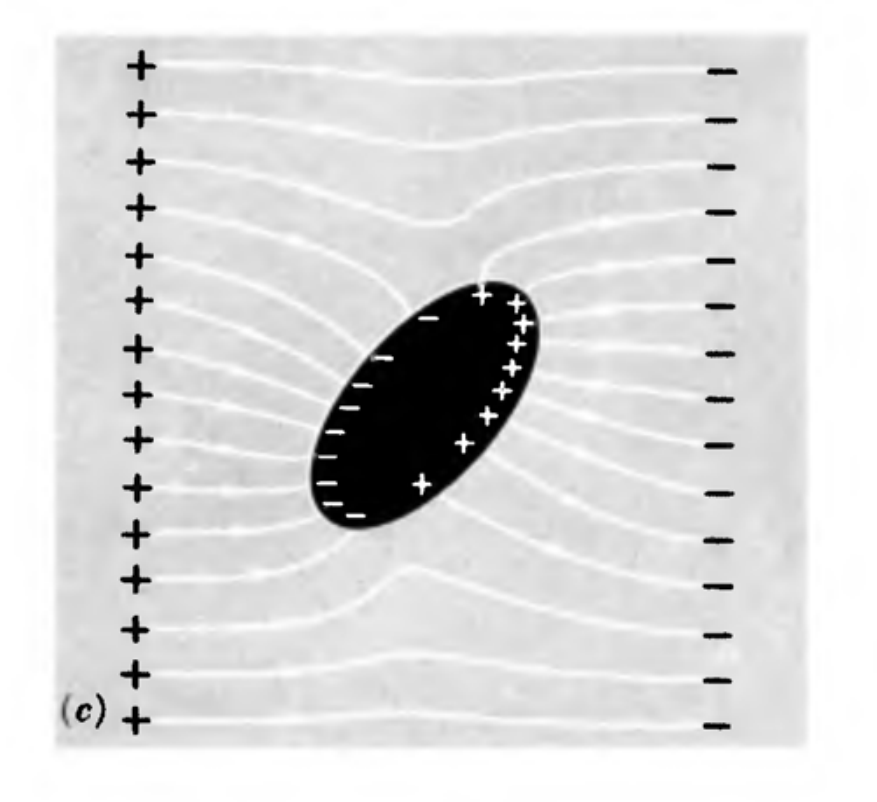
对于导体内部，条件为

$$E+E_{感}=0$$

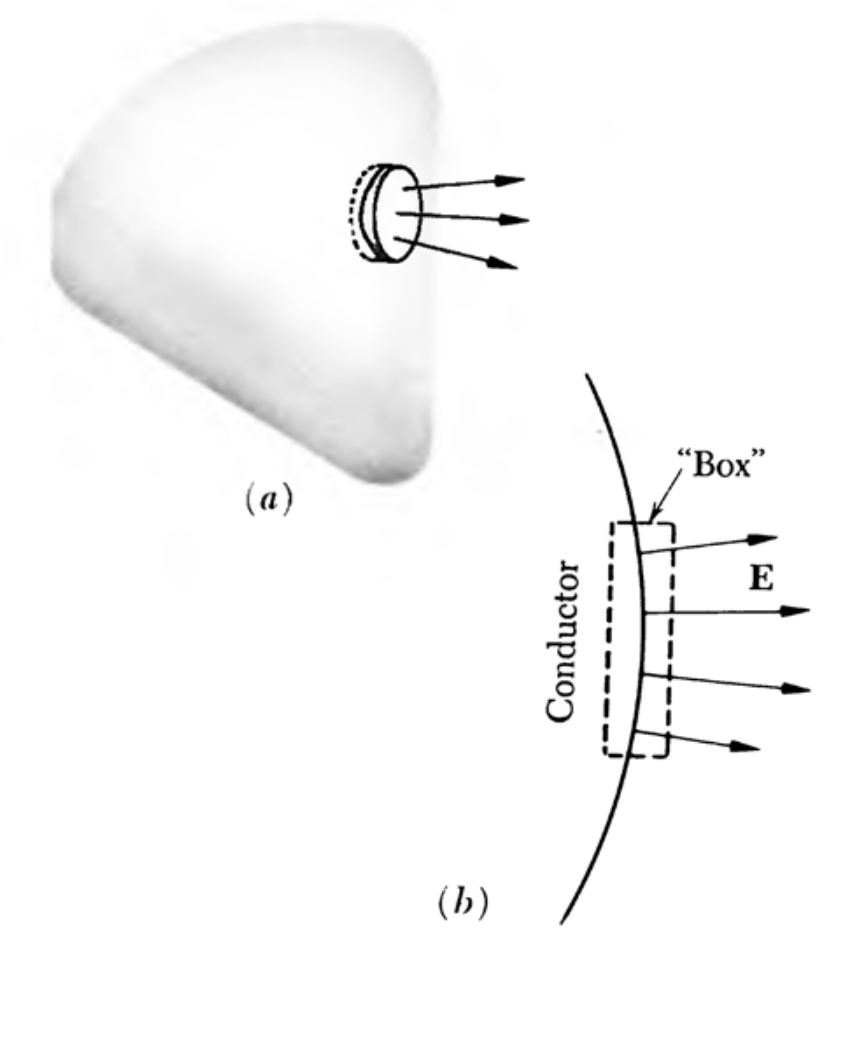
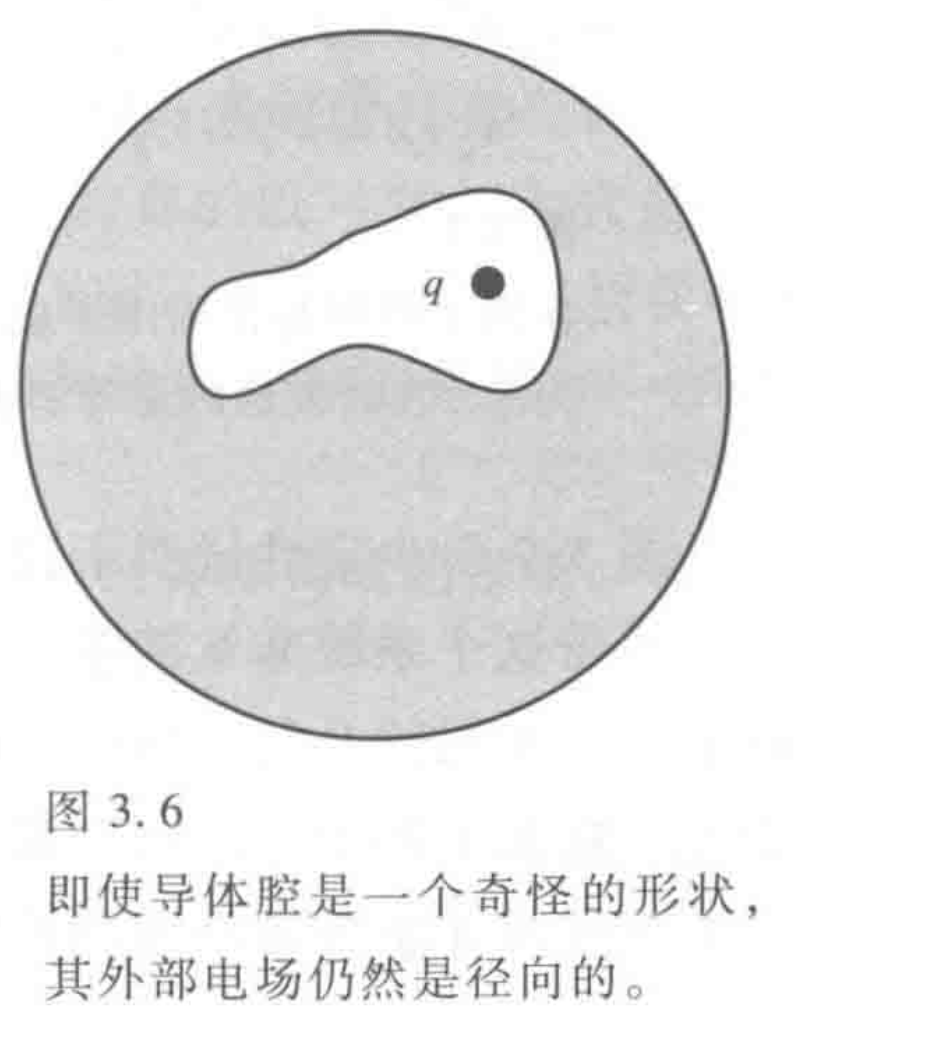
对表面用高斯定理得到若内部没有电荷则电荷只能在表面分布

对于表面电场(区分于内部)

$$E=\frac \sigma{\varepsilon_0}$$

对于内部有电荷的情况，内外不会相互影响

内部电荷为$-q$，外层分布只和外电场有关

若接地则为静电屏蔽，没有电场

电介质

因为电介质常为中性存在正负电荷所以引入电偶极子和偶极矩(电矩)

$$\vec p=q\vec l$$

方向由负电荷指向正电荷

电介质中存在大量电偶极子，所以引入电极化强度

$$\boldsymbol P=\frac{ \sum_i\boldsymbol p_i }V$$

对于表面，有

$$\sigma'=P\cos\theta =P_n$$

高斯定理

单独对极化电荷

$$\oint_{S}\vec P\cdot \text d\vec S=-\sum_{i}q_{i}$$

为了方便计算单独考虑自由电荷产生的电场

$$\oint_{S}(\varepsilon_0E+P)\cdot \text d\vec S=-\sum_{\text{free}}q_{i}$$

从而定义电位移

$$D=\varepsilon_0E+P\\ E=\frac{D-P}{\varepsilon_0}$$

合场强是由自由电荷和极化电荷产生电场的叠加

类比电场线我们可以引入电位移线，始于正自由电荷终于负自由电荷

对于各向同性的电介质，$\chi _e$为电极化率

$$P=\chi _e\varepsilon_0E\\ D=(1+\chi _e)\varepsilon_0E=\varepsilon_r\varepsilon_0E=\varepsilon E$$

将$\varepsilon$称为为电介质的介电常量，$\varepsilon_r$为相对介电常量

电容器

电容为电容器容纳电荷的本领

$$C=\frac{Q}V$$

单位为法拉

$$\rm 1 F=10^6\mu F=10^{12}pF$$

常见电容器

平行板电容器

$$C=\frac{\varepsilon_r\varepsilon_0S}{d}$$

将$\varepsilon$称为为电容率，$\varepsilon_r$为相对电容率

球型

$$C=\frac{4\pi \varepsilon R_A R_B}{ R_B-R_A}$$

圆柱

$$C=\frac{2\pi\varepsilon l}{\ln\frac{R_B}{R_A}}$$

连接

和电阻相反

串联

$$\frac1C=\sum_i\frac1{C_i}$$

并联

$$C=\sum_i C_i$$

静电场的能量

电荷之间相互作用从而存在能量，类比引力势能

$$W_e=\frac12\sum_iq_iV_i$$

对于连续分布的带电体

$$W_e=\frac12\int_qV\text dq$$

电容器

由于电容器的$U$为电势差，充电时电荷从一个极板移向另一个极板

$$W=\frac12QU=\frac 12CU^2=\frac12\frac{Q^2}C$$

所以从广义上讲，电场的能量就是聚集电荷所需的功

$$W_e=\int _V\frac 12\varepsilon E^2\text dV$$

其中$\frac 12\varepsilon E^2$为电场的能量密度

空间直角坐标系

记为$[O;\boldsymbol i,\boldsymbol j,\boldsymbol k]$，若为右手系，则有

$$\boldsymbol i\times \boldsymbol j=\boldsymbol k$$

坐标表示

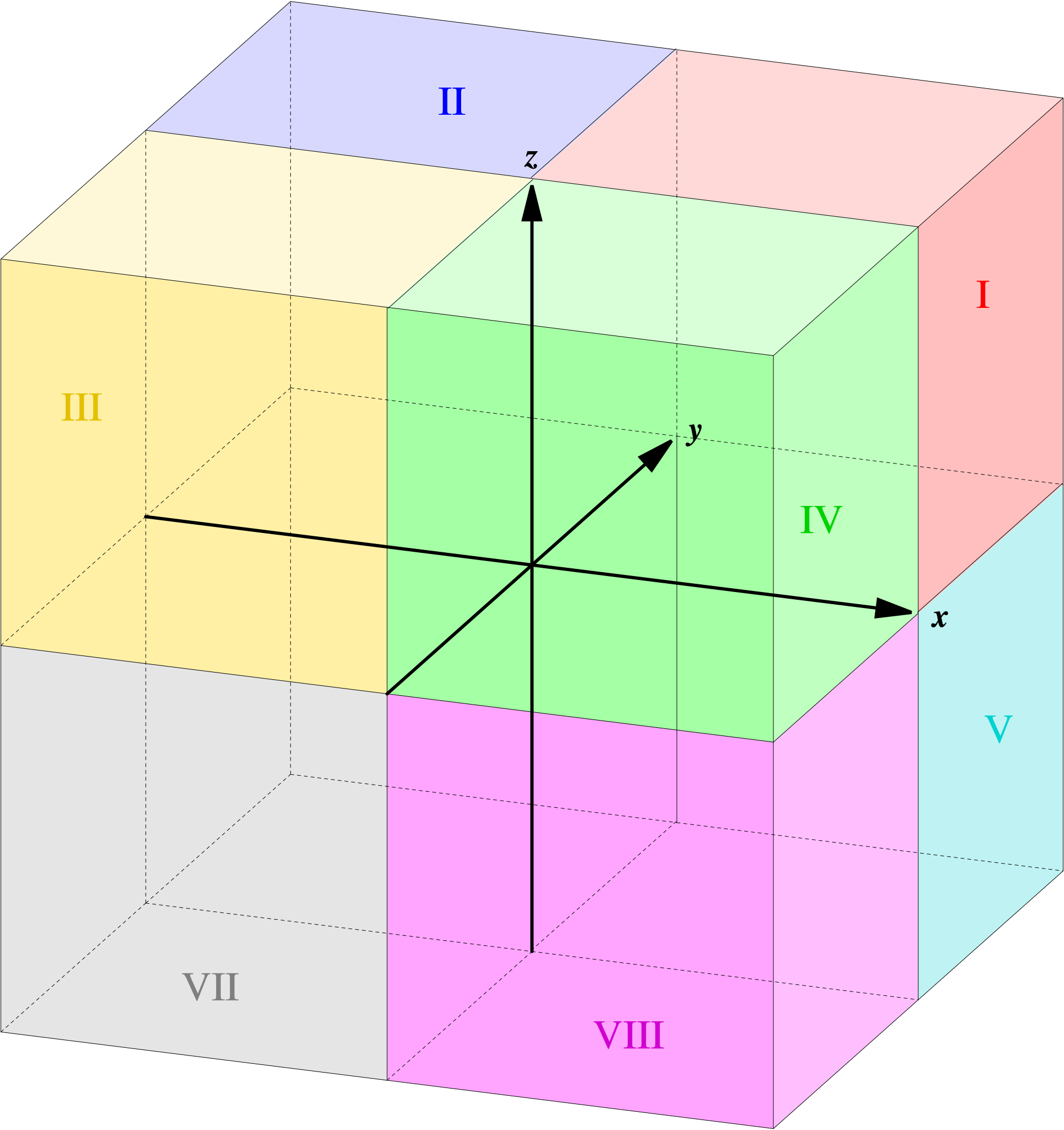
$xOy$面从上面和从下面看，分为八个卦限
任意向量可以分解为

$$\boldsymbol r=x\boldsymbol i+y\boldsymbol j+z\boldsymbol k\\ \boldsymbol r=(x,y,z)$$

定比分点

$$\vec{AM}=\lambda\vec{MB}\\ \vec{OM}=\left(\frac{x_1+\lambda x_2}{1+\lambda},\frac{y_1+\lambda y_2}{1+\lambda},\frac{z_1+\lambda z_2}{1+\lambda}\right)$$

方向角

$$|\vec{OM}|=\sqrt{x^2+y^2+z^2}\\ \cos\alpha=\frac{x}{|\vec{OM}|},(\alpha\to x)\\\beta\to y,\gamma\to z$$

分别为方向角和方向余弦

$$\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$$

具体应用

直线

$$\vec{OR}=\vec{OA}+t\vec{AR}\quad(t\in \mathbf{R})\\ \mathbf p=f(t)$$

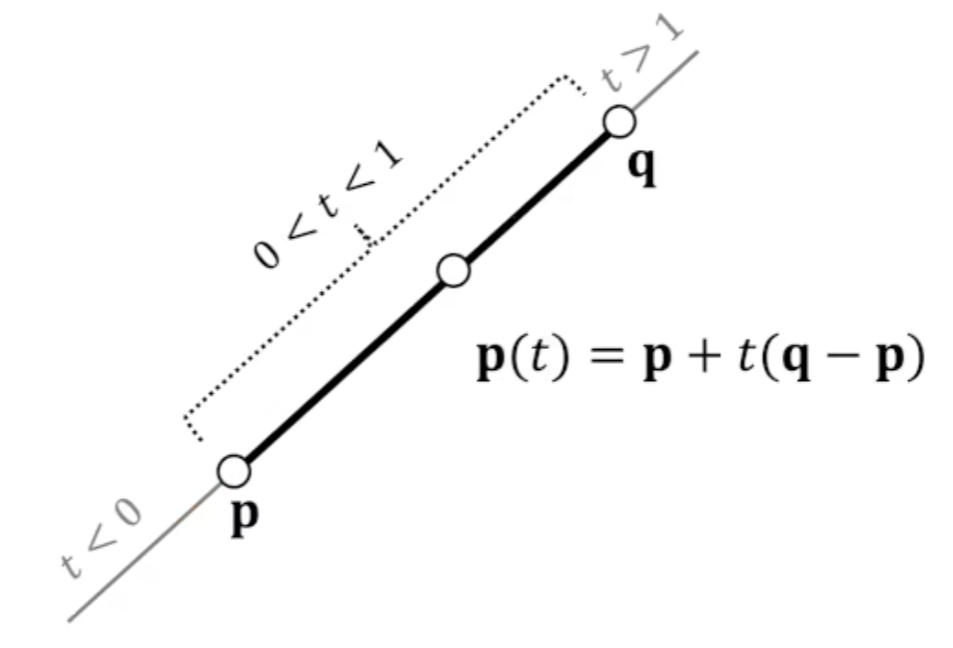
射线$t\ge 0$，线段$t\in[0,1]$

$$f(x,y)=Ax+By+C=0$$

$(A,-B)/(-A,B)$为方向向量

平面直线的两点式

$$(y_0-y_1)x+(x_1-x_0)y+x_0y_1-x_1y_0=0$$

从而$(a,b)$到直线的距离为

$$\text{signed distance}=\frac{f(a,b)}{\sqrt{A^2+B^2}}$$

三维空间中的直线的坐标表示为

$$(x,y,z)=(x_0,y_0,z_0)+vt\\ \frac{x-x_0}{v_1}=\frac{y-y_0}{v_2}=\frac{z-z_0}{v_3}$$

同理可以用两个平面的交线来表示

$$\begin{cases}A_1x+B_1y+C_1z+D_1=0\\A_2x+B_2y+C_2z+D_2=0\end{cases}$$

这就是平面的一般方程

点乘

平面

点在平面的哪

$$s=\vec{CP}\cdot \boldsymbol n=0$$

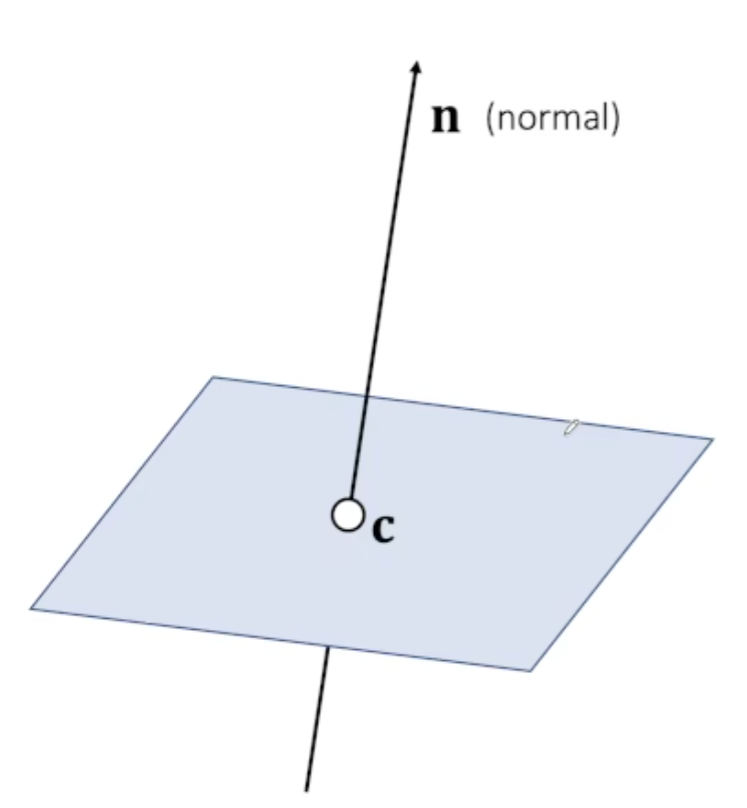
$s>0$在平面上，反之在平面下(先定义方向向量)

考虑直线和平面的夹角

$$\sin \theta=|\cos <\mathbf s,\mathbf n>|$$

平面的点法式方程

$$A(x-x_c)+B(y-y_c)+C(z-z_c)=0\\ f(x,y)=Ax+By+C$$

截距式方程

$$\frac xa+\frac yb+\frac zc=1x$$

距离

$$\text{distance}=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}$$

投影

$$\text{Prj}_{\vec{OM}}\vec{OA}=\frac{\vec{OM}\cdot \vec{OA}}{|\vec{OM}|}$$

结果为一个数，有正负

$$s=(\boldsymbol q-\boldsymbol o)^T\overline{\boldsymbol v}$$

叉乘

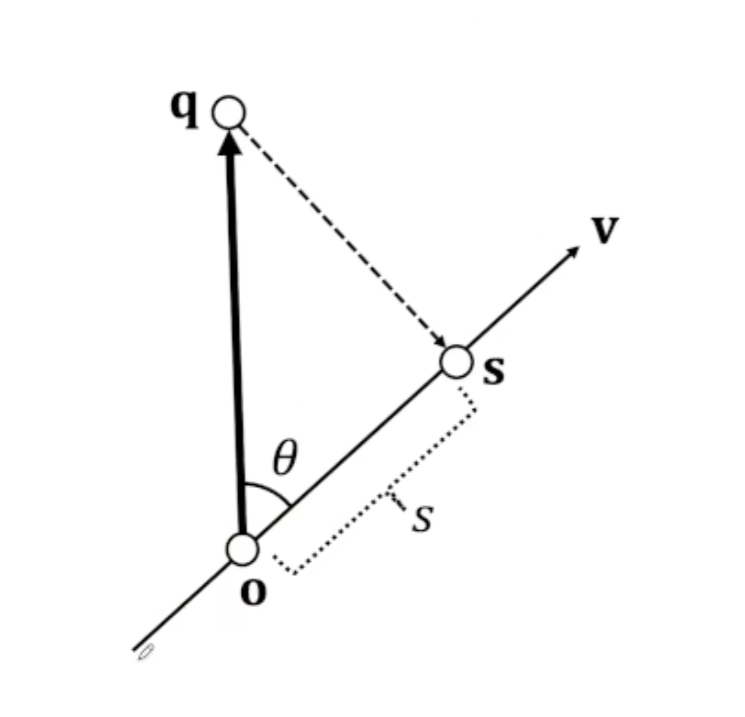
平行共线

$$\vec{a} \times \vec{b}=\vec{0}$$

则$\sin \theta=0$，同向或反向

面积

$$S=\frac12||(\boldsymbol{x_1-x_0})\times(\boldsymbol{x_2-x_0})||\\ \boldsymbol{n}=\boldsymbol{x_{10}}\times\boldsymbol{x_{20}}/||\boldsymbol{x_{10}}\times\boldsymbol{x_{20}}||$$

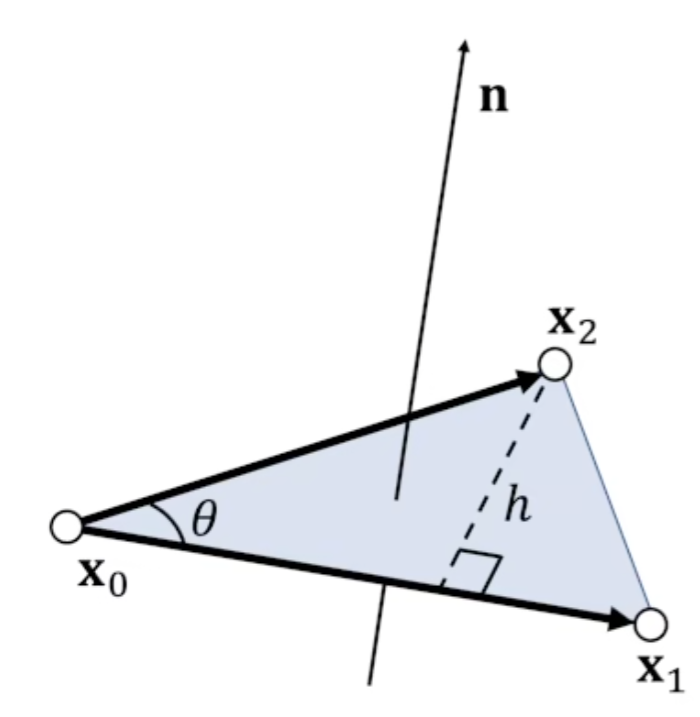
拓扑关系很重要，否则法向量相反

是否在三角形内

$$\vec{PA}\times\vec{PB},\vec{PB}\times\vec{PC},\vec{PC}\times\vec{PA}$$

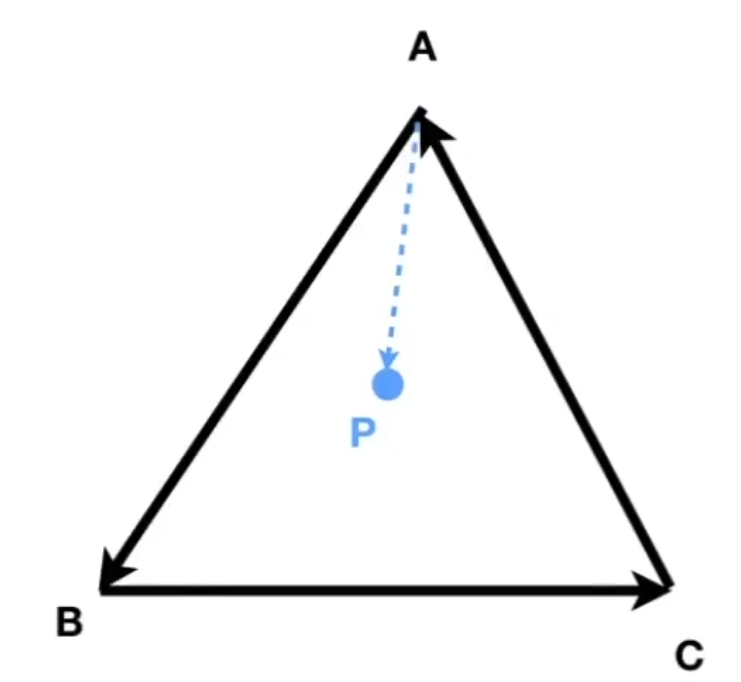
三个值同号，一半为三个三角形的有向面积

混合积

$$\begin{array}{l} V&=\frac{1}{3} h A=\frac16\mathbf{x}_{10}\times \mathbf{x}_{20}\cdot\mathbf{x}_{30}\\ &=\frac{1}{6}\left|\begin{array}{cccc} \mathbf{x}_{1} & \mathbf{x}_{2} & \mathbf{x}_{3} & \mathbf{x}_{0} \\ 1 & 1 & 1 & 1 \end{array}\right| \\ \end{array}$$

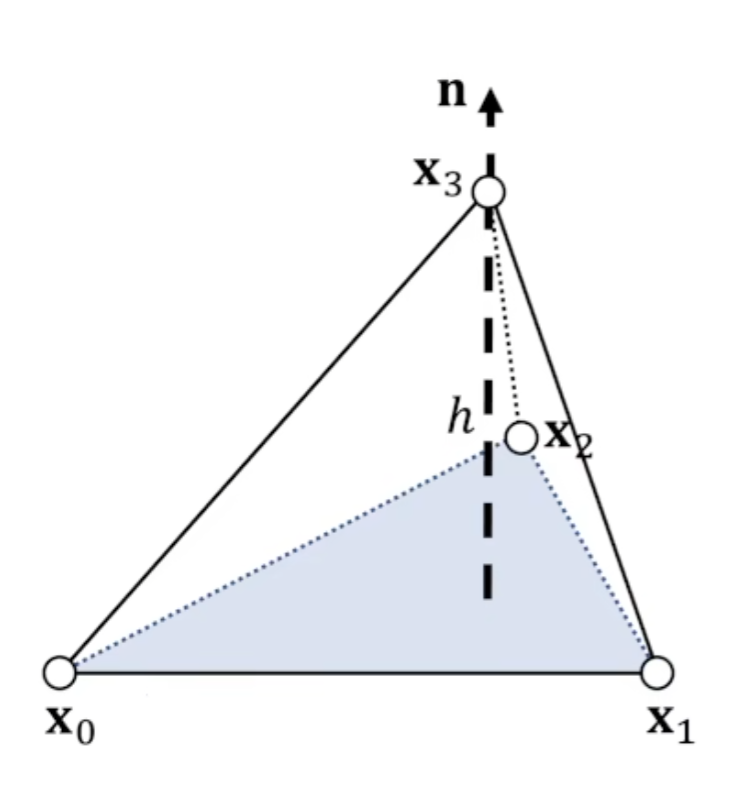
$\mathbf{x}_{3} $在平面以上则为正体积

体积为$0$则说明$\mathbf{x}_{3} $在平面上

曲面

用三元函数来表示

$$f(x,y,z)=0$$

这种表示可以非常方便地判断一个点是否在面上

一般使用向量来表示

$$\mathbf p=(x,y,z)\\ f(\mathbf p)=0$$

类比定义梯度

$$\mathbf n=\nabla f(\mathbf p)=\left(\frac{\partial f(\mathbf p)}{\partial x},\frac{\partial f(\mathbf p)}{\partial y},\frac{\partial f(\mathbf p)}{\partial z}\right)$$

切平面

$$(\mathbf p-\mathbf a)((\mathbf a-\mathbf b)\times(\mathbf a-\mathbf c))=0$$

球面

$$f(\mathbf p)=(\mathbf p-\mathbf c)^2-r^2=0$$

旋转曲面

绕哪个轴旋转哪个不变

例如母线在$yOz$上，则绕$y$轴旋转的方程为

$$f(y,\pm\sqrt{x^2+z^2})$$

若要还原母线则关键看$x^2+z^2$

柱面

平面曲线叫做准线，直线叫做母线

对于二维$f(x,y)=0$表示平面曲线

而对于三维空间表示柱面

二次曲面

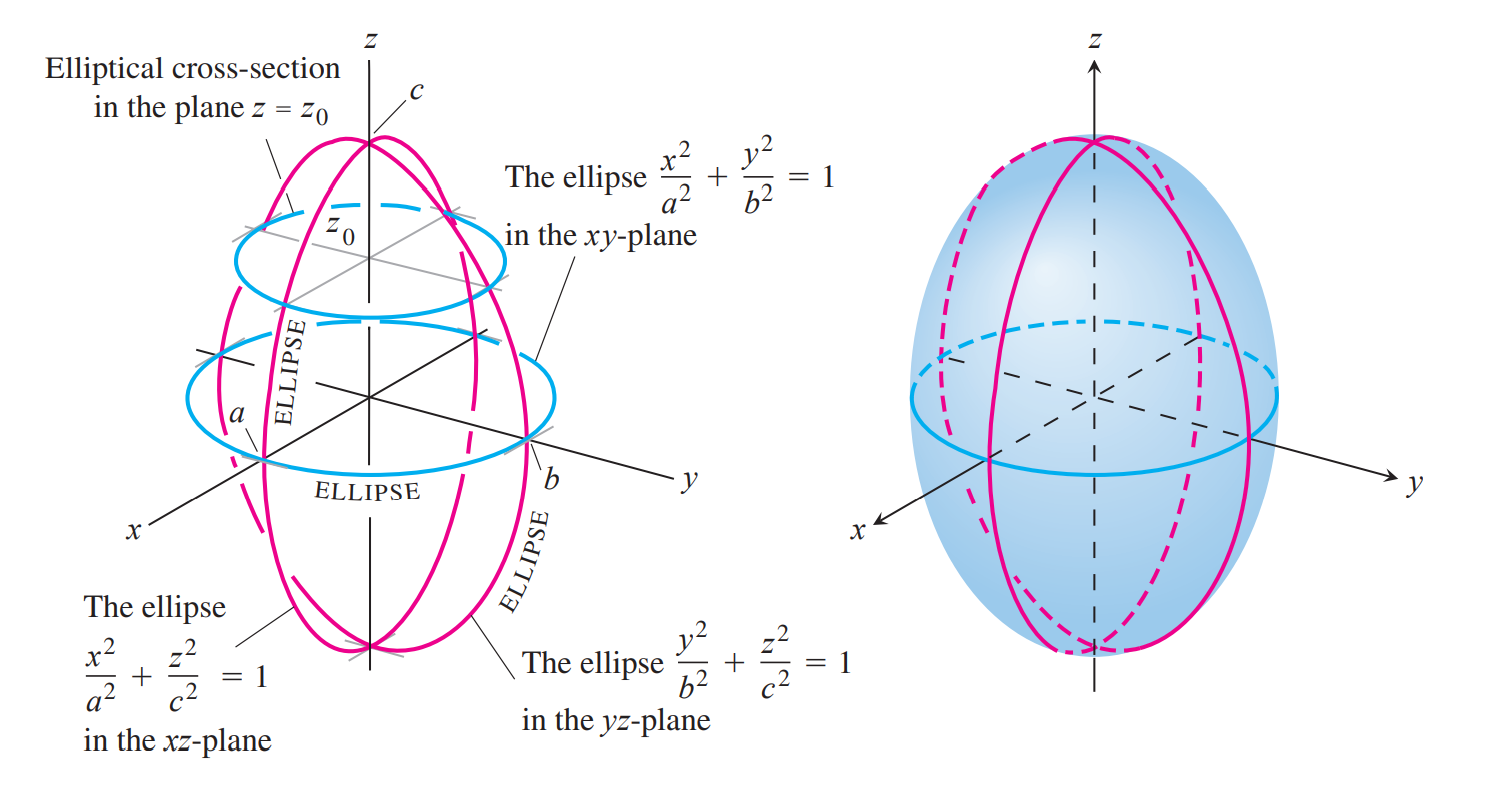
椭球面由椭圆旋转而来

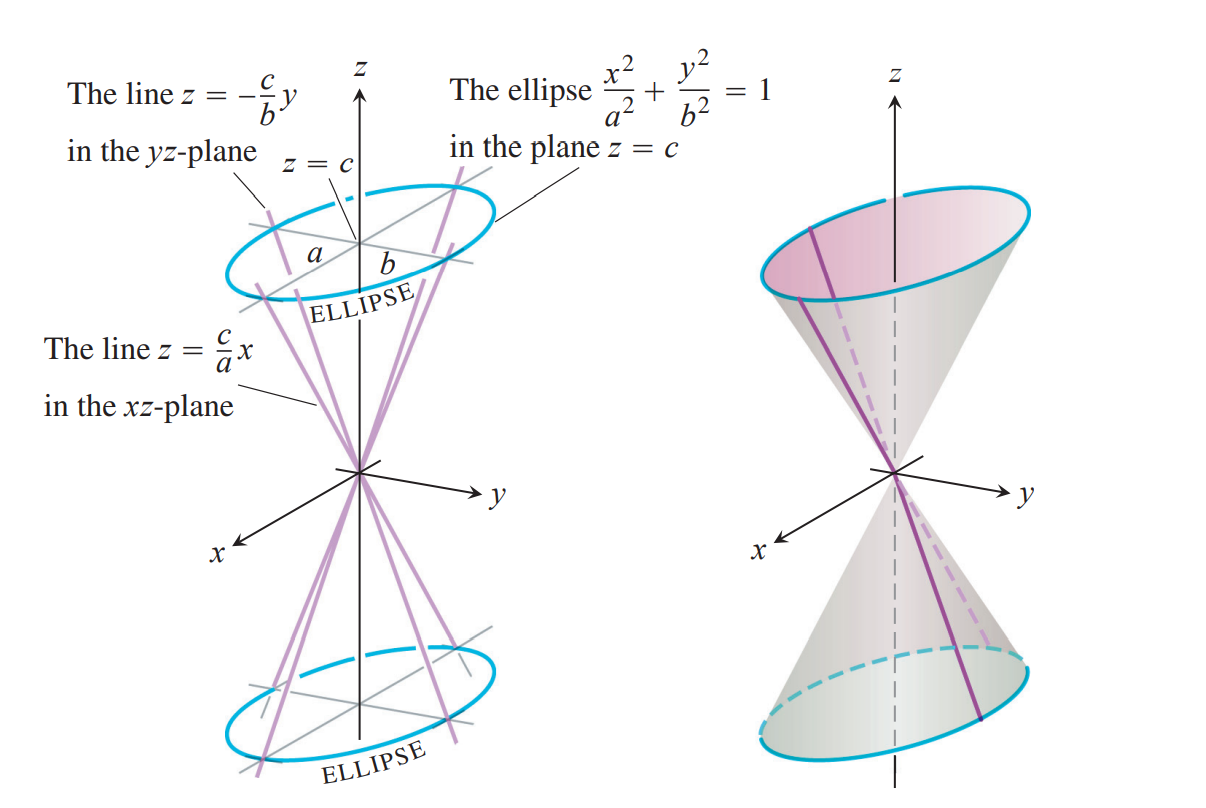
利用截横法有椭圆锥面(两个圆锥)

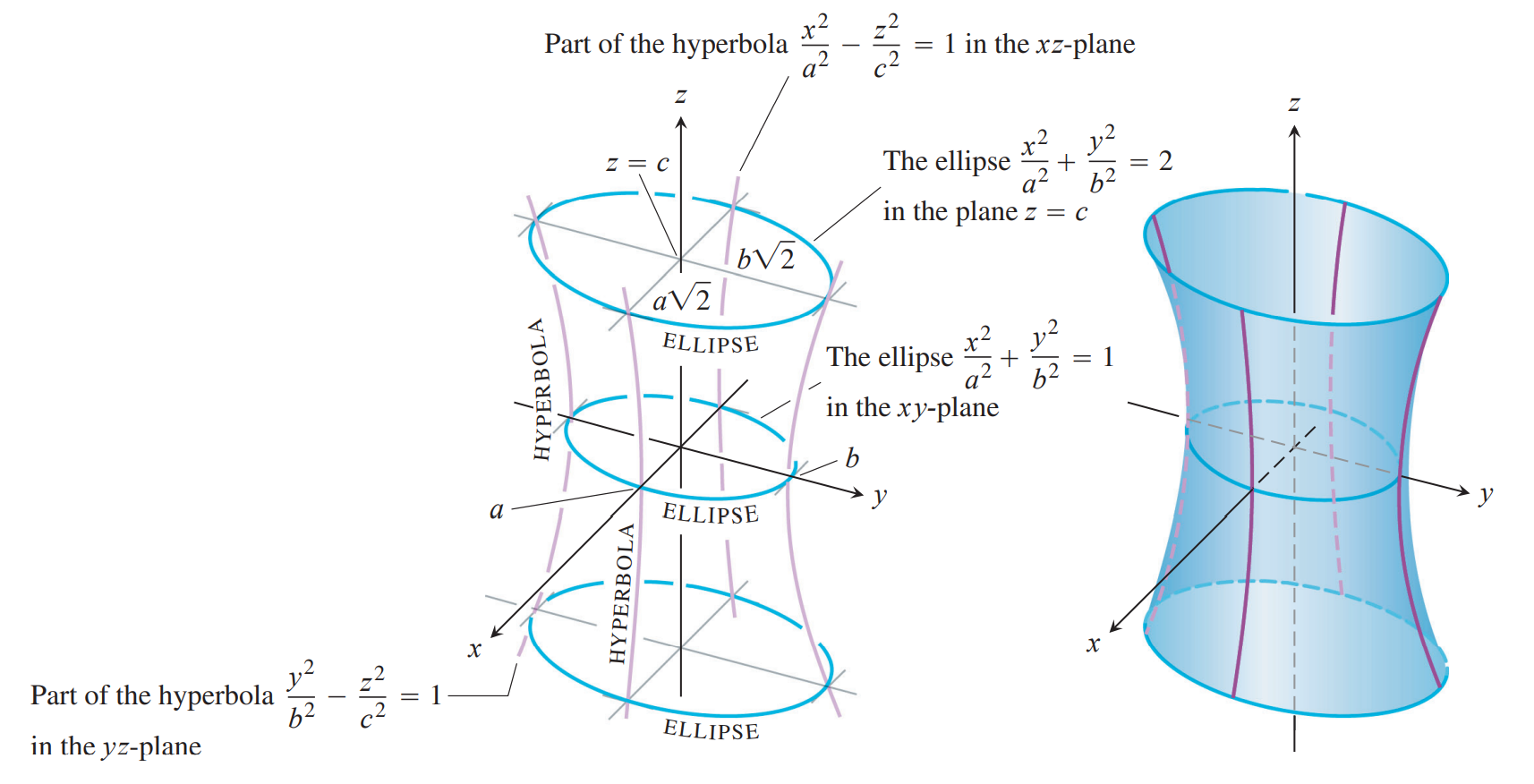
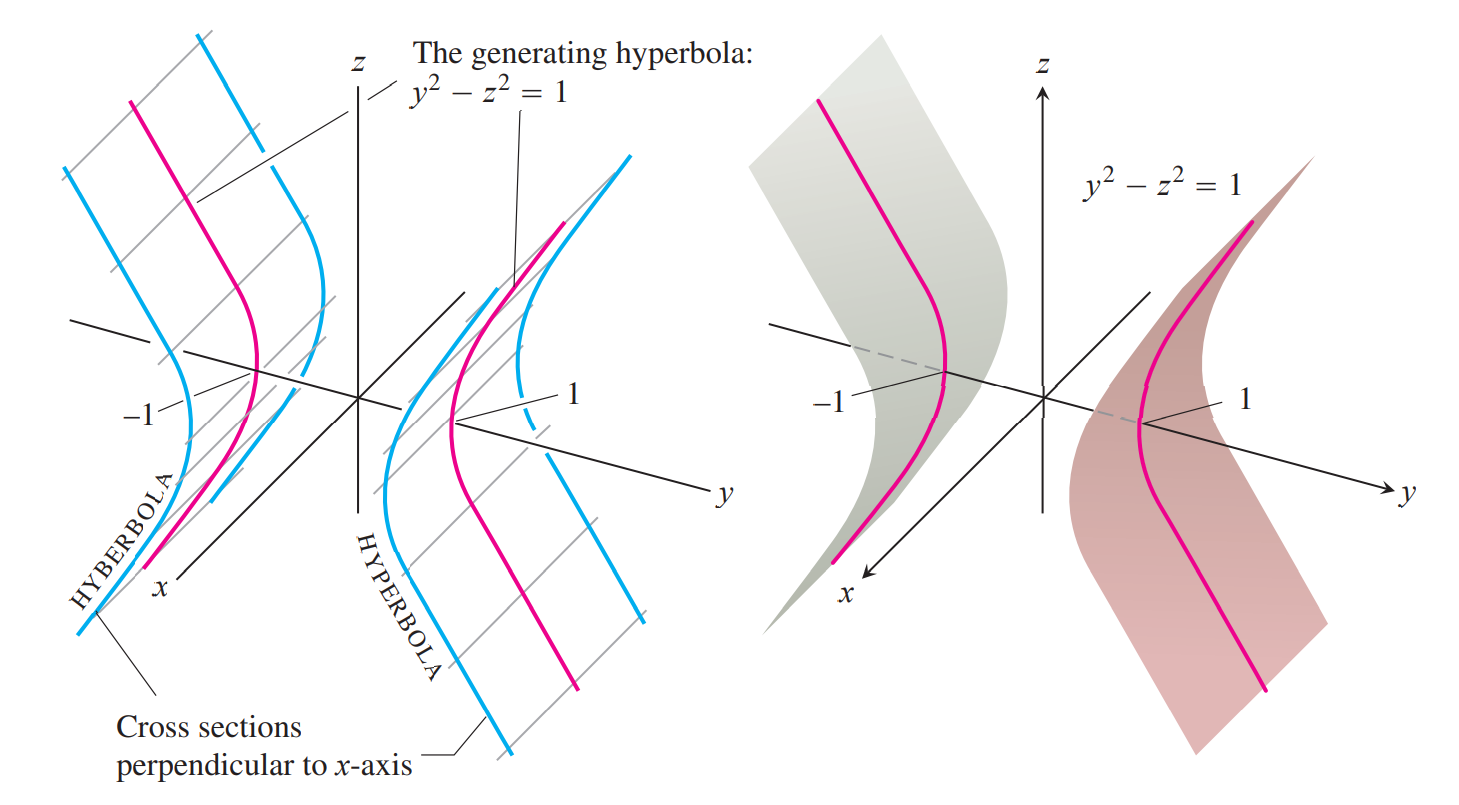
根据旋转轴的不同有单叶和双叶双曲面

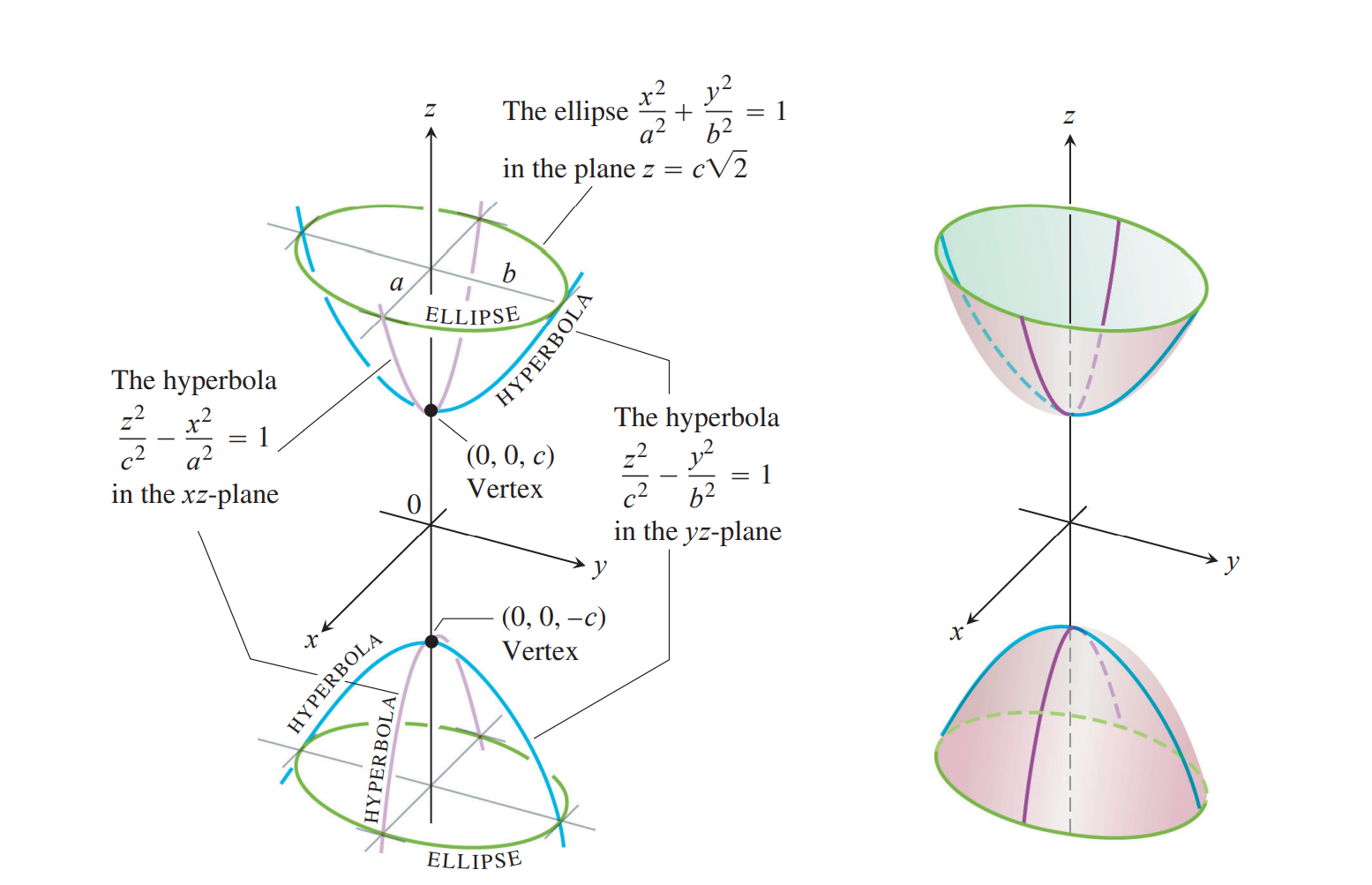
椭圆抛物面是抛物线旋转后伸缩得到的

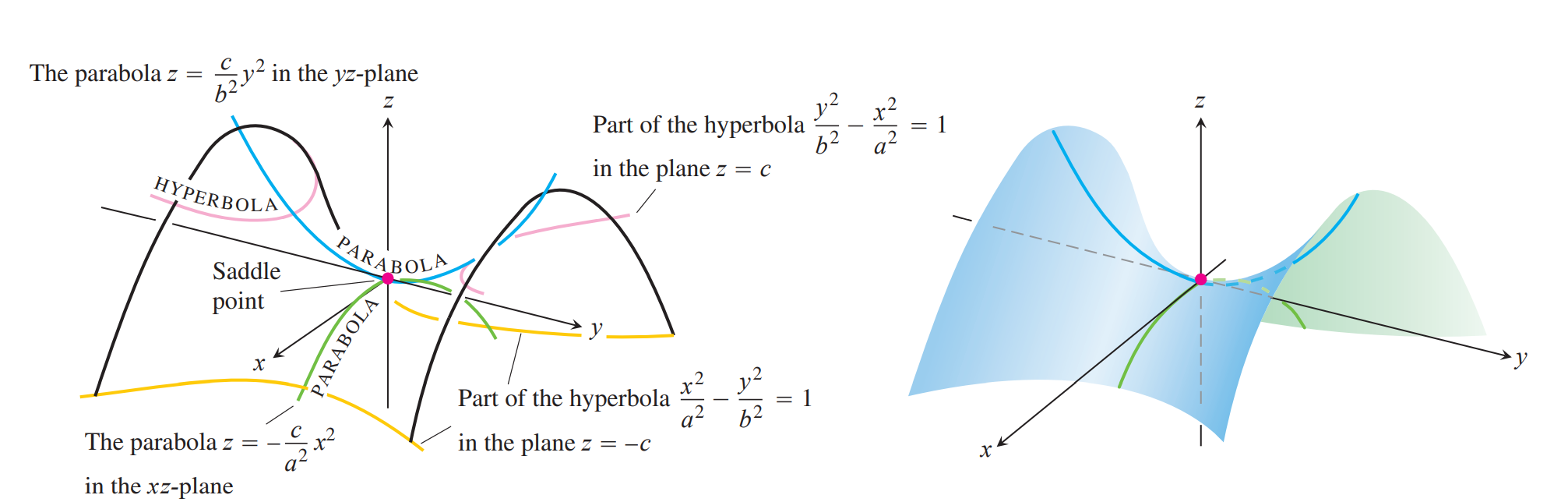
双曲抛物面(马鞍面)

Near the origin, the surface is shaped like a saddle or mountain pass. To a person traveling along the surface in the yz-plane the origin looks like a minimum. To a person traveling in the xz-plane the origin looks like a maximum. Such a point is called a saddle point of a surface

三维曲线

回顾三维直线，消去参数$t$之后可以得到$2$个方程

其实这2个方程表示了2个平面，空间的直线就是这2个平面的交线

从而我们可以引入空间曲线的参数表达式

$$\begin{cases}f(\mathbf p)=0\\g(\mathbf p)=0\end{cases}$$

==点动成线，线动成面，面动成体==

参数方程

由方程表达的曲线和面难以计算

所以我们一般采用参数方程来绘制

对于平面曲线

$$\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}f(t)\\g(t)\end{bmatrix}$$

同理，空间曲线

$$\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}f(t)\\g(t)\\h(t)\end{bmatrix}$$

如螺线(spiral)

$$\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}\cos t\\\sin t\\t\end{bmatrix}$$

三维参数曲面

$$f:\mathbf{R}^2\to \mathbf{R}^3\\ (u,v)\to(x,y,z)$$

如

$$f(u,v)=((2+\cos u)\cos v,(2+\cos u)\sin v,\sin u)$$

球坐标

$$\begin{cases} x = r\sin \theta \cos \phi \\ y = r\sin \theta \sin \phi \\ z = r\cos \theta \end{cases}$$ $$\left\{\begin{aligned} r &= \sqrt {x^2 + y^2 + z^2} \\ \theta &= \operatorname{Arctan} \left(\sqrt{x^2 + y^2}, z \right) \\ \phi &= \operatorname{Arctan} (y, x)\end{aligned}\right.$$

类似经度和纬度

映射

$$f:R^n\to R^m$$

对于$n<m$，为低维到高维的映射，本征维度为$n$

$m<n$，降维映射，一般会损失数据

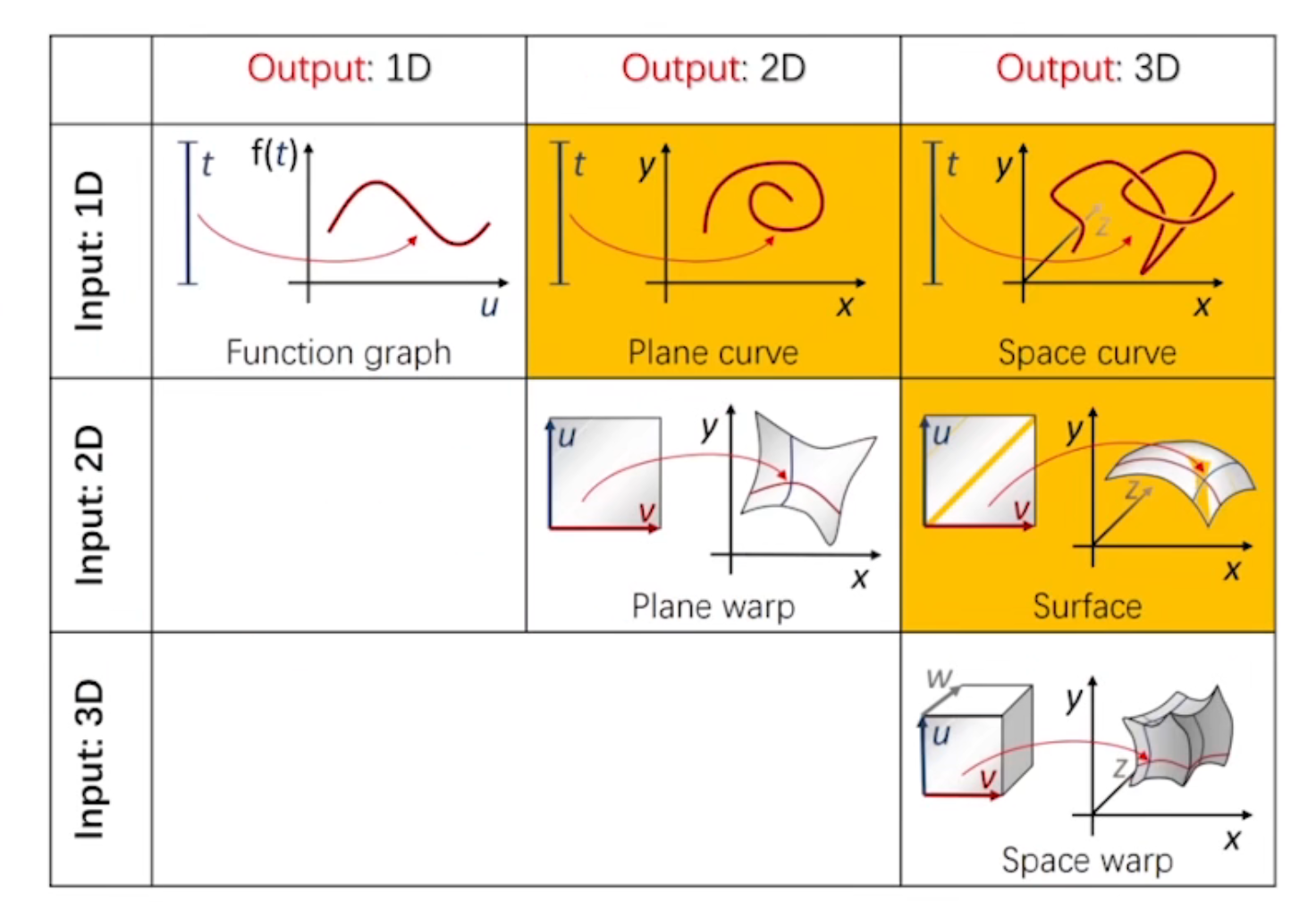
取一小段可以看到仍为本征维度

颜色系统

RGB系统使用三个十六进制数来表示颜色的3个分量红绿蓝

$$\rm \#FFFFFF\to white$$

从$(0,0,0)\to(255,255,255)$

可以得到逐渐变亮的颜色

YCbCr其中Y代表亮度（Luminance或Luma）,也就是灰阶值；而“Cb“和“Cr” 表示的则是色度（Chrominance或Chroma）

$$\rm\begin{cases}Y= 0.257R + 0.504G + 0.098B + 16\\ \rm Cb = -0.148R - 0.291G + 0.439B + 128\\ \rm Cr = 0.439R - 0.368G - 0.071B + 128\end{cases}$$

转为RGB

$$\begin{cases} \rm R= 1.164(Y - 16) + 1.596(Cr - 128)\\ \rm G= 1.164(Y - 16) - 0.813(Cr - 128) - 0.392(Cb - 128)\\ \rm B= 1.164(Y - 16) + 2.017(Cb - 128)\end{cases}$$

白金汉π定理

物理量$q_i$之间满足

$$f(q_1,q_2\dots q_m)=0$$

则有

$$[q_j]=\prod_{i=1}^nX_i^{a_{ij}}\\ A=(a_{ij})_{m\times n}$$

存在$m-\text{Rank} A$个无量纲量$\pi_s$

$\text{Rank} A$为基本物理量的个数

$$F(\pi_1,\pi_2\dots\pi_{m-\text{Rank} A})=0$$

傅里叶变换

$$g(t)-A_0=\sum_{i=0}^\infty A_n\cos(n\omega t+\varphi_n)$$

考虑这个图形的质心

$$g(t)e^{-2\pi ft \text{i}}\\ z_c=\frac1N\sum_{k=0}^{N-1}g(t_k)e^{-2\pi ft_k \text{i}}$$

取极限，并不需平均

$$\hat{g}(f)=\int_{0}^{t_m}g(t)e^{-2\pi ft \text{i}}\text{d}t$$

利用复数的三角形式

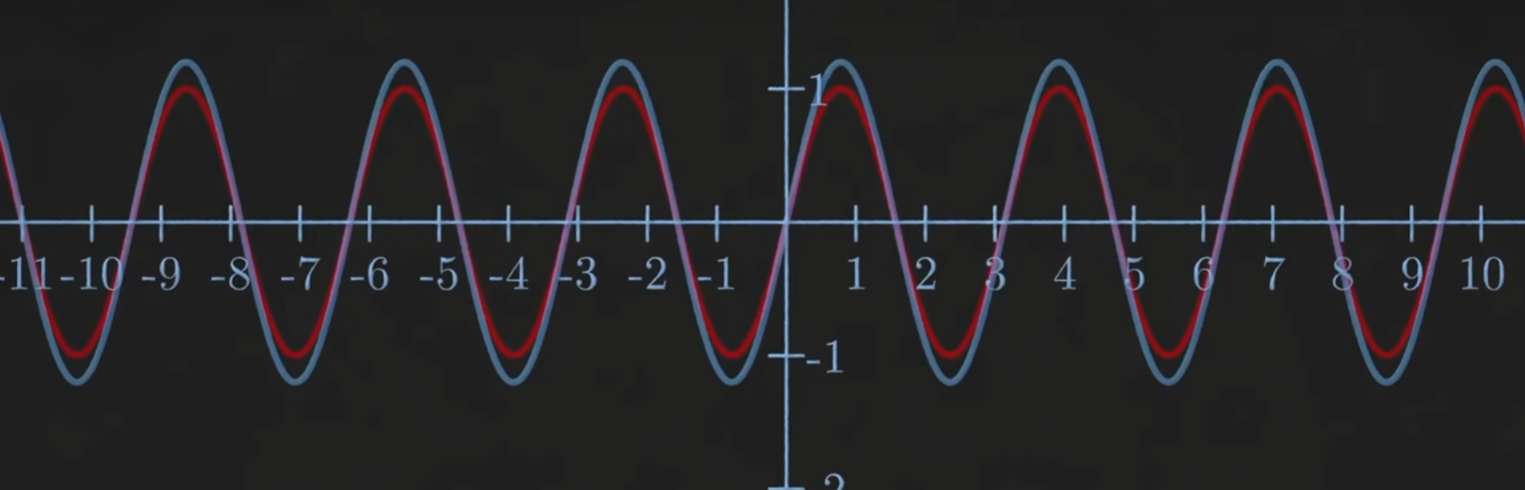
当频率匹配时，积分为正

由三角函数的正交性，若正交，为零

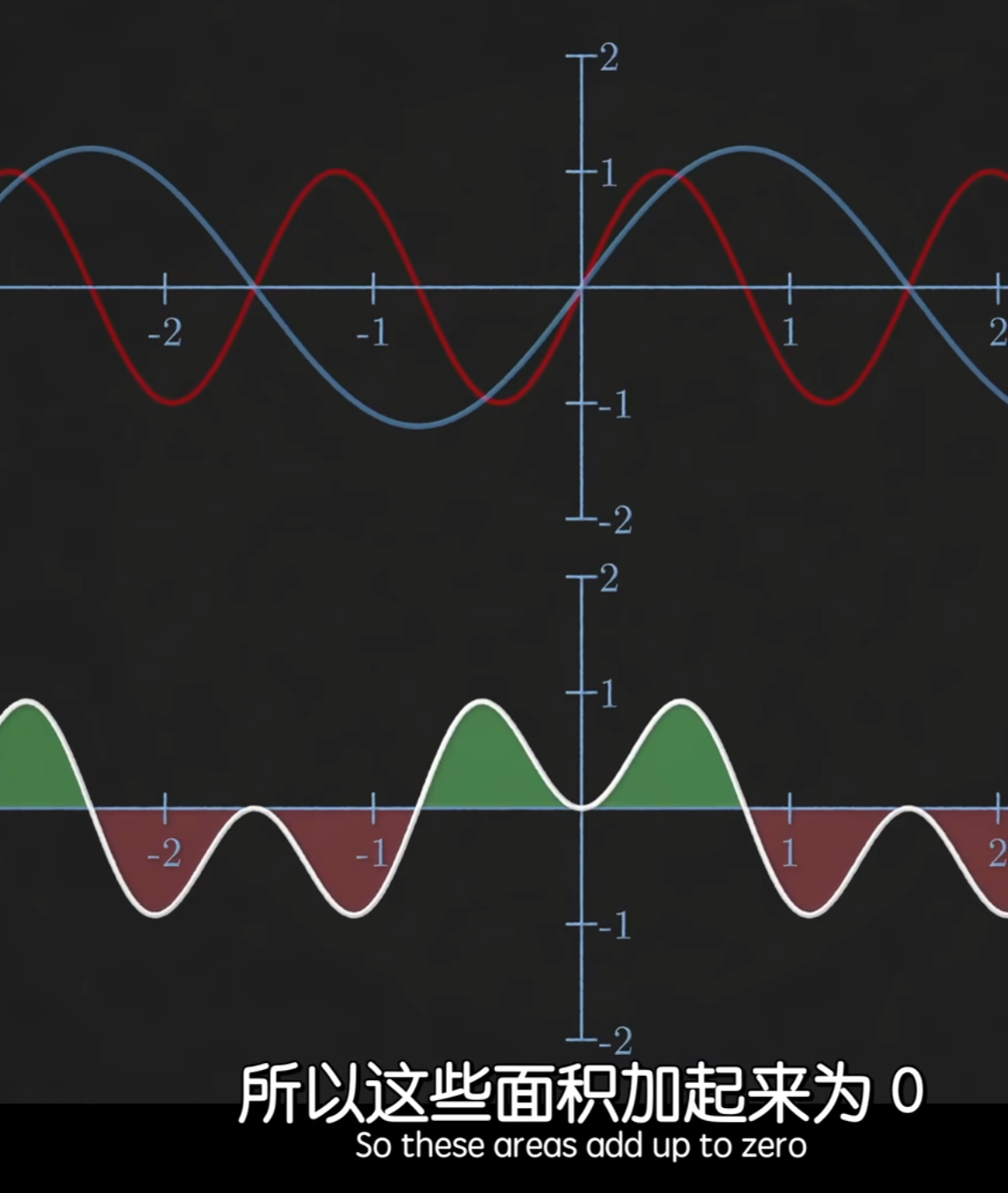
从而得到两个分量$\sin | \cos$的强度

快速傅里叶变换

多项式乘法

对于多项式

$$A(x)=\sum_{i=0}^{n-1}a_ix^{i}\\ B(x)=\sum_{i=0}^{n-1}b_ix^{i}\\ C(x)=A(x)B(x)=\sum_{i=0}^{2n-2}c_ix^{i}\\ c_i=\sum_{j=0}^ia_jb_{i-j}$$

这是多项式的系数表示，但还可以使用点值表示

$$\{(x_0,y_0),(x_1,y_1)\dots(x_{n-1},y_{n-1})\}$$

其中$x_i$各不相同，可以证明两种表示是等价的

$$\left[\begin{array}{c} P\left(x_{0}\right) \\ P\left(x_{1}\right) \\ \vdots \\ P\left(x_{n-1}\right) \end{array}\right]=\left[\begin{array}{ccccc} 1 & x_{0} & x_{0}^{2} & \cdots & x_{0}^{n-1} \\ 1 & x_{1} & x_{1}^{2} & \cdots & x_{1}^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^{2} & \cdots & x_{n-1}^{n-1} \end{array}\right]\left[\begin{array}{c} p_{0} \\ p_{1} \\ \vdots \\ p_{n-1} \end{array}\right]$$

所以$C(x)$可以表达为

$$\{(x_0,y_0y_0'),(x_1,y_1y_1')\dots(x_{2n-2},y_{2n-2}y_{2n-2}')\}$$

利用拉格朗日插值公式

$$A(x)=\sum_{k=0}^{n-1}y_k\frac{\displaystyle\prod_{j\ne k}(x-x_j)}{\displaystyle\prod_{j\ne k}(x_k-x_j)}$$

可以快速将点值表示转化为系数表示

注意到$2n-2$为偶数，使用几何意义去理解

消去引理

$$\omega_{dn}^{dk}=\omega_{n}^{k}\\ \omega_n^{\frac n2}=\omega^\frac12=\omega_2^1=-1$$

折半引理

$$(\omega_n^k)^2=\omega_\frac n2^k\\ (\omega_n^k)^2=(\omega_n^{k+\frac n2})^2\;\;2\theta/2(\theta+\pi)$$

求和引理

对于$\forall n\ge1,n\mod k\ne0$

$$\sum_{j=0}^{n-1}(\omega_n^k)^j=0$$

利用$n$次单位根，带入可以得到

$$y_k=\sum_{j=0}^{n-1}a_j(\omega_n^k)^j$$

从而向量

$$(y_0,y_1,\cdots ,y_{n-1})$$

为系数向量的离散傅里叶变换(DFT)

FFT

$$A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)$$

从而对$k:0\to \frac n 2-1$有

$$\begin{cases}y_k=y^{[0]}_k+\omega_n^ky_k^{[1]}\\ y_{k+n/2}=y^{[0]}_k-\omega_n^ky_k^{[1]}\end{cases}$$

从而分为两个规模为一半的子问题

$$\left[\begin{array}{c} P\left(\omega^{0}\right) \\ P\left(\omega^{1}\right) \\ P\left(\omega^{2}\right) \\ \vdots \\ P\left(\omega^{n-1}\right) \end{array}\right]=\left[\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^{2} & \cdots & \omega^{n-1} \\ 1 & \omega^{2} & \omega^{4} & \cdots & \omega^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{n-1} & \omega^{2(n-1)} & \cdots & \omega^{(n-1)(n-1)} \end{array}\right]\left[\begin{array}{c} p_{0} \\ p_{1} \\ p_{2} \\ \vdots \\ p_{n-1} \end{array}\right]$$ $$\left[\begin{array}{c} p_{0} \\ p_{1} \\ p_{2} \\ \vdots \\ p_{n-1} \end{array}\right]=\frac{1}{n}\left[\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega^{-1} & \omega^{-2} & \cdots & \omega^{-(n-1)} \\ 1 & \omega^{-2} & \omega^{-4} & \cdots & \omega^{-2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{-(n-1)} & \omega^{-2(n-1)} & \cdots & \omega^{-(n-1)(n-1)} \end{array}\right]\left[\begin{array}{c} P\left(\omega^{0}\right) \\ P\left(\omega^{1}\right) \\ P\left(\omega^{2}\right) \\ \vdots \\ P\left(\omega^{n-1}\right) \end{array}\right]$$

而离散傅里叶变换可以写为

$$z_c=\sum_{k=0}^{N-1}g(t_k)e^{-2\pi ft_k \text{i}}$$

这就是带入单位根后的多项式的形式

化简

$$z_c=\sum_{k=0}^{N-1}x_ke^{-2\pi f_rt_k \text{i}}\\$$

总共有N个频率$f_r(0\le r\le n-1)$，让其等距分布

$$\\-2\pi f_rt_k=-2\pi f_r\frac{k}{f_s}$$

等距，所以令

$$\frac{f_r}{rf_s}=\frac1{N}$$

得

$$X_r=\sum_{k=0}^{N-1}x_ke^{-(2\pi/N) rk\text{i}}$$

结果

采样定理告诉我们，采样频率要大于信号频率的两倍

时域到频域，将N个采样点变为N个复数

$$t\to f\\ A\to z$$

设采样频率为$f_s$，则FFT的分辨率为$f_s/N$

$$f_i=\frac{(i-1)f_s}N$$

$z$的模长反映了振幅占比

$$A_i=\frac{2||z_i||}{N}$$

每个分量的相位为对应复数的相位

$$\tan \varphi=\frac{\Im z}{\Re z}$$

由于$Xr$和$X{N-r}$共轭，取模后相等

所以FFT的结果左右是对称的，只需取一般