高中/碰撞

Posted on 2022-07-23

MATLAB模拟碰撞

m=[3,1,2];%小球质量
ball=[5 5;20 10;11 15];%球的坐标
r=[3,4,5];%半径
color=['b','y','r'];%球的颜色
v= rand(3,2)*0.8;%随机生成速度
disp(v)
dt=0.55;
figure
xlim([-5 45])
ylim([-5 35])
while true%逐帧绘制
    yes=[1,1,1];%未处理,防止重复计算
    for i=1:3
        for j=1:3
            if yes(i)
                if i==j
                    if ball(j,1)<r(j) || ball(j,1)>=40-r(j)%x边界
                        v(j,1)=-v(j,1);
                    end
                    if ball(j,2)<r(j) || ball(j,2)>=30-r(j)%y边界
                        v(j,2)=-v(j,2);
                    end
                else
                    distance=sqrt((ball(i,1)-ball(j,1)).^2+(ball(i,2)-ball(j,2)).^2);
                    if distance<=(r(i)+r(j))%速度计算
                        vix=((m(i)-m(j))*v(i,1)+2*m(j)*v(j,1))/(m(i)+m(j));
                        viy=((m(i)-m(j))*v(i,2)+2*m(j)*v(j,2))/(m(i)+m(j));
                        vjx=((m(j)-m(i))*v(j,1)+2*m(i)*v(i,1))/(m(i)+m(j));
                        vjy=((m(j)-m(i))*v(j,2)+2*m(i)*v(i,2))/(m(i)+m(j));
                        v(i,1)=vix;
                        v(i,2)=viy;
                        v(j,1)=vjx;
                        v(j,2)=vjy;
                        yes(j)=0;
                    end    
                end
            end
        end 
    end
    rectangle('Position',[0,0,40,30])
    for i=1:3
        ball(i,:)=ball(i,:)+v(i,:)*dt;%近似匀速
        rectangle('Position',[ball(i,1)-r(i),ball(i,2)-r(i),2*r(i),2*r(i)],'Curvature',[1,1],  'FaceColor',color(i))
    end
    drawnow
    cla%清空
end

高中/笔记

Posted on 2022-07-23

$P\left(\frac{X_{1}+X_{2}+\cdots+X_{n}-n \mu}{\sigma \sqrt{n}} \leq x\right)\to \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} e^{-t^{2} / 2} d t$ $F=G \frac{m_{1} m_{2}}{r^{2}}$ $\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}$ $V-E+F=2$ $\Delta_{\psi}(P) \Delta_{\psi}(X) \geq \hbar$ $H(S) \leq m(S) \leq H(S)+1$ $P \stackrel{?}{=} N P$ $i \hbar \frac{\partial \psi}{\partial t}=\frac{-\hbar^{2}}{2 m} \nabla^{2} \psi+V \psi$ $\frac{1}{\pi}=\frac{\sqrt{8}}{99^{2}} \sum_{n=0}^{\infty} \frac{(4 n) !}{(n !)^{4}} \frac{(1103+26390 n)}{396^{4 n}}$ $l^{\prime}=\frac{l}{\sqrt{1-\frac{v^{2}}{c^{2}} }}$ $\frac{d N}{d t}=r N\left(1-\frac{N}{K}\right)$ $P(A)=(k/N)^n p(B|A)=1-\sum_{i=1}^{k-1}\binom{k}{i}(1-i/k)^n(-1)^{i+1} P\{D=k\}=\binom{N}{k}P(AB)$ $\left\{ \begin{array}{l} U = \frac { Q } { C } = \frac { n q } { C } \\ { a = g - \frac { E q } { m } = g - \frac { U q } { d m } = g - \frac { n q ^ { 2 } } { d m C } } \\ { \frac { d } { 2 } = \frac { 1 } { 2 } a t ^ { 2 } = \frac { 1 } { 2 } ( g - \frac { n q ^ { 2 } } { d m C } ) \cdot ( \frac { L } { v _ { 0 } } ) ^ { 2 } } \end{array} \right .\Rightarrow n = ( g - \frac { d v _ { 0 } ^ { 2 } } { L ^ { 2 } } ) \cdot \frac { d m C } { q ^ { 2 } }$ $\oint IR=0$ $\left \{\begin{array}{l}x=x_0+t\cos\theta,\\y=y_0+t\sin\theta \end{array}\right .(\theta\in [0,\pi])$ $\rho =\frac{ep}{1-e\cos\theta}$ $\frac {x^2} {a^2}\pm \frac {y^2} {b^2}=1$ $\left\{ \begin{array}{l}m\frac{v^2}{r}=Bqv\\T=\frac {2\pi r} v \end{array}\right .\Rightarrow T=\frac{2\pi m} {Bq}\Rightarrow t=\frac{\theta m} {Bq}$ $\sum_{i = 1}^{k} i ^ {2} = \frac{k {(k + 1)} {(2 k + 1)}}{6}\\$ $\begin{array} {}\sum_\limits{i = 1}^{k+1}i^{2}&= \sum_\limits{i = 1}^{k} i ^ {2}+(k+1)^2\\&= \frac{k {(k + 1)} {(2 k + 1)+6(k+1)^2}}{6}\\&=\frac{(k + 1)(2k^2+7k+6)}{6}\\&=\frac{(k + 1)[(k+1)+1][2(k+1)+1]}{6}\end{array}$ $t=(1+x)^n-1\rightarrow0\\ \begin{array} {aligned}\lim_\limits{x \to 0} \frac{(1+x)^n-1}{x}(n\in R)&=\lim_\limits{x \to 0}[\frac{(1+x)^n-1}{\ln(1+x)^n}\cdot\frac{n\ln(1+x)}{x}]\\&=\lim_\limits{x \to 0} \frac{t}{\ln(1+t)}\cdot\lim_\limits{x \to 0}\frac{n\ln(1+x)}{x}\\&=\frac 1 e\cdot e\cdot n\\&=n\end{array}\\ (1+x)^\alpha\thicksim 1+\alpha x(x\rightarrow0)$ $(1+x)^n> 1+n x\;(n>1,n\in N^*)\\ ( 1 + x ) ^ { k } > 1 + k x\\ \begin{array} {aligned} ( 1 + x ) ^ { k + 1 } &= ( 1 + x ) ( 1 + x ) ^ { k } \\&>{ ( 1 + x ) ( 1 + k x ) }\\ &={ 1 + x + k x + k x ^ { 2 } }\\ &> {1 + ( k + 1 ) x }\end{array}$ $\int^{t}_{0}\mathrm{d}t =-\int_{v_0}^{v}\frac{mR}{B^2L^2v}\mathrm{d}v$ $\int \textrm{efforts}+\texttt{immaturity}+\textrm{d}\textbf{lucky}=Success$ $\frac{d}{dx}(f(x)+g(x))=\frac {df}{dx}+\frac{dg}{dx}$ $\int_{a}^{b}f(x)dx=F(b)-F(a)$ $-2^{w-1}\le x<2^{w-1}-1\qquad \textrm{and}\qquad-2^{w-1}\le y<2^{w-1}-1\qquad\\ x+y=\left\{\begin{array}{l}x+y-2^w,\quad x+y\ge 2^{w-1}\\x+y,\quad 2^{w-1}\le x+y<2^{w-1}\\x+y-2^w,\quad x+y<-2^{w-1}\end{array}\right.$ $\textrm{binary to unsigned}\\ B2U_w(\overrightarrow{x})=x_{w-1}\cdot 2^{w-1}+x_{w-2}\cdot 2^{w-2}+\cdot\cdot\cdot+x_0\cdot2^0=\sum_{i=0}^{w-1}x_i\cdot 2^i$ $\textrm{binary to two's complement representation}\\ B2U_w(\overrightarrow{x})=x_{w-1}\cdot -2^{w-1}+x_{w-2}\cdot 2^{w-2}+\cdot\cdot\cdot+x_0\cdot2^0=x_{w-1}\cdot -2^{w-1}+\sum_{i=0}^{w-2}x_i\cdot 2^i$ $x\cdot2^k=x<<k$ $x=d_md_{m-1}…d_1d_0.d_{-1}…d_{-(n-1)}d_{-n}\\ x=\sum_{i=-n}^{m}d_i\cdot10^i$ $float=>V=(-1)^s\times M\times2^E\\ E=e-bias(bias=2^{8-1}-1=127) \\e\in[1,255]\\E\in[-126,127]\\M=1+f=1.f_{22}f_{21…}f_1$ $\bar{F} =\frac{m_0}{l_1}\sum_{i=1}^{N}v_{ix}^2$ $p=n_0kTe^{-\frac{m_0gh}{kT}}$ $\rm Youth\;passes,but\;with\;luck\;immaturity\;can\;last\;a\;lifetime.$

高中/等边三角形

Posted on 2022-07-23

1.在正方形中折出等边三角形

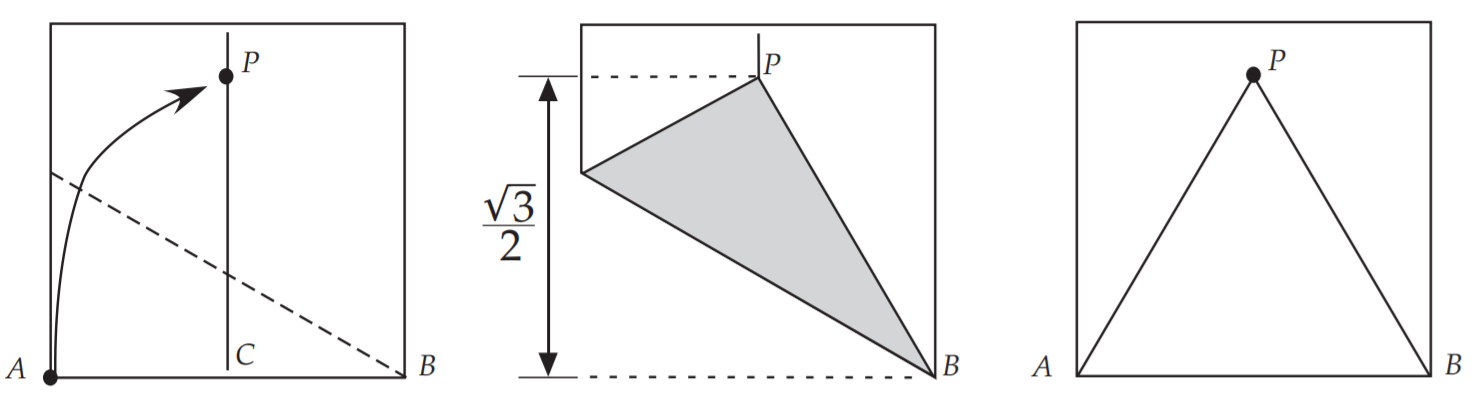
要折等边三角形，首先要折出$60{\circ}$的角，以下是最容易的一种方法

如何让三角形最大呢

如果等边三角形的三个顶点没有落在正方形的四条边上，那么可以放大三角形让它落在边上
如果有顶点落在边上，可以平移，旋转该三角形，使其某一顶点落在正方形的任意顶点上

所以我们只需要研究某一个顶点和正方形的顶点重合的等边三角形

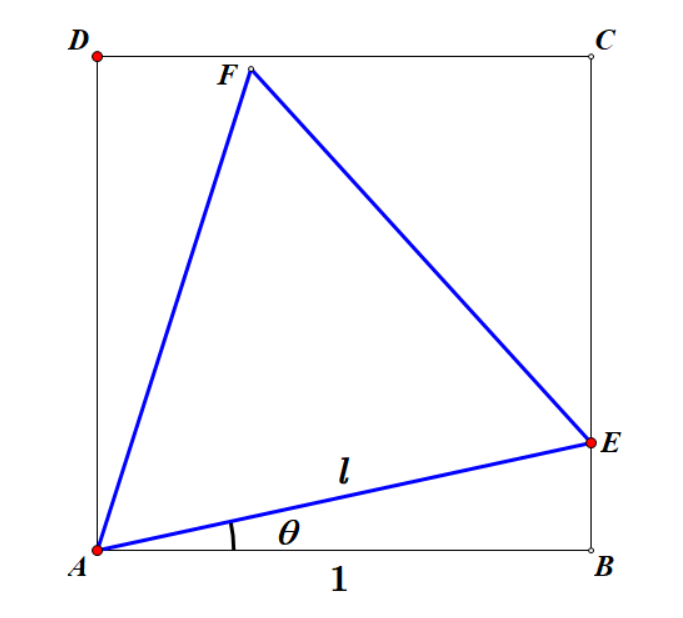
画出图形，由几何关系，三角形的边长$l$可以用$\theta$表达
$
l=1 / \cos \theta=\sec \theta
$
故面积$S$为
$
S(\theta)=\frac{\sqrt{3}}{4} \sec ^{2} \theta
$
根据对称性，我们只需要考虑$0^{\circ} \leq \theta \leq 15^{\circ}$的情况

因为$\cos \theta $在$0^{\circ} \leq \theta \leq 15^{\circ}$单调递减

所以$\sec\theta=\frac{1}{ {\cos \theta } }$在$0^{\circ} \leq \theta \leq 15^{\circ}$单调递增

或对面积求导
$
\frac{\mathrm{d}S}{\mathrm{d} \theta } =2\cdot \frac{\sqrt{3}}{4} \cdot \frac{1}{\cos\theta } \cdot -\frac{1}{\cos ^{2} \theta}\cdot
-\sin \theta =\frac{\sqrt[]{3}\sin \theta }{2\cos^{3} \theta }
$
当$\theta=15^{\circ}$时有最大值

故此时$l=\sqrt{6}-\sqrt{2}=1.035$

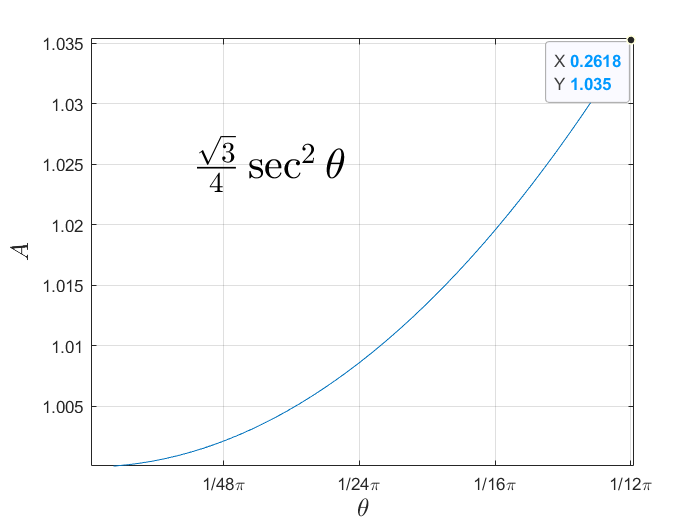
untitled

或者用几何方法分析
$\begin{array}{l}l &=\sqrt{AB^2+BE^2} \&=\sqrt{1+BE^2}\end{array}$
当$BE$最大时边长有最大值

$\therefore\begin{array}{l}S &=\frac12l^2\sin60^\circ \&=\frac{\sqrt{3}}{4}\times(\frac{AB}{\cos15^\circ})^2\end{array}\$

由半角公式得

$\begin{array}{l}\sin15^\circ &=\sqrt{\frac{1-\sin30^\circ}{2}}\&=\frac12\sqrt{2-\sqrt3} \&=\frac12\sqrt{(\frac{\sqrt6}{2})^2-2\cdot\frac{\sqrt6}{2}\cdot\frac{\sqrt2}{2}+(\frac{\sqrt2}{2})^2} \&=\frac12\sqrt{(\frac{\sqrt6}{2}-\frac{\sqrt2}{2})^2} \&=\frac{\sqrt6-\sqrt2}{4}\end{array}$

$\begin{array}{l}\cos15^\circ &=\sqrt{\frac{1+\cos30^\circ}{2}} \&=\frac{\sqrt6+\sqrt2}{4}\end{array}$

或使用两角和与差公式$\sin(\theta\pm\phi)=\sin\theta\cos\phi\pm\cos\theta\sin\phi$有

$\begin{array}{l}\sin15^\circ &=\sin(60^\circ-45^\circ)\&=\sin60^\circ\cos45^\circ-\cos60^\circ\sin45^\circ\&=\frac{\sqrt6-\sqrt2}{4}\end{array}$

$\begin{array}{l}\cos15^\circ &=\sqrt{1-\sin15^\circ} \&=\frac{\sqrt6+\sqrt2}{4}\end{array}$

故$S=\frac{\sqrt{3}}{4}(\frac{4}{\sqrt6+\sqrt2})^2=2\sqrt3-3$

triangle

高中/考纲

Posted on 2022-07-23

数学

能力要求

能力是指空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力
以及应用意识和创新意识.
1.空间想象能力:能根据条件作出正确的图形根据图形想象出直观形象;能正确地分析
出图形中的基本元素及其相互关系;能对图形进行分解、组合;会运用图形与图表等手段形
象地揭示问题的本质.
空间想象能力是对空间形式的观察、分析、抽象的能力,主要表现为识图、画图和对图
形的想象能力.识图是指观察研究所给图形中几何元素之间的相互关系;画图是指将文字语
言和符号语言转化为图形语言以及对图形添加辅助图形或对图形进行各种变换;对图形的想
象主要包括有图想图和无图想图两种,是空间想象能力高层次的标志.
2.抽象概括能力:抽象是指舍弃事物非本质的属性揭示其本质的属性;概括是指把仅仅
属于某一类对象的共同属性区分出来的思维过程.抽象和概括是相互联系的，没有抽象就不可

能有概括，而概括必须在抽象的基础上得出某种观点或某个结论.
抽象概括能力是对具体的、生动的实例,经过分析提炼,发现研究对象的本质;从给定的
大量信息材料中概括出—些结论，并能将其应用于解决问题或做出新的判断.
3.推理论证能力:推理是思维的基本形式之一，它由前提和结论两部分组成;论证是由已
有的正确的前提到被论证的结论的一连串的推理过程.推理既包括演绎推理,也包括合情推理;
论证方法既包括按形式划分的演绎法和归纳法，也包括按思考方法划分的直接证法和间接证
法.一般运用合情推理进行猜想，再运用演绎推理进行证明.
中学数学的推理论证能力是根据已知的事实和已获得的正确数学命题,论证某一数学命
题真实性的初步的推理能力.
4.运算求解能力:会根据法则、公式进行正确运算、变形和数据处理,能根据问题的条件
寻找与设计合理、简捷的运算途径，能根据要求~~对数据进行估计和近似计算~~.
运算求解能力是思维能力和运算技能的结合.运算包括对数字的计算、估值和近似计算,
对式子的组合变形与分解变形，对几何图形各几何量的计算求解等.运算能力包括分析运算条
件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力,也包括在实
施运算过程中遇到障碍而调整运算的能力.
5.数据处理能力:会收集、整理、分析数据,能从大量数据中抽取对研究问题有用的信息，
并做出判断.
数据处理能力主要是指针对研究对象的特殊性，选择合理的收集数据的方法，根据问题
的具体情况，选择合适的统计方法整理数据，并构建模型对数据进行分析、推断，获得结论.

6.应用意识:能综合应用所学数学知识、思想和方法解决问题，包括解决相关学科、生产、
生活中简单的数学问题;能理解对问题陈述的材料，并对所提供的信息资料进行归纳、整理
和分类,将实际问题抽象为数学问题;能应用相关的数学方法解决问题进而加以验证，并能用
数学语言正确地表达和说明.应用的主要过程是依据现实的生活背景提炼相关的数量关系，
将现实问题转化为数学问题，构造数学模型,并加以解决.
7.创新意识:能发现问题、提出问题,综合与灵活地应用所学的数学知识、思想方法，选
择有效的方法和手段分析信息，进行独立的思考、探索和研究,提出解决问题的思路，创造性地
解决问题.
创新意识是理性思维的高层次表现.对数学问题的“观察、猜测、抽象、概括、证明”，是
发现问题和解决问题的重要途径，对数学知识的迁移、组合、融会的程度越高,显示出的创新
意识也就越强.

个性品质要求.
个性品质是指考生个体的情感、态度和价值观.要求考生具有一定的数学视野，认识数学
的科学价值和人文价值，崇尚数学的理性精神,形成审慎的思维习惯,体会数学的美学意义.
要求考生克服紧张情绪，以平和的心态参加考试,合理支配考试时间，以实事求是的科学
态度解答试题,树立战胜困难的信心,体现锲而不舍的精神.

考查要求
数学学科的系统性和严密性决定了数学知识之间深刻的内在联系,包括各部分知识的纵
向联系和横向联系，要善于从本质上抓住这些联系，进而通过分类、梳理、综合,构建数学试卷
的框架结构.
1.对数学基础知识的考查,既要全面又要突出重点对于支撑学科知识体系的重点内容，要
占有较大的比例,构成数学试卷的主体.注重学科的内在联系和知识的综合性,不刻意追求知
识的覆盖面.从学科的整体高度和思维价值的高度考虑问题,在知识网络的交汇点处设计试题，
使对数学基础知识的考查达到必要的深度.
2.对数学思想方法的考查是对数学知识在更高层次上的抽象和概括的考查，考查时必须
要与数学知识相结合，通过对数学知识的考查，反映考生对数学思想方法的掌握程度.
3.对数学能力的考查,强调“以能力立意”,就是以数学知识为载体，从问题入手，把握学科
的整体意义，用统一的数学观点组织材料,侧重体现对知识的理解和应用，尤其是综合和灵活
的应用，以此来检测考生将知识迁移到不同情境中去的能力,从而检测出考生个体理性思维的
广度和深度以及进- 步学习的潜能.
对能力的考查要全面,强调综合性、应用性，并要切合考生实际对推理论证能力和抽象概
括能力的考查贯穿于全卷,是考查的重点,强调其科学性、严谨性、抽象性;对空间想象能力
的考查主要体现在对文字语言、符号语言及图形语言的互相转化上;对运算求解能力的考查
主要是对算法和推理的考查,考查以代数运算为主;对数据处理能力的考查主要是考查运用
概率统计的基本方法和思想解决实际问题的能力.
4.对应用意识的考查主要采用解决应用问题的形式.命题时要坚持“贴近生活，背景公平，
控制难度”的原则,试题设计要切合中学数学教学的实际和考生的年龄特点，并结合实践经验,
使数学应用问题的难度符合考生的水平.
5.对创新意识的考查是对高层次理性思维的考查.在考试中创设新颖的问题情境,构造有
一定深度和厂度的数学问题时，要注重问题的多样化，体现思维的发散性;精心设计考查数学
主体内容、体现数学素质的试题;也要有反映数、形运动变化的试题以及研究型、探索型、
开放型等类型的试题.
数学科的命题,在考查基础知识的基础上，注重对数学思想方法的考查,注重对数学能力
的考查,展现数学的科学价值和人文价值，同时兼顾试题的基础性、综合性和应用性，重视试题
间的层次性,合理调控综合程度,坚持多角度、多层次的考查,努力实现全面考查综合数学素
养的要求,促进学生德智体美劳全面发展.

语文

化学

1.接受、吸收、整合化学信息的能力
(1)对中学化学基础知识能正确复述、再现、辨认，并能融会贯通。
(2)通过对自然界、生产和生活中的化学现象的观察，以及实验现象、实物、模型的
观察，对图形、图表的阅读，获取有关的感性知识和印象，并进行初步加工、吸收、有序存
储。
(3)从提供的新信息中，准确地提取实质性内容，并与已有知识整合，重组为新知识
块。
2.分析和解决化学问题的能力
(1)将实际问题分解，通过运用相关知识，采用分析、综合的方法，解决简单化学问
题。
(2)将分析和解决问题的过程及成果，能正确地运用化学术语及文字、图表、模型、
图形等进行表达，并做出合理解释。
3.化学实验与探究的能力
(1)掌握化学实验的基本方法和技能，并初步实践化学实验的- -般过程。
(2)在解决化学问题的过程中，运用化学原理和科学方法，能设计合理方案，初步实
践科学探究。

生物

1.理解能力
(1)能理解所学知识的要点，把握知识间的内在联系，形成知识的网络结构。
(2)能用文字、图表以及数学方式等多种表达形式准确地描述生物学方面的内容。
(3)能运用所学知识与观点，通过比较、分析与综合等方法对某些生物学问题进行解
释、推理，做出合理的判断或得出正确的结论。
2.实验与探究能力
(1)能独立完成“生物知识内容表”所列的生物实验，包括理解实验目的、原理、方
法和操作步骤，掌握相关的操作技能，并能将这些实验涉及的方法和技能等进行运用。
(2)具备验证简单生物学事实的能力，能对实验现象和结果进行分析、解释，并能对
收集到的数据进行处理。
(3)具有对一些生物学问题进行初步探究的能力，包括运用观察、实验与调查、假说
演绎、建立模型与系统分析等科学研究方法。
(4)能对一些简单的实验方案做出恰当的评价和修订。
3.获取信息的能力
(1)能从提供的材料中获取相关的生物学信息，并能运用这些信息，结合所学知识解
决相关的生物学问题。
(2)关注对科学、技术和社会发展有重大影响的、与生命科学相关的突出成就及热点问
题。

4.综合运用能力
理论联系实际，综合运用所学知识解决自然界和社会生活中的一些生物学问题。

高中/芳贺定理

Posted on 2022-07-23

1.芳贺第一定理

日本筑波大学生物学教授芳贺和夫（Kazuo Haga），在等待实验结果的时候喜欢用摺纸打发时间。他发现了以下的有趣结果。

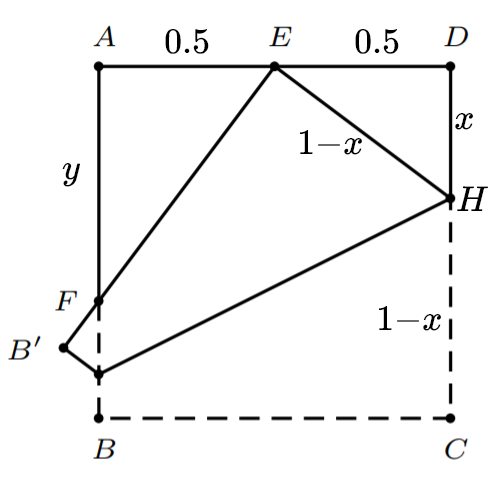
$Claim:F$为$AB$的三等分点

$proof:$

设正方形边长为1，将$C$折到$AD$的中点$E$处，由图

$x^{2}+\left(\frac{1}{2}\right)^{2}=(1-x)^{2}$

解得$x=\frac{3}{8}$

又$\triangle FAR \sim \triangle EDH$

$\frac{y}{\frac{1}{2}}=\frac{\frac{1}{2}}{x}$

解得$y=\frac{2}{3}$

$Property:$

推广：

$x^{2}+k^{2}=(1-x)^{2}$ $\frac{y}{1-k}=\frac{k}{x}$

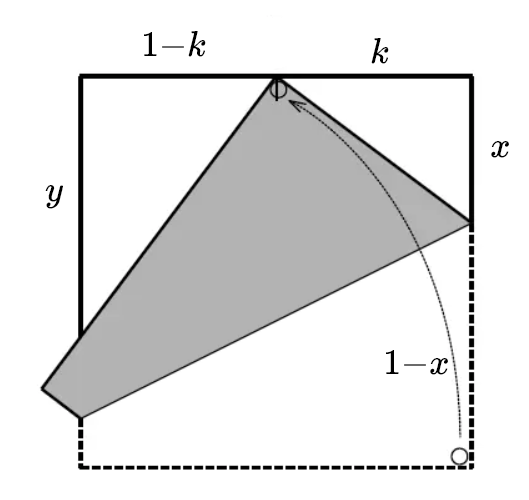
通过相似三角形和勾股定理，联立两个方程

$\frac{y}{1-k}=\frac{k}{\left(1-k^{2}\right) / 2}$ $\frac{y}{2}=\frac{k}{1+k}$

若正方形边长为1，有$k=\frac{1}{N}$，带入得到

$\frac{y}{2}=\frac{1 / N}{1+1 / N}=\frac{1}{N+1}$

如果一直按此方法重复，就可以由$n$等分得到$n+1$等分，于是便得到了任意等分 ~~有点麻烦~~

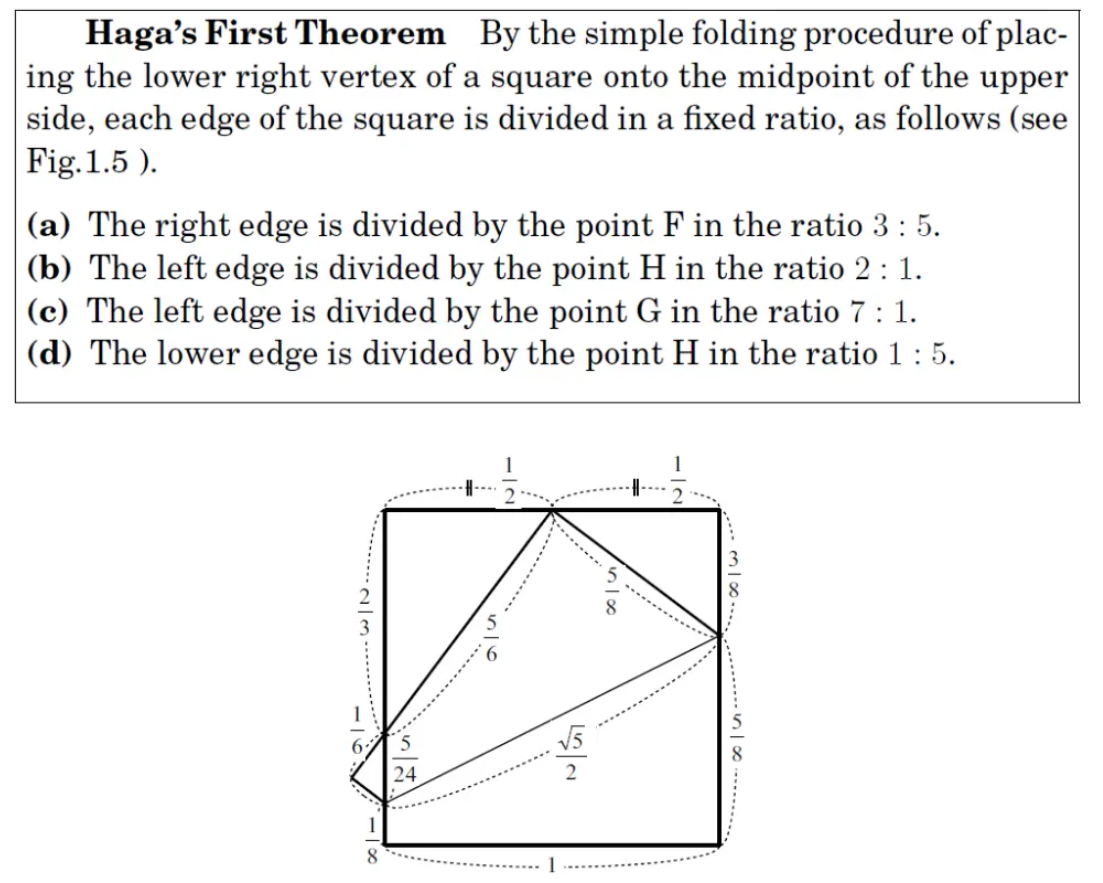注意左上角的直角三角形，它是一个$3:4:5$的直角三角形，难道这只是巧合吗

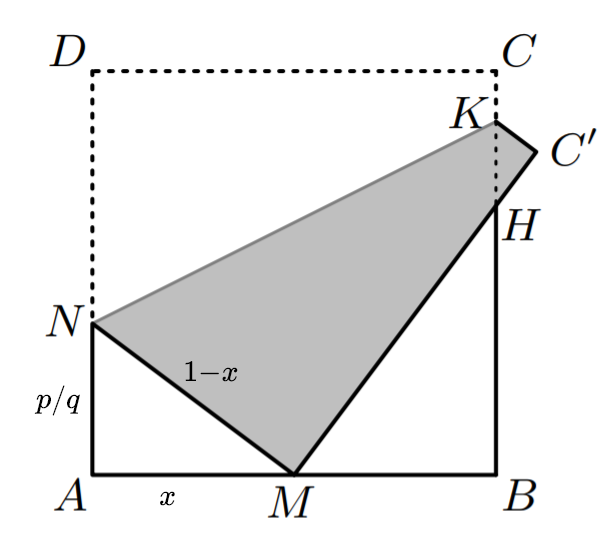
$A B=1, A N=x $及$A M=\frac{p}{q} $其中 $p, q \in \mathbb{N}, M N=1-x $

$\begin{aligned} \left(\frac{p}{q}\right)^{2}+x^{2} &=(1-x)^{2} \\ \frac{p^{2}}{q^{2}}+x^{2} &=1-2 x+x^{2} \\ x &=\frac{q^{2}-p^{2}}{2 q^{2}} \end{aligned}$

所以，

$\begin{aligned} A N: A M: M N &=\frac{q^{2}-p^{2}}{2 q^{2}}: \frac{p}{q}: 1-\frac{q^{2}-p^{2}}{2 q^{2}} \\ &=q^{2}-p^{2}: 2 p q: p^{2}+q^{2} \end{aligned}$

所以只要$p$和$q$是整数，那么这三条边的比就一定是勾股数

$\begin{array}{|l|l|} \hline p / q & A N: A M: M N \\ \hline 1 / 2 & 3: 4: 5 \\ \hline 2 / 3 & 5: 12: 13 \\ \hline 1 / 4 & 15: 8: 17 \\ \hline \end{array}$

2.芳贺第二定理

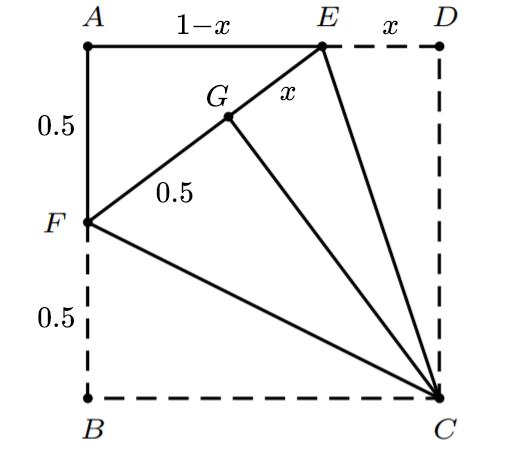
将$AB$沿$CF$折叠，延长$FG$交$AD$于$E$

在$\triangle AEF$中，有

$(1-x)^{2}+(\frac{1}{2})^{2}=(x+\frac{1}{2})^2$

解得$x=\frac{1}{3}$，即$E$是$AD$的三等分点

3.芳贺第三定理

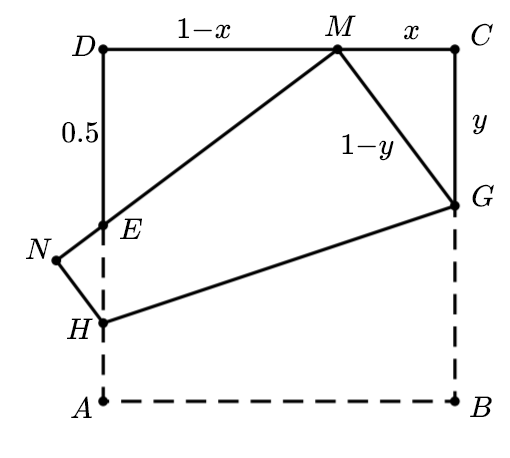
设正方形 $ABCD$的边长为1,$ C M$=$x$, $C G$=$y$

将$AB$边折到$AD$中点$E$上，并让$B$点落在$CD$上

由 $\triangle E D M \sim \triangle C M G$, 可得

$\frac{D E}{D M}=\frac{C M}{C G}$

在$\triangle C M G$ 中, $G M $=$ 1-CG=1-y$，有

$x^{2}+y^{2}=(1-y)^{2}$

解之得

$y=\frac{1-x^{2}}{2}$

带入得$x=\frac{1}{3}$，即点$M$是$ C D $的三等分点.

4.再谈n等分

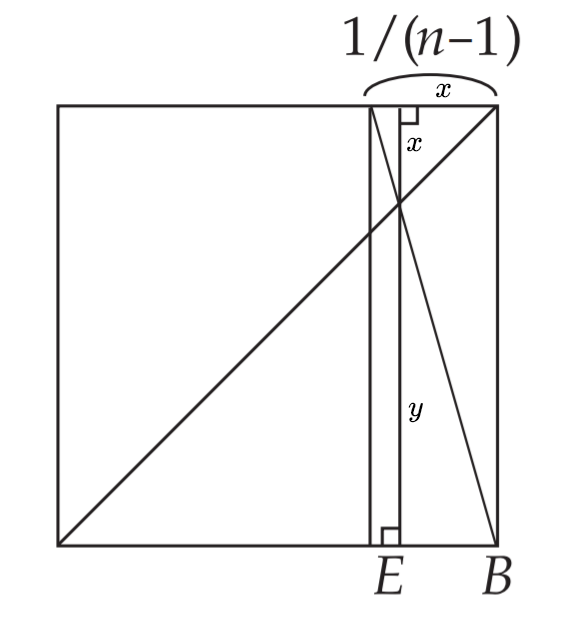
如果我们得到了$n-1$等分，在图中不难看出

$\frac{\frac{1}{n-1}}{1}=\frac{x}{y}$

消去$y$可以得到$x=\frac{1}{n}$

这样我们又有一种n等分的方式

$tip:$如果要得到7等分，我们可以先折3等分再对折，从而由6等分得到7等分

References:

高中/选择题

Posted on 2022-07-23

首先厘清题意明确情形

对图形进行全面有序的分析

找出所求目标(正确或错误)

分析问题将题给条件进行转换

在空白处写出关键条件

对照原题标出数据

在草稿纸上进行化简计算

对照选项进行验证

若非常有把握就直接过

有困难就排除分析

大一/概率论/基本

Posted on 2022-07-23

概率论公理

我们说样本空间是无限可数的意味着其中的元素可以与正整数一一对应

样本空间$S$上的概率分布$\rm {Pr{}}$是一个从事件到实数的映射

记号

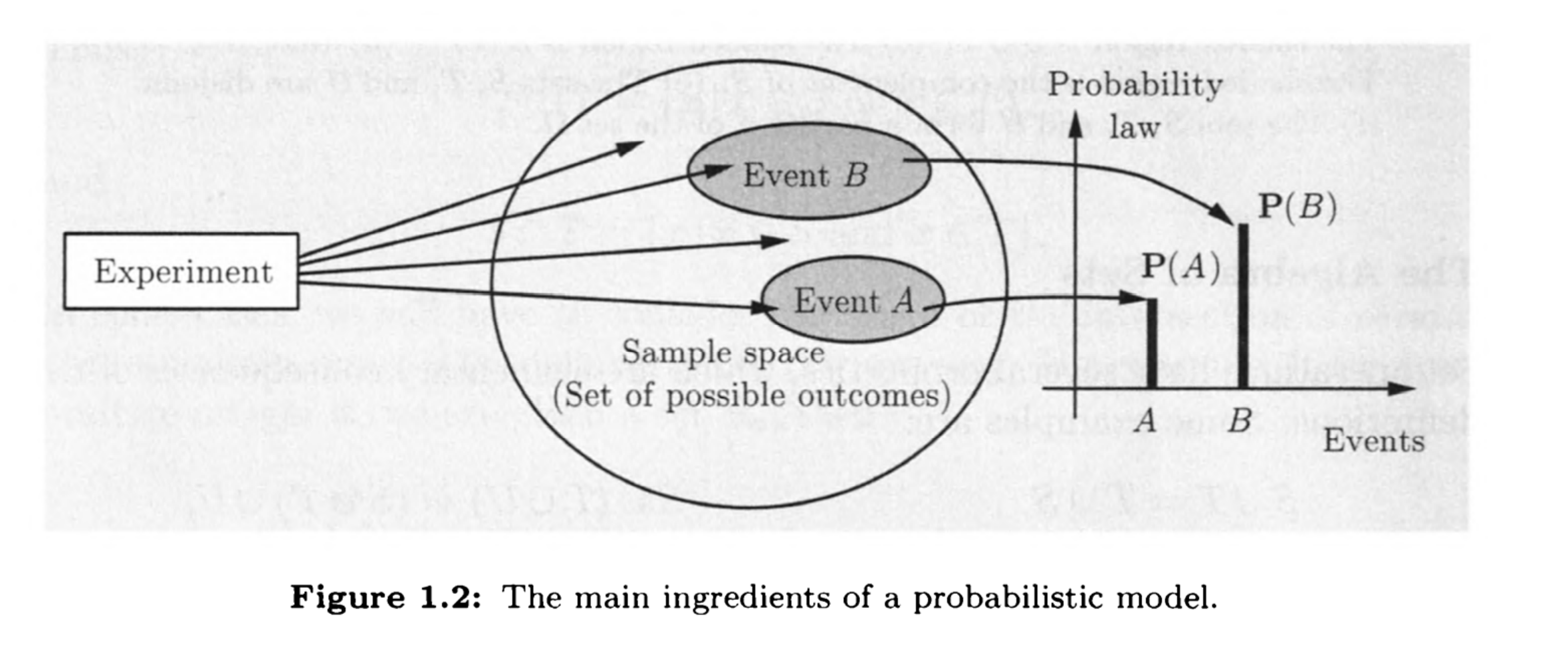
将事件$\text{Pr}({A})$简记为$\text{Pr}{A}$

事件可能有无数个，如掷硬币n次H

$\forall 事件A,\text {Pr}{A}\ge0$
$\text {Pr}{S}=1$
对两两互斥的事件，有
$\text {Pr}\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}=\text {Pr}\left\{s_{1}\right\}+\text {Pr}\left\{s_{2}\right\}+\cdots+\text {Pr}\left\{s_{n}\right\}\\ \text {Pr}\left\{\bigcup_{i}A_i\right\}=\sum_i\text {Pr}\{A_i\}$

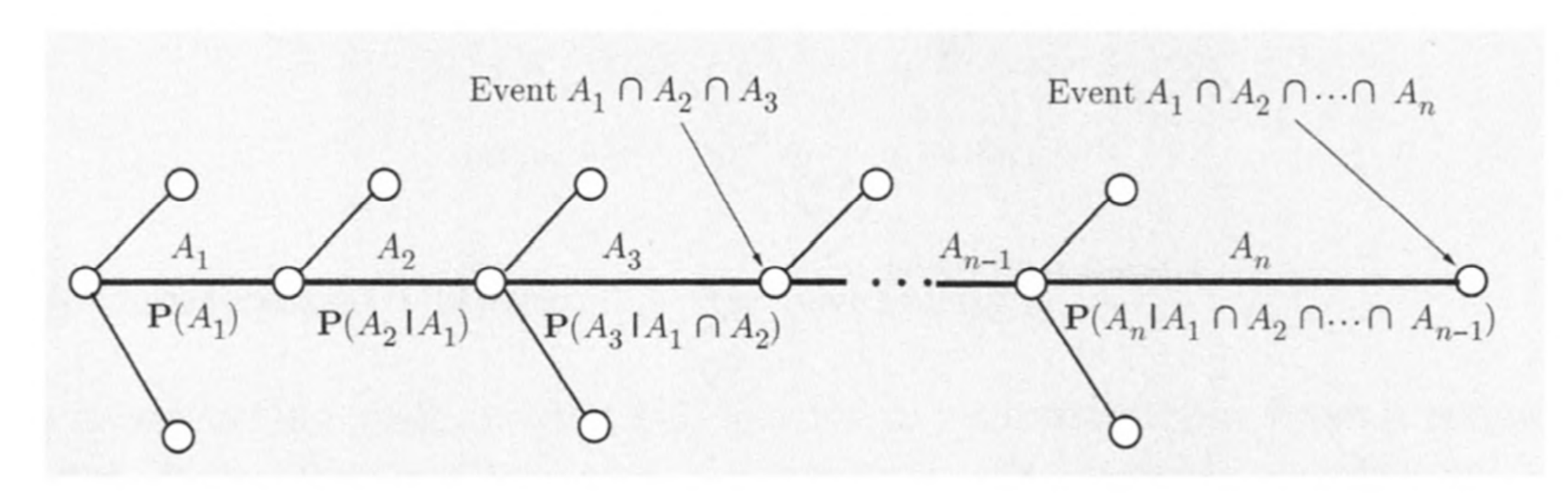
对于一个序列型的事件，可以用以下方式描述

模型

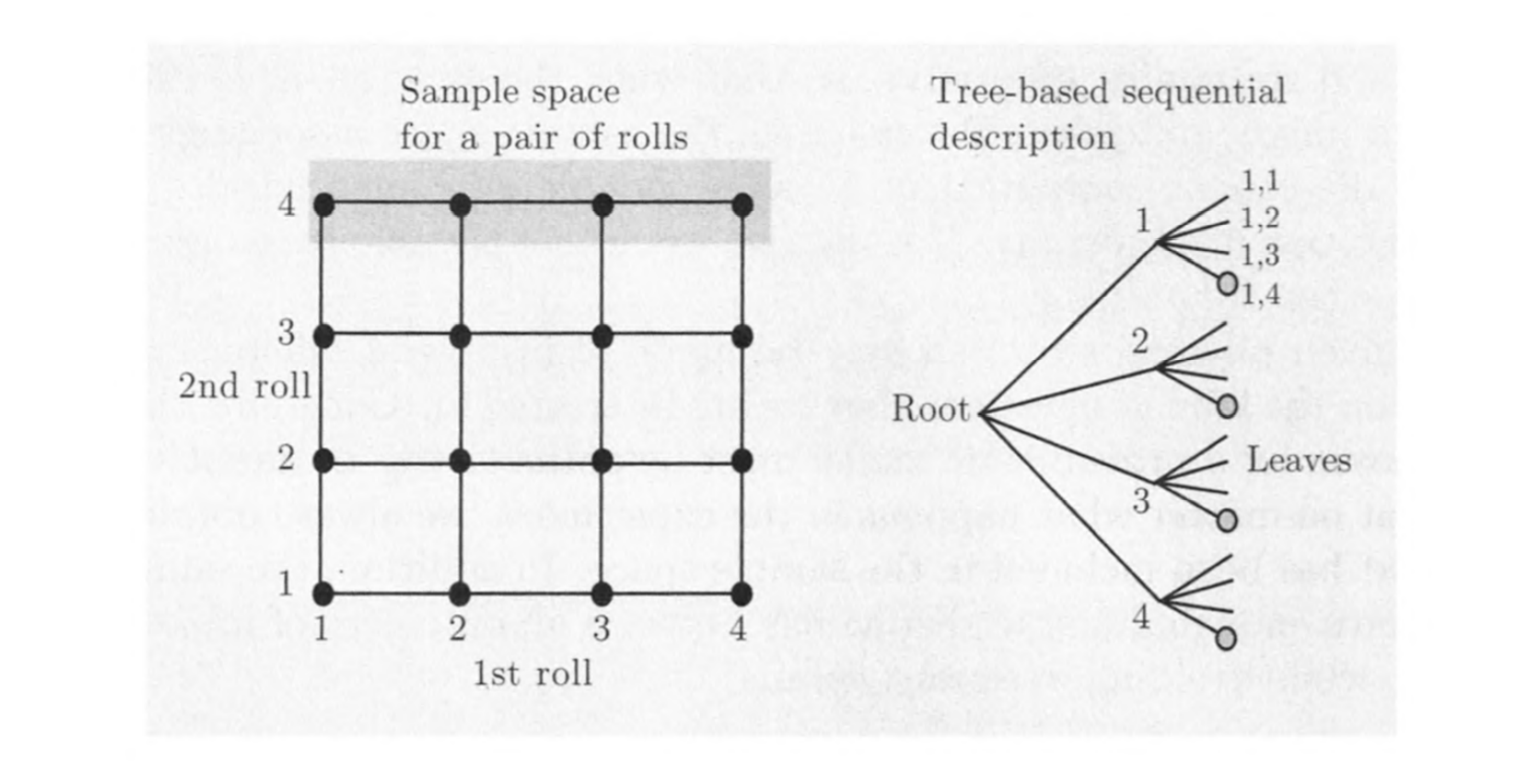
为了构建模型，我们需要考虑多个因素

The choice of a model often involves a tradeof be-tween accuracy, simplicity,and tractability.

但是不论多复杂的模型，对于某个特定的事件都有确定的概率

All conceivable questions have precise answers and it is only a matter of developing the skill to arrive at them.

离散模型

对于多个等概率事件

$\text {Pr}\{A\}=\frac{\text{number of elements of }A }{n}$

连续模型

样本空间可以用图形来表示

对于样本空间为

$\Omega=[0,1]$

对于某一个值，概率为0，只有考虑长度才有意义

$\text { If } A \subset B, \text { then } \text {Pr}\{A\} \leq \text {Pr}\{B\}$

容斥

$\begin{aligned}\text {Pr}\{A\cup B\}&=\text {Pr}\{A\}+\text {Pr}\{B\}-\text {Pr}\{A\cap B\}\\&\le\text {Pr}\{A\}+\text {Pr}\{B\}\end{aligned}$ $\text {Pr}\left\{\bigcup_{i}A_i\right\}\le\sum_i\text {Pr}\{A_i\}$

由德摩根律

$\text {Pr}\{A\cup C|B\}\le\text {Pr}\{A|B\}+\text {Pr}\{C|B\}$

离散概率分布

概率分布在有限或无限可数的样本空间，则该概率分布是离散的

$\text {Pr}\{A\}=\sum_{s\in A}\text {Pr}\{s\}$

若基本事件$s\in S$的概率为

$\text {Pr}\{s\}=1/|S|$

则称为$S$上的的均匀概率分布

条件概率

已知事件 $B$发生$\text {Pr}{B}\ne 0$，事件$A$的条件概率定义为

$\text {Pr}\{A|B\}=\frac{\text {Pr}\{A\cap B\}}{\text {Pr}\{B\}}$

需要从直观角度上理解

$\text {Pr}\{A|B\}+\text {Pr}\{A^c|B\}=1$

状态转移

$\mathbf{P}\left(\cap_{i=1}^{n} A_{i}\right)=\mathbf{P}\left(A_{1}\right) \cdot \frac{\mathbf{P}\left(A_{1} \cap A_{2}\right)}{\mathbf{P}\left(A_{1}\right)} \cdot \frac{\mathbf{P}\left(A_{1} \cap A_{2} \cap A_{3}\right)}{\mathbf{P}\left(A_{1} \cap A_{2}\right)} \cdots \frac{\mathbf{P}\left(\cap_{i=1}^{n} A_{i}\right)}{\mathbf{P}\left(\cap_{i=1}^{n-1} A_{i}\right)}$

独立

若

$\text {Pr}\{A\cap B\}=\text {Pr}\{A\}\text {Pr}\{B\}$

则称事件$A$和$B$是独立的，若$\text {Pr}{B}\ne 0$，则等价于

$\text {Pr}\{A|B\}=\Pr\{A\}(与B无关)$

若对于所有$1\le i < j\le n$，有

$\text {Pr}\{A_i\cap A_j\}=\Pr\{A_i\}\Pr\{A_j\}$

则称事件$A_1,A_2,\cdots,A_n$两两独立

若对这些事件的每一个$k$子集${ A{i_1},A{i2},\cdots,A{i_k}}$，其中$2\le k\le n$且$1\le {i_1}< {i_2}< \cdots< {i_k}\le n $，有

$\Pr\{ A_{i_1}\cap A_{i_2}\cap \cdots\cap A_{i_k}\}=\Pr\{ A_{i_1}\}\Pr\{ A_{i_2}\}\cdots\Pr\{ A_{i_k}\}$

则称这些事件相互独立

条件独立

$\text {Pr}\{A\cap B|C\}=\text {Pr}\{A|C\}\text {Pr}\{B|C\}\\ \Leftrightarrow\text {Pr}\{A| B\cap C\}=\text {Pr}\{A|C\}$

In words, this relation states that if is known to have occurred,the additional knowledge that B also occurred does not change the probability of A.

考虑事件A为第一次掷为H，B为第二次H，C为两次结果不同

$\text {Pr}\{A\cap B|C\}=0\\\text {Pr}\{A|C\}=\text {Pr}\{B|C\}=\frac12$

所以独立不代表条件独立

$\text {Pr}\{A\cap B\cap C\}=0$

则A，B两个独立事件不条件独立

全概率公式

将样本空间$\Omega$划分为两两独立的$n$个事件，且

$\bigcup_iA_i=\Omega$

则

$\Pr\{B\}=\sum_{i=1}^n\Pr\{B|A_i\}\Pr\{A_i\}$

贝叶斯定理

由

$\Pr\{A\cap B\}=\Pr\{A|B\}\Pr\{B\}=\Pr\{B|A\}\Pr\{A\}$

得

$\Pr\{A|B\}=\frac{\Pr\{B|A\}\Pr\{A\}}{\Pr\{B\}}$

对于$\Pr{B}$，因为可以划分，故

$\Pr\{B\}=\Pr\{B|A\}\Pr\{A\}+\Pr\{B|\overline{A} \}\Pr\{\overline{A} \}$

所

$\Pr\{A|B\}=\frac{\Pr\{B|A\}\Pr\{A\}}{\Pr\{B|A\}\Pr\{A\}+\Pr\{B|\overline{A} \}\Pr\{\overline{A} \}}$

贝叶斯定理常常用来由果导因，如抗原阳性是否代表感染新冠

$\Pr\{A_i|B\}=\frac{\Pr\{B|A_i\}\Pr\{A_i\}}{\Pr\{B|A_1\}\Pr\{A_1\}+\dots+\Pr\{B|A_n \}\Pr\{A_n \}}$

其中$\Pr{A_i|B}$为后验概率，$\Pr{A_i}$是先验概率

计数

分类加法计数原理，同一个阶段的不同方法可以相加

有N个阶段每个阶段有$n_i$个方式，则总方式为

$n_1n_2\cdots n_N$

排列数

$k-\text{permutations}=\frac{n!}{(n-k)!}$

组合数

$\left(\begin{array}{l}n\\k\end{array}\right)=\frac{n!}{(n-k)!k!}$

多项式定理

将n个元素分为$k$类，其中各为$n_i$个

$C_{n}^{n_{1}} C_{n-n_{1}}^{n_{2}} \ldots C_{n-n_{1}-\ldots-n_{k-1}}^{n_{k}}=\frac{n !}{n_{1} ! n_{2} ! \ldots n_{k} !}$ $\left(x_{1}+\ldots+x_{k}\right)^{n}=\sum_{n_{1}+\ldots+n_{k}=n}\left(\begin{array}{ccc} & n & \\ n_{1} & \ldots & n_{k} \end{array}\right) x_{1}^{n_{1}} x_{2}^{n_{2}} \ldots x_{k}^{n_{k}}$

大一/概率论/随机变量

Posted on 2022-07-23

随机变量

随机变量$X$是有限或无限可数样本空间$S$到实数的函数

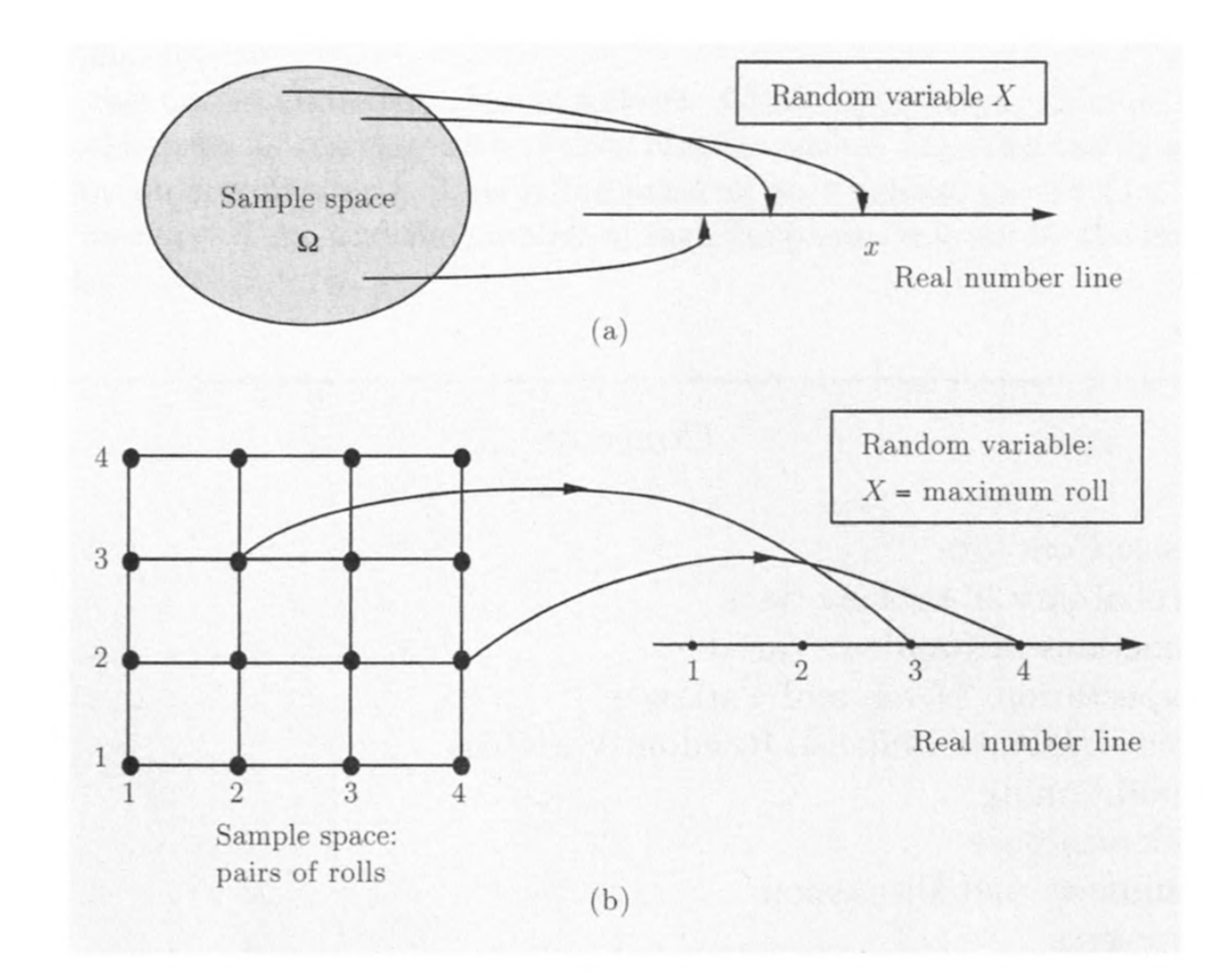
对于随机变量$X$和实数$x$，定义事件$X=x$为${s\in S,X(s)=x}$，因此

we will use upper case characters to denote random variables， and lower case characters to denote real numbers such as the numerical values of a random variable.

$\Pr\{X=x\}=\sum_{s\in S,X(s)=x}\Pr\{s\}$

对于随机变量，函数$p_X(x)=\Pr{X=x}$为$X$的概率质量函数PMF

PDF

特别的，对于连续随机变量也称为概率密度函数PDF

$\Pr\{X\in B\}=\int_Bf_X(x)\text{d}x$

归一化条件为

$\int_{-\infty}^{+\infty}f_X(x)\text{d}x=1$ $\Pr\{[x,x+\delta ]\}\approx f_X(x) \delta$

所以$f_X(x)$可以看成单位长度的概率

可以把这两种函数整合成一个函数

即为累积分布函数CDF(cumulative distribution function)

$F_x(x)=\text{Pr}\{X\le x\}=\begin{cases}\displaystyle\sum_{k\le x}p_X(k) \\\displaystyle\int_{-\infty}^xf_X(x)\text{d}x\end{cases}$

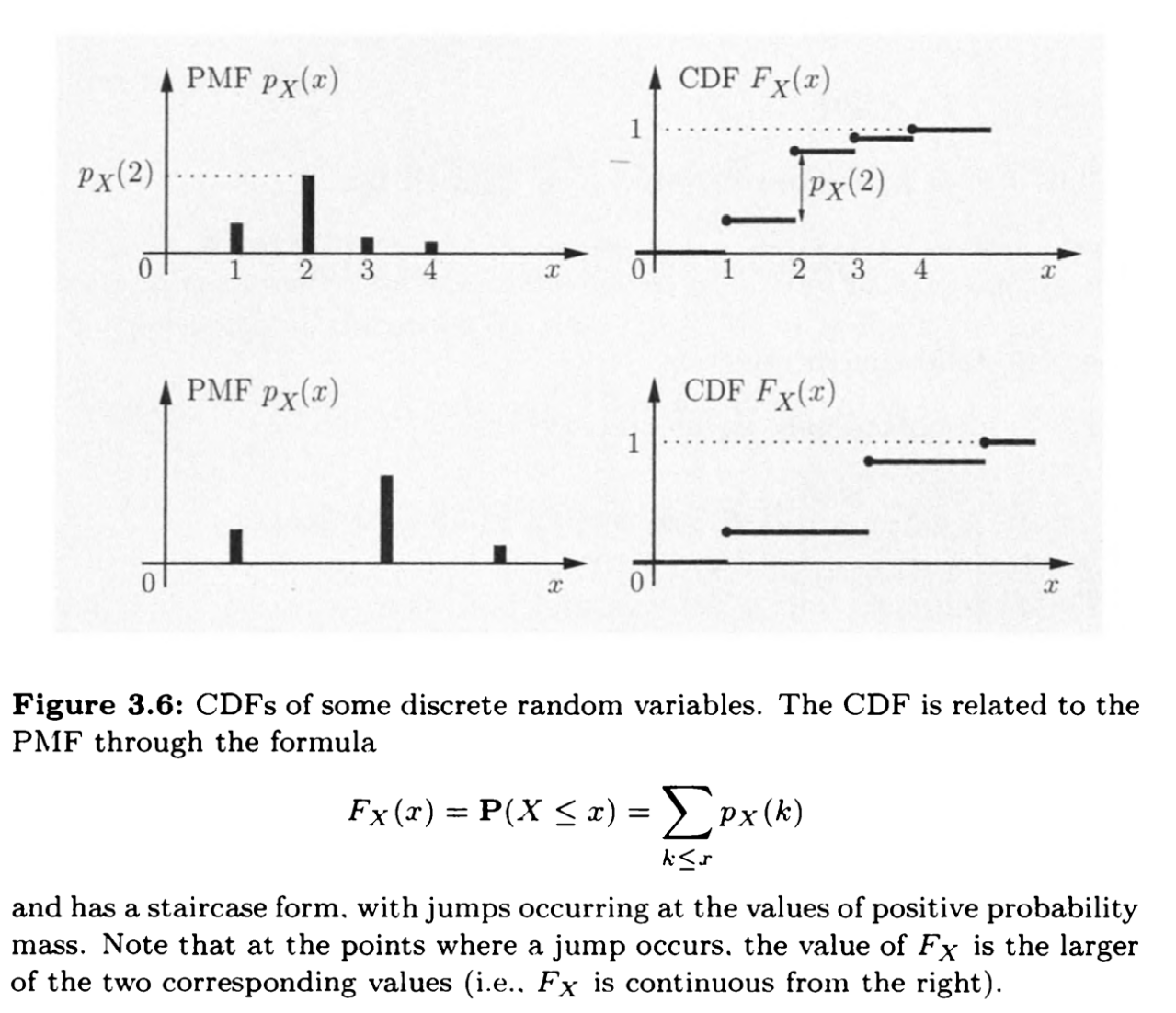
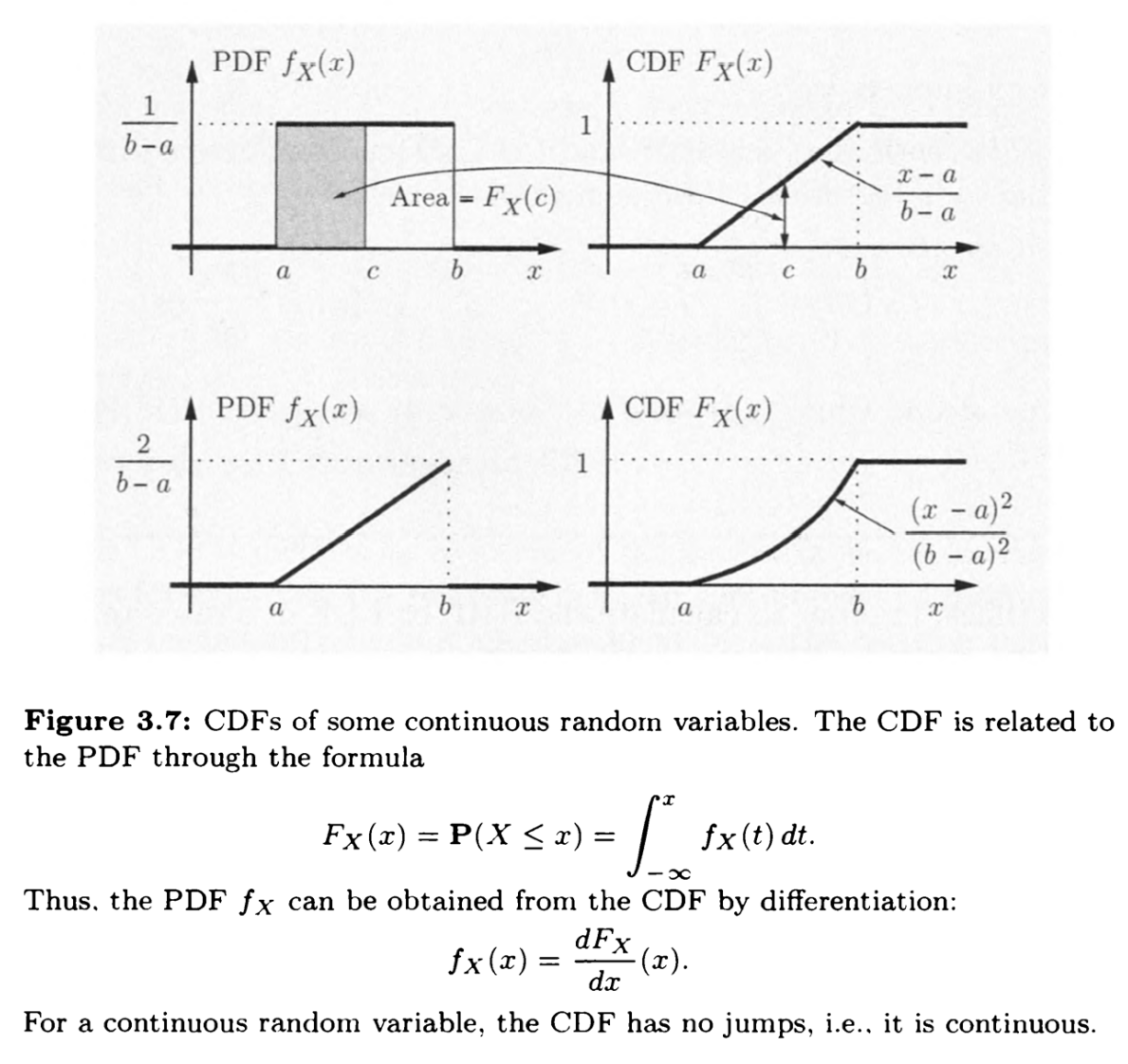
可以类比积分上限函数，通过差分和求导可以还原

若有若干个随机变量，即为多维随机变量

则有联合PMF

$p_{X,Y}(x,y)=\Pr\{X=x且Y=y\}\\ p_{X}(x)=\Pr\{X[1]=x[1],\cdots,X[d]=x[d]\}\\ \sum_{x[1]\in X_1}\sum_{x[2]\in X_2} \cdots\sum_{x[d]\in X_d}=1$

为$X$与$Y$的联合概率密度函数，性质同理，

如边缘$\rm PMF$

$\begin{aligned}\Pr\{Y=y\}&=\sum_x\Pr\{X=x且Y=y\}(y为定值)\\&=\sum _xp_{X,Y}(x,y)\end{aligned}\\$ $p_Z(z)=\sum_{\{z|z=g(x,y)\}}p_{X,Y}(x,y)\\ \text{E}[g(X, Y)]=\sum_{x} \sum_{y} g(x, y) p_{X, Y}(x, y)$

函数

$Y=g(X)\\p_Y(y)=\sum_{\{x|g(x)=y\}}p_X(x)$

边缘函数

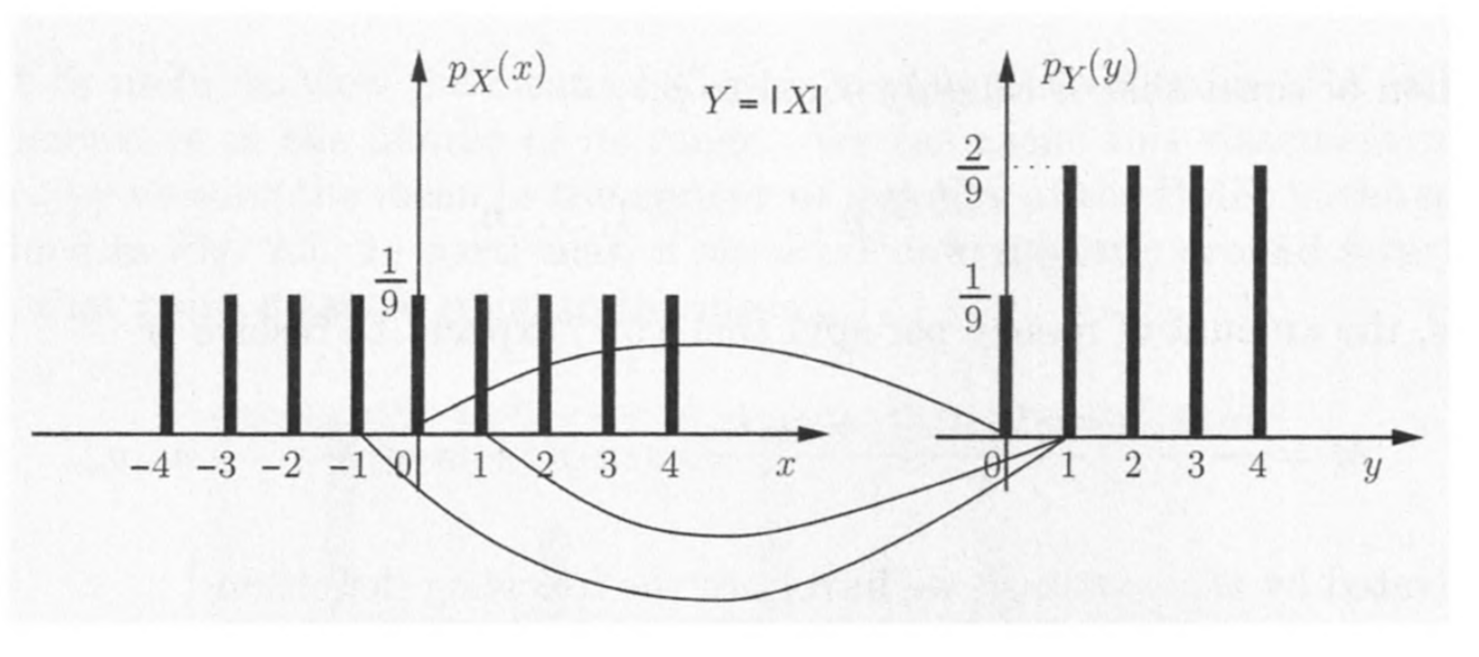
设$(X,Y)$的联合分布为$F(X,Y)$则

$F_X(x)=P(X\le x)$

为随机变量$X$的边缘分布函数

$f_X(x)=\int_{-\infty}^{+\infty}f(x,y)\text dy$

为边缘密度函数

利用定义可以求$Z=g(X,Y)$的分布

$F_Z(z)=\iint_{g(x,y)\le z}f(x,y)\text dx\text dy$

从而有

$f_Z(z)=\frac{\text d F_Z(z)}{\text d z}$

随机变量的期望值

$\text E[X]=\sum_xx\cdot\Pr\{X=x\}\\ \text E[g(X)]=\sum_xg(x)\cdot\Pr\{X=x\}\\$

对于连续的随机变量

$\text{E}[X]=\int_{-\infty}^{+\infty}xf_X(x)\text{d}x\\ \text{E}[g(X)]=\int_{-\infty}^{+\infty}g(x)f_X(x)\text{d}x$

期望的线性性质

$\text E\left[\sum_{i=1}^nX_i\right]=\sum_{i=1}^n\text E[X_i]\\\text E[aX+b]=a\text E[X]+b$

若相互独立，使用期望的定义得

$\text E[XY]=\text E[X]\text E[Y]$

方差

$\text{Var}[X]=\text{E}[(X-\text{E}[X])^2]=\text{E}[X^2]-\text{E}^2[X]\\ \text{Var}[aX+b]=a^2\text{Var}[X]$

对于连续的随机变量

$\text{Var}[X]=\int_{-\infty}^{+\infty}(x-\text{E}[X])^2f_X(x)\text{d}x\\$ $\text{Var}[X\pm Y]=\text{Var}[X]+\text{Var}[Y]\pm2E[(X-E[X])(Y-E[Y])]$

若相互独立

$\text{Var}[X\pm Y]=\text{Var}[X]+\text{Var}[Y]\\ \text{Var}[\sum_{i=1}^nX_i]=\sum_{i=1}^n\text{Var}[X_i]$ $\begin{aligned}\text{Var}[XY]&=\text{E}^2[Y]\text{Var}[X]+\text{E}[X^2]\text{Var}[Y]\\ &=\text{E}[Y]^2\text{Var}[X]+\text{E}^2[X]\text{Var}[Y]\\ &=\text{Var}[X]\text{Var}[Y]+\text{E}^2[Y]\text{Var}[X]+\text{E}^2[X]\text{Var}[Y] \end{aligned}$

标准差

$\sigma_X=\sqrt{\text{var}(X) }$

矩

随机变量使用概率密度函数描述，概率密度函数具有一个特性，称为 矩 Moment，矩是随机变量幂的期望。我们重点关注两种矩：

$k$阶原点矩，$\text E\left[ X^{k} \right]$
$k$阶中心距，$\text E\left[ (X-\text E[x]) \right]^{k}$

随机矩阵

对于矩阵$\tilde{X}(d_1,d_2)$，其均值为

$\mathrm{E}(\tilde{X}):=\begin{bmatrix}\mathrm{E}\left(\tilde{X}[1,1]\right)&\mathrm{E}\left(\tilde{X}[1,2]\right)&\cdots&\mathrm{E}\left(\tilde{X}[1,d_2]\right)\\\mathrm{E}\left(\tilde{X}[2,1]\right)&\mathrm{E}\left(\tilde{X}[2,2]\right)&\cdots&\mathrm{E}\left(\tilde{X}[2,d_2]\right)\\&&\cdots\\\mathrm{E}\left(\tilde{X}[d_1,1]\right)&\mathrm{E}\left(\tilde{X}[d_1,2]\right)&\cdots&\mathrm{E}\left(\tilde{X}[d_1,d_2]\right)\end{bmatrix}$

线性性质

$\mathrm{E}(A\tilde x+B)=A\mathrm{E}(\tilde x) +B$

独立

若对于一切$x,y$

$F(x,y)=F_X(x)F_Y(y)$

则称两随机变量相互独立

卷积

$Z=X+Y$

则有

$f_Z(z)=\int_{-\infty}^\infty f_X(x)f_{Y}(z-x)\text dx$

协方差

$\mathbf{Cov}(X,Y)=E\{[X-E(X)][Y-E[Y]]\}$

类比有

$\mathbf{Cov}(X,Y)=E(XY)-E(X)E(Y)$

条件

conditional PMF

$p_{X|A}=\frac{\text{Pr}\{\{X=x\}\cap A \}}{\text{Pr}\{A\}}$

可以将A推广为一个随机变量

$p_{X|Y}(x,y)=\frac{p_{X,Y}(x,y)}{p_Y(y)}$

$\sum_{x} p_{X \mid Y}(x \mid y)=1$

分布

离散

几何分布

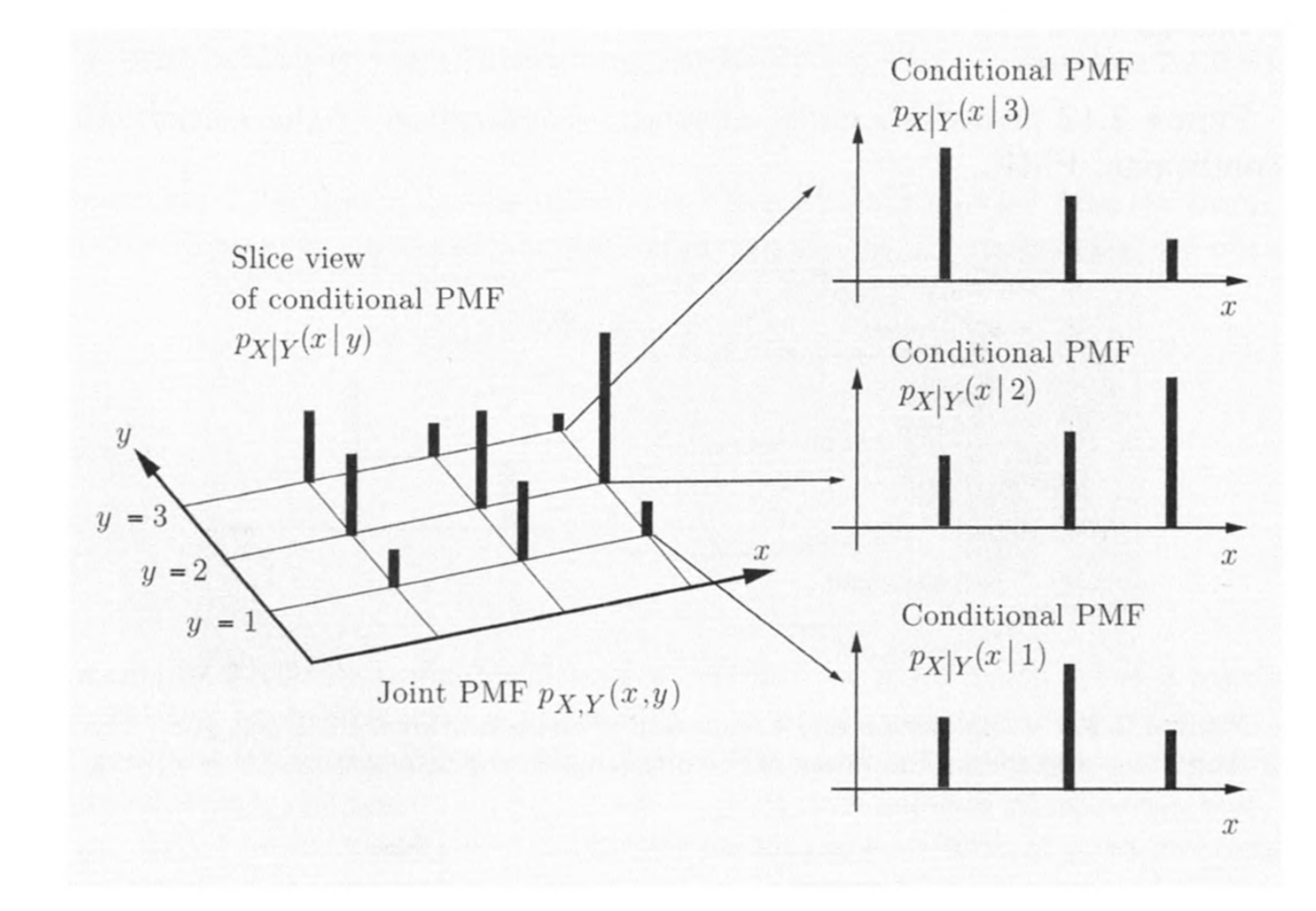
前面一直没有成功直到第n次才成功

$\Pr\{X=k\}=(1-p)^{n-1}p\\ \text E[x]=\sum_{k=1}^\infty(1-p)^{k-1}pk=1/p$

二项分布

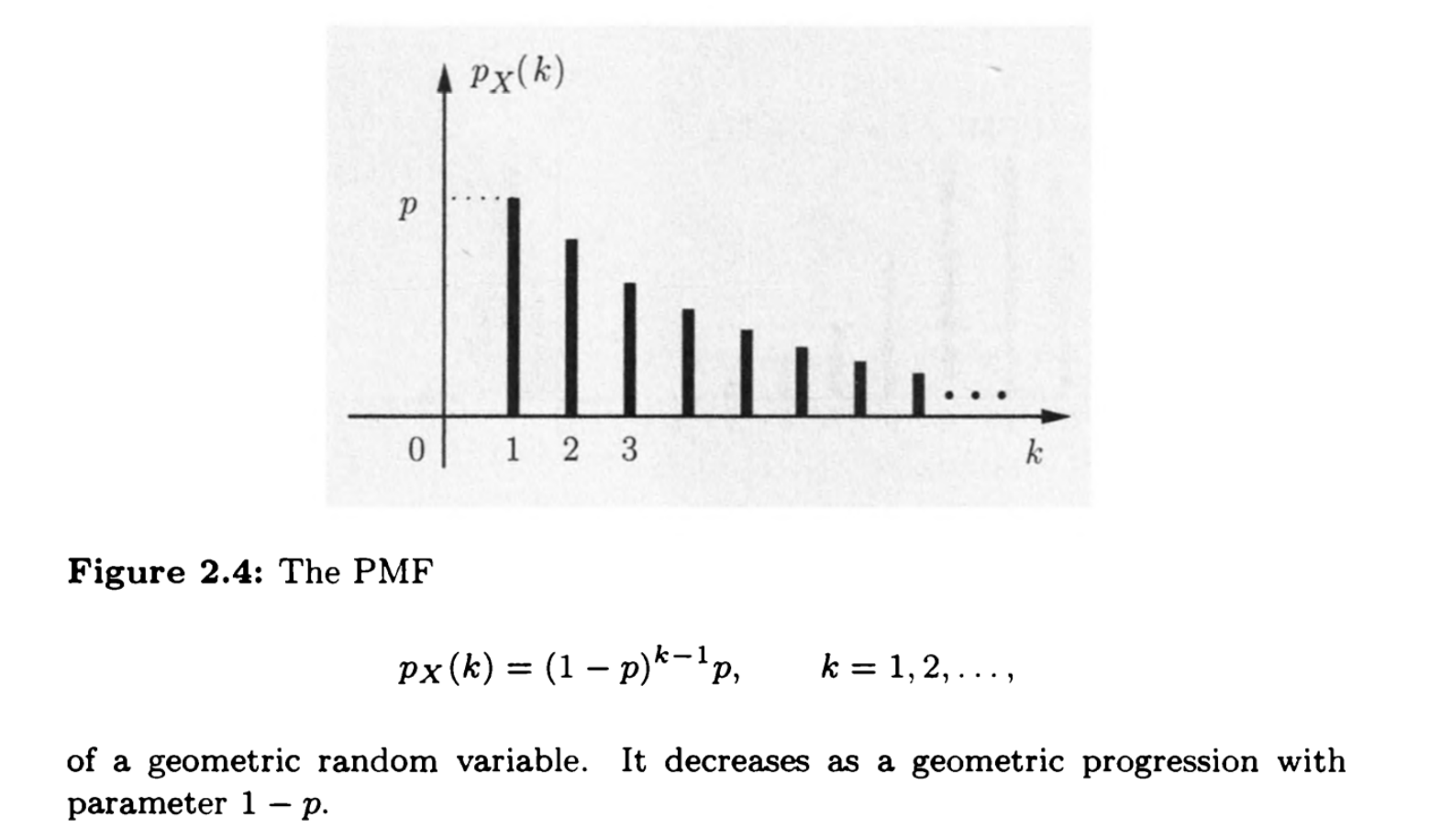
区别于国内表达，组合数记为

$\left(\begin{array}{l}n\\k\end{array}\right)=C_n^k$

读作$n$取$k$

$\Pr\{X=k\}=\left(\begin{array}{l}n\\k\end{array}\right)p^k(1-p)^{n-k}\\ \text E[X]=np\\ \text{Var}[X]=np(1-p)$

泊松分布

在某段时间内事件发生的概率为

$p=\lambda t$

则$t=0\to1$发生的次数可以表示为

$p_X(k)=e^{-\lambda}\frac{\lambda^k}{k!}\\ \sum_{k=0}^{\infty} e^{-\lambda} \frac{\lambda^{k}}{k !}=e^{-\lambda}\left(1+\lambda+\frac{\lambda^{2}}{2 !}+\frac{\lambda^{3}}{3 !}+\cdots\right)=e^{-\lambda} e^{\lambda}=1\\$

连续

均匀分布

$f_X(x)=\begin{cases}\frac{1}{b-a},&a\leq x\leq b,\\0,&\text{otherwise,}\end{cases}$

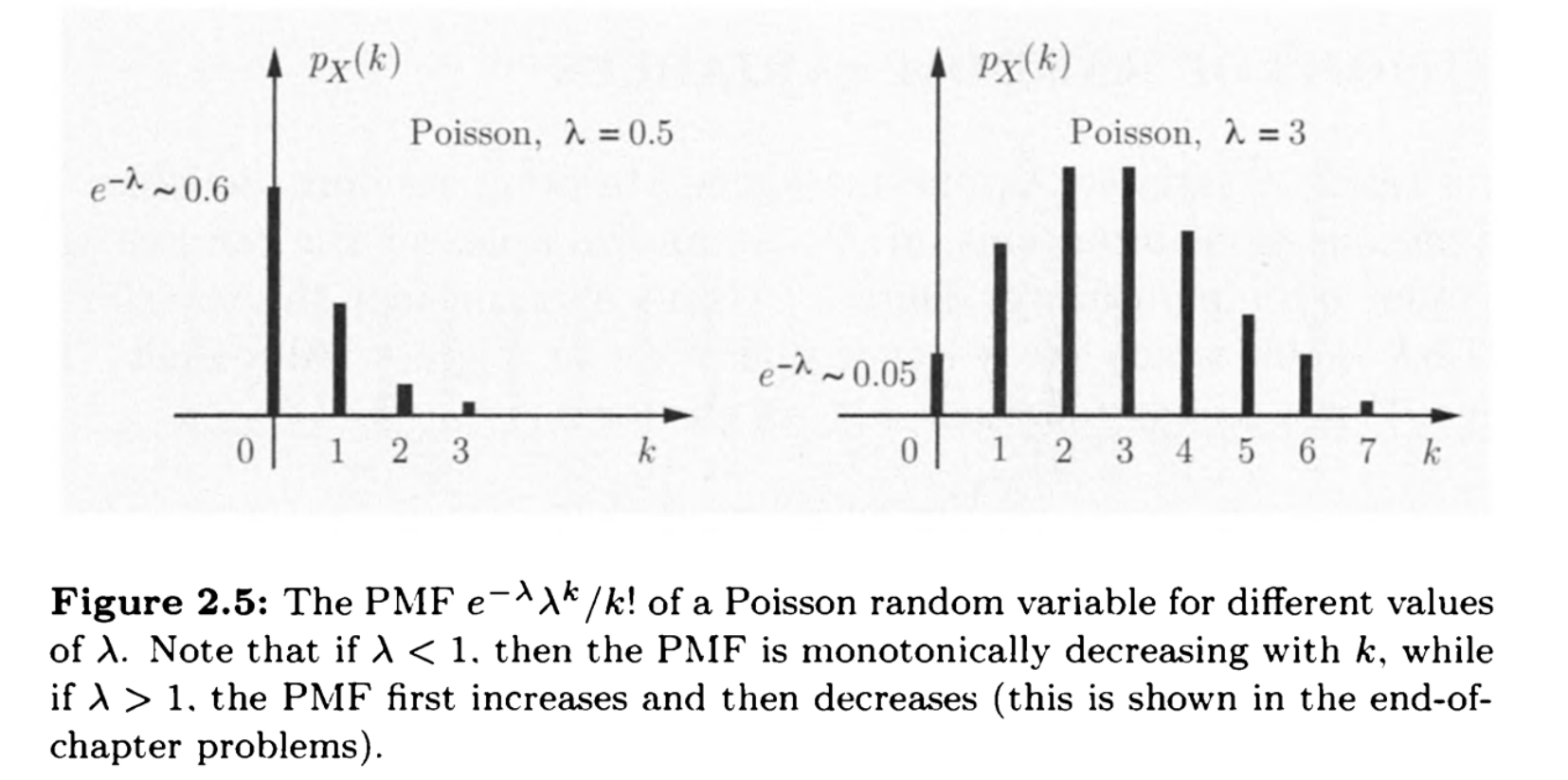
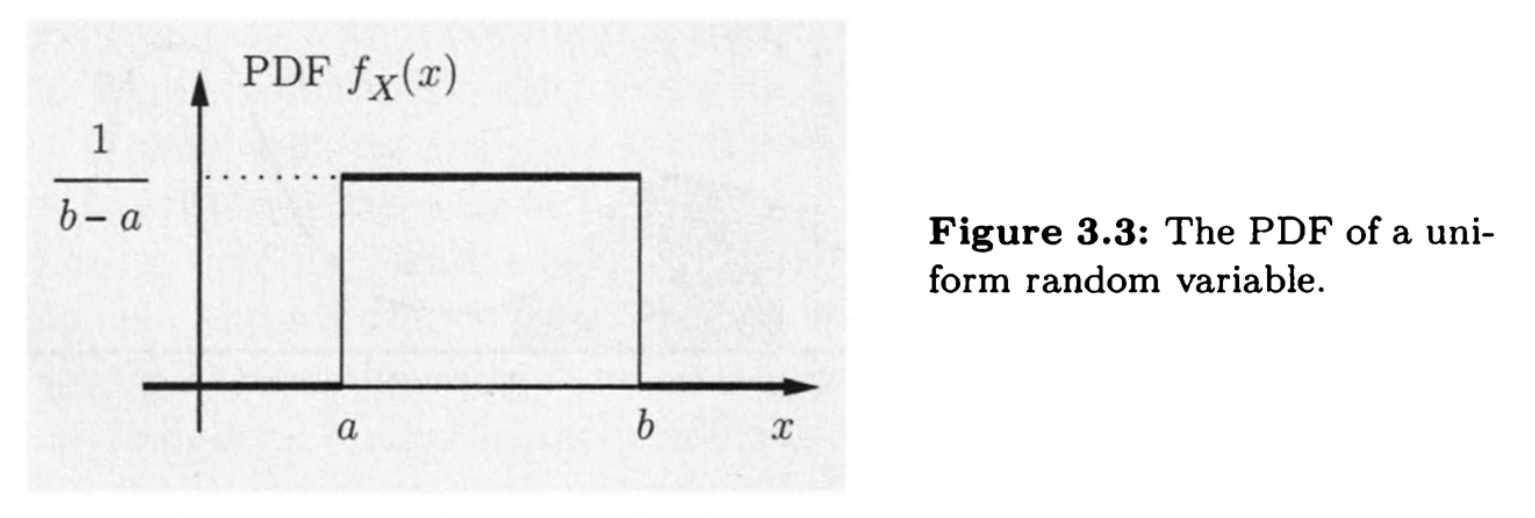
记为$X\sim U(a,b)$

则可以写出分布的期望和方差

$\mathbf{E}[X]=\frac{a+b}{2}\\ \mathbf{Var}[X]=\frac{(b-a)^2}{12}$

指数分布

$f_{X}(x)=\left\{\begin{array}{ll} \lambda e^{-\lambda x}, & \text { if } x \geq 0 \\ 0, & \text { otherwise } \end{array}\right.$

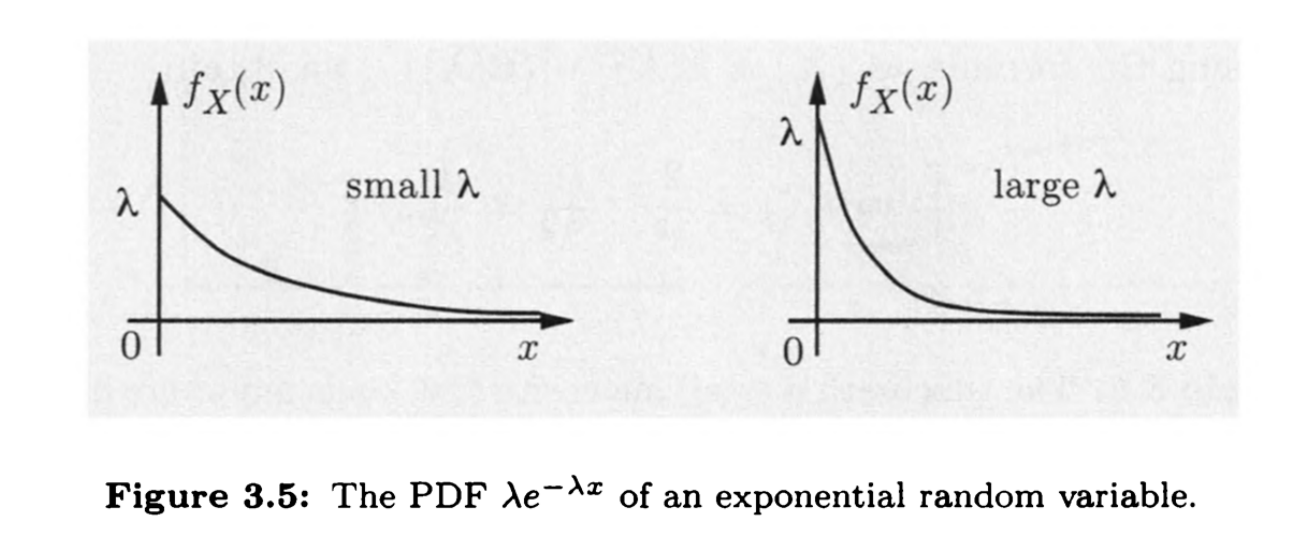
记为$X\sim E(\lambda)$

其中$\lambda$是参数可以用来调控均值，这个模型用途很广

类似与几何分布的情况，只不过用到了泊松分布的假设

$\mathbf{E}(X)=\frac1\lambda,\text{var}=\frac1{\lambda^2}$

正态分布

自然界许多现象都遵循 正态分布 Normal Distribution。正态分布又称为 高斯分布 Gaussian Distribution （纪念著名数学家卡尔·弗莱德利希·高斯），其表达式如下：

$f \left( x; \mu , \sigma ^{2} \right) = \frac{1}{\sqrt[]{2 \pi \sigma ^{2}}}e^{\frac{- \left( x- \mu \right) ^{2}}{2 \sigma ^{2}}}$

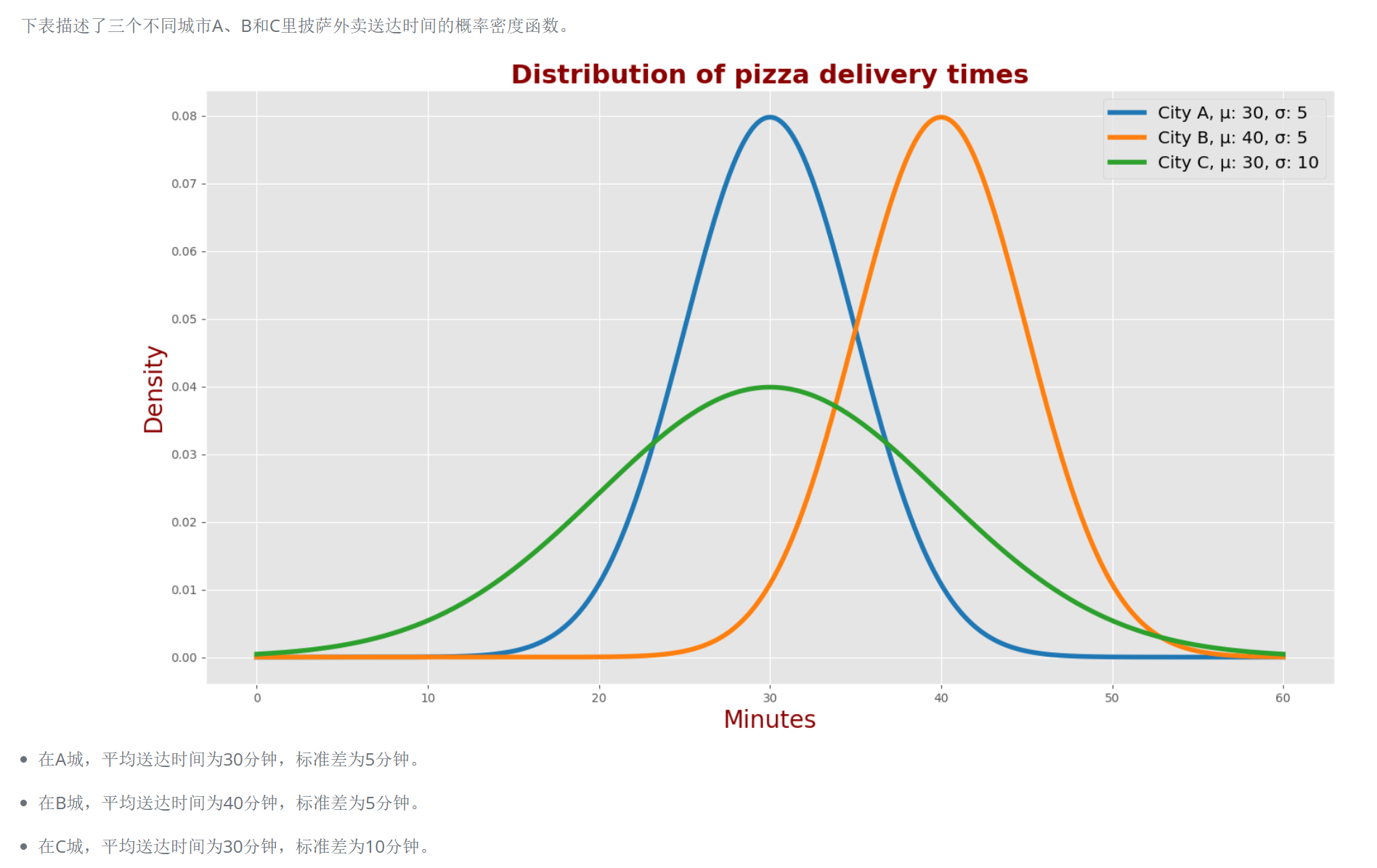
记为$X\sim N(\mu,\sigma^2)$，若$\mu=\sigma=1$则为标准正态分布

$f_X(x)=\frac1{\sqrt{2\pi}\sigma}e^{-(x-\mu)^2/2\sigma^2}$ $\text{E}[X]=\mu, \quad \operatorname{Var}(X)=\sigma^{2}$

可以利用标准正态分布函数来计算概率

$P(a<X<b)=\Phi\left(\frac{b-\mu}\sigma\right)-\Phi\left(\frac{a-\mu}\sigma\right)$

可加性

$kX+lY\sim N(k\mu_1+l\mu_2,k^2\sigma_1^2+l^2\sigma_2^2)$

分位数

$\Phi(u_p)=P(X\le u_p)=p$

则称$u_p$为标准正态分布的$p$分位数

$\Phi(-u_p)=1-p$

最值

$X_i$服从同一分布，则

$U=\max\{X_i\},V=\min\{X_i\}\\ f_U(x)=n[f(x)]^{n-1}f(x)\\ f_V(x)=n[1-f(x)]^{n-1}f(x)$

数字特征

偏度

$\beta_s(X)=\frac{E\{[X-\mathbf E(X)]^3\}}{[\mathbf{Var}[X]]^{3/2}}$

$\beta_s(X)<0$为左偏，左侧有较长的尾部，反之同理

峰度

$\beta_k(X)=\frac{E\{[X-\mathbf E(X)]^4\}}{[\mathbf{Var}[X]]^{2}}-3$

峰度和正态分布比较

变异系数

$C_v(X)=\frac{\sigma(X)}{|E(X)|}$

用均值标准化

中心极限定理

切比雪夫不等式，若$E(X^2)<+\infty$

$P(|X-E(X)|\ge \varepsilon)\le\frac{\mathbf{Var}(X)}{\varepsilon^2}$

马尔可夫不等式，若$E(|X|^p)<+\infty$

$P(|X|\ge \varepsilon)\le\frac{E(|X|^p)}{\varepsilon^p}$

样本均值

$\overline{X}=\frac1n\sum_{i=1}^nX_i\sim N\left(\mu,\frac{\sigma^2}n\right)\\ \overline{Y_n}=\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\sim N(0,1)$

或者

$\sum_{i=1}^nX_i\sim N\left(n\mu,n\sigma^2\right)$

$\chi ^2$分布

若$X_i$服从标准正态，则$U$服从自由度为$n$的$\chi ^2$分布

$U=\sum_{i=1}^nX_i^2\sim\chi^2(n)\\ \mathbf E(U)=n,\mathbf{Var}(U)=2n$

样本方差

$S^2=\frac1{n-1}\sum_{i=1}^n(X_i-\overline X)^2\\\frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)$

$\overline X$和$S^2$相互独立

可加性

$U_1\sim \chi^2(m),U_2\sim \chi^2(n)\\ U_1+U_2\sim \chi^2(m+n)$

$t$分布

若$X\sim N(0,1),Y\sim \chi^2(n)$

$T= \frac{X}{\sqrt{Y/n}}\sim t(n)$

F分布

$U\sim\chi^2(m),V\sim\chi^2(n) \\F=\frac{U/m}{V/n}\sim F(m,n)$

参数估计

矩估计

用样本矩来估计总体矩

$a_k=\frac1n\sum_{j=1}^nx_j^k$

最大似然估计

$L(\theta)=\prod_{i=1}^nf(x_i;\theta)$

最大化

$\frac{\text d}{\text d\theta }\ln L(\theta)=0$

评选标准

无偏

$E[\hat{\theta}(X_i)]=\theta$

渐近无偏

$\lim_{n\to\infty}E[\hat{\theta}(X_i)]=\theta$

相合

无偏或渐近无偏且

$\lim_{n\to\infty}\mathbf{Var}[\hat{\theta}(X_i)]=0$

置信区间

枢轴变量

$G=\frac{\sqrt{n}(\overline{X}-\mu)}\sigma\sim N(0,1)$

若方差已知，双侧

$\left[\overline{X}-u_{1-\frac{\alpha}{2}}\frac{\sigma }{\sqrt{n}} , \overline{X}+u_{1-\frac{\alpha}{2}}\frac{\sigma }{\sqrt{n}}\right]$

单侧

$\left[\overline{X}-u_{1-\alpha}\frac{\sigma }{\sqrt{n}} , +\infty\right)$

方差未知，用样本来估计

$\left[\overline{X}-t_{1-\frac{\alpha}{2}}(n-1)\frac{S }{\sqrt{n}} , \overline{X}+t_{1-\frac{\alpha}{2}}(n-1)\frac{S }{\sqrt{n}}\right]$

方差置信区间

$\frac{1}{\sigma^2}\sum\limits_{i=1}^n(X_i-\mu)^2 \sim \chi^2(n)$

可得

$\left[\frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{1-\frac{\alpha}{2}}(n)} , \frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{\frac{\alpha}{2}}(n)}\right]$

若方差未知则

$\left[\frac{(n-1)S^2}{\chi^2_{1-\frac{\alpha}{2}}(n-1)} , \frac{(n-1)S^2}{\chi^2_{\frac{\alpha}{2}}(n-1)}\right]$

大一/高数/曲率

Posted on 2022-07-23

预备知识

曲线光滑，有连续转动的切线

$f(x)=\begin{cases}x=x(t),\\y=y(t)\end{cases}\\ \exists x'(t),y'(t)\in C(\alpha,\beta)\\ x'(t)^2+y'(t)^2\ne0$

充分条件：导函数连续

弧微分公式

$\begin{aligned} s&=\int_{\alpha}^{\beta}\sqrt{x'(t)^2+y'(t)^2}\text{d}t\\ &=\int_{a}^{b}\sqrt{1+y'^2}\text{d}x\\ &=\int_{\alpha}^{\beta}\sqrt{\rho^2(\varphi)+\rho'^2(\varphi)}\text{d}\varphi \end{aligned}$ $\\ \text ds=\sqrt{1+y'^2}\text dx$

曲率

平均曲率

$\overline{K}=\left|\frac{\Delta \alpha}{\Delta s}\right|$

曲线$C$在$M$处的曲率

$K=\lim_{\Delta s \rightarrow0}\left|\frac{\Delta \alpha}{\Delta s}\right|=\left|\frac{\text d\alpha}{\text d s}\right|$ $K=\frac{|y''|}{(1+y'^2)^{3/2}}\approx |y''|$

曲率圆

$\rho=\frac1K$

则$\rho$为曲线在该点处的曲率半径

曲率圆的中心为该点处的曲率中心

大一/高数/积分表

Posted on 2022-07-23

基本积分表

$\text{Newton-Leibniz formula} \\ \int_a^bf(x)\mathrm dx =\left[F(x)\right]^b_a=F(b)-F(a)$ $\int k\text dx=kx+C\\ \int x^\mu\text dx=\frac{x^{\mu+1}}{\mu+1}+C(\mu\ne-1)\\ \int \frac{\text dx}{x}=\ln|x|+C\\ \int \frac{\text dx}{1+x^2}=\arctan x+C\\ \int \frac{\text dx}{\sqrt{1-x^2}}= \arcsin x+C$ $\int \cos x\text dx=\sin x +C\\ \int \sin x\text dx=-\cos x+C\\ \\\int \frac{\text dx}{\cos^2x}=\int\sec^2x=\tan x+C\\ \int \frac{\text dx}{\sin^2x}=\int\csc^2x=-\cot x+C\\ \\ \int \sec x\tan x\text dx=\sec x+C$ $\int \csc x \cot x\text dx=-\csc x+C\\ \int e^x=e^x+C\\\int a^x\text dx=\frac{a^x}{\ln a}+C\\$

拓展公式

$\int \frac{\text dx}{a^2+x^2}=\frac1a \arctan \frac xa+C\\ \int \frac{\text dx}{x^2-a^2}=\frac1{2a}\ln\left|\frac{x-a}{x+a}\right|+C\\ \int \frac{\text dx}{\sqrt{a^2-x^2}}= \arcsin \frac xa +C\\ \int \frac{\text dx}{\sqrt{a^2+x^2}}=\ln (x+\sqrt{x^2+a^2})+C\\ \int \frac{\text dx}{\sqrt{x^2-a^2}}=\ln |x+\sqrt{x^2-a^2}|+C\\$ $\int\tan x\text{d}x=-\ln |\cos x|+C\\ \int\cot x\text{d}x=\ln |\sin x|+C\\ \int\sec x\text{d}x=\ln |\sec x+\tan x|+C\\ \int\csc x\text{d}x=\ln |\csc x-\cot x|+C\\ \int \sinh x\text{d}x=\cosh x +C\\ \int \cosh x\text{d}x=\sinh x +C\\ \int x\cos x=x\sin x +\cos x +C$

常见凑微分公式

$a\text{d}x=\text{d}(ax)\\ 2x\text{d}x=\text{d}x^2\\ e^x\text{d}x=\text{d}e^x\\ \frac {e^x}{2\sqrt{1+e^x}}\text{d}x=\text{d}\sqrt{1+e^x}\\ e^x+e^{-x}\text{d}x=\text{d}(e^x-e^{-x})\\ \frac {x}{\sqrt{1+x^2}}\text{d}x=\text{d}\sqrt{1+x^2}$

Shiwei Pan

Open your eyes,look up to the skies

GitHub LinkedIn