大三/控制系统分析

时域分析

时域瞬态响应

时间响应，在数学上就是系统动力学方程的解

一阶系统

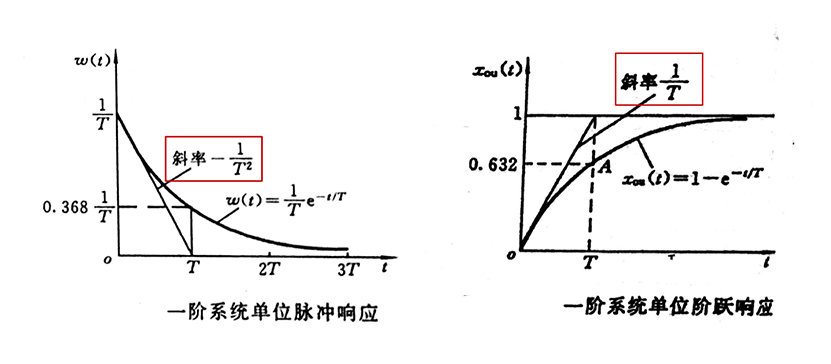
$t_s$为调整时间$3T\to 95\%,4T\to98\%$

一阶系统在阶跃输入下达到稳态的 $(1-\Delta)$ 时所用的时间 （ $\Delta$ 为容许误差）

$t_s$ 反应系统的快速性，T越大，调整时间越大，响应速度越慢

二阶系统

对 $G(s)=\frac{\omega_n^2}{s^2+2\xi\omega_n s+\omega_n^2}$ 来说：

特征方程：${s^2+2\xi\omega_n s+\omega_n^2}$

特征根：$s=\xi\omega_n\pm\omega_n\sqrt{1-\xi^2}$

• $\omega_n$ 为无阻尼固有频率，令 $\omega_d=\omega_n\sqrt{1-\xi^2}$ ，称为有阻尼固有频率
• $\xi=0$ ，系统为无阻尼系统，等幅振荡
• $0<\xi<1$ ，系统为欠阻尼系统，振荡收敛
• $\xi=1$，系统为临界阻尼系统，不振荡收敛
• $\xi>1$ ，系统为过阻尼系统，不振荡收敛

• 上升时间$t_r$ ：系统第一次到达稳态的时间

• 峰值时间$t_p$：系统第一次到达峰值的时间

• 最大超调量$M_p$：(峰值 - 稳态)/峰值%

• 调整时间$t_s$，当 $0<\xi<0.7$ 时

• $\xi$ 主要与震荡性（稳定性）正相关，$\omega_n$ 主要与快速性正相关。
• 系统的响应速度往往与震荡性能之间是矛盾的

稳态响应

对于一阶惯性系统，输入正弦信号$\sin(\omega t)$

$$U_o(s)=\frac1{Ts+1}\frac{\omega}{s^2+\omega^2}$$

分解

$$U_o(s)=\frac{T^2\omega}{1+T^2\omega^2}\frac1{Ts+1}+\frac1{Tj\omega+1}\frac{\omega}{s^2+\omega^2}$$

根据时移特性拉氏反变换，得到

$$u_o(t)=\frac{T\omega}{1+T^2\omega^2}e^{-\frac tT}+\frac1{\sqrt{(\omega T)^2+1}}\sin(\omega t-\arctan(\omega T))$$

所以稳态之后的信号也为正弦，幅值和相位的求法是把$s=j\omega$带入传递函数

$$G(j\omega)=U(\omega)+jV(\omega)$$

从而有时频特性和相频特性

$$\begin{cases}A(\omega)=\sqrt{[U(\omega)]^2+[V(\omega)]^2}\\ \phi(\omega)=\arctan\left[\frac{V(\omega)}{U(\omega)}\right]\end{cases}$$

频域分析

乃氏图

根据上面的每个$\omega$的幅值和相位可以确定一个点，绘制纵$0\to \infty$的曲线即为奈奎斯特图。

绘制

用极限的方法

$$\omega\to+\infty,G(j\omega)=0\angle-90^\circ$$

或者复数相乘，模相乘辐角相加原理，用常见的叠加得到

伯德图

即对数坐标图，纵坐标取对数，横坐标采用10倍频程比值缩放$\text{(dec)}$

（坐标轴仍任显示原值，只是计算斜率时使用）

$$n(\text{dB})=20\lg N\\ \omega'=\lg \omega$$

斜率

$$[-40]=40\text{dB/dec}=\frac{L-0}{\lg5-\lg1}$$

绘制

可以直接用斜率近似计算，也可以利用

$$\left|\frac{j\omega\tau+1}{j\omega T+1}\right|=\frac{\sqrt{(\omega\tau)^2+1}}{\sqrt{(\omega T)^2+1}}$$

直接计算关键点

常见的环节

比例环节

比例环节的频率特性是与频率无关的常数，在奈奎斯特图上表现为实轴上一个点，在伯德图中表现为与频率无关的两条直线

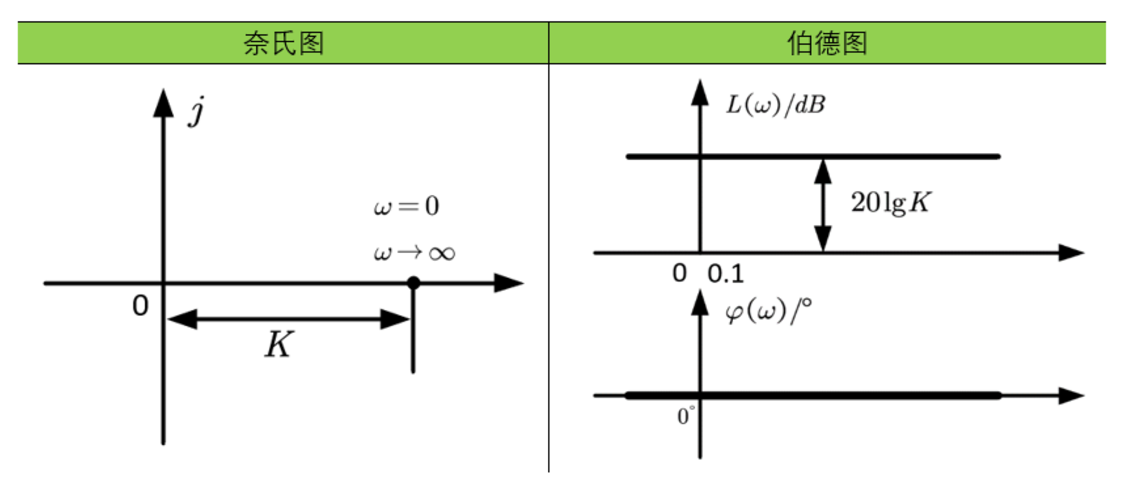
积分环节

积分环节的输出量是其输入量对时间的积分。奈奎斯特图是虚轴上从负无穷到原点的一条直线，相角恒为$-90^\circ$。对数幅频特性是一条$[-20]$斜率的直线，相角保持$-90^\circ$不变。

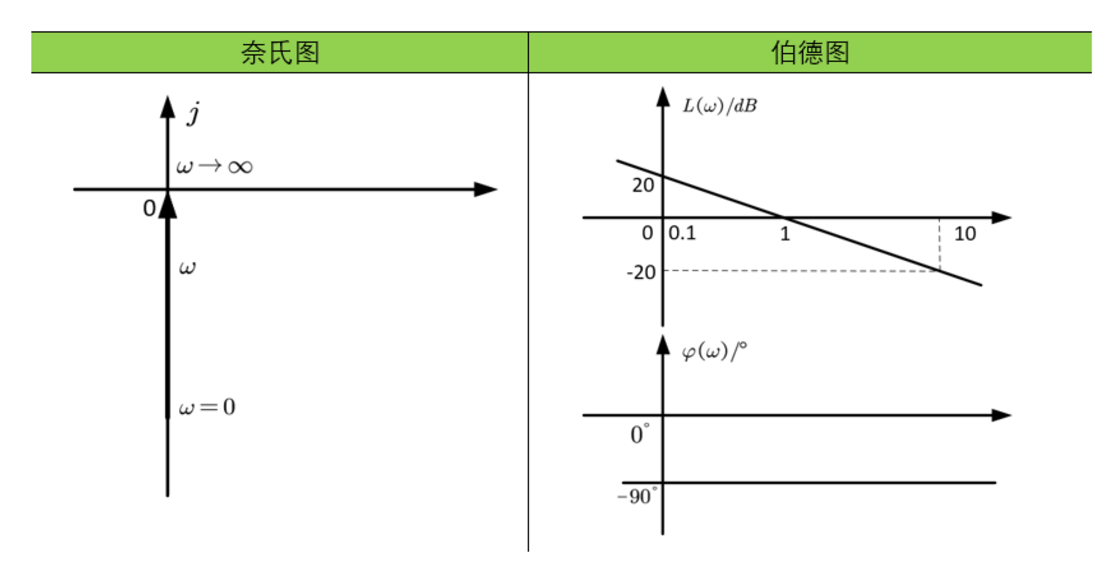
微分环节

微分环节的输出量是其输入量对时间的微分。奈奎斯特图是虚轴上从原点到正无穷的一条直线，相角恒为90°。对数幅频特性是一条$[+20]$斜率的直线，相角保持90°不变。

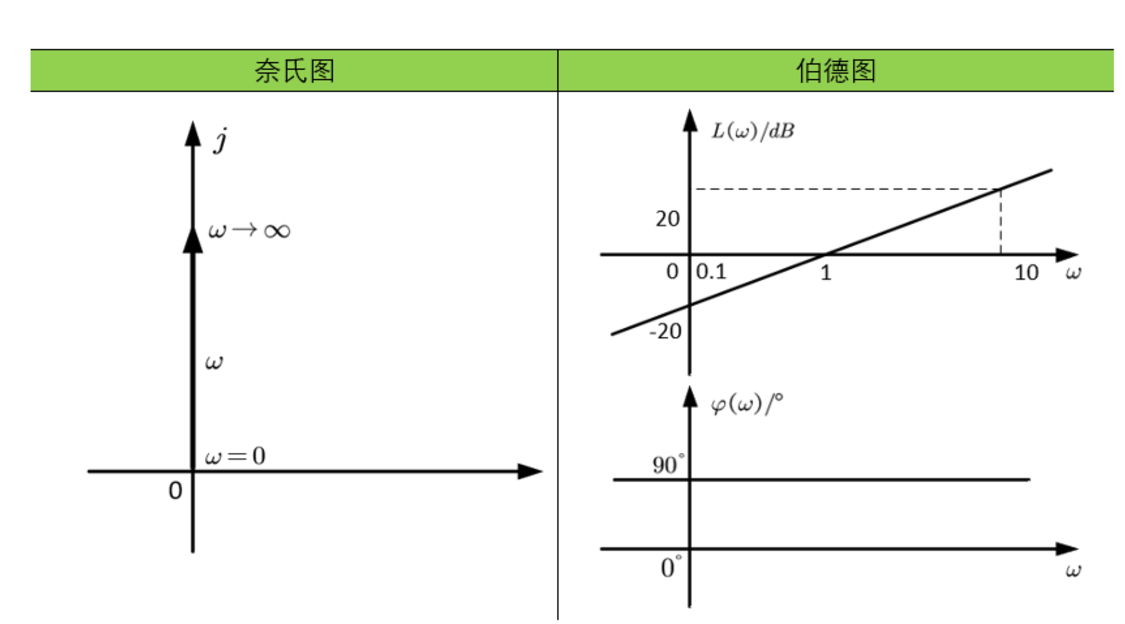
惯性环节

惯性环节的奈奎斯特图是一个半圆（数学上可证明）。在伯德图中，转折频率之后的对数幅频特性为一条$[-20]$斜率的直线（近似，实际上在转折频率处衰减了3dB）。相角变化从0°到-90°。

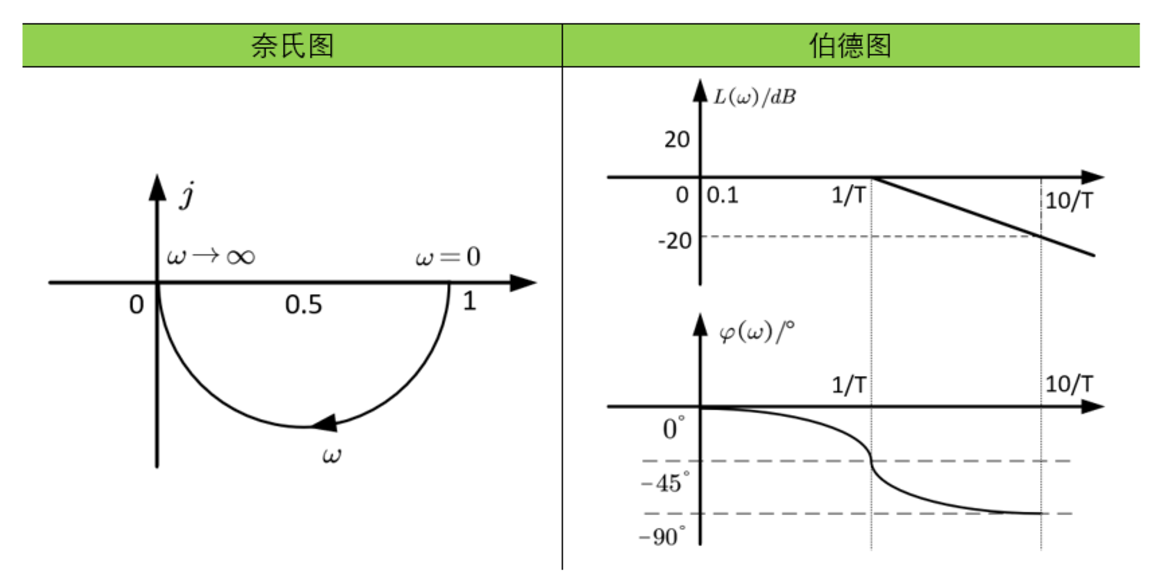
一阶微分环节

一阶微分环节的输出量取决于其输入量及一阶微分。它的奈奎斯特图相当于微分环节的图像向右平移了一个单位。它的对数频率特性与惯性环节相差一个负号，所以它们的对数频率特性关于横轴对称。

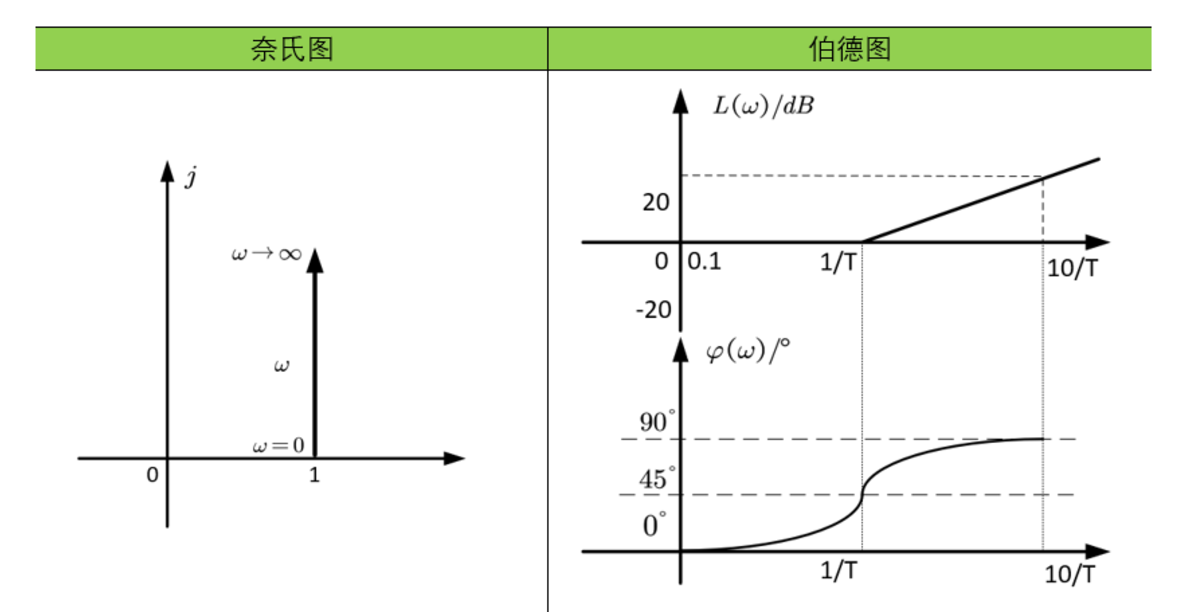
振荡环节

振荡环节的图像应该是由不同阻尼比的情况下组成的一簇曲线，它们的奈奎斯特图起于实轴1处的点，终于原点。转折频率后的模值以40dB的速度衰减。相角从0°变化到-180°。

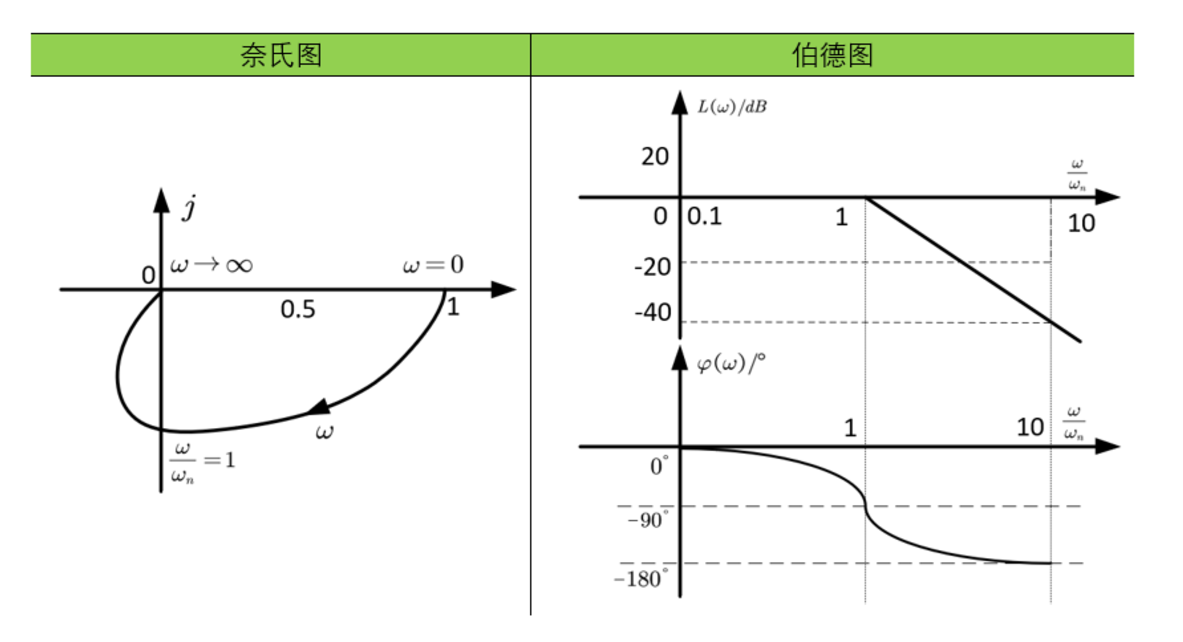
稳定性分析

控制系统在任何足够小的初始偏移下，过渡过程随着时间的推移逐渐衰减为0，则为稳定系统

对典型系统求单位脉冲响应，对得到的时域表达式进行分析得到

闭环传递函数的极点全部都在$s$平面的左半平面

代数稳定判据

根据根与系数的关系，可以得到劳斯阵列

其中有递推公式

$$b_1=\frac{a_{n-1}a_{n-2}-a_na_{n-3}}{a_{n-1}}\\ b_2=\frac{a_{n-1}a_{n-4}-a_na_{n-5}}{a_{n-1}}$$

若计算得到的第一列全为正数则稳定，否则符号变化几次就有几个根在左半平面

对于三阶多项式，可以得到

$$\begin{cases}a_i>0\\ a_1a_2>a_0a_3\end{cases}$$

奈奎斯特判据

开环传递函数$G(s)H(s)$从$-\infty j\to \infty j$包围$(-1,j0)$点的圈数

$G(s)H(s)$是实系数有理分式函数，由于对称性，一般只绘制$0\to \infty j$的图线

R=P-Z

辐角原理，参考

https://blog.csdn.net/weixin_46664967/article/details/113208585

$F(s)$绕平面原点的圈数只和$F(s)$被闭合曲线$ Γ$（取成整个右半平面） 包围$F(s)$的零点和极点的代数和有关

$$R=P−Z$$

R：R等于$ΓGH $逆时针包围F(s)平面上点 $(-1 , j0)$的圈数
P：开环传递函数在右半平面内的极点数，P是已知的
Z：闭环传递函数在右半平面内的极点数，若Z = 0 系统稳定

通过平移即可得到

步骤

作出开环系统的奈奎斯特曲线

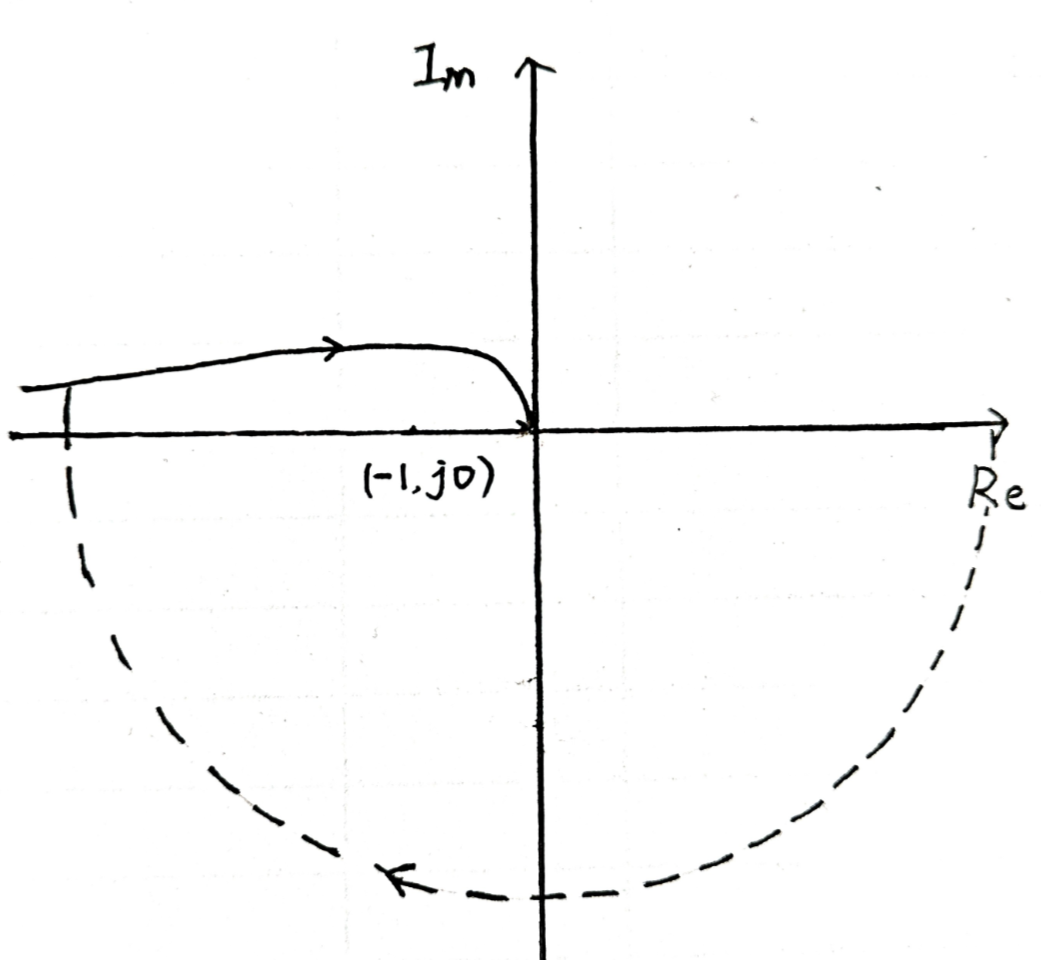
若不完整需要补圆

若有$(1/s)^v$项，则以奈奎斯特曲线的起始位置为起点，逆时针画 $v\times 90°$ 半径无穷大的圆弧，但该圆弧的方向为顺时针

$$R=2(N_+−N_−)$$

在 (-1,j0) 左侧 正穿越 的次数 (从上往下) ，N-为￥左侧 负穿越的次数 (从下往上)

R 表示开环系统 G(s)H(s) 逆时针绕点(-1,j0)的圈数，等价于1+G(s)H(s) 顺时针绕原点的圈数

N+ 表示点 (-1,j0) 左侧正穿越的次数（从上向下穿越）

N- 表示 点 (-1,j0) 左侧负穿越的次数（从下向上穿越）

只看左侧

P为开环传递函数在右半平面极点数

误差分析

理想输出和实际输出量之差为误差$e(t)$，象函数为$E(s)$，误差信号的稳态分量（静态误差），记作$e_{\text{ss}}$

输入信号和反馈信号比较后的信号$\varepsilon (t)$称为偏差

$$E(s)=\mu(s)X_i(s)-X_o(s)\\ \varepsilon(s)=X_i(s)-Y(s)$$

考虑偏差趋近于0，理想输出传递回来偏差为0，故

$$Y(s)=H(s)X_o(s)\\ \mu(s)=\frac1{H(s)}$$

故

$$\varepsilon(s)=H(s)E(s)$$

输入引起的稳态分析

对于单位反馈系统，误差等于偏差

$$X_o(s)=\frac{G(s)}{1+G(s)}X_i(s)\\ E(s)=X_i(s)-X_o(s)=\frac1{1+G(s)}X_i(s)$$

所以误差传递函数为

$$\frac{E(s)}{X_i(s)}=\frac1{1+G(s)}$$

根据终值定理

$$e_{\text{ss}}=\lim_{s\to 0}sE(s)=\lim_{s\to 0} s\frac1{1+G(s)}X_i(s)$$

对于非单位反馈系统

$$\varepsilon(s)=\frac1{1+G(s)H(s)}X_i(s)$$

稳态偏差为

$$\varepsilon_{\text{ss}}=\lim_{s\to 0}s\frac1{1+G(s)H(s)}X_i(s)\\ e_{\text{ss}}=\lim_{s\to 0}s\frac1{H(s)}\frac1{1+G(s)H(s)}X_i(s)$$

一般$H(s)$为常数，故

$$e_{\text{ss}}=\frac{\varepsilon_{\text{ss}}}{H}$$

静态误差系数

对于单位阶跃响应

$$X_i(s)=\frac1s$$

稳态偏差为

$$\varepsilon_{\text{ss}}=\lim_{s\to 0}s\frac1{1+G(s)H(s)}\frac1s=\lim_{s\to 0}\frac1{1+G(s)H(s)}\\$$

可以定义静态误差系数为

$$K_p=\lim_{s\to0}G(s)H(s)=G(0)H(0)\\ \varepsilon_{\text{ss}}=\frac1{1+K_p}$$

对于$0$型而言

$$K_p=K\\ \varepsilon_{\text{ss}}=\frac1{1+K}$$

对于高于$\rm I$型的系统，分母$s\to 0$

$$K_p= \infty,\;\; \varepsilon_{\text{ss}}=0$$

静态速度加速度误差系数

对于单位斜坡输入

$$\varepsilon_{\text{ss}}=\lim_{s\to 0}s\frac1{1+G(s)H(s)}\frac1{s^2}=\lim_{s\to 0}\frac1{sG(s)H(s)} \\K_v=\lim_{s\to0}sG(s)H(s)\\ \varepsilon_{\text{ss}}=\frac1{K_v}$$

同理对于单位加速度输入，也有静态加速度系数

$$K_a=\lim_{s\to0}s^2G(s)H(s)\\ \varepsilon_{\text{ss}}=\frac1{K_a}$$

总结如下表

系统类别	单位阶跃	等速输入	等加速输入
0型系统	$\frac1{1+K}$	$\infty$	$\infty$
I型系统	$0$	$\frac1K$	$\infty$
II型系统	$0$	$0$	$\frac1K$

干扰引起的误差

忽略输入，只计算干扰

$$\varepsilon(s)=\frac{-G_2(s)H(s)}{1+G_2(s)G_1(s)H(s)}N(s)$$

之后可以用叠加原理计算总误差