逆运动学

$\rm DOF=3\quad(\theta_1,\theta_2,\theta_3)$

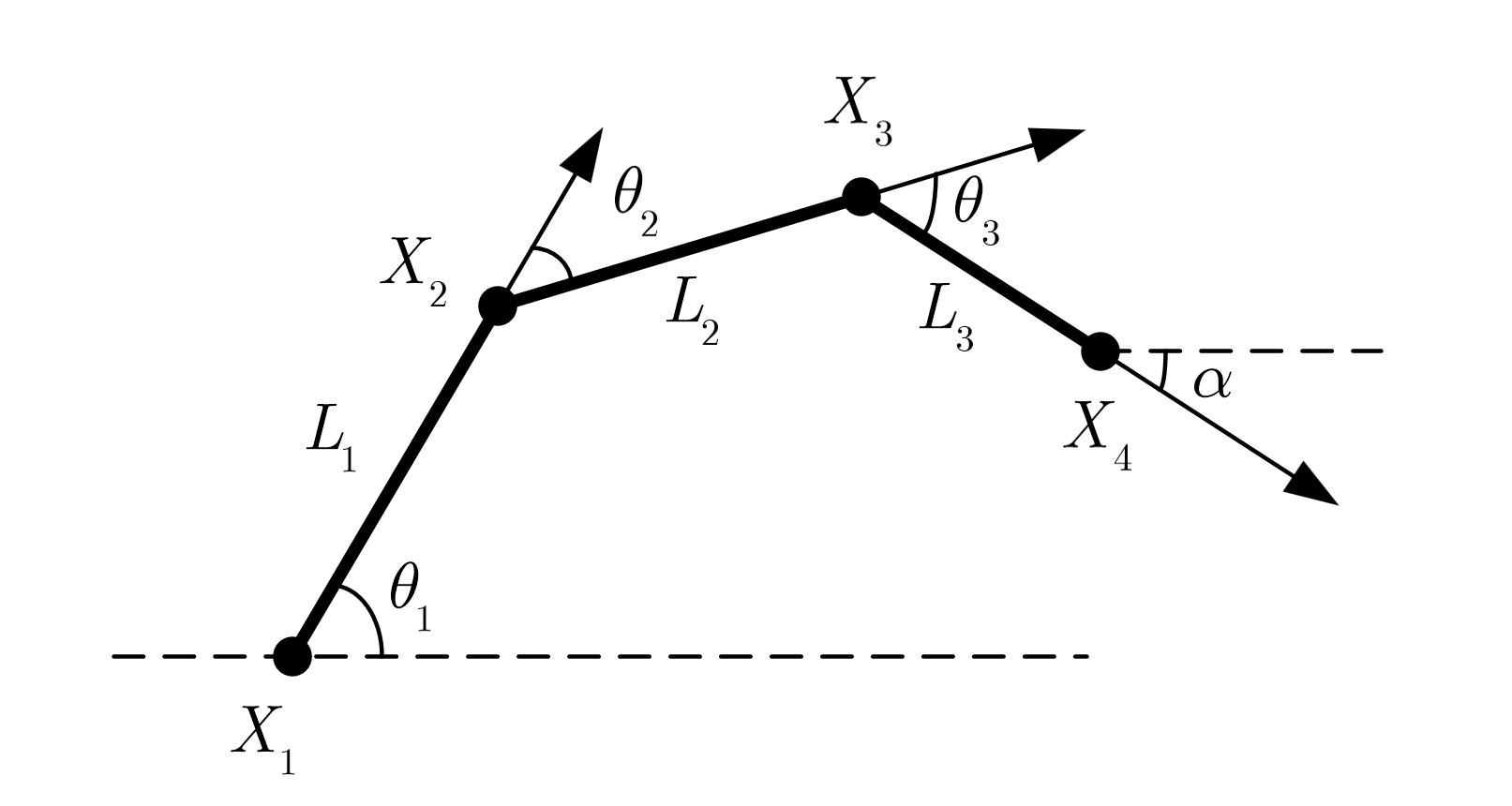
所以可以控制三个关节的转角来使得机械臂末端$X_4$运动到

$(x,y,\alpha)$

求解过程

$\begin{cases}X_{3x}=X_{4x}-L_3\cos\alpha\\X_{3y}=X_{4y}-L_3\sin\alpha\end{cases}$

利用余弦定理求解$\theta_1,\theta_2$

$\theta_1=\beta\pm\gamma\\ \tan\beta=\frac{X_{3y}}{X_{3x}}$

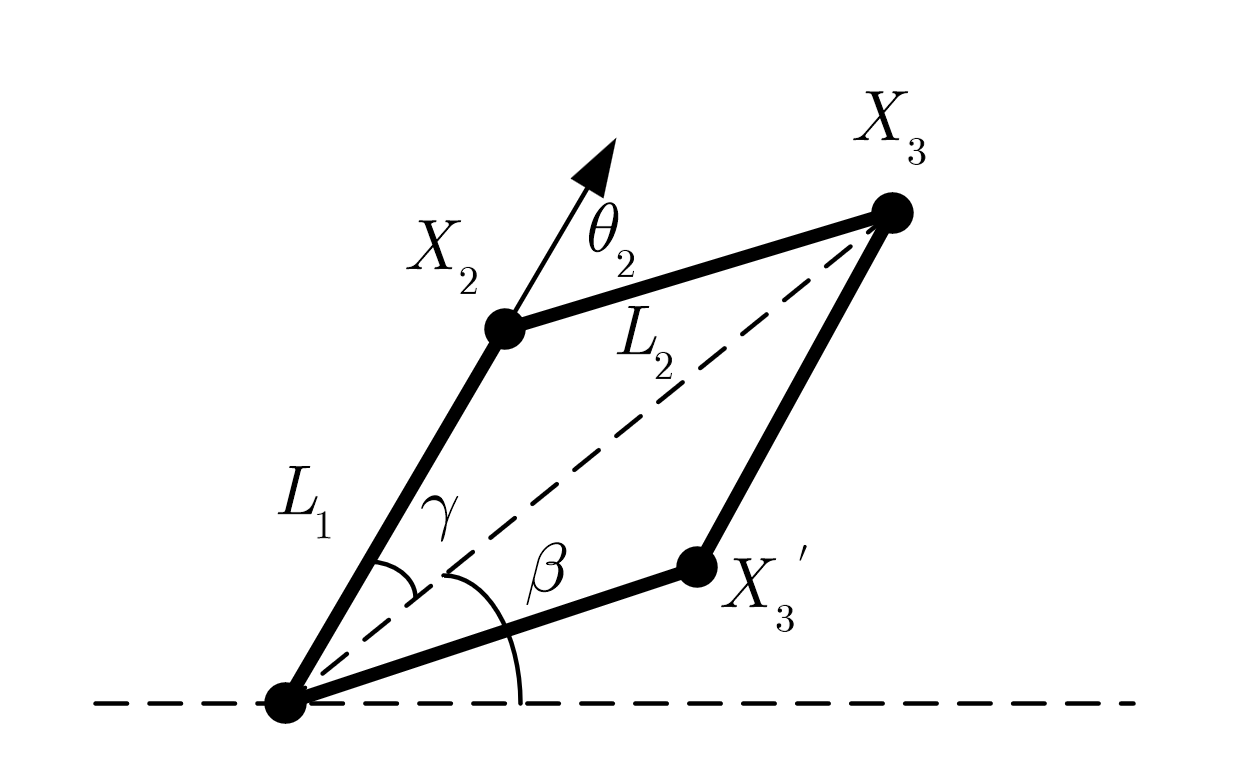
在三角形内使用余弦定理

$\cos\theta_2=\frac{(X_{3y}^2+X_{3x}^2)-L_1^2-L_2^2}{2L_1L_2}\\ \cos\gamma=\frac{(X_{3y}^2+X_{3x}^2)+L_1^2-L_2^2}{2L_1\sqrt{X_{3y}^2+X_{3x}^2}}$

所以

$\theta_3=\alpha-\theta_2-\theta_2$

由于自由度受限，故空间内机械臂规划只考虑

$\alpha=90^\circ$，即垂直抓取的情况，考虑俯视图

砖块处在相对$X_0$，$(x,y)$的位置，位姿为$\theta$

云台转角为$\theta_0$，夹爪的转角为$\theta_4$

$\sqrt{x^2+y^2}=X_{4x}\\ \tan\theta_0=\frac {x}{y}\\ \theta=\theta_0+\theta_4$

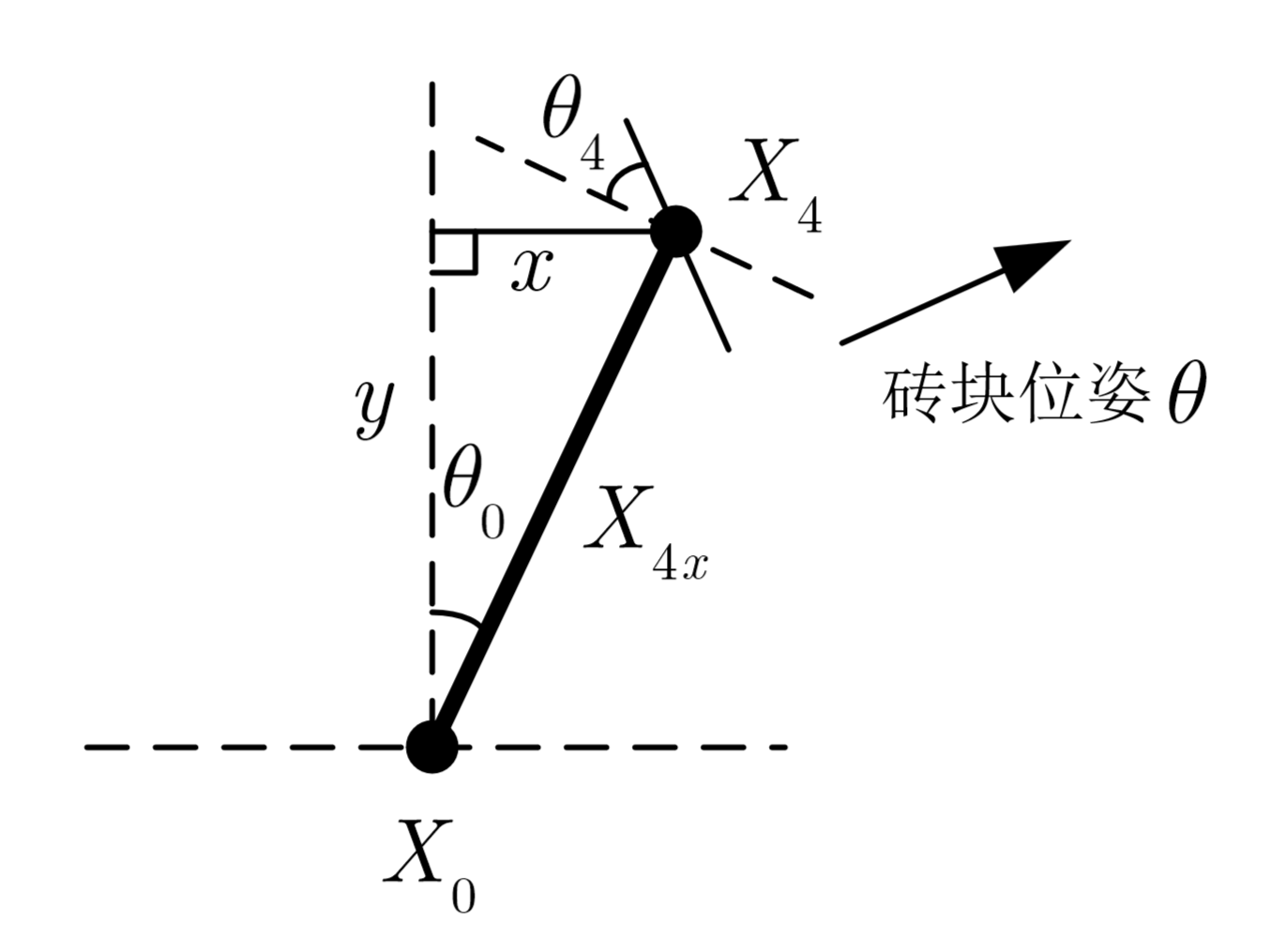
通过这些方程可以求解出$\theta_0,\theta_1,\theta_2,\theta_3,\theta_4$

再通过$\theta_5$控制夹爪的张开与夹紧就可实现完整的抓取

轨迹生成

贝塞尔曲线具有良好的空间连续性,采用空间贝塞尔曲线的路径,不仅可有效增加空间曲线的平滑性并可通过更改控制点修改局部速度及加速度值,同时可通过控制点修改曲线形状,并且具有较高的计算效率。

Bernstein基函数

$B_i^{(n)}(t)={n\choose i}t^i(1-t)^{n-i}$

Bezier曲线的表达式

$f(t)=\sum_{i=1}^nb_i(t)\boldsymbol{p}_i$

在计算机图形学常用De Casteljau来对贝塞尔曲线进行求值

算法利用如下递归表达式来实现

$\boldsymbol{b}_i^{(r)}=(1-t)\boldsymbol{b}_i^{(r-1)}+t\boldsymbol{b}_{i+1}^{(r-1)}$

轨迹设计

由于我们需要将砖块一块一块砌筑，并且需要保证尽可能垂直向下放置砖块，从而能利用榫卯结构让两砖块之间能够贴合且不发生碰撞，所以为简单起见采用三个点作为控制顶点，分别是机械臂末端起点，终点，和终点正上方$d$处的控制点，利用贝塞尔曲线的端点性质，保证接近终点时速度一定垂直向下。

由于对于轨迹上的任意一点$(x,y,z,\alpha)$，我们需要确定$\alpha$的取值使得和机械臂的四个关节角度$(\theta_0,\theta_1,\theta_2,\theta_3)$一一对应从而求解，我们采用一种启发式的方式来设定$\alpha_t$，设当前进度为$t,t\in[0,1]$，则

$\alpha_t=t\alpha_e+(1-t)\alpha_0$

再利用搜索的方式找到离$\alpha_t$最近且使得逆运动学有解的$\alpha$，从而求解四个关节角度。

由于当关节角度$\theta=0$时，存在奇异点，末端执行器的一点微小变化会导致机械臂角度剧烈变化，产生震荡，所以在保证终点处不会存在角度为$0$后，我们可以对求解出角度小于某个设定阈值的部分不采用这段轨迹，并对关节角度利用线性插值的方式来生成新轨迹，使得轨迹更加稳定。

但由于局部突然用线性插值来替代，导致轨迹不够平滑，衔接处加速度过大，所以采用Savitzky-Golay滤波对新轨迹进行平滑，从而得到更加自然，加速度更小的轨迹

we need to lay bricks one by one and ensure that they are placed as vertically as possible to utilize the mortise and tenon structure to ensure that the bricks can fit together without colliding, three points are chosen as control vertices for simplicity. These points are the starting point of the robotic arm end effector, the endpoint, and a control point $d$ directly above the endpoint. Using the endpoint property of the Bézier curve, it ensures that the speed is strictly vertical as it approaches the endpoint.

For any point $(x, y, z, \alpha)$ on the trajectory, we need to determine the value of $\alpha$ so that it corresponds to the four joint angles $(\theta_0, \theta_1, \theta_2, \theta_3)$ of the robotic arm. We use a heuristic method to set $\alpha_t$. Let the current progress be $t, t \in [0, 1]$, then

$\alpha_t=t\alpha_e+(1-t)\alpha_0$

Then, by searching for the closest $\alpha$ to $\alpha_t$ that allows for solvable inverse kinematics, the four joint angles can be solved.

Since there are singular points when the joint angle $\theta = 0$, a slight change in the end effector will cause drastic changes in the angles of the robotic arm, resulting in oscillations. Therefore, after ensuring that there are no angles equal to $0$ at the endpoint, we can discard the portion of the trajectory where the angles are less than a certain threshold and use linear interpolation for the joint angles to generate a new trajectory, making the trajectory more stable.

However, abruptly replacing parts of the trajectory with linear interpolation makes it less smooth, with excessive acceleration at the junctions. Hence, we use Savitzky-Golay filtering to smooth the new trajectory, resulting in a more natural trajectory with lower acceleration.