基本概念
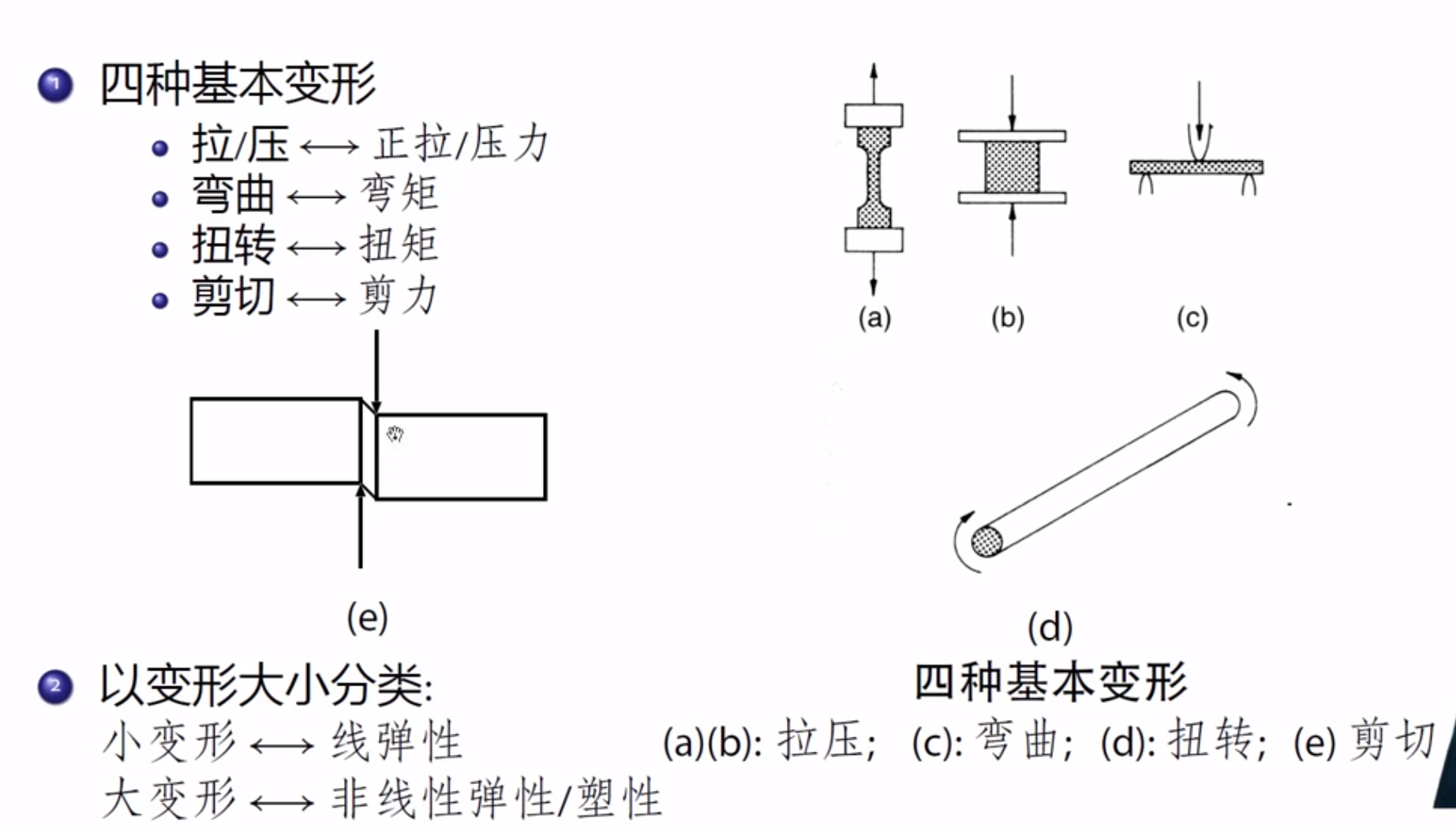
应力应变
胡克定律
关系,泊松比$\nu$
只在一个方向有线应变有横向变形效应
广义胡克定律
特别的,对于平面应力状态,有
许用应力
衡量材料力学性能的指标
剪切
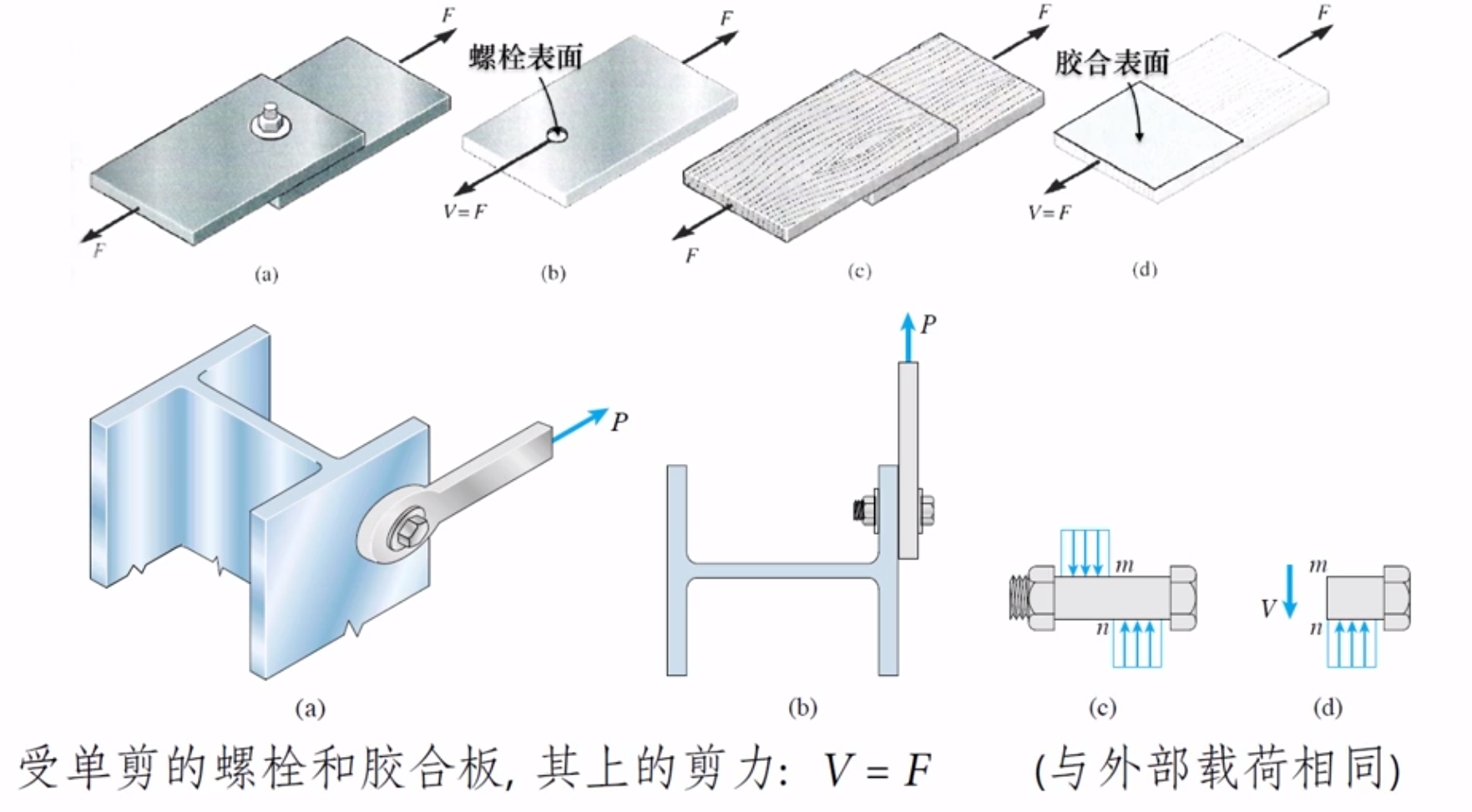
单剪
双剪
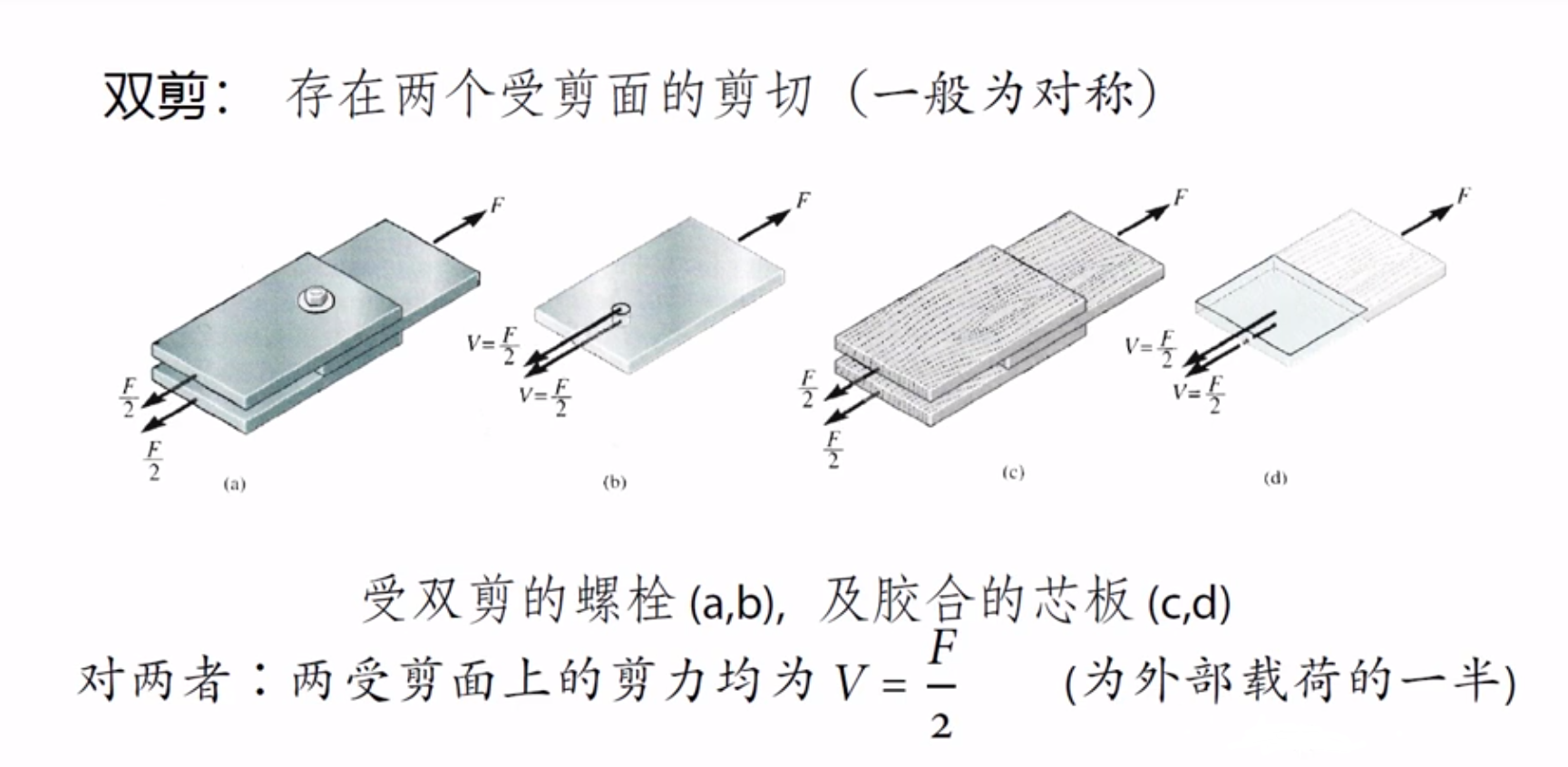
同时存在挤压
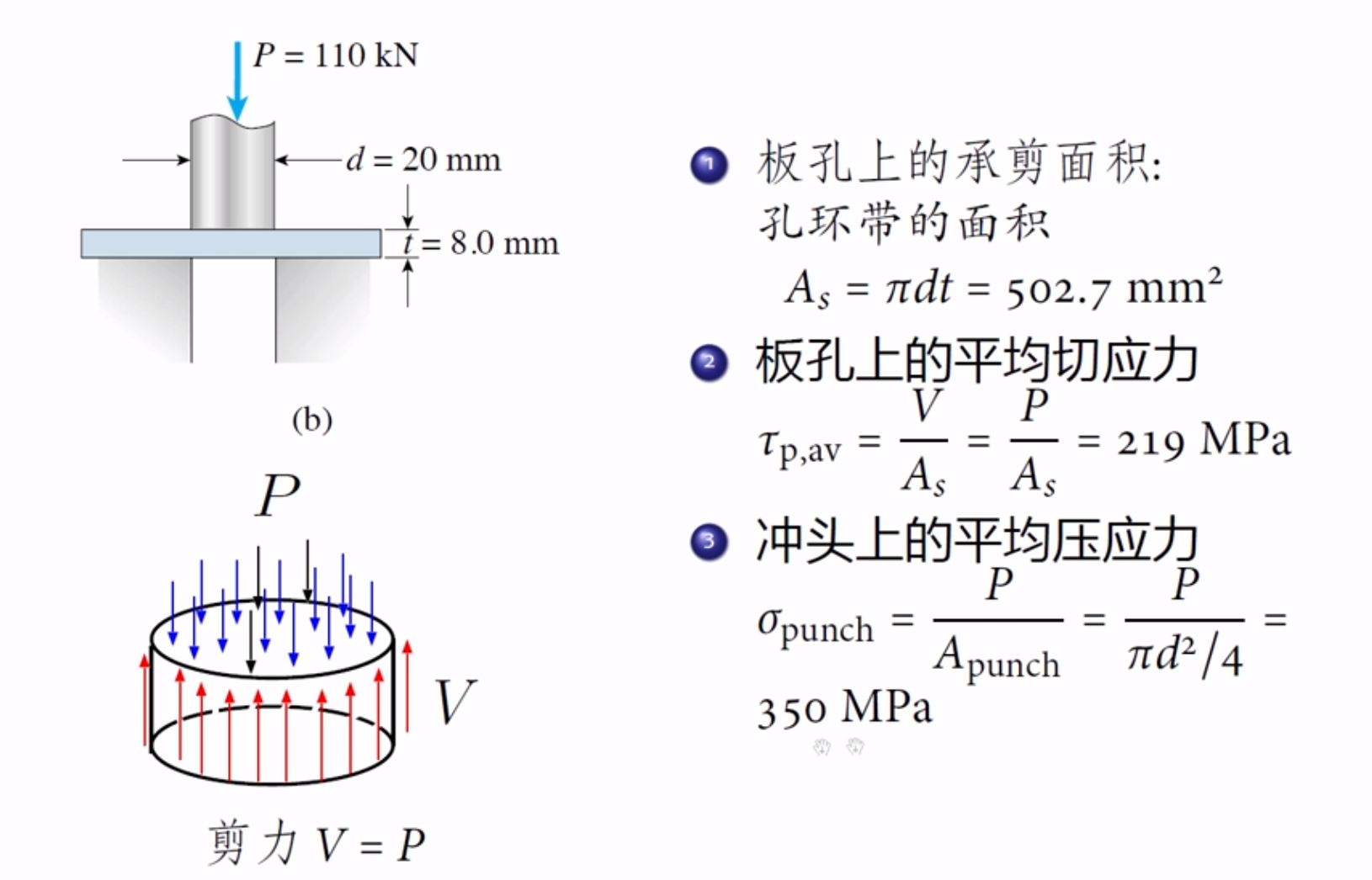
计算切和压只需要判断力和面积
剪切:剪力对应接触面积
挤压:压力对应正交面积
扭转
截面上的扭转
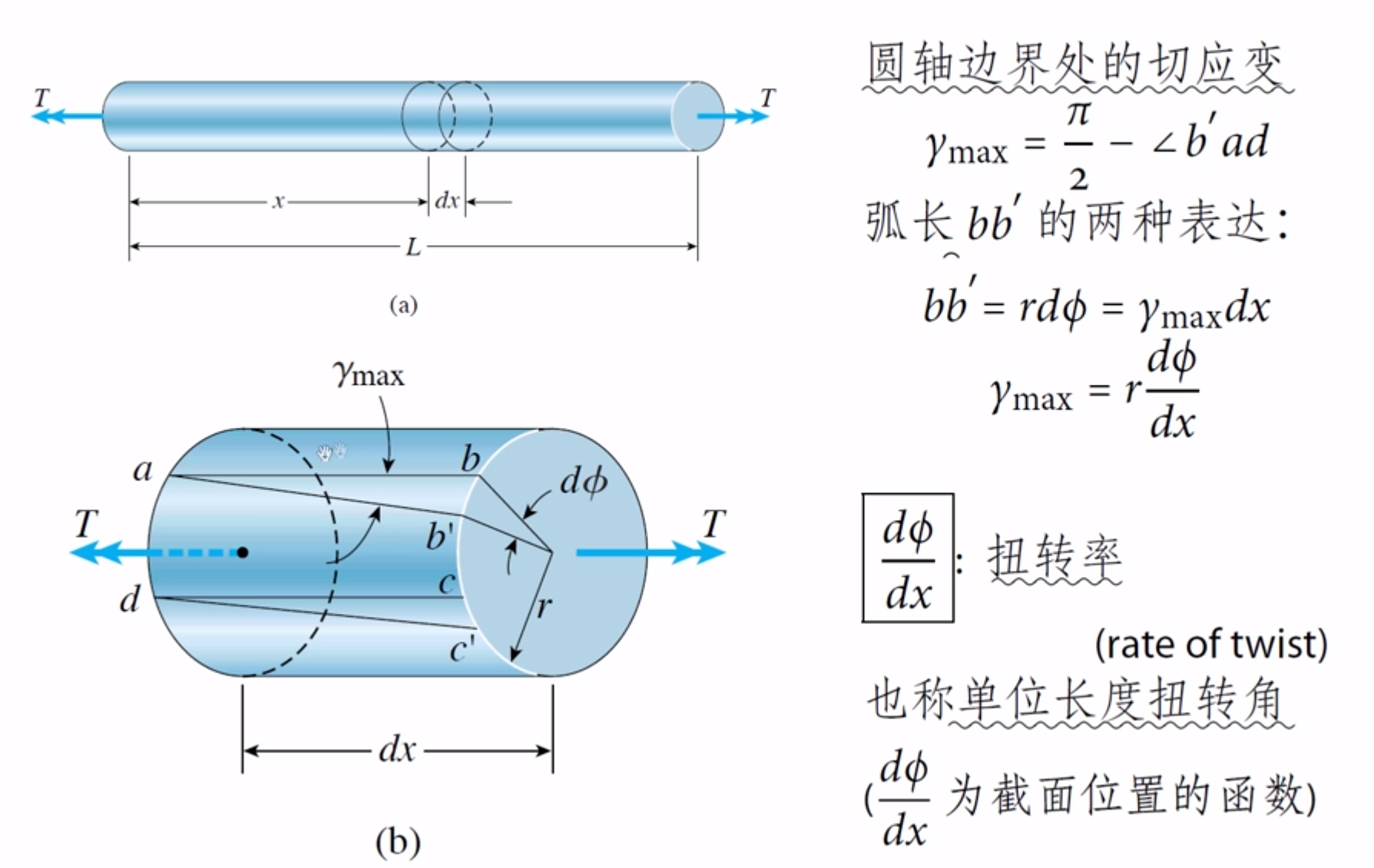
切应力
其中$I_p$为截面的极惯性矩
对于圆
空心
对于半径处(表面),截面系数为
单位长度扭转角
单位为弧度,要转角度,则
安全条件
强度条件
刚度条件
计算时画出扭矩图
弯曲
简支梁
两端分别为固定铰支座和活动铰支座
悬臂梁
一端为固定端一端为自由端
外伸梁
至少有一个铰支座不在梁端部
剪力弯矩
利用力的平衡可以得到剪力和弯矩
同时注意剪力以顺时针为正
弯矩以凹为正,同时弯矩图画在拉的那一侧(朝下)
需要标明正负
弯曲正应力
中性层为基准
正应力随高度呈线性变化,正比弯矩,反比于形心主惯性矩,两侧正应力一拉一压,总是同时存在
惯性矩计算
对矩形截面
空心圆形
同时利用对称性来计算
四矩式
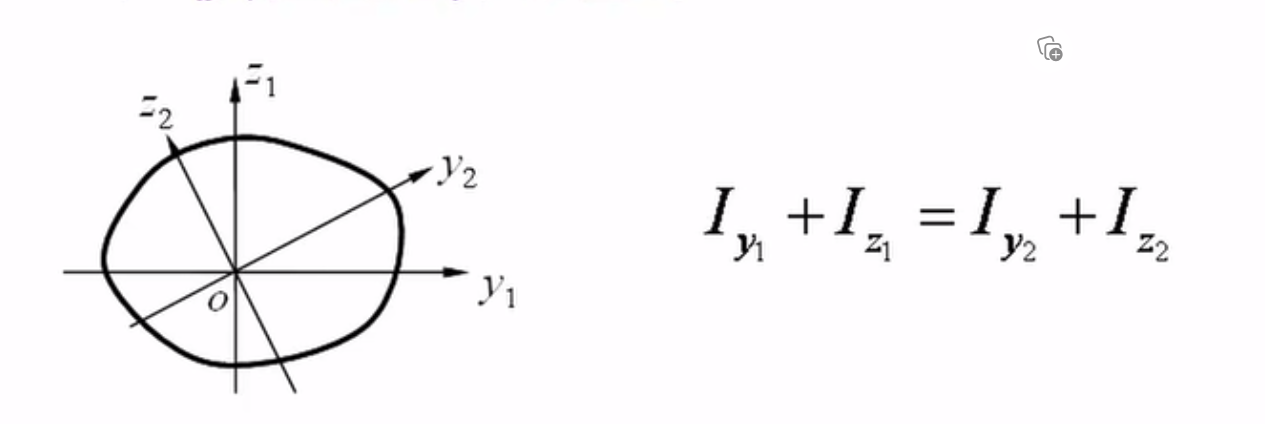
切应力
其中$S_z^*(y)$为静矩
利用形心来计算,$b$为厚度
掌握计算校核设计截面的方法,分析危险截面
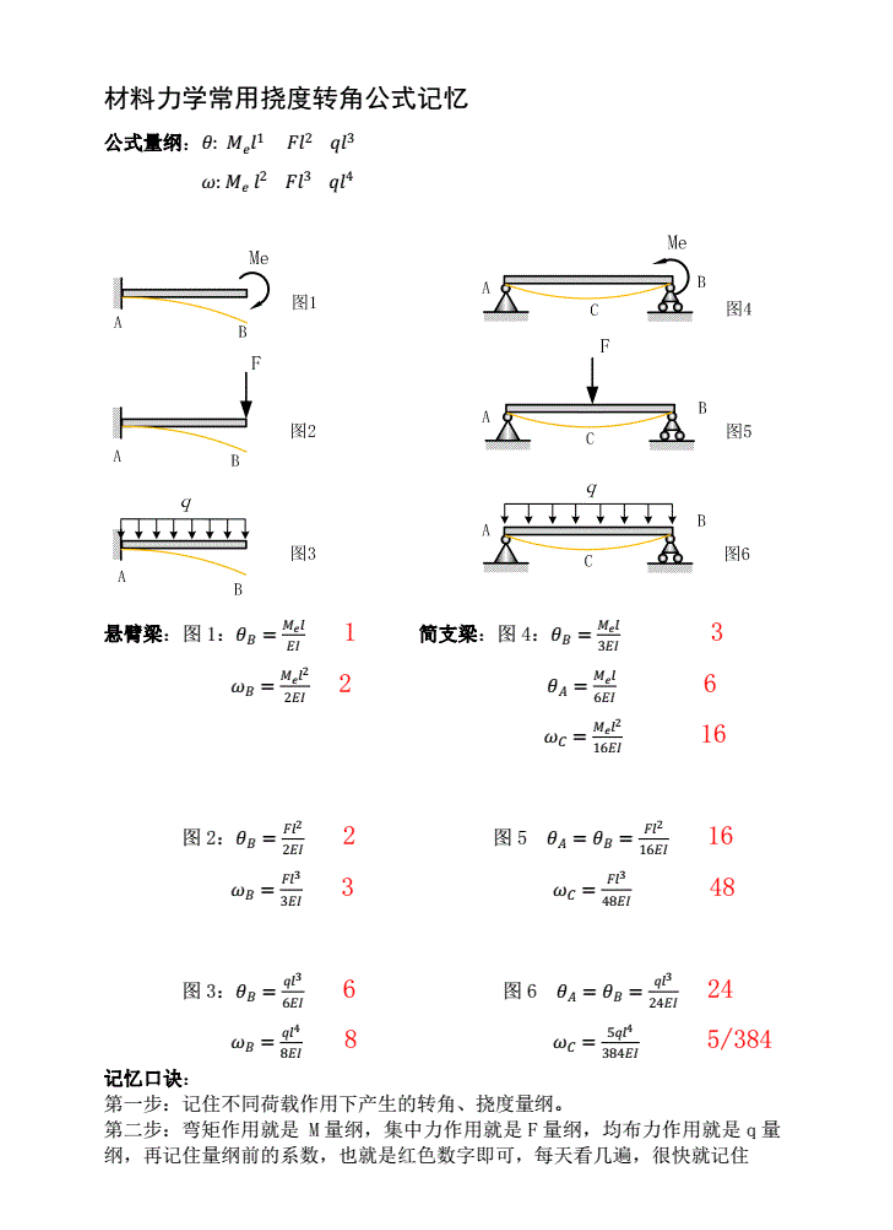
梁的变形
挠度$y$,为相对的位置变化
则利用微分方程得到
进行积分,带入边界条件尽可能早的确定常数
如固定端$\theta,y=0$,铰链左右转角相等 等等
利用叠加法首先将所有的载荷等效到一段
用相差一个刚体位移的方法进行计算
应力状态分析
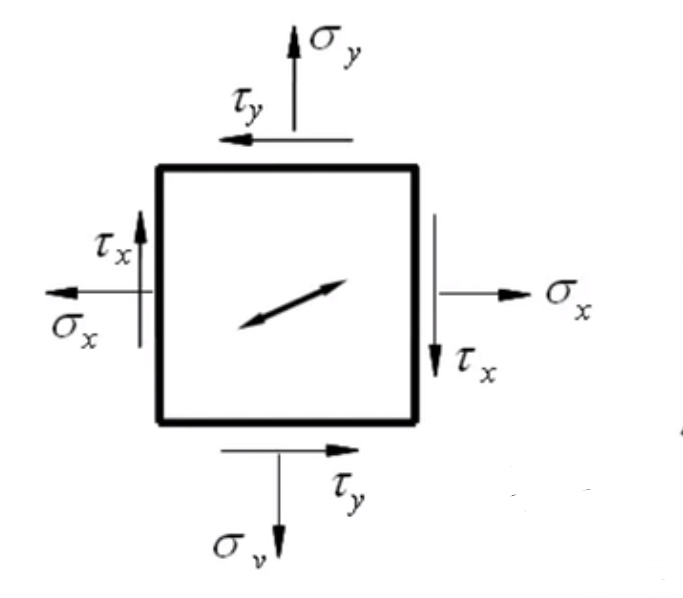
正应力以拉为正,压为负
切应力以外法线顺时针旋转
对任意角度,有
则有
相互垂直截面上的正应力之和为常数
主平面
可画出应力圆求解
对于切应力极值,与主平面呈45度角,此时正应力为
对于空间应力,$\sigma_z\ne0,\tau_z=0$
所以$z$已经是主平面,求处另外两个主应力,画在一起
为三向应力圆
强度理论
主应力按照从大到小的顺序排列后
四个强度理论
还有莫尔强度理论
特别的,对于单向
更特别的
切应力主要为扭矩产生,正应力主要为弯矩产生
组合变形
分别在$x,y$方向上画弯矩图
计算最大应力时,分解后叠加
注意$M_y$为$F_z$产生
同理挠度也叠加
偏心压缩
将心的力$F_2$等效成
转换成一个正应力和弯矩
压杆稳定性
对于不同支承条件,长度系数不同
如果两端铰支,都可以转动(角度任意变化)
或者两端固定另一端可以横向移动
若一端自由另一端固定
两端固定
一端固定,一端铰支
所以临界压力
引入柔度的概念
其中$i=\sqrt{\frac {I_z}{A}}$,截面对失稳弯曲时的中性轴的惯性半径
所以临界应力公式为
则柔度需要满足
对于铸铁$\rm Q235$
对于中长杆,可以使用经验公式
或者