二重积分

$\lambda=\max\{\Delta A_k\}\\ \iint_Df(x,y)\text d\sigma=\lim_{\lambda\to0}\sum _if(\xi_i,\eta_i)\Delta A_i$

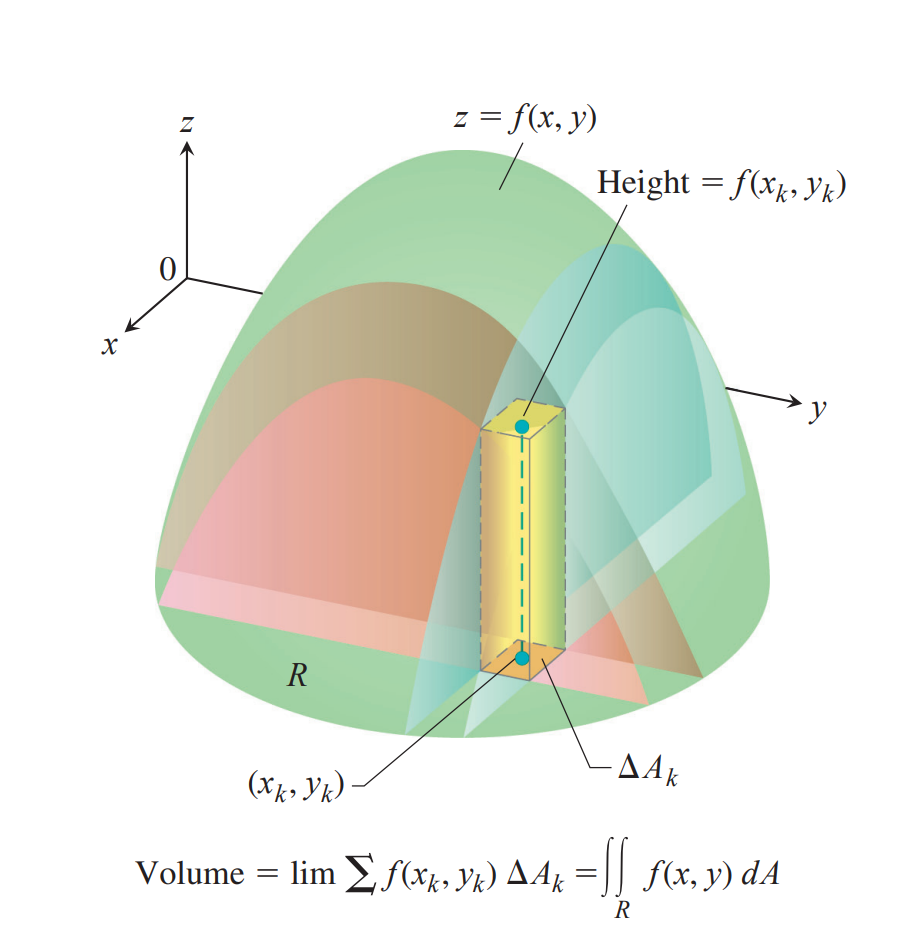
其中$f(x,y)$称为被积函数，$f(x,y)\text d\sigma$称为被积表达式，积分区域为$D$，$\text d\sigma$为面积元素，$\displaystyle \sum _if(\xi_i,\eta_i)\Delta A_i$称为积分和

性质

可加性

$\iint_D=\iint_{D_1}+\iint_{D_2}$

线性

$a\iint_D\text d \sigma=\iint_Da\text d \sigma\\ \iint_D[\alpha f+\beta g]\text d \sigma=\alpha\iint_Df \text d \sigma+\beta\iint_Dg\text d \sigma\\$

绝对值不等式

$\left|\iint_Df\text d\sigma\right|\le\iint_D|f|\text d\sigma$

估值

$m\sigma\le\iint_Df(x,y)\text d\sigma\le M\sigma$

中值定理

$\iint_Df(x,y)\text d\sigma=f(\xi,\eta)\sigma$

平均值

$\overline{f}=\frac{\displaystyle \iint_Df(x,y)\text d\sigma}{\sigma}$

对称性

如果$D$关于$x$轴对称，被分为$D_1$和$D_2$

$f(x,y)=-f(x,-y)\Rightarrow\iint_Df=0\\ f(x,y)=f(x,-y)\Rightarrow\iint_Df=2\iint_{D_1}f$

若$D$关于$y=x$对称

$\iint_Df(x,y)=\iint_{D}f(y,x)$

若$D_1$和$D_2$关于$y=x$对称

$\iint_{D_1}f(x,y)=\iint_{D_2}f(y,x)$

计算法

直角坐标

$\iint_Df(x,y)\text d\sigma=\iint_Df(x,y)\text dx\text dy$

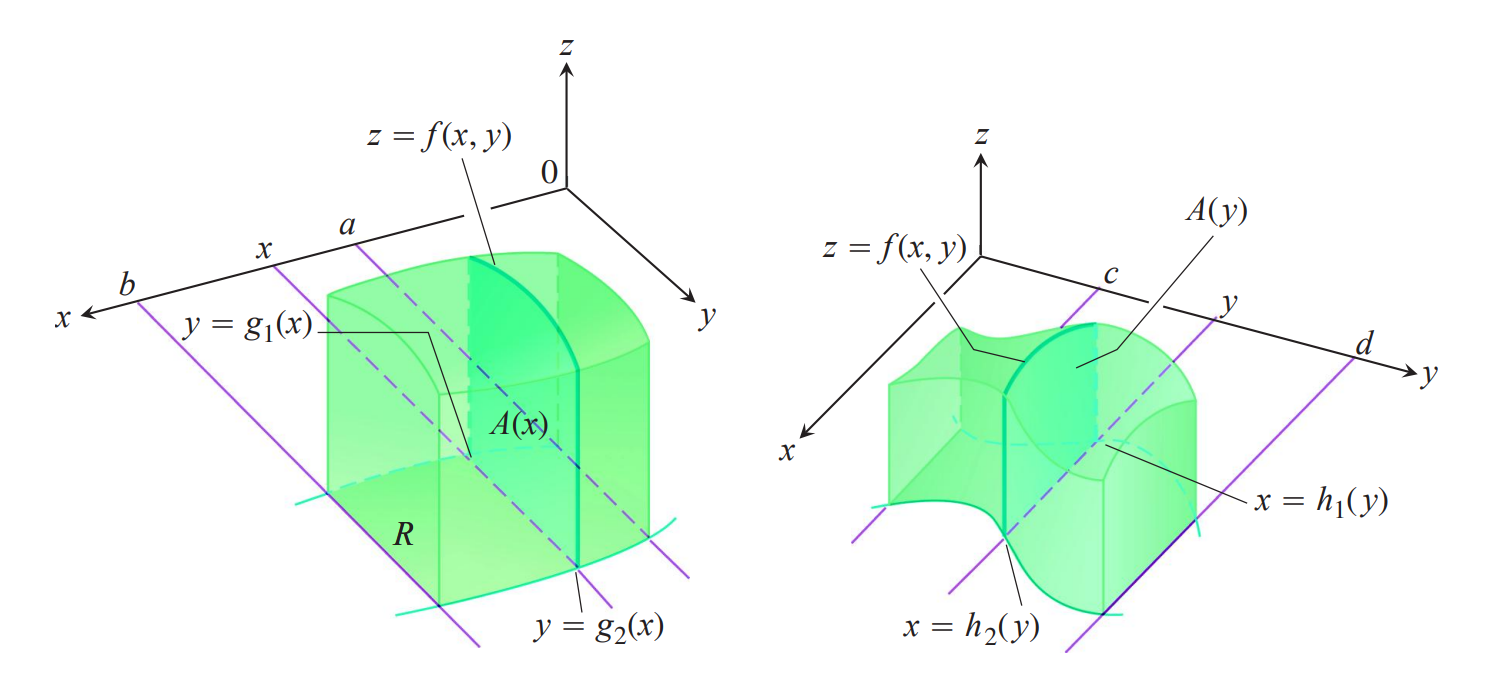
先在一条线上作定积分，再对线作定积分

$x:\quad I=\int_a^b\text dx\int_{g_1(x)}^{g_2(x)}f(x,y)\text dy\\ x:\quad I=\int_c^d\text dy\int_{h_1(y)}^{h_2(y)}f(x,y)\text dx$

极坐标

$I=\int_{\theta_1}^{\theta_2}\text d\theta\int_{\rho_1(\theta)}^{\rho_2(\theta)}f(\rho\cos\theta,\rho \sin \theta)\rho\text d\rho$

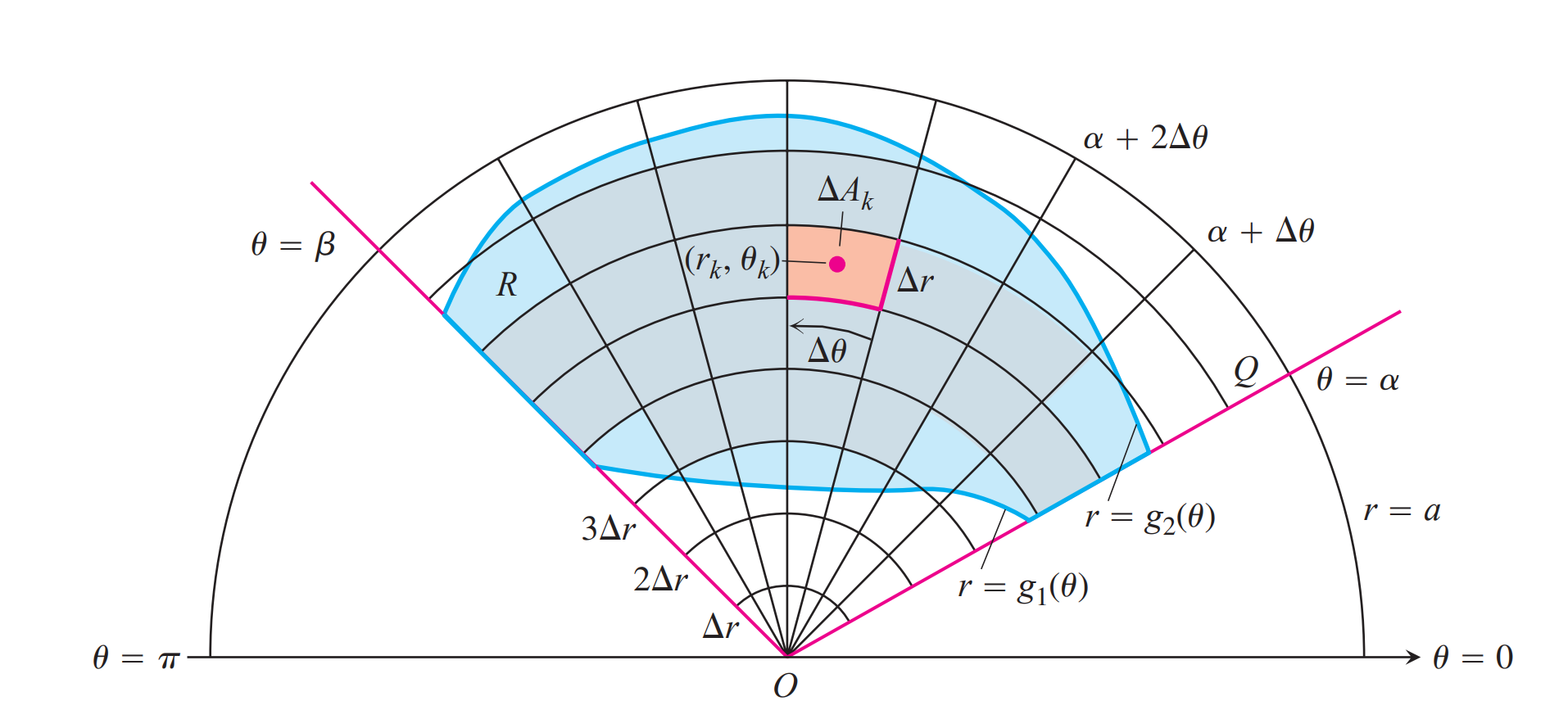
注意积分上下限，如双扭线$\rho=\sqrt{4\cos 2\theta}$

平移变换

$\iint_Df(x,y)\text dx \text dy=\iint_{D'}f(u+x_0,v+y_0)\text du\text dv$

换元积分

满足条件

有雅可比$x(u,v),y(u,v)$在D上一阶偏导连续

$J(u,v)=\frac{\partial(x,y)}{\partial(u,v)}\ne0$

且$D’\to D$ 的变换为一一映射，则有

$I=\iint_{D'}f[x(u,v),y(u,v)]|J(u,v)|\text du\text dv\\ |J(u,v)|=\frac1{|J(x,y)|}$

画出还原后的区域即可

三重积分

$\lambda=\max\{\Delta V_k\}\\ \iiint_{\Omega}f(x,y,z)\text dv=\lim_{\lambda\to0}\sum _if(\xi_i,\eta_i,\zeta _i)\Delta V_i$

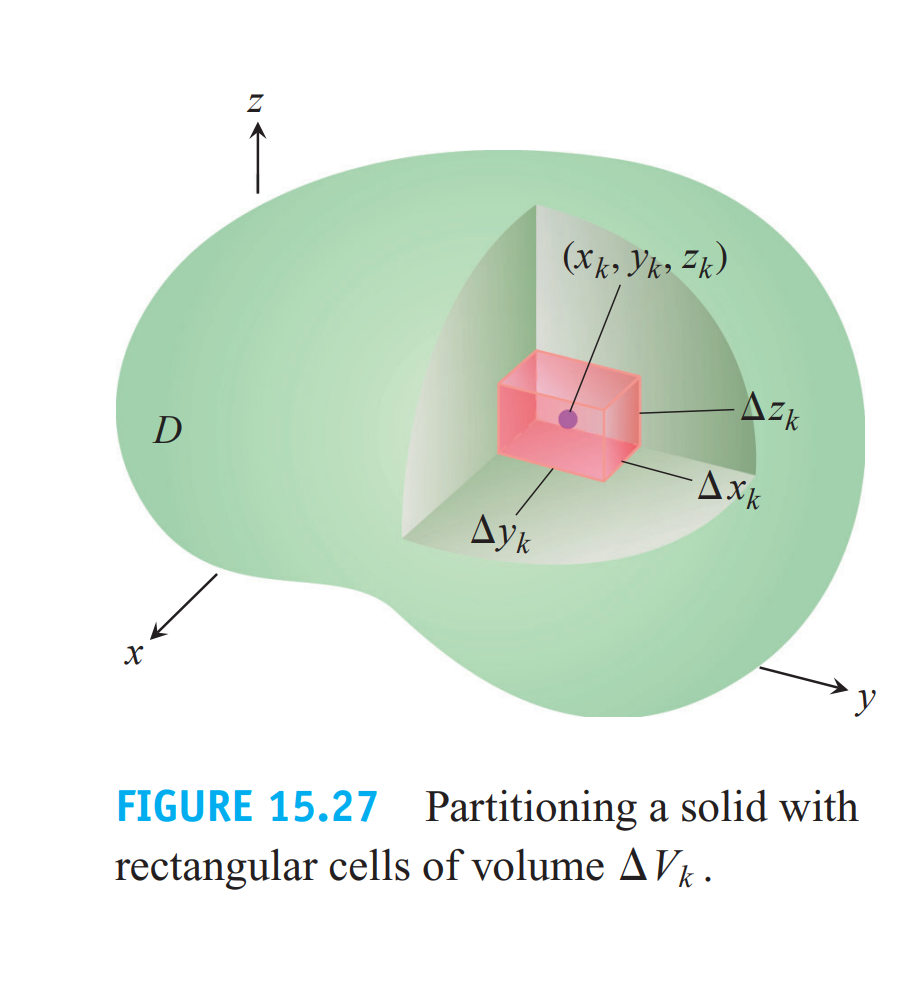
计算法

三次积分

$I=\int_a^b\text dx\int_{y_1(x)}^{y_2(x)}\text dy\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)\text dz$

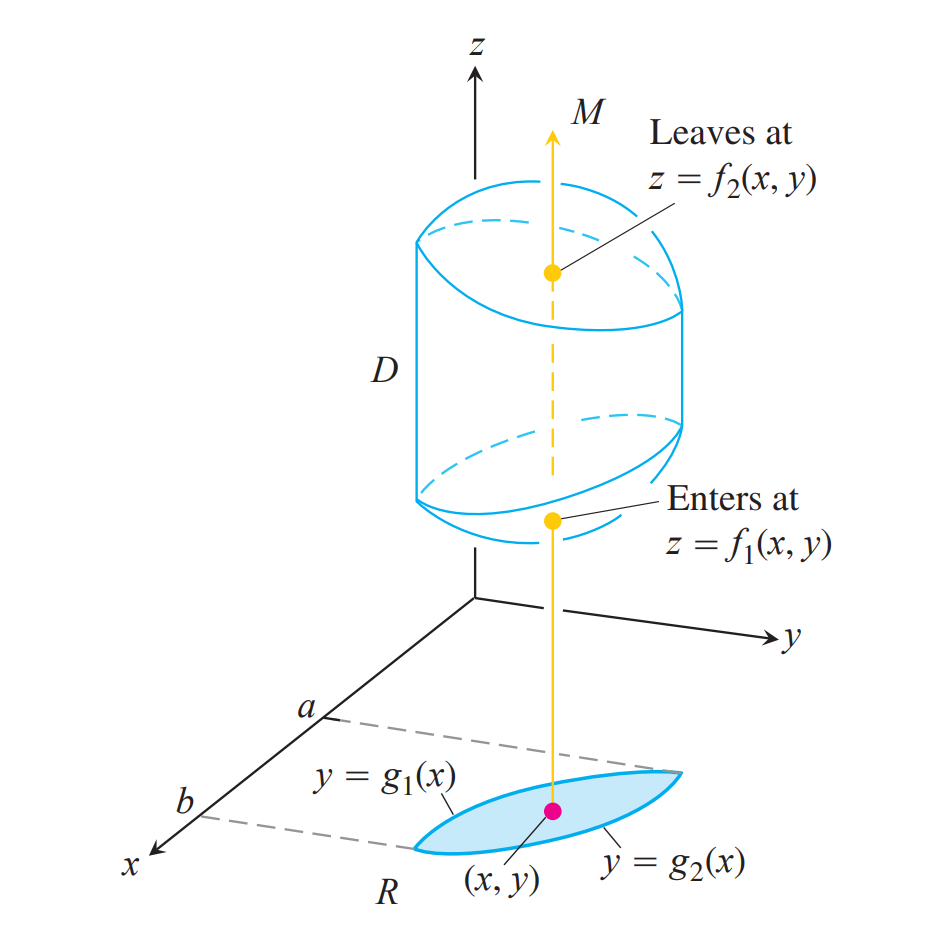
先找到投影区域再对$z$积分从而化为二次积分，积分可换序

也可先计算二重积分(投影法)

$I=\int_{c_1}^{c_2}\text dz\iint_{D_z}f(x,y,z)\text dy\text dz$

柱面坐标

对二重积分使用极坐标得到

$I=\int_{\theta_1}^{\theta_2}\text d\theta\int_{\rho_1(\theta)}^{\rho_2(\theta)}\rho\text d\rho\int_{z_1(\theta,\rho)}^{z_2(\theta,\rho)}f(\rho\cos\theta,\rho \sin \theta,z)\text dz$

球坐标

$\begin{cases}x=r\sin\varphi\cos\theta\\ y=r\sin\varphi\sin\theta\\ z=r\cos\varphi\end{cases}$

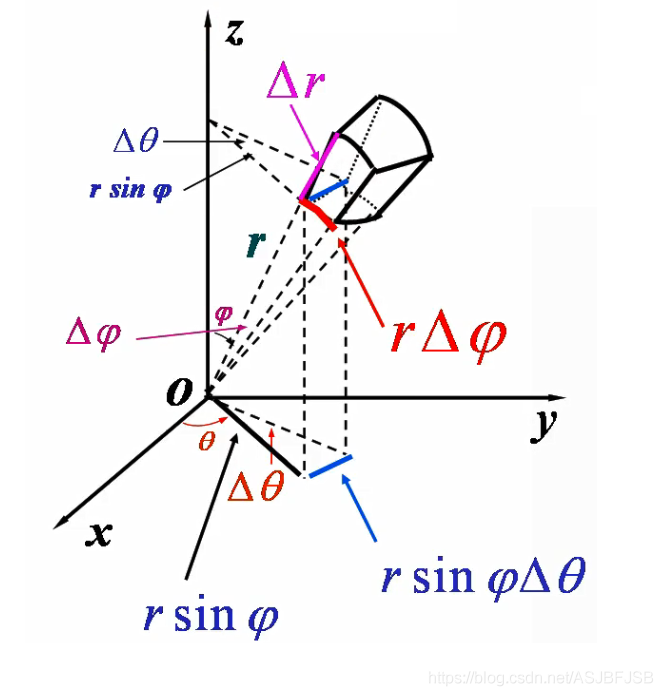
20200905200443461

$I=\int_{\theta_1}^{\theta_2}\text d\theta\int_{\varphi_1(\theta)}^{\varphi_2(\theta)}\sin\varphi\text d\varphi\int_{r_1(\theta,\varphi)}^{r_2(\theta,\varphi)}f(x,y,z)r^2\text dr$

一定要画出积分区域

应用

曲面面积

$A=\iint_D\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2}\text dx\text dy$ $E=x_{u}^{2}+y_{u}^{2}+z_{u}^{2} \\ F=x_{u} \cdot x_{v}+y_{u} \cdot y_{v}+z_{u} \cdot z_{v} \\ G=x_{v}^{2}+y_{v}^{2}+z_{v}^{2} \\ A=\iint_{D} \sqrt{E G-F^{2}} \mathrm{~d} u \mathrm{d} v$

质心

$x_C=\frac{\displaystyle \iiint_{\Omega} x \text dv}{V}$

转动惯量

$I_L=\displaystyle \iiint_{\Omega} r^2(x,y)\rho(x,y) \text dv\\ I_z=\displaystyle \iiint_{\Omega} (x^2+y^2)\rho(x,y) \text dv$

曲线积分

第一类

$\lambda=\max\{\Delta s_k\}\\ \int_Lf(x,y,z)\text ds=\lim_{\lambda\to0}\sum _if(\xi_i,\eta_i,\zeta_i)\Delta s_i$

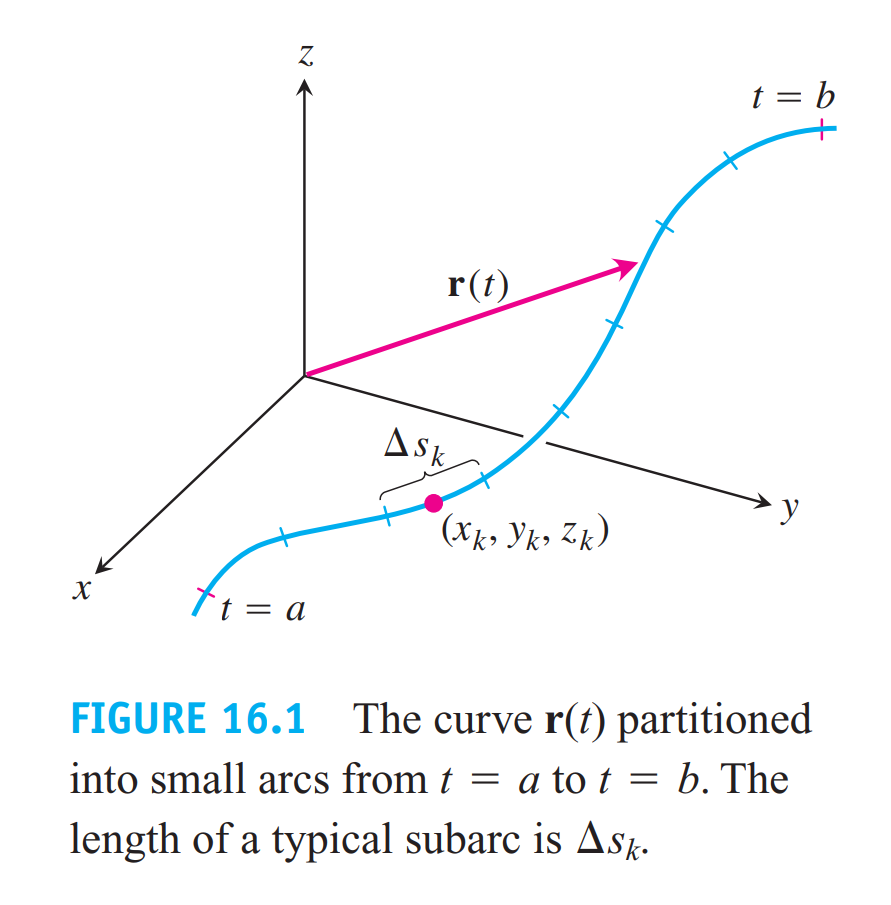
$f(x,y,z)$为积分函数，$L$为积分弧段

性质

满足线性性质，可加性，绝对值不等式

$f(x,y)\le g(x,y)\\ \int_Lf\text ds\le \int_L g\text ds$

计算法

曲线可表示为参数方程，对二维

$\int_Lf\text ds=\int_\alpha^\beta f[\varphi(t),\phi(t)]\sqrt{\varphi'^2(t)+\phi'^2(t)}\text dt$

为使$\text ds\sim\text dt>0$，积分上限总大于积分下限

若可表示为函数或极坐标，则有

$\begin{aligned} s &=\int_{a}^{b}f\sqrt{1+y'^2}\text{d}x\\ &=\int_{\alpha}^{\beta}f\sqrt{\rho^2(\varphi)+\rho'^2(\varphi)}\text{d}\varphi \end{aligned}$

第二类

由变力做功可以得出对坐标的曲线积分

$W=\int_L\vec F\cdot \text d\vec s$

由点积的定义可得

$F=P\vec i+Q\vec j\\ I=\int_LP\text dx+\int_LQ\text dy$

性质

可加性和线性性质都满足

$\int_{L^-}\vec F\cdot \text d\vec s=-\int_{L}\vec F\cdot \text d\vec s$

因为向量有方向所以需要注意曲线积分的方向

计算法

同样利用参数方程换元得到

$I=\int_L[P\varphi'(t)+Q\phi'(t)\text] dt$

对称性，偶零奇倍

若$L$关于$x$，$f$关于y为偶，则

$\int_LP\text dx=0$

若L关于$y=x$对称则

$\int_Lf(x,y)\text dx+\int_Lf(y,x)\text dy=0$

联系

对$\text ds$分解可得到$\text dx,\text dy$

$\int_LP\text dx+Q\text dy=\int_L(P\cos\alpha+Q\cos\beta )\text ds$

在某一弧处的单位切向量为

$\boldsymbol{\tau}=(\cos\alpha,\cos\beta,\cos\gamma)$

有向曲线元为

$\text d\boldsymbol {r}=\boldsymbol{\tau}\text ds=(\text dx,\text dy,\text dz)$

格林公式

对于单连通域(无洞)，定义曲线正向为绕行一直在左边

若满足条件

单连通闭区域$D$
光滑曲线$L$
$P(x,y)$和$Q(x,y)$具有连续偏导数

则有旋度形式

$\iint_{D}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\text dx\text dy=\oint_{\partial D}P\text dx+Q\text dy$

散度形式

$\iint_{D}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right)\text dx\text dy=\oint_{\partial D}P\text dy-Q\text dx$

全微分求积

积分与路径无关，保守场，有

$\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}$

从而要求路径积分只需考虑始末位置，取折线即可

若要找到一个函数$u(x,y)$

$\text du=P\text dx+Q\text dy$

则有

$u_0(x,y)=\int_{x_0}^xP(x,y_0)\text dx+\int_{y_0}^yQ(x,y)\text dy$

全微分方程

若方程为

$P\text dx+Q\text dy=0,\text{find }F(x,y)=0$

满足

$\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}$

则可知$u=C$

$u=C=\int_{(x_0,y_0)}^{(x,y)}P\text dx+Q\text dy$

曲面积分

第一类

$\lambda=\max\{\Delta S_k\}\\ \iint_{\Sigma}f(x,y,z)\text dS=\lim_{\lambda\to0}\sum _if(\xi_i,\eta_i,\zeta _i)\Delta S_i$

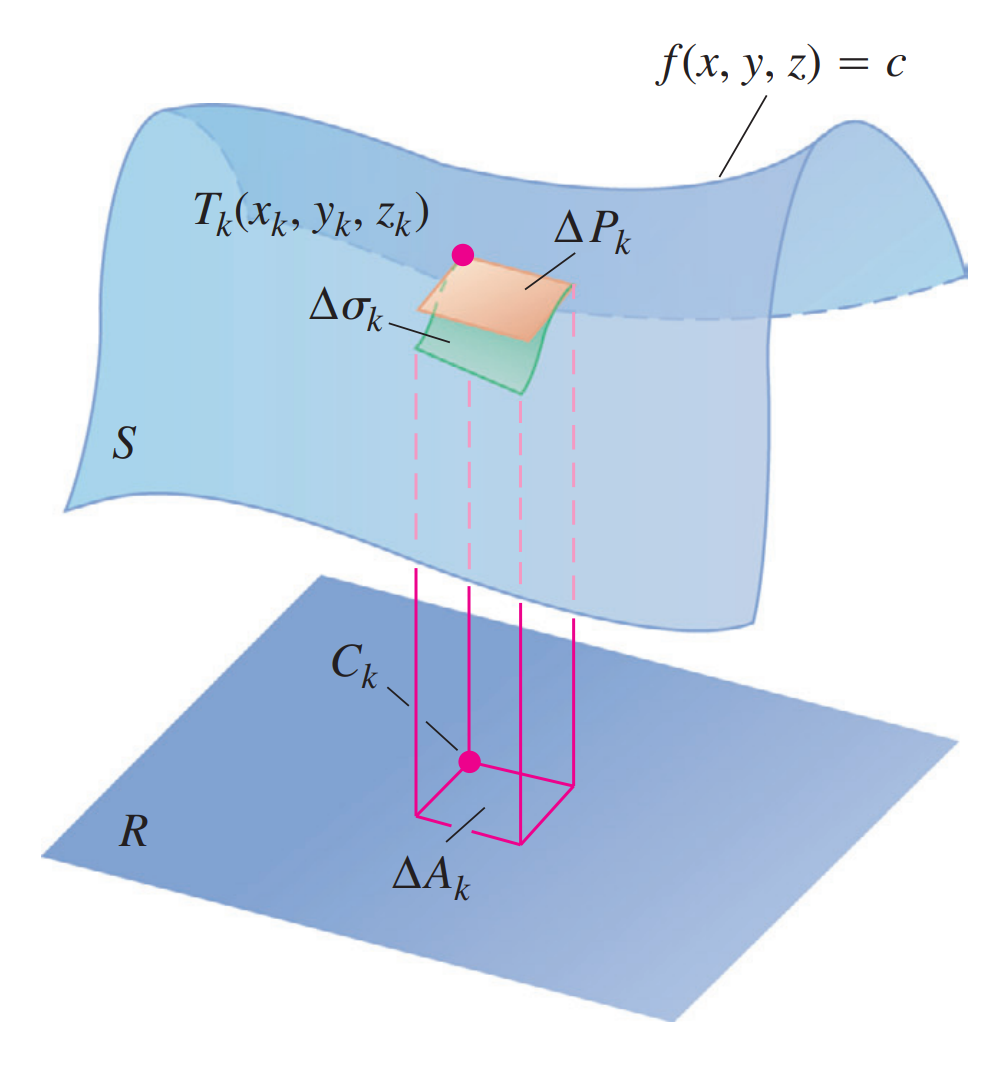
由面积投影定理可以知道

$I=\iint_R\frac {f(x,y,z(x,y))}{|\cos\gamma|}\text dA$

对于一般曲面$f(x,y,z)=c$和方向向量$p$

$\frac1{|\cos\gamma|}=\frac{|\nabla f|}{|\nabla f\cdot p|}\text dA$

特别的，对$z=f(x,y)$

$\nabla f=\left(\frac{\partial z}{\partial x},\frac{\partial z}{\partial y},-1\right)\\ I=\iint_Df\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2}\text dx\text dy$

换元法

对于参数

$\begin{cases}x=x(u,v)\\ y=y(u,v)\\z=z(u,v)\end{cases}$ $I=\int_a^b\text du\int_c^df\begin{Vmatrix} i& j & k\\ x_u& y_u & z_u \\ x_v& y_v & z_v \end{Vmatrix}\text dv\\ I=\int_a^b\text du\int_c^df||e_u\times e_v||\text dv$

或者用雅可比表示

$\sqrt{\frac{\partial(x,y)}{\partial(u,v)}^2+\frac{\partial(y,z)}{\partial(u,v)}^2+\frac{\partial(z,x)}{\partial(u,v)}^2}$

第二类

有向曲面，法向量和轴同向

$(\Delta S)_{xy}=\begin{cases}(\Delta\sigma)_{xy},\cos\gamma>0\\ -(\Delta\sigma)_{xy},\cos\gamma<0\\ 0,\cos\gamma=0\end{cases}$

对于三维向量场

$v=Pi+Qj+Rk$

对某个坐标面

$\iint_{\Sigma}P(x,y,z)\text dy\text dz=\lim_{\lambda\to0}\sum _iP(\xi_i,\eta_i,\zeta _i)(\Delta S_i)_{xy}$

对其余两个面也有同样积分

从而这三个曲面积分称为第二类曲面积分

具有可加性和方向性

计算法

关键是把积分从曲面转化为二重

$\iint_{\Sigma}P(x,y,z)\text dy\text dz=\pm\iint_{D_{yz}}P[x(y,z),y,z]\text dy\text dz$

利用可加性将曲面分成$\cos\gamma$同号的区域

或者换元

$I=\iint_\Sigma\vec v\cdot (e_u\times e_v)\text du\text dv$

对称性，$\Sigma$关于$xOy$对称，$P$关于$z$为偶函数

$\iint_\Sigma P\text dx\text d y=0$

轮换对称

$f(x,y,z)\text dx\text dy=f(y,z,x)\text dy\text dz=f(z,x,y)\text dz\text dx$

联系

$\iint_{\Sigma}P\text dy\text dz+Q\text dz\text dx+R\text dx\text dy=\iint_{\Sigma}(P\cos\alpha+Q\cos\beta+R\cos\gamma)\text dS\\ \iint_{\Sigma}\bold{A}\cdot \text{d}\bold{S}=\iint_{\Sigma}\bold{A}\cdot \bold{n}\text dS$

从而计算时利用

$\frac{\text dy\text dz}{n_x}=\frac{\text dz\text dx}{n_y}=\frac{\text dx\text dy}{n_z}$

换成某一个面的积分

高斯公式

格林公式在三维空间的推广

$\iint_\Sigma P\text dy\text d z+Q\text dz\text d x+R\text dx\text d y=\pm\iiint_\Omega\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)\text dv$

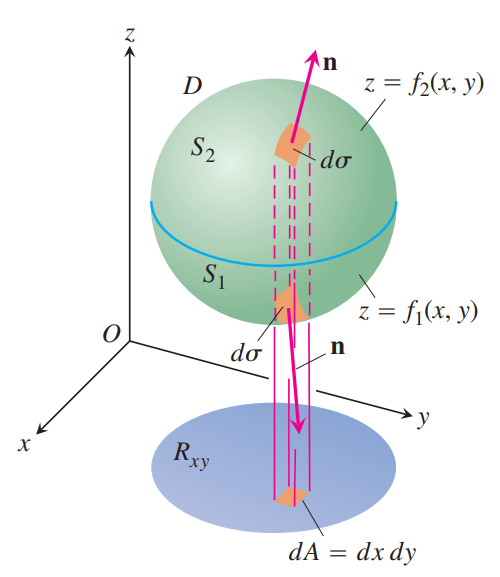
其中外侧为正向，向内为负向

斯托克斯公式

对于三维曲面边界

$\oint _CP\text dx+Q\text dy+R\text dz=\iint_\Sigma\begin{vmatrix} \text dy\text dz& \text dz\text dx & \text dy\text dz\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ P& Q & R \end{vmatrix}$