对于阴极射线的研究发现
洛伦兹力
同上式
从而可以得到磁感应强度
同电场可以定义磁感应线
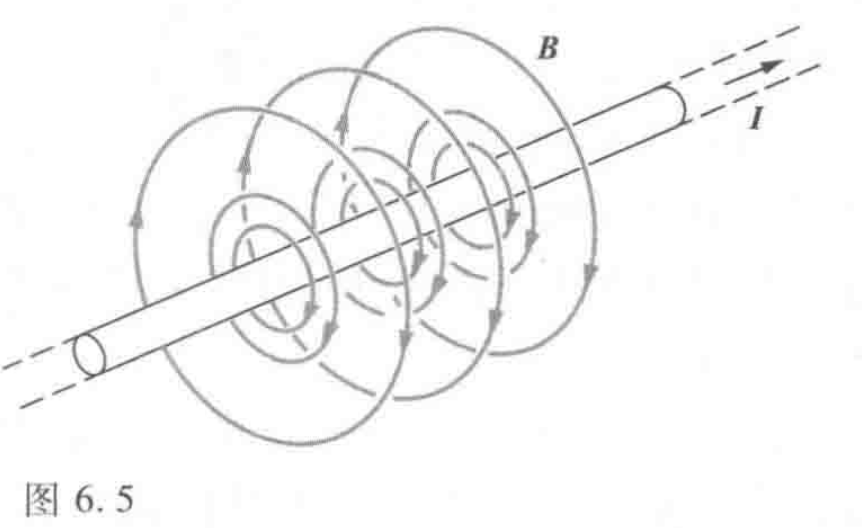
经典结论
对于与磁场方向成一定角度的运动,螺距$h$
电流
引入电流强度
从而电流可以表示成通过个面积元电流的积分电流得到
安培力
对于直导线
对于两平行直导线
磁力偶矩
磁场力做功
毕奥萨伐尔定律
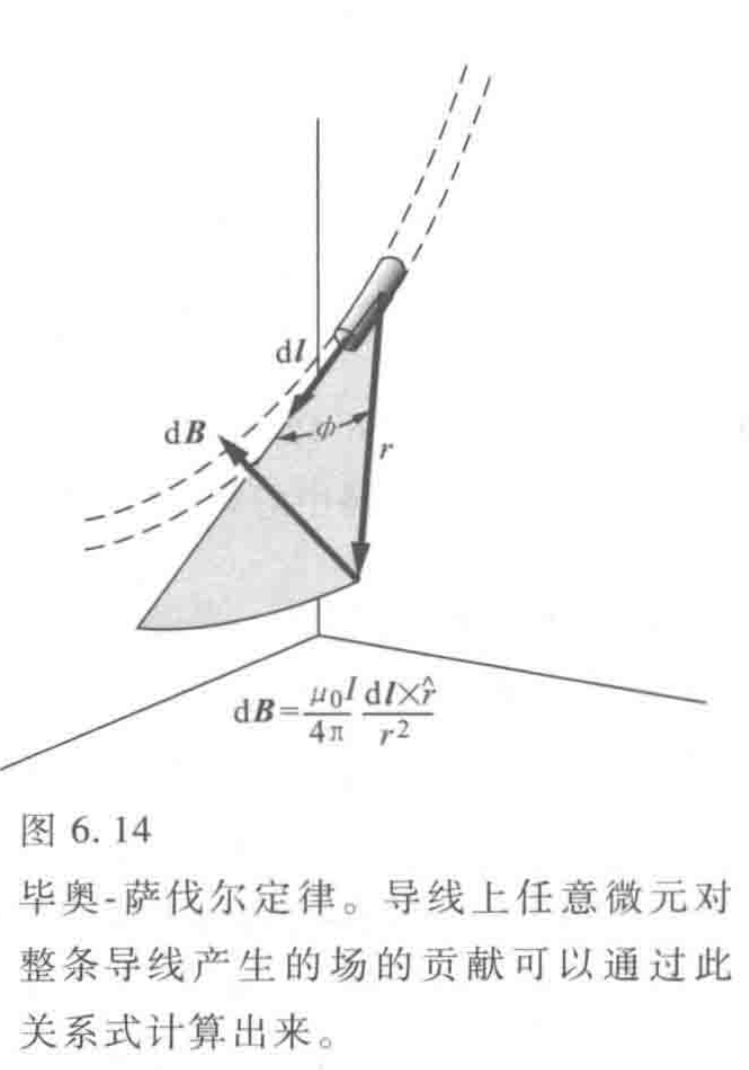
对于电流元$I\text dl$,定律告诉我们
$\mu_0$为真空磁导率
应用
常见的磁场
导线
无限长
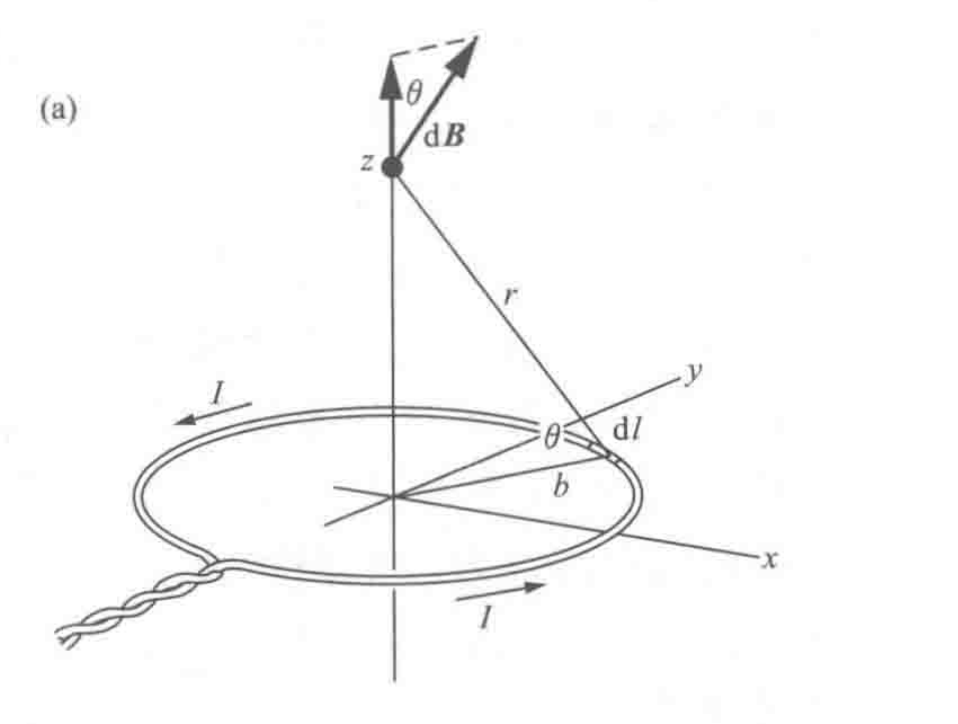
对于$x=0$处
若远离
引入磁矩
这就是磁偶极磁场
运动电荷,有
高斯定理
磁场的散度为零
所以有
安培环路定理
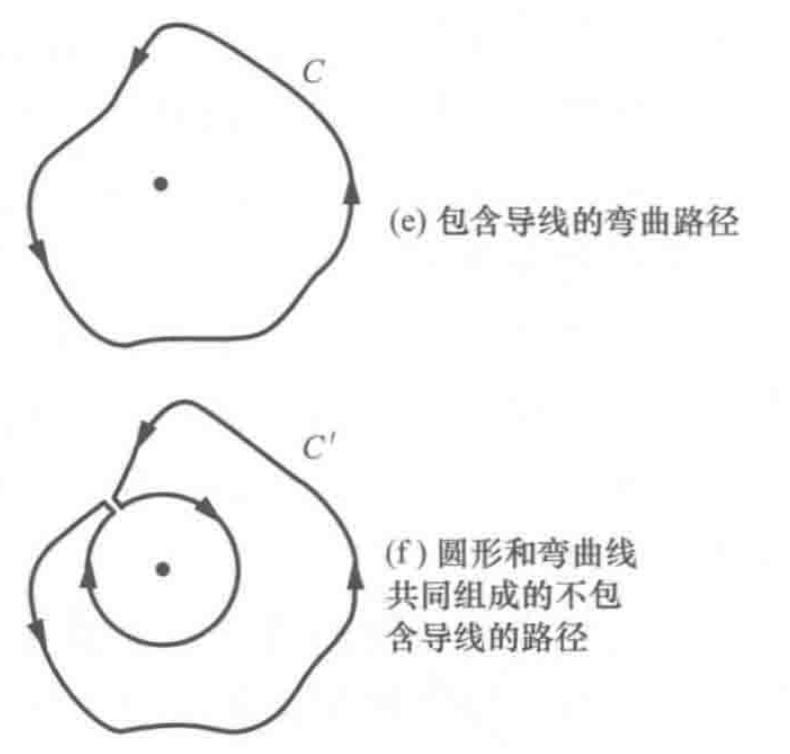
电流方向符合使用右手定则得到的绕行方向时为正
安培力
电流是由大量带电粒子定向运动而形成的,由洛伦兹力可以得到
对于最基本的直线电流
对于两根长直导线
磁力矩
对于线圈来说在磁场中会受力产生力矩
其中$\vec{e_n}$的方向由右手定则确定
对于法向量与磁场方向的夹角$\theta$
- $\theta=0^{\circ}$线圈不受磁力偶矩的作用此时线圈处于稳定平衡状态
- $\theta=90^{\circ}$线圈所受磁力偶矩最大
- $\theta=180^{\circ}$线圈处于不稳定平衡状态
对安培力做功无论是平动还是转动
磁介质
类比电介质我们引入磁介质和相对磁导率
戒指内部任意点的磁场强度$B$可表示为外磁场$B_0$和附加磁场$B’$的矢量和
- $\mu_r>>1$铁磁性磁场被大大增强
- $\mu_r>1$顺磁性磁场被加强
- $\mu_r<1$ 抗磁性磁场被削弱
- $\mu_r=0$完全抗磁性磁场被抵消
为了描述磁介质的被磁化强度,我们引入磁化强度
在宏观上石戒指可在表面形成等效环形电流称为磁化电流
类比$P_n=\sigma$
$j_s$称为磁化面电流线密度,故对于安培定理
定义$H$ 为磁场强度
对于各向同性的均匀磁介质
其中$\chi _m$为磁化率,$\mu_r$称为相对磁导率,$\mu$为磁导率
引入位移电流
这就是全电流的安培环路定理二分,位移电流同磁化电流没有热效应
电磁感应
对$\Phi$求导得到两个分量
分别为动生和感生电动势
自感
互感
自感$L$和互感$M$单位都为亨利
一般的
能量
所以有能量密度
对于自感,有