有限差分

Forward

$\frac{\text{d}f}{\text dt}=\frac{f(t_0+\Delta t)-f(t_0)}{\Delta t}$

Backward

$\frac{\text{d}f}{\text dt}=\frac{f(t_0)-f(t-\Delta t)}{\Delta t}$

更精确(二阶)

$\frac{\text{d}f}{\text dt}=\frac{f(t_0+\Delta t)-f(t_0-\Delta t)}{2\Delta t}$

二阶导数

$\frac{\text{d}^2f}{\text dt^2}=\frac{f(t_0+\Delta t)+f(t_0-\Delta t)-2f(t_0)}{\Delta t^2}$

理查森外推公式

对于某个带误差的式子

$Q=F(h)+kh^n$

再加入一个方程可以得到

$Q=\frac{2^nF(h/2)-F(h)}{2^n-1}$

插值

拉格朗日

$L_{n-1}(x)=\sum_{k=0}^{n-1}y_k\frac{\displaystyle\prod_{j\ne k}(x-x_j)}{\displaystyle\prod_{j\ne k}(x_k-x_j)}\\ p(x)=\prod_{j\ne k}(x-x_j)$

缺点：在一堆原始点中，只改变了其中几个点的情况下，所有的基函数和插值曲线都要重新计算

牛顿

差商

$f[x_0]=f(x_0)\\ f[x_0,x_1]=\frac{f[x_1]-f[x_0]}{x_1-x_1}\\ f\left[x_{0}, x_{1}, \cdots, x_{n}\right]=\frac{f\left[x_{1}, x_{2}, \cdots, x_{n}\right]-f\left[x_{0}, x_{1}, \cdots, x_{n-1}\right]}{x_{n}-x_{0}}$

则有牛顿插值公式

$\begin{array}{l} f(x)=f\left[x_{0}\right]+f\left[x_{0}, x_{1}\right]\left(x-x_{0}\right) \\ +f\left[x_{0}, x_{1}, x_{2}\right]\left(x-x_{0}\right)\left(x-x_{1}\right)+\ldots \\ +f\left[x_{0}, x_{1}, \ldots, x_{n}\right]\left(x-x_{0}\right)\left(x-x_{1}\right) \ldots\left(x-x_{n-1}\right) \end{array}$

数值积分

Trapezoid

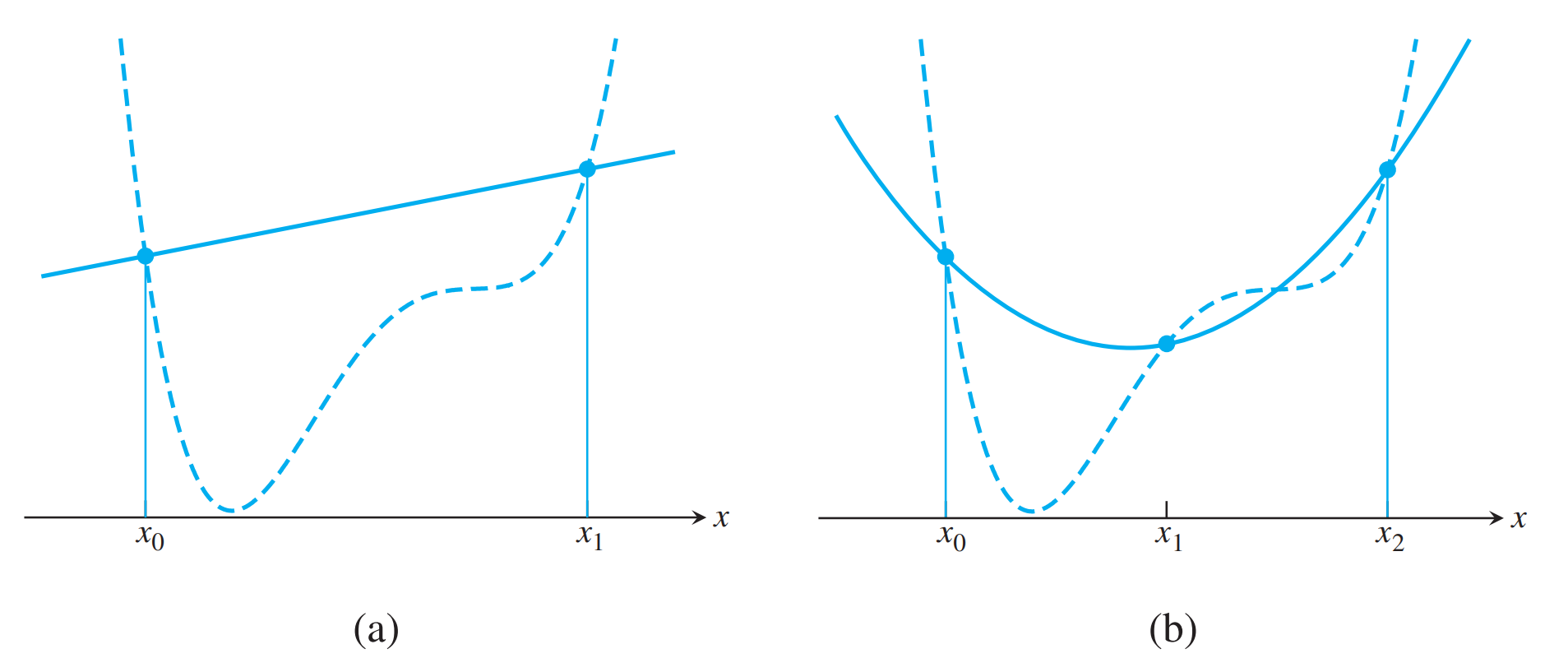
用四边形进行逼近，如图$(a)$

$\int_{x_0}^{x_1}f(x)\text dx=h\left [\frac{f(x_1)+f(x_0)}2\right]$

每两个点进行采样，从而有

$\int_{a}^{b}f(x)\text dx=\frac h2\left [f(a)+f(b)+2\sum_{i=1}^{m-1}f(x_i)\right]-\sum_{i=1}^{m-1}\frac{h^3}{12}f''(c_i)$

由广义介值定理

$f(x)\sum_{i=1}^na_i=\sum_{i=1}^na_i f(x_i)\\ \sum_{i=1}^{m-1}\frac{h^3}{12}f''(c_i)=\frac{h^2(b-a)}{12}f''(c)$

Simpson

用二次函数来插值三个点，积分得

$\int_{x_0}^{x_2}f(x)\text dx=\frac h3(y_0+4y_1+y_2)-\frac{h^5}{90}f^{(5)}(c)$

从而对于区间$[a,b]$

$\int_{a}^{b}f(x)\text dx=\frac h3\left [f(x_0)+f(b)+2\sum_{i=1}^{m-1}f(x_{2i})+4\sum_{i=1}^{m}f(x_{2i-1})\right]$

龙贝格

Romberg Integration

利用外推公式和增加细分

$h_j=\frac{b-a}{2^{j-1}}\\ R_{j,1}=\frac 12R_{j-1,1}+h_j\sum_{i=1}^{2^{j-1}}f[a+(2j-1)h_j]\\ R_{j,k}=\frac{4^{k-1}R_{j,k-1}-R_{j-1,k-1}}{4^{k-1}-1}$

自适应

Adaptive Quadrature

如果使用Simpson方法

$\text {error}=\frac 1{15}\left[S(a,b)-S\left(a,\frac{a+b}2\right)-S\left(\frac{a+b}2,b\right)\right]$

二维

用网格来表示

偏微分方程

对于$u(x,y)$

$Au_{x x} + Bu_{x y} + Cu_{yy} + F(u_x ,u_y ,u, x, y) = 0$

利用前面的公式固定一个变量，有

$u_{x x}(x, t) \approx \frac{1}{h^{2}}(u(x+h, t)-2 u(x, t)+u(x-h, t))$

对于热传导方程，使用Forward Difference Method

$u_t=Du_{xx}\\\sigma =\frac{Dk}{h^2}\\ \\w_{i,j+1}=\sigma w_{i+1,j}+(1-2\sigma)w_{i,j}+\sigma w_{i-1,j}$

如果直接能从前面的值推算出后面的值则为显式

写成矩阵形式$w{j+1} = Aw{j} + s_j$

$\left[\begin{array}{c} w_{1, j+1} \\ \vdots \\ w_{m, j+1} \end{array}\right]=\left[\begin{array}{ccccc} 1-2 \sigma & \sigma & 0 & \cdots & 0 \\ \sigma & 1-2 \sigma & \sigma & \ddots & \vdots \\ 0 & \sigma & 1-2 \sigma & \ddots & 0 \\ \vdots & \ddots & \ddots & \ddots & \sigma \\ 0 & \cdots & 0 & \sigma & 1-2 \sigma \end{array}\right]\left[\begin{array}{c} w_{1 j} \\ \vdots \\ w_{m j} \end{array}\right]+\sigma\left[\begin{array}{c} w_{0, j} \\ 0 \\ \vdots \\ 0 \\ w_{m+1, j} \end{array}\right]$

显式具有不稳定性，误差容易爆炸

隐式

使用Backward来计算导数可以得到

$-\sigma w_{i+1,j}-\sigma w_{i-1,j}+(1+2\sigma)w_{i,j}= w_{i,j-1}$ $\left[ \begin{array} { c c c c c } { 1 + 2 \sigma } & { - \sigma } & { 0 } & { \cdots } & { 0 } \\ { - \sigma } & { 1 + 2 \sigma } & { - \sigma } & { \ddots } & { \vdots } \\ { 0 } & { - \sigma } & { 1 + 2 \sigma } & { \ddots } & { 0 } \\ { \vdots } & { \ddots } & { \ddots } & { \ddots } & { - \sigma } \\ { 0 } & { \cdots } & { 0 } & { - \sigma } & { 1 + 2 \sigma } \end{array} \right] \left[ \begin{array} { c } { w _ { 1 j } } \\ { \vdots } \\ { w _ { m j } } \end{array} \right] = \left[ \begin{array} { c } { w _ { 1 , j - 1 } } \\ { \vdots } \\ { w _ { m , j - 1 } } \end{array} \right] + \sigma \left[ \begin{array} { c } { w _ { 0 j } } \\ { 0 } \\ { \vdots } \\ { 0 } \\ { w _ { m + 1 , j } } \end{array} \right]$