函数

多元函数

$w=f(x_1,x_2,\dots,x_n)$

二元函数

$f(x,y)$

定义域

$w=\sqrt{y-x^2},y\ge x^2$

去心邻域

$\mathring{U}(P_0,\delta)=\{P|0<|PP_0|<\delta\}$

若存在某邻域使得$U(P)\subset R$则为内点，反之为外点

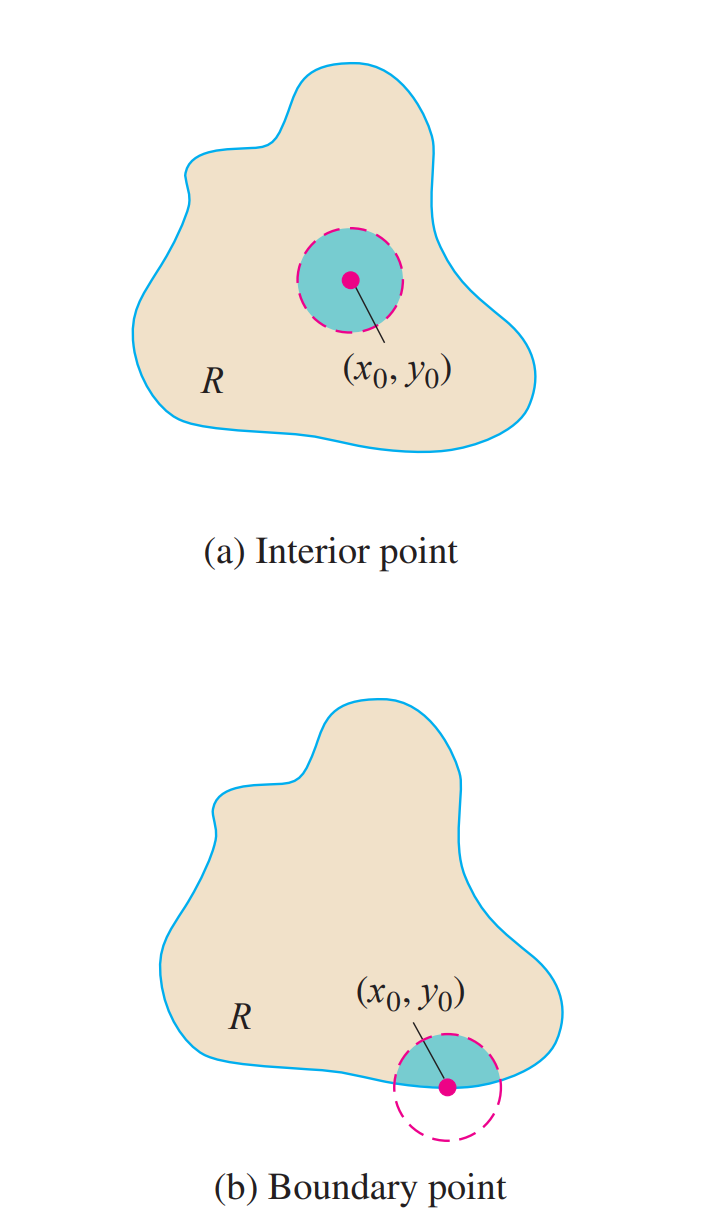
若有一部分属于，一部分不属于则为边界点

若所有的点都为内点则为开集，若边界$\partial R\subset R$则为闭集

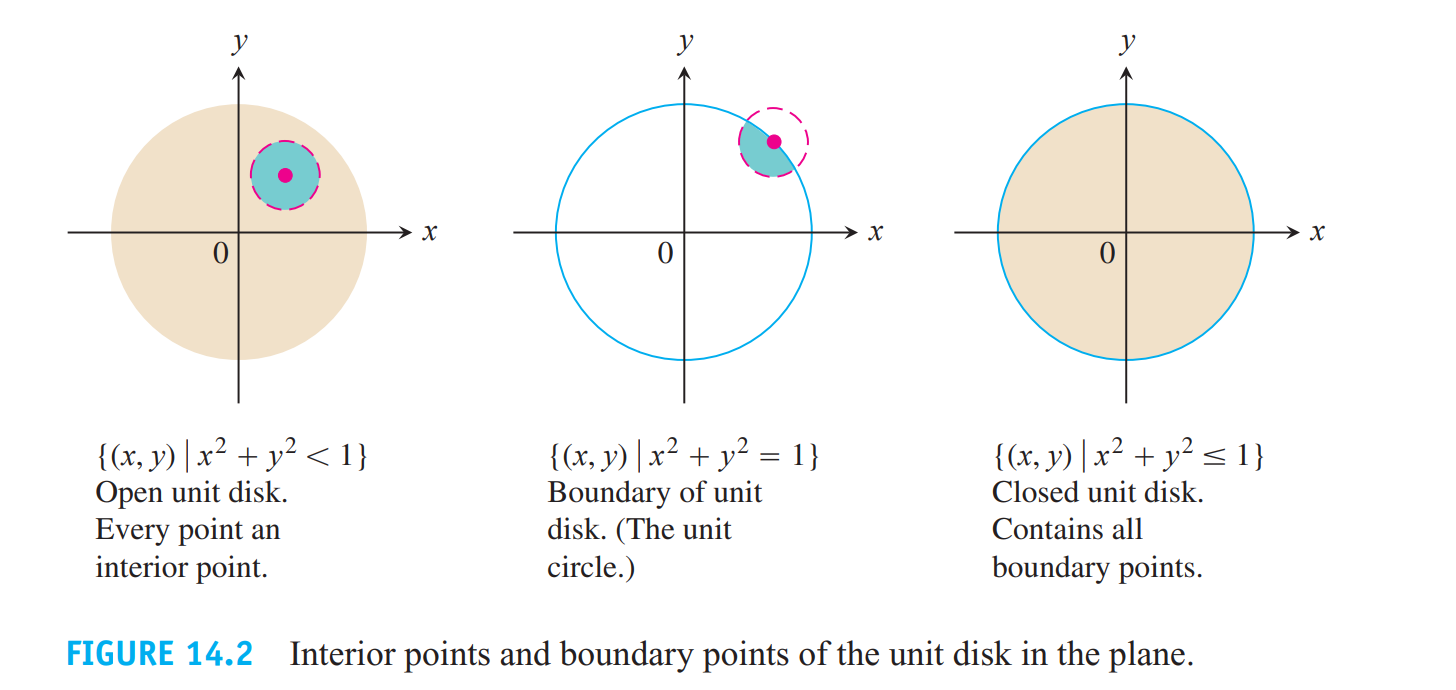
若存在$r>0$使得

$R\subset U(O,r)$

则为有界集

$y\ge x^2$为封闭无界集

满足$f(x,y)=c$的线为等值线(Level Curve)

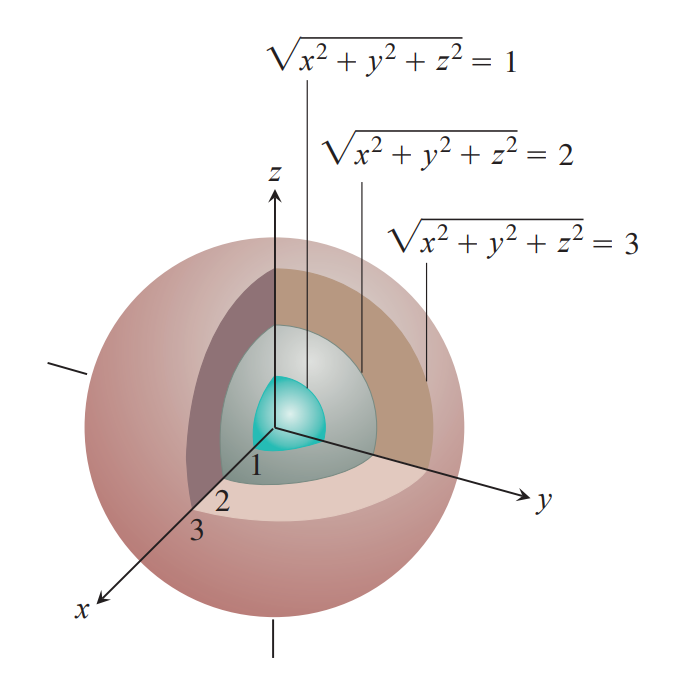
满足$f(x,y,z)=c$的面为等值面(Level Surface)

微分

偏导数

固定一个然后求导

To distinguish partial derivatives from ordinary derivatives we use the symbol $\partial$ rather than the $\text d$ previously used

$\frac{\partial f}{\partial x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x, y_{0}\right)-f\left(x_{0}, y_{0}\right)}{\Delta x}$

高阶

$\frac{\partial^{2} f}{\partial x^{2}}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right), \quad \frac{\partial^{2} f}{\partial x \partial y}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)$

杨氏定理(Young’s theorem)，二阶偏微分连续，二阶混合偏导数相等

$\frac{\partial^{2} f}{\partial x \partial y}=\frac{\partial^{2} f}{\partial y \partial x}$

可偏(有偏导数)不代表有全微分形式

全微分

$\text{d}z=\frac{\partial f}{\partial x}\text{d}x+\frac{\partial f}{\partial y}\text{d}y$

从而有标准线性近似

$f(x,y)\approx f(x_0,y_0)+f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)=L(x,y)$

对于误差$E(x,y)=f(x,y)-L(x,y)$

$|E(x,y)|\le\frac12M(|x-x_0|+|y-y_0|)^2\\ M=\max\{|f_{xx}|,|f_{yy}|,|f_{xy}|\}$

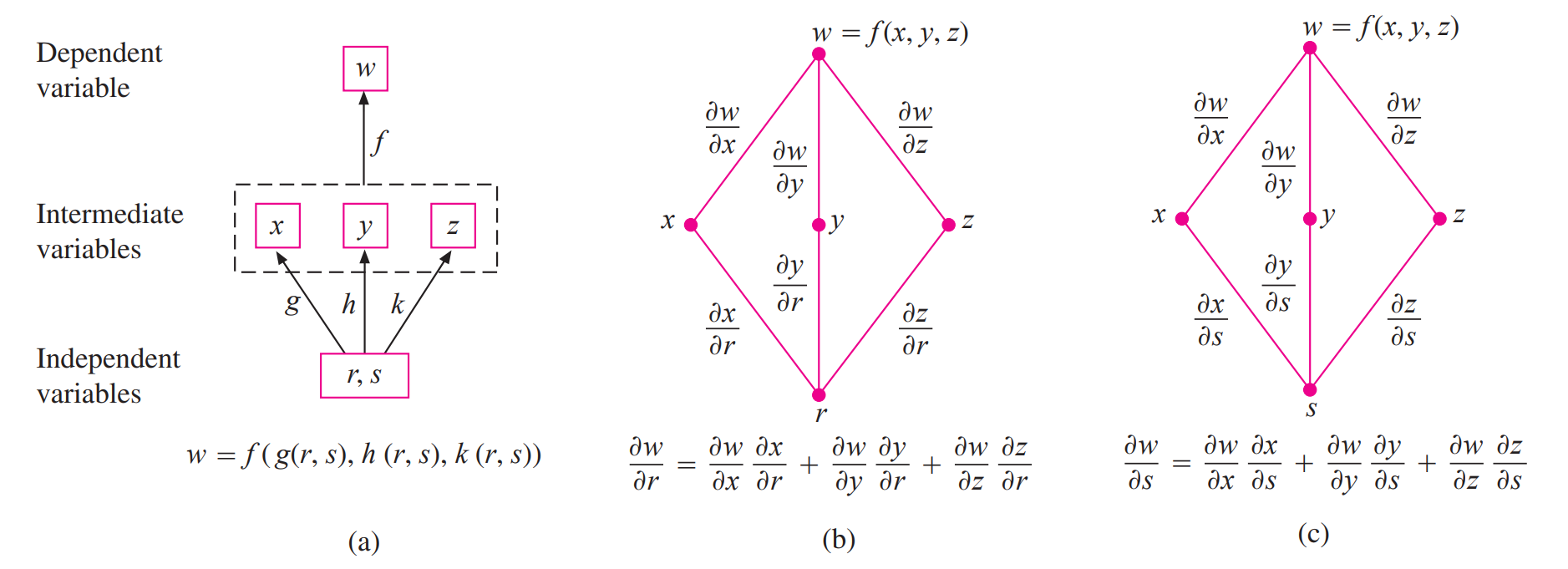
链式法则

复合函数

$x\overset{f_0 }{\rightarrow}x^1\to\cdots\overset{f_k }{\rightarrow}y\\ f=f_k^{\circ}f_{k-1}^{\circ}\dots^{\circ}f_0$

利用全微分可以得到链式法则

$w=f(x(t),y(t))\\ \frac{\partial w}{\partial t}=\frac{\partial f}{\partial x}\frac{\partial f}{\partial t}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial t}$

更一般的

$\frac{\partial w}{\partial r}=\frac{\partial w}{\partial x} \frac{\partial x}{\partial r}+\frac{\partial w}{\partial y} \frac{\partial y}{\partial r}+\frac{\partial w}{\partial z} \frac{\partial z}{\partial r} \\ \frac{\partial w}{\partial s}=\frac{\partial w}{\partial x} \frac{\partial x}{\partial s}+\frac{\partial w}{\partial y} \frac{\partial y}{\partial s}+\frac{\partial w}{\partial z} \frac{\partial z}{\partial s}$

隐函数

首先，有方程

$F(x,y,z)=0$

从而若$F_z\ne 0$可以确定一个函数$z(x,y)$

由方程推导法(两边直接对$x,y$求导)

或用公式

$\frac{\partial z}{\partial x}=-\frac{F_x}{F_z} \\ \frac{\partial z}{\partial y}=-\frac{F_y}{F_z}$

利用全微分可以将两个导数同时求出

方程组

$\begin{cases}F(x,y,u,v)=0\\ G(x,y,u,v)=0\end{cases}$

如果

$J=\frac{\partial(F,G)}{\partial(u,v)}=\begin{vmatrix}\frac{\partial F}{\partial u}&\frac{\partial F}{\partial v}\\\frac{\partial G}{\partial u}&\frac{\partial G}{\partial v}\end{vmatrix} \ne0$

则可以确定$u(x,y)$和$v(x,y)$，一个方程确定一个因变量

将要求的因变量用自变量替换得到

$\frac{\partial u}{\partial x}=-\frac1J\frac{\partial(F,G)}{\partial(x,v)}=-\frac1J\begin{vmatrix}\frac{\partial F}{\partial x}&\frac{\partial F}{\partial v}\\\frac{\partial G}{\partial x}&\frac{\partial G}{\partial v}\end{vmatrix}$

同理也有方程推导法和微分法

根据克拉姆法则，对于一个$n$元线性方程组，如果它的系数矩阵的行列式不等于零，则可以使用如下公式求解：

$x_i = \Delta_i / \Delta$

其中，$x_i$是第$i$个未知数的值，$\Delta_i$是将系数矩阵中第$i$列替换为常数矩阵后的行列式值，$\Delta$是系数矩阵的行列式值。

方向导数

方向导数为函数在某一方向(正反都可以)上的变化率

$\frac{\partial f}{\partial l}=\lim _{s \rightarrow 0} \frac{f\left(x_{0}+sl_x, y_{0}+sl_y\right)-f\left(x_{0}, y_{0}\right)}{s}$

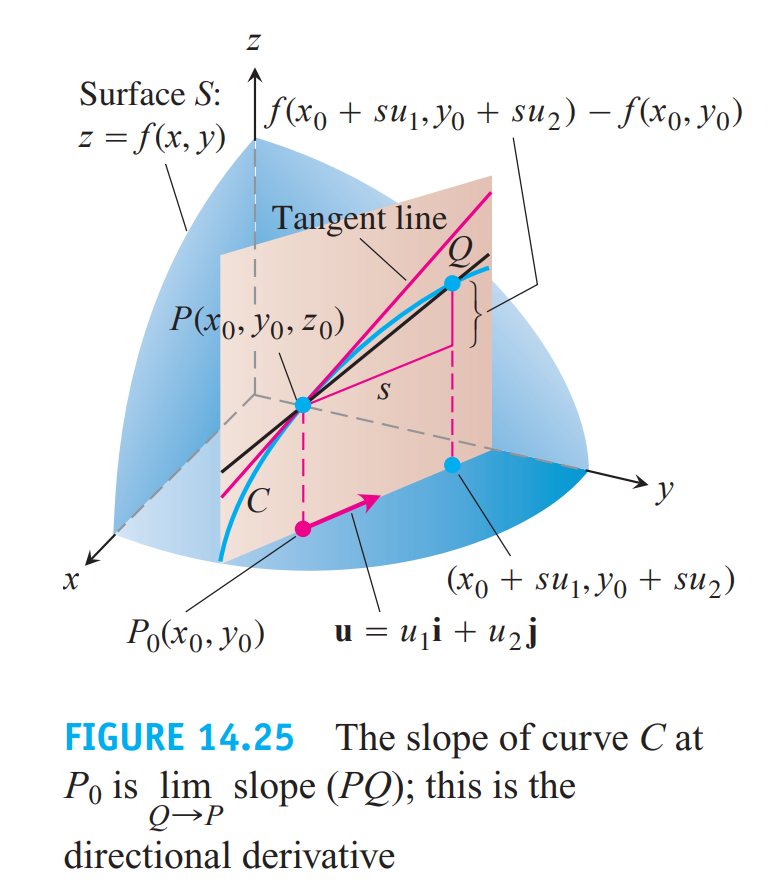
定义$l$的方向余弦为

$\cos\alpha=\frac{\Delta x}{\Delta l},\cos\alpha=\frac{\Delta y}{\Delta l}$

由全微分公式将导数沿方向分解，得到

$\left. \frac{\partial f}{\partial l}\right|_{x_0,y_0}=\frac{\partial f}{\partial x}\cos\alpha+\frac{\partial f}{\partial y}\cos\beta\\ \text d f=(\nabla f\cdot \vec l)\text d s$

梯度

定义梯度，Nabla算子

$\text{grad}f=\nabla f(x,y)=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)$

利用辅助角公式得出梯度方向的方向导数最大，或

$\left. \frac{\partial f}{\partial l}\right|_{x_0,y_0}=\nabla f(x,y)\cdot(\cos\alpha,\cos\beta)$

所以梯度指向上升最快的方向

可以看出梯度向量垂直于等高线的切线

$\nabla (kf)=k\nabla f\\ \nabla(f\pm g)=\nabla f\pm \nabla g\\ \nabla (fg)=\nabla fg+f\nabla g\\ \nabla\left(\frac fg\right)=\frac{\nabla fg-f\nabla g}{g^2}$

切线和法线

引入等值面$f(x,y)=c$，对于空间曲线引入参数$t$后得到

$\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)\cdot\left(\frac{\partial x}{\partial t},\frac{\partial y}{\partial t}\right)=2 \frac{\partial f}{\partial t}=0$

梯度向量垂直于等值面，梯度的模为沿梯度方向的方向导数

对于切线

$\frac{x-x_0}{\varphi'(t_0)}=\frac{y-y_0}{\phi'(t_0)}=\frac{z-z_0}{\omega'(t_0)}$

法平面为与切线垂直的面

${\varphi'(t_0)}(x-x_0)={\phi'(t_0)}(y-y_0)={\omega'(t_0)}(z-z_0)$

对于由方程确定的曲线

$\begin{cases}F(x,y,z)=0\\ G(x,y,z)=0\end{cases}\\ J=\frac{\partial(F,G)}{\partial(y,z)}$

则以$x$为参数可以写成

$\begin{cases}x=x\\ y=y(x)\\z=z(x)\end{cases}$

解出

$T=(1,y_x,z_x)$

整理得轮换对称式

$T=\left(\begin{vmatrix}F_y&F_z\\ G_y& G_z\end{vmatrix}_M,\begin{vmatrix}F_z&F_x\\ G_z& G_x\end{vmatrix}_M,\begin{vmatrix}F_x&F_y\\ G_x& G_y\end{vmatrix}_M\right)$

推广到三维空间，切向量

$T=(F_x,F_y,F_z)=(-z_x,-z_y,1)$

切平面

$f_{x}\left(P_{0}\right)\left(x-x_{0}\right)+f_{y}\left(P_{0}\right)\left(y-y_{0}\right)+f_{z}\left(P_{0}\right)\left(z-z_{0}\right)=0$

法线

$x=x_{0}+f_{x}\left(P_{0}\right) t, \quad y=y_{0}+f_{y}\left(P_{0}\right) t, \quad z=z_{0}+f_{z}\left(P_{0}\right) t$

可以方便地使用全微分公式得到

极值和最值

$n$ 元函数 $f(x_1,x_2,\ldots,x_n)$，若存在某个自变量取值的去心邻域，在该邻域内函数值不小于（或不大于）该自变量取值处的函数值，则称该自变量取值处为函数的极大值点（或极小值点）

必要条件

一阶偏导数都为$0$

$f_x(x,y)=0,f_y(x,y)=0$

充分条件

引入Hessian 矩阵

$H=\begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n}\\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n}\\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}$

对于二元

$f_{xx}=A,f_{xy}=B,f_{yy}=C$

若$AC-B^2>0$则有极值，$A/C>0$则为极小值

若$AC-B^2<0$则无极值，$AC-B^2=0$则可能有

拉格朗日函数

对于约束条件$g(x_1,x_2,\dots,x_n)=0$，可以构造拉格朗日函数 $L(x_1,x_2,\dots,x_n)=f(x_1,x_2,\dots,x_n)+\lambda g(x_1,x_2,\dots,x_n)$

$\begin{cases} \frac{\partial L}{\partial x_1} = 0\\ \frac{\partial L}{\partial x_2} = 0\\ \cdots\\ \frac{\partial L}{\partial x_n} = 0\\ \frac{\partial L}{\partial \lambda} = 0\\ \end{cases}$

需要注意的是，拉格朗日乘数法并不适用于所有类型的优化问题，有些问题可能存在多个局部极小值或不可导等情况，需要根据具体问题进行分析