大一/复变函数/积分

引入

考虑复变函数$w(t)$

$$w(t) = u(t) + \text iv(t)$$

对其求导得到

$$w'(t) = u'(t) + \text iv'(t)\\ \frac{\text d} {\text dt }e^{z_0t}=z_0e^{z_0t}$$

同理，有

$$\int_a^bw(t)\text dt=\int_a^bu(t)\text dt+\text i\int_a^bv(t)\text dt$$

从而我们可以分别对实部和虚部进行积分

$$\Re\int_a^bw(t)\text dt=\int_a^b\Re [w(t)]\text dt\\ \Im\int_a^bw(t)\text dt=\int_a^b\Im [w(t)]\text dt$$

所以微积分基本定理也可以使用

$$\left.{\int_a^bw(t)\text dt=W(t)}\right|_a^b$$

如

$$\int_0^{\frac\pi 4}e^{\text it}\text dt=\frac{\sqrt 2}2+\left(1-\frac{\sqrt 2}2\right)\text i$$

注意，如积分中值定理不适用于复变函数

曲线

$$z(t) = x(t) + \text iy(t)\quad (t\in[a,b])$$

这就是曲线$C$的方程

• 若$z$值没有重复相交则为简单曲线(simple arc)
• 只有$z(a)=z(b)$则称为简单封闭曲线(simple closed curve)

弧微分

$$\text d s=\sqrt{1+y'^2}\text dx=\sqrt{[x'(t)]^2+[y'(t)]^2}\text d t$$

所以弧长

$$L=\int_a^b\sqrt{[x'(t)]^2+[y'(t)]^2}\text d t$$

对于$\varphi’(\tau)>0$，也可变换

$$Z(t)=z(\varphi(t))$$

又因为

$$|z'(t)|=\sqrt{[x'(t)]^2+[y'(t)]^2}\\ L=\int_\alpha^\beta|z'(\varphi(t))|\varphi'(t)\text d t=\int_\alpha^\beta|Z'(t)|\text d t$$

考虑径矢

$$\mathbf{T}=\frac{z'(t)}{|z'(t)|}$$

如果$z’(t)$连续且$\ne0$，即$x’(t),y’(t)$不同时为$0$

则曲线处处有切线可以自由转动，则曲线光滑

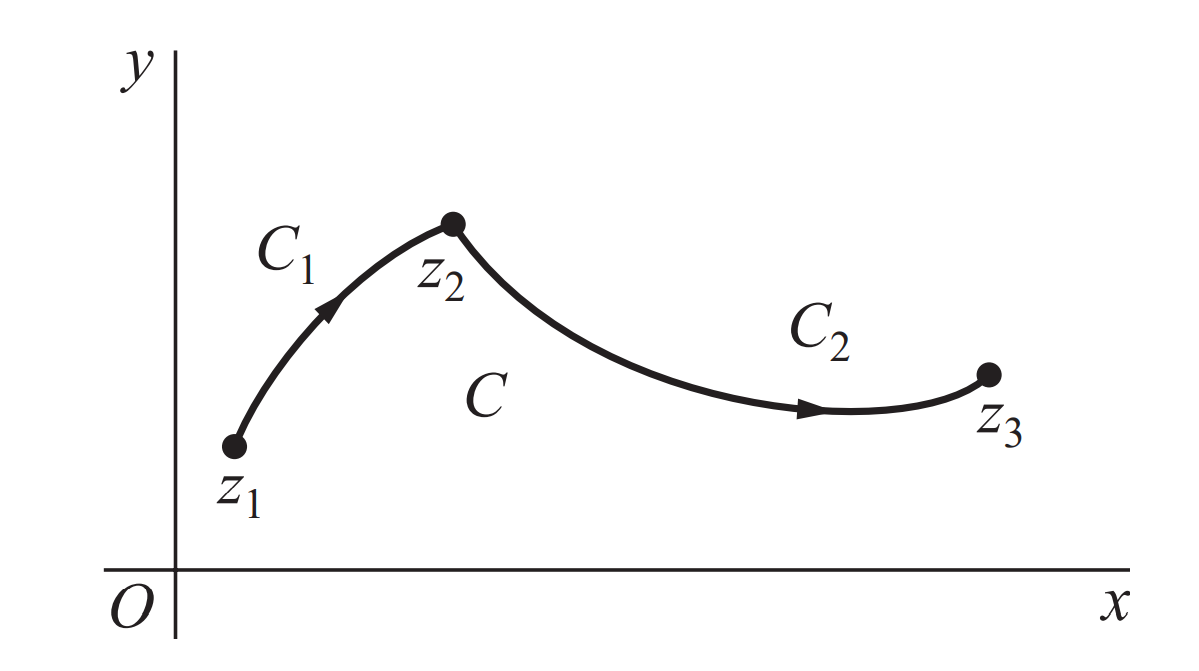
轮廓

contour通常指的是复平面上的曲线，它可以用于描述复变函数在复平面上的取值和变化情况，用两种方式定义

1. 参数方程：$z (t)$，其中 $t$ 是在某个区间 $[a,b]$ 上变化的实数。通过让 $t$ 在区间 $[a,b]$ 上遍历，我们就可以得到一条曲线
2. 等值线方程：$f(z) = c$，其中 $c$ 是一个常数。这个方程表示的是函数 $f(z)$ 在复平面上取值为 $c$ 的所有点

积分

对于一个轮廓$C$，积分表示为

$$\int_Cf(z)\text dz\;\;\text{or}\;\;\int_{z_1}^{z_2}f(z)\text dz$$

对于由参数定义的$C$

$$\int_Cf(z)\text dz=\int_Cf[z(t)]z'(t)\text dt$$

性质

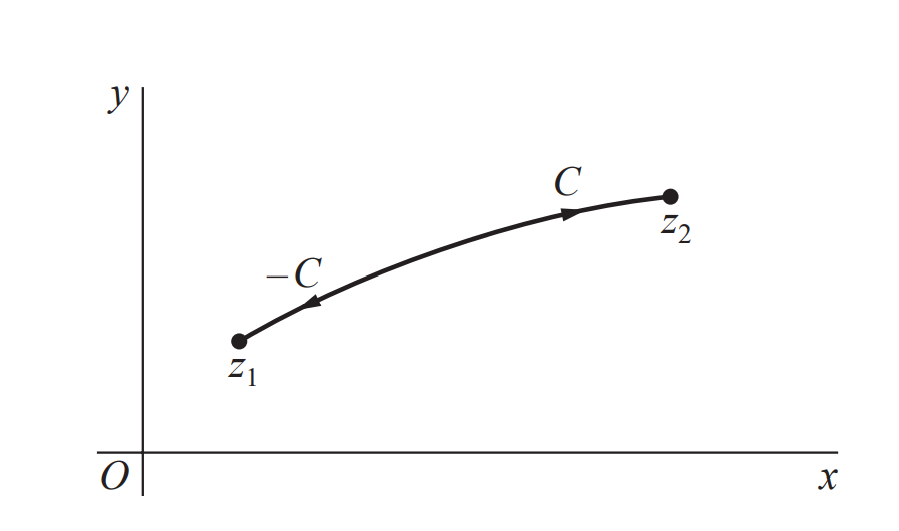
对于方向相反的轮廓$z(-t)$

$$\int_{-C}f(z)\text dz=-\int_Cf(z)\text dz$$

可加性

$$\int_Cf(z)\text dz=\int_{C_1}f(z)\text dz+\int_{C_2}f(z)\text dz$$