概念

类比一般函数复变函数就是将一个复数映射成另外一个复数

$w=f(z)\\ u+v\text{i}=f(x+y\text{i})\\ f(z)=u(x,y)+v(x,y)\text{i}=f(re^{\text{i}\theta})$

如平方根

$f(z)=\sqrt{r}\exp\left(\frac{\theta}2\text{i}\right)$

相较于定义在实数域上的函数，复变函数没有图像

从变换的角度来思考，函数将平面上的每一个点映射到了另外一个点

例如反射，旋转等变换

可视化

通过对于特殊曲线的变换来可视化

$f(z)=z^2\\ \begin{cases}u=x^2-y^2\\ v=2xy\end{cases}$

$e^z=e^{x+y\text{i}}=e^xe^{y\text{i}}$

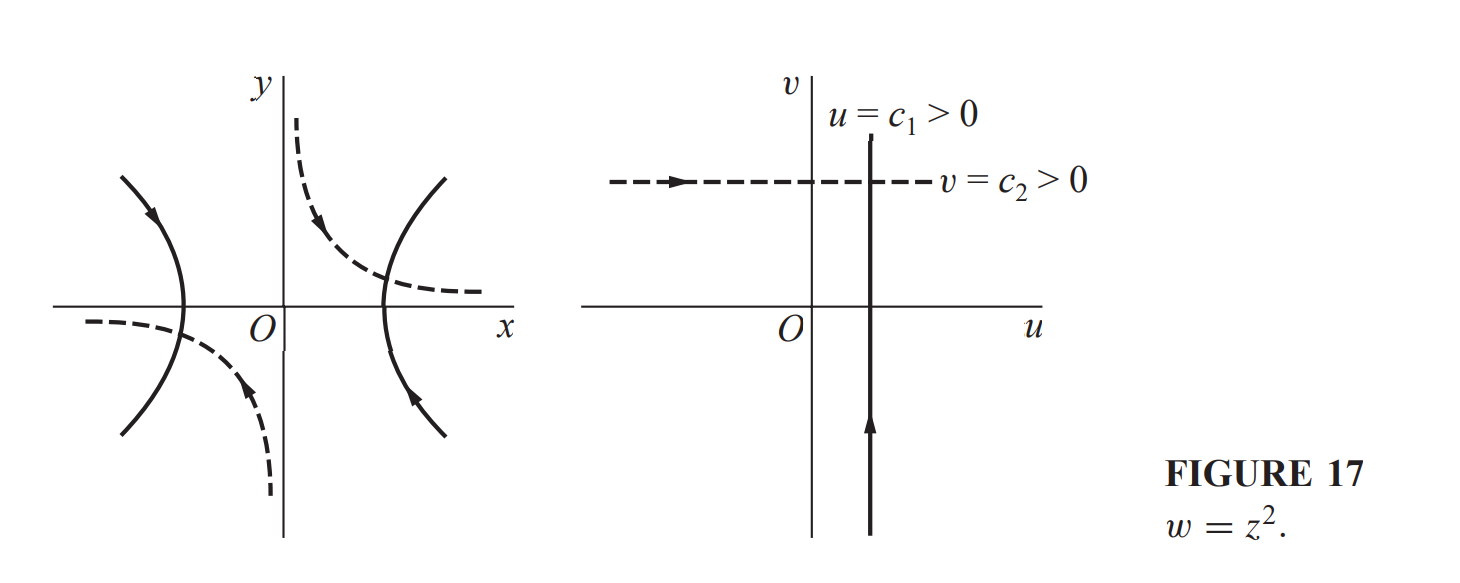
通过指数形式也可表示变换

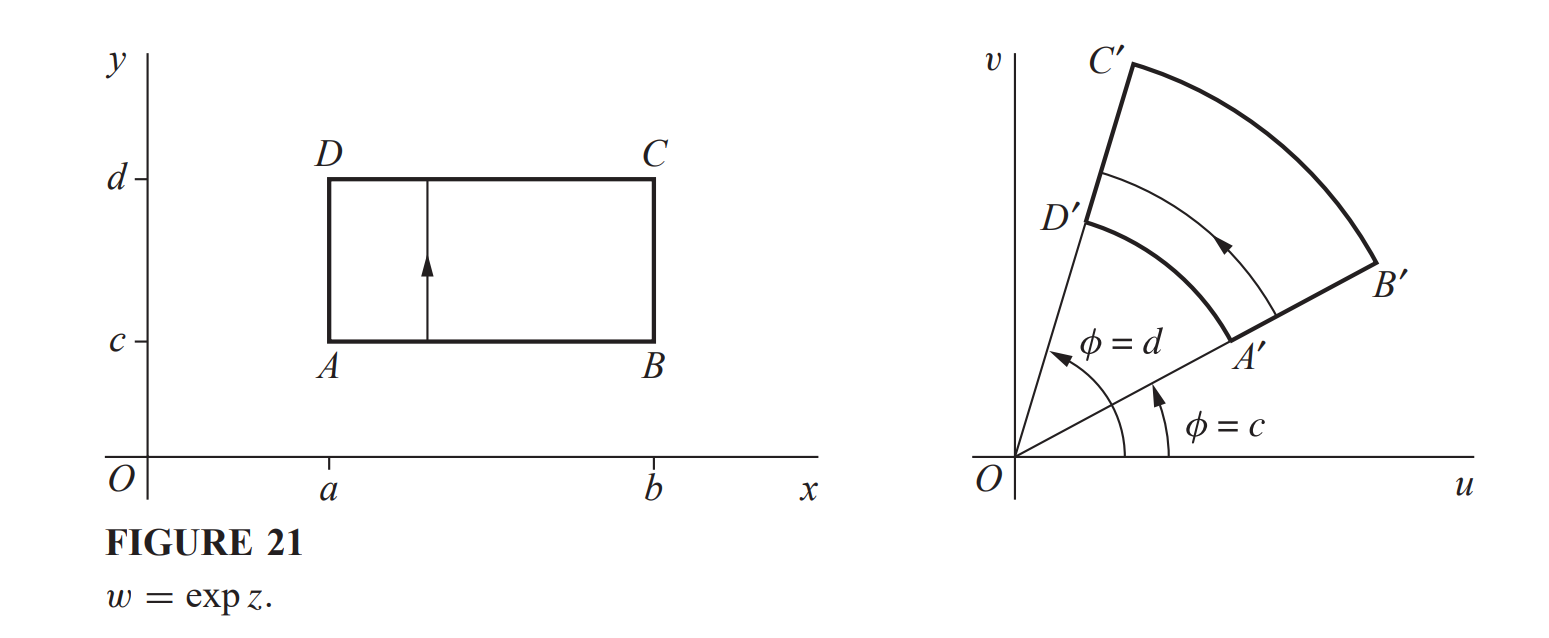
极限

函数极限

对于任意$\epsilon>0$都有$\delta>0$使得$0<|x-x_0|<\delta$有$|f(x)-A|<\epsilon$

类比

对于任意$\epsilon>0$都有$\delta>0$使得$0<|z-z_0|<\delta$有$|f(z)-w_0|<\epsilon$

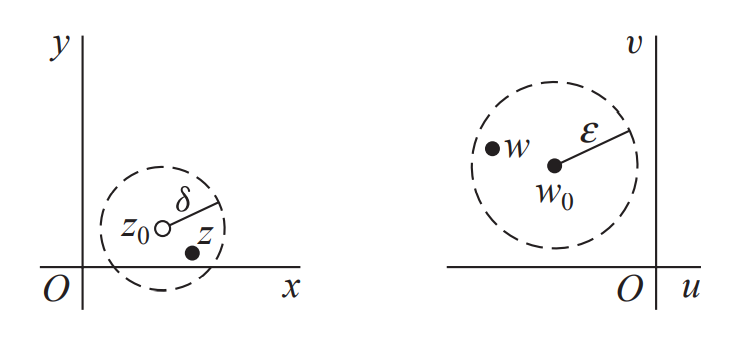
则记为

$\lim_{z\to z_00}f(z)=w_0$

定理

$\lim_{z\to z_0}f(z)=w_0\Leftrightarrow\begin{cases}\displaystyle\lim_{(x,y)\to(x_0,y_0)}u(x,y)=u_0\\ \displaystyle\lim_{(x,y)\to(x_0,y_0)}v(x,y)=v_0\end{cases}$

利用这个定理可以很方便地将复变函数的极限转换为一般函数极限

所以四则运算法则同一般函数极限的运算法则

没有所谓左右极限的概念

无穷

将无穷远点(point at infinity)引入复平面，得到扩充复平面

全体复数再加上一个无穷远点构成扩充复数

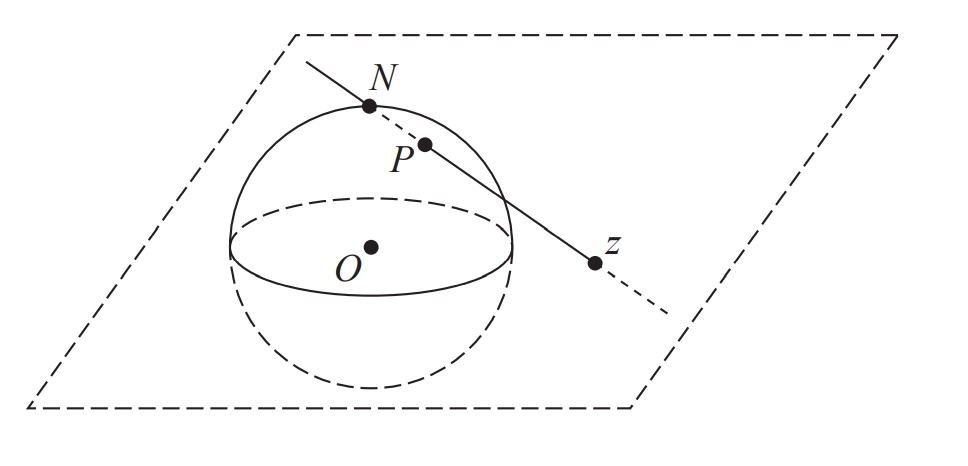
引入黎曼球面，球面投影点$z$为复平面上的点，和球面上的$P$一一对应

加上无穷远点$N$代表无穷远点，构成了球和复数的对应关系

可以通过倒数来将极限转化为0

$\lim_{z\to \infty}f(z)=\infty\Leftrightarrow \lim_{z\to 0}\frac1{f(1/z)}=0$

连续

定义为

$\displaystyle \lim_{z\to z_0}f(z)$存在
$f(z_0)$存在
$\displaystyle \lim_{z\to z_0}f(z)=f(z_0)$

同理有若两函数都连续则$f(g(x))$也连续

如果函数在某一封闭区域内连续那么

$|f(z)|\le M$

导数

$f'(z_0)=\lim_{\Delta z\to0}\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}$

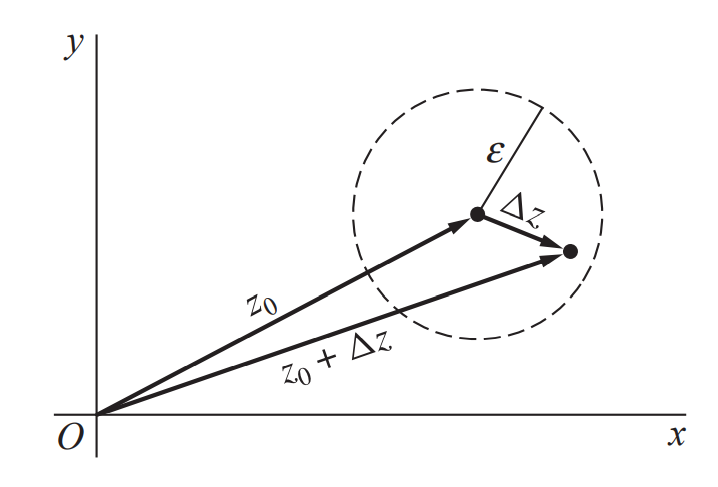
导数的大部分公式都可以用于复变函数，但复变函数自变量为二维，所以趋向有方向

但因为导数定义，不同趋向极限应该相同，得到可导的必要条件

$\begin{cases}\displaystyle\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\\ \displaystyle\frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}\end{cases}$

这就是柯西-黎曼方程(Cauchy–Riemann Equations)

$f'(z_0)=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\text{i}$

导数还可以用极坐标来表示

$\\f'(z)=f'(re^{\theta\text{i}})=u(r,\theta)+v(r,\theta)\text{i}$ $\begin{cases}ru_r=v_\theta\\ u_\theta=-rv_r\end{cases}\\ f'(z_0)=e^{-\theta\text{i}}(u_r+v_r\text i)$

解析函数

某区域上处处可微分的复变函数

If we should speak of a function $f$ that is analytic in a set $S$ which is not open, it is to be understood that $f$ is analytic in an open set containing $S$

如果$f’(z)=0$在$D$上恒成立则$f(z)$在$D$上是常函数

调和函数

有二阶导数同时满足拉普拉斯方程

$\frac{\partial^2 f}{\partial x_1^2}+\frac{\partial^2 f}{\partial x_2^2}+\cdots+\frac{\partial^2 f}{\partial x_n^2}=0$

对于复变函数，如果在$D$上是解析函数，则两个分量$u,v$是调和函数

特殊函数

指数函数$e^z$运算法则符合一般指数的运算

$\frac{\text{d}}{\text{d}z}e^z=e^z\\ e^{z+2n\pi\text{i}}=e^z$

对数函数

$\ln z=\ln r+\text{i}(\Theta+2n\pi)\\ \Theta=\text{Arg } z$

对应多个值，如果我们限定主枝(principal branch)

$\ln z=\ln r+\text i\Theta\quad(\Theta\in(-\pi,\pi))$

不能取等否则不连续，一般$\log z\Leftrightarrow\ln z$

$\log z_1z_2=\log z_1+\log z_2\\ \log \left (\frac{z_1}{z_2}\right )=\log z_1-\log z_2\\ z^n=e^{n\log z}$

$n$可以为复数，即指数为复数

三角函数

利用欧拉公式，利用共轭复数得到

$\sin z=\frac{e^{\text i z}-e^{-\text i z}}{2\text i}\\ \cos z =\frac{e^{\text i z}+e^{-\text i z}}{2\text i}$

许多性质和三角函数一模一样

$\frac{\text d} {\text dz }\sin z=\cos z\\ \sin(z_1 + z_2) = \sin z_1 \cos z_2 + \cos z_1 \sin z_2\\ \sin ^2z+\cos ^2z=1$

对于双曲函数

$\sinh z=\frac{e^z-e^{-z}}2\\ \cosh z=\frac{e^z+e^{-z}}2\\ \sin(\text iz)=\text i\sinh z\\ \cos(\text iz)=\sinh z$