大一/物理/电场

引入

远距作用

过去人们认为相距一段距离的物体发生相互作用是一种远距作用(action at a distance)

它不需要中间介质的传递只需要两个物体就能发生

但很多现象无法解释例如为什么有的时候只有直接接触才能产生力

场论

因此后来人们认为两个相距一段距离的物体之间存在一种物质通过连续的相互作用使作用得到传递，人们把它称之为场

作用在场中的传递就像力在弹簧中的传递一样

标量场

$$f(x,y,z)$$

空间中的每一个点都对应一个标量

固定一个分量可以使用等高线来表示

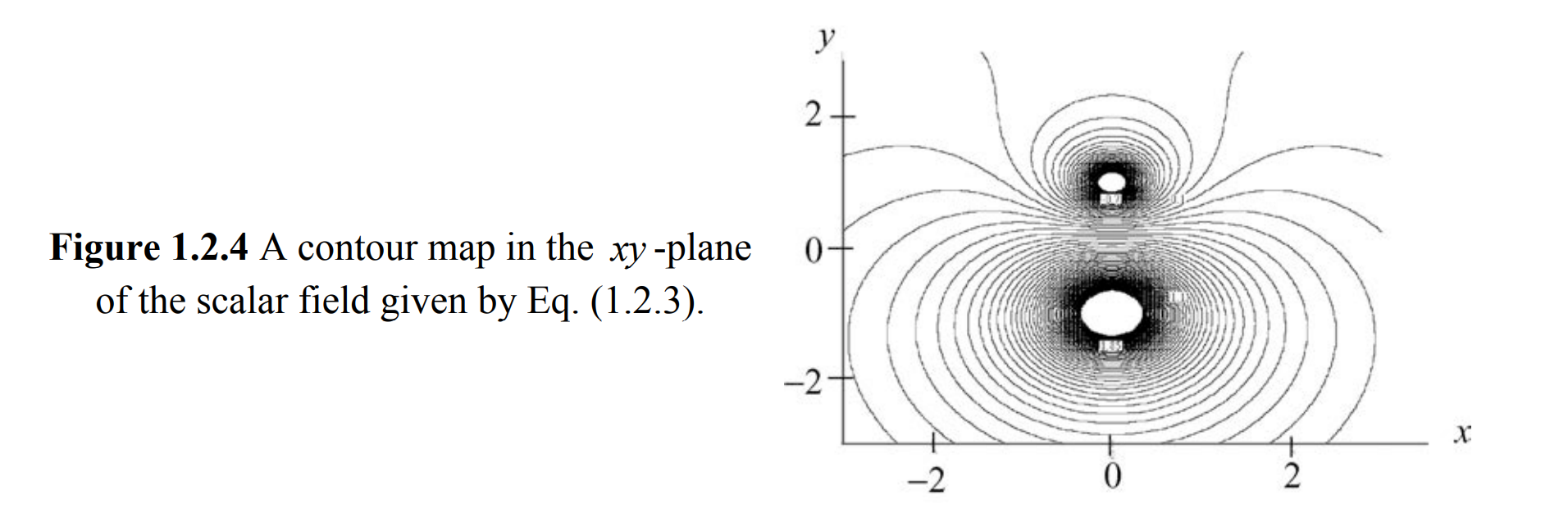
还可以使用颜色映射或三维地形图(Relief Maps)来表示

向量场

结果为向量

$$\vec{F}(x,y,z)=f_x(x,y,z)\mathbf{i}+f_y(x,y,z)\mathbf{j}+f_z(x,y,z)\mathbf{k}$$

流场

$$\overrightarrow{\mathbf{v}}(x, y, z)=v_{x}(x, y, z) \hat{\mathbf{i}}+v_{y}(x, y, z) \hat{\mathbf{j}}+v_{z}(x, y, z) \hat{\mathbf{k}}$$

电场中很多的概念是从流场中类比而来的

重力场

$$\vec{g}=-G\frac{M}{r^2}\hat{\mathbf{r}}$$

电场

由库仑定律得到

$$\vec{F}_e=k_e\frac{Qq}{r^2}\hat{\mathbf r},\vec{E}_e=k_e\frac{Q}{r^2}\hat{\mathbf r}\\ k_e=\frac1{4\pi\varepsilon _0}$$

注意电荷有正负

$$\vec{F}_e=q\vec{E}_e$$

对于场强，由微元法

$$\text d\vec{E}_e=k_e\frac{\text dQ}{r^2}\hat{\mathbf r}\\$$

积分

$$\vec{E}_e=k_e\int_V\frac{\text dQ}{r^2}\hat{\boldsymbol r}\\ \text dQ=\lambda\text{d}x= \sigma\text{d}S= \rho\text{d}V$$

磁场

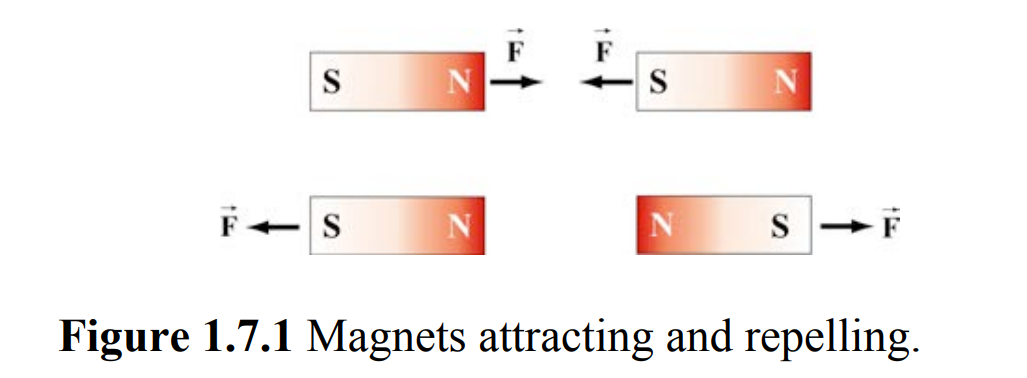
在周围放置许多小磁针，由于力矩的作用使得小磁针成如下排列

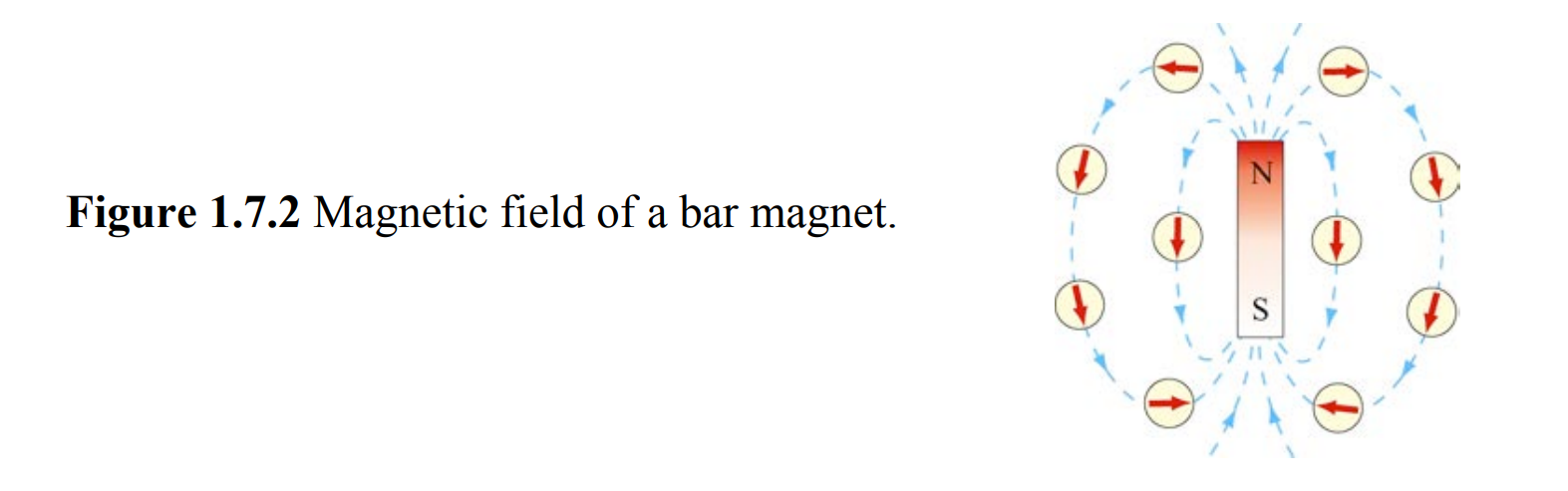
这形成的一根根线被法拉第描述成电场线

电场线的切线代表该点处的场强方向

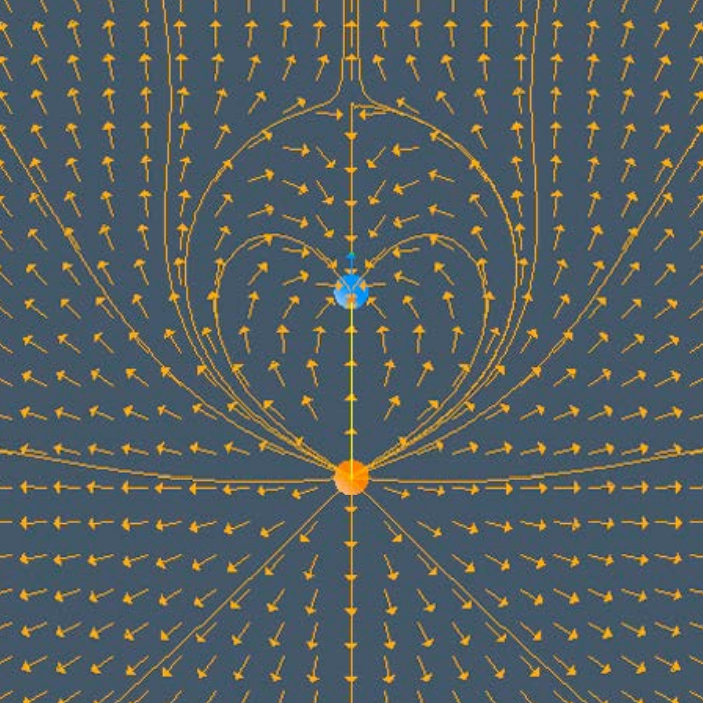
Faraday called the field lines for electric field “lines of force.”

运动的电荷产生磁场(电生磁)

高斯定理

电通量

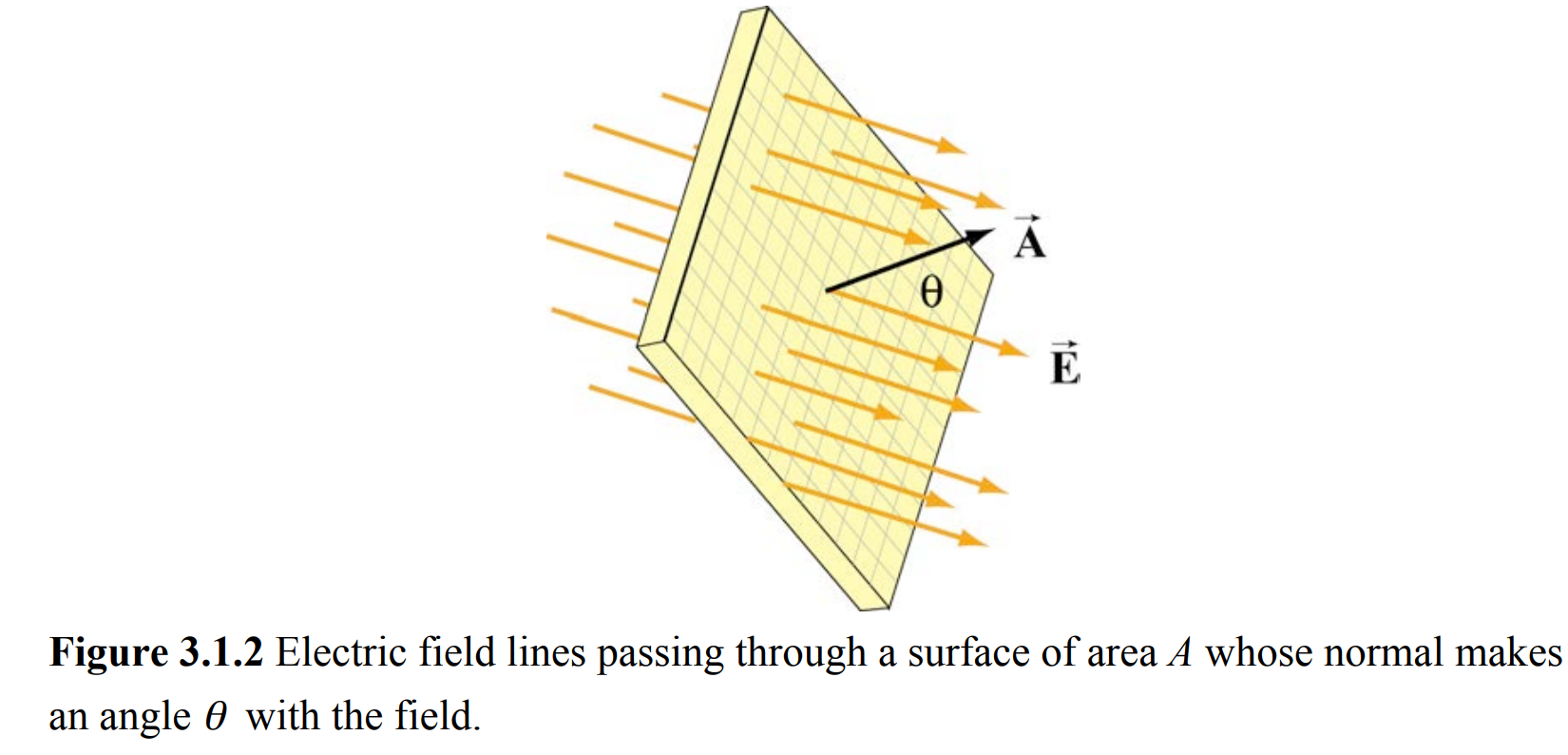
用电通量来描述穿过某一面积的电场线条数

$$\Phi=\vec E\cdot \vec S$$

利用点电荷的电通量公式可以导出

$$\Phi_e=\frac{q}{\varepsilon_0}$$

库仑力满足平方反比关系，故有高斯定理

$$\Phi=\oint_{S}\vec E\cdot \text d\vec S=\frac1{\varepsilon_0}\sum_{i=1}^nq_i$$

应用

如果选取恰当的高斯面(球面或柱面)，则

$$E,\cos \theta=\text{constant}$$

就可以通过电荷量计算出场强

无限长的导线

$$E=\frac\lambda{4\pi\varepsilon_0 r}(\cos\theta_1-\cos\theta_2)\\ E=\frac\lambda{2\pi\varepsilon_0 r}$$

无限大平板

$$E=\frac{\sigma}{2\varepsilon_0 }$$

对电偶极子，$p=ql$由负到正

$$E=\frac{-p}{4\pi\varepsilon_0r^3}$$

电势能

电场力为保守力，做功与路径无关

$$W_{ab}=\frac{q_0}{4\pi\varepsilon_0}\sum_iq_i\left(\frac1{r_{ia}}-\frac1{r_{ib}}\right)$$

所以有环路定理

$$\oint_lE\cdot\text dl=0$$

电场力对应一种势能

$$\Delta V_{e}=-\int_{A}^{B}\left(\overrightarrow{\mathbf{F}}_{e} / q_{t}\right) \cdot \text d \overrightarrow{\mathbf{s}}=-\int_{A}^{B} \overrightarrow{\mathbf{E}} \cdot \text d \overrightarrow{\mathbf{s}},\\ \Delta U=q_t\Delta V_e$$

故有保守力做功等于势能的减少量

$$\Delta U=-W_e\\ \Delta V = \Delta V_{CA} + \Delta V_{BC}$$

对于点电荷

$$\Delta E=E_{B}-E_{A}=-\int_{A}^{B} \frac{Q}{4 \pi \varepsilon_{0} r^{2}} \text d r=\frac{Q}{4 \pi \varepsilon_{0}}\left(\frac{1}{r_{B}}-\frac{1}{r_{A}}\right)$$

As in the case of gravity, only the difference in electrical potential is physically meaningful, and one may choose a reference point and set the potential there to be zero. In practice, it is often convenient to choose the reference point to be at infinity, so that the electric potential at a point P becomes

$$V_p=\int_p^\infty\overrightarrow{\mathbf{E}} \cdot \text d \overrightarrow{\mathbf{s}},\quad V_\infty=0\\ V = k_e\frac Q r$$

点乘，所以考虑梯度

$$E=-\nabla V=-\left(\frac{\partial V}{\partial x},\frac{\partial V}{\partial y},\frac{\partial V}{\partial z}\right)$$

更严谨的

$$\text dV=\frac{\partial V}{\partial x}\text dx+\frac{\partial V}{\partial y}\text dy+\frac{\partial V}{\partial z}\text dz\\ \text dV=-E\cdot \text d s$$

导体的电场

静电平衡

对于导体内部，条件为

$$E+E_{感}=0$$

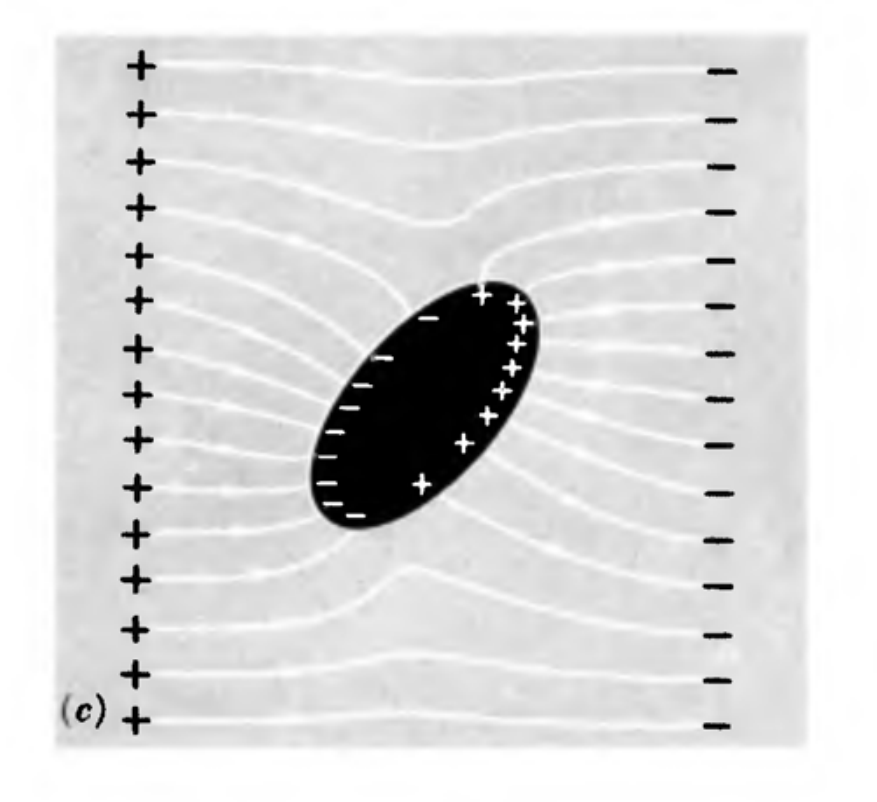
对表面用高斯定理得到若内部没有电荷则电荷只能在表面分布

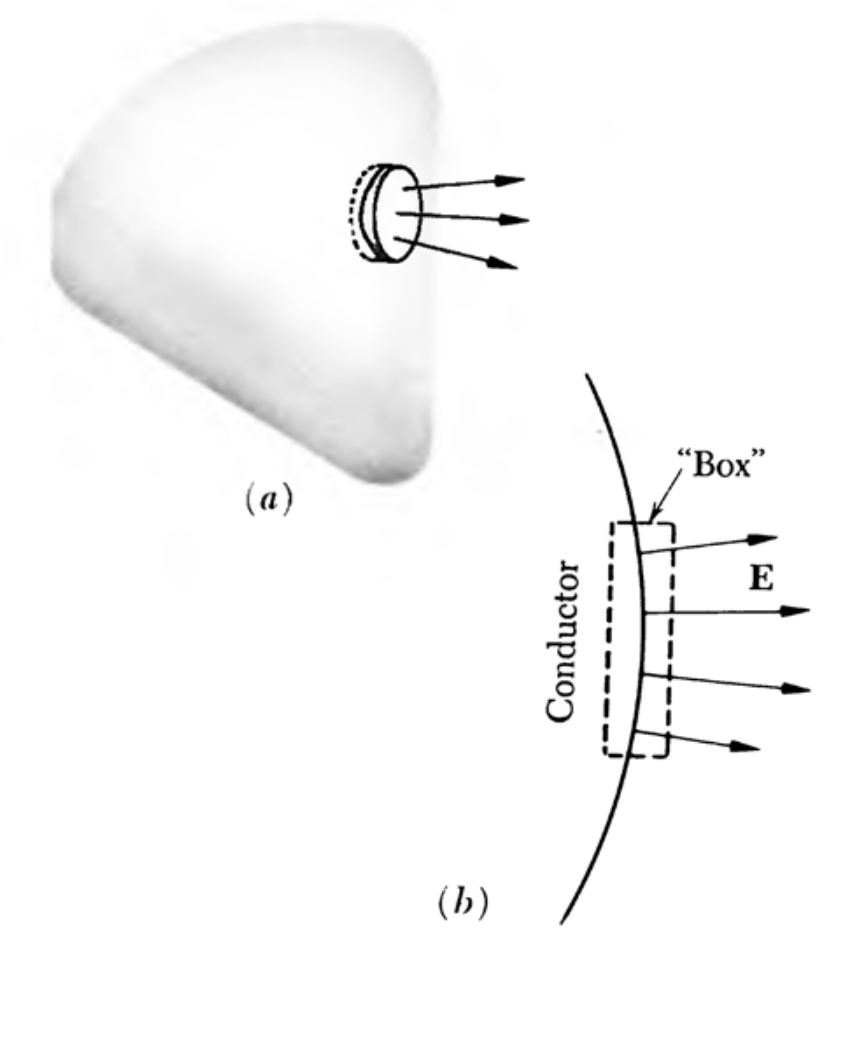
对于表面电场(区分于内部)

$$E=\frac \sigma{\varepsilon_0}$$

对于内部有电荷的情况，内外不会相互影响

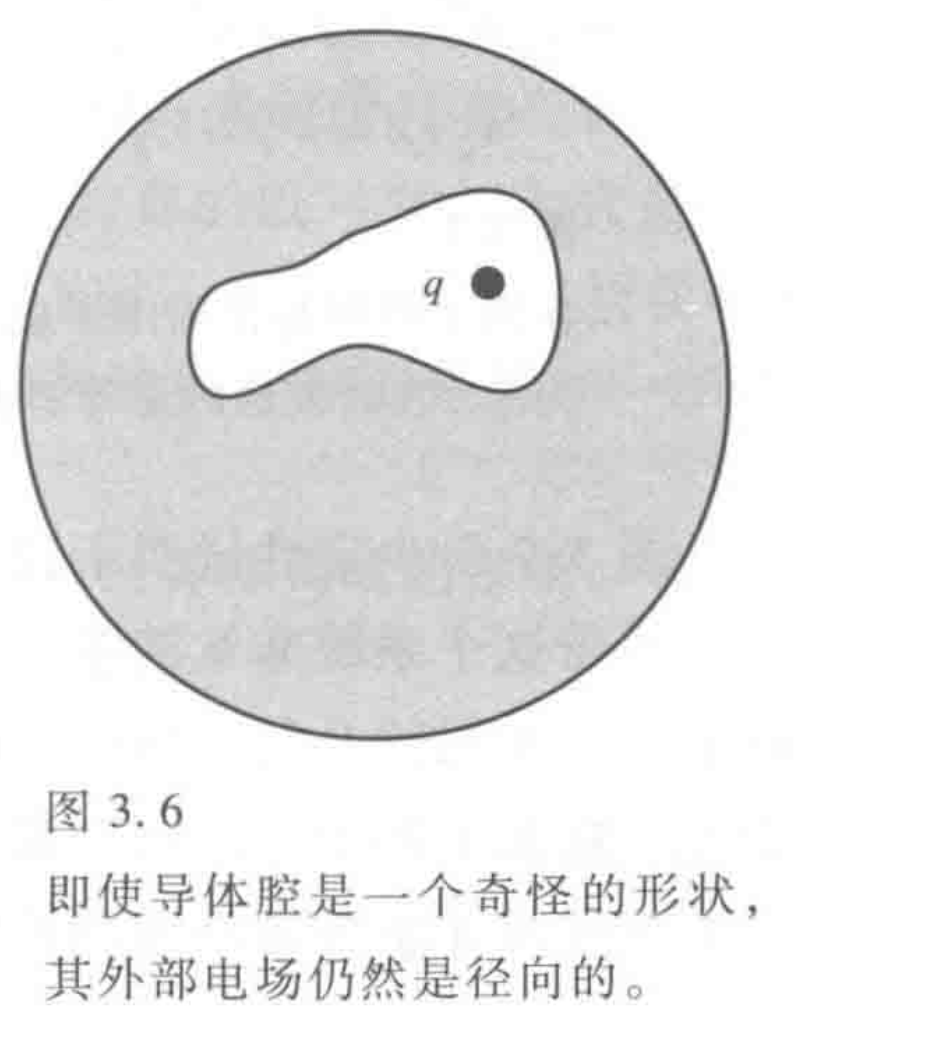
内部电荷为$-q$，外层分布只和外电场有关

若接地则为静电屏蔽，没有电场

电介质

因为电介质常为中性存在正负电荷所以引入电偶极子和偶极矩(电矩)

$$\vec p=q\vec l$$

方向由负电荷指向正电荷

电介质中存在大量电偶极子，所以引入电极化强度

$$\boldsymbol P=\frac{ \sum_i\boldsymbol p_i }V$$

对于表面，有

$$\sigma'=P\cos\theta =P_n$$

高斯定理

单独对极化电荷

$$\oint_{S}\vec P\cdot \text d\vec S=-\sum_{i}q_{i}$$

为了方便计算单独考虑自由电荷产生的电场

$$\oint_{S}(\varepsilon_0E+P)\cdot \text d\vec S=-\sum_{\text{free}}q_{i}$$

从而定义电位移

$$D=\varepsilon_0E+P\\ E=\frac{D-P}{\varepsilon_0}$$

合场强是由自由电荷和极化电荷产生电场的叠加

类比电场线我们可以引入电位移线，始于正自由电荷终于负自由电荷

对于各向同性的电介质，$\chi _e$为电极化率

$$P=\chi _e\varepsilon_0E\\ D=(1+\chi _e)\varepsilon_0E=\varepsilon_r\varepsilon_0E=\varepsilon E$$

将$\varepsilon$称为为电介质的介电常量，$\varepsilon_r$为相对介电常量

电容器

电容为电容器容纳电荷的本领

$$C=\frac{Q}V$$

单位为法拉

$$\rm 1 F=10^6\mu F=10^{12}pF$$

常见电容器

平行板电容器

$$C=\frac{\varepsilon_r\varepsilon_0S}{d}$$

将$\varepsilon$称为为电容率，$\varepsilon_r$为相对电容率

球型

$$C=\frac{4\pi \varepsilon R_A R_B}{ R_B-R_A}$$

圆柱

$$C=\frac{2\pi\varepsilon l}{\ln\frac{R_B}{R_A}}$$

连接

和电阻相反

串联

$$\frac1C=\sum_i\frac1{C_i}$$

并联

$$C=\sum_i C_i$$

静电场的能量

电荷之间相互作用从而存在能量，类比引力势能

$$W_e=\frac12\sum_iq_iV_i$$

对于连续分布的带电体

$$W_e=\frac12\int_qV\text dq$$

电容器

由于电容器的$U$为电势差，充电时电荷从一个极板移向另一个极板

$$W=\frac12QU=\frac 12CU^2=\frac12\frac{Q^2}C$$

所以从广义上讲，电场的能量就是聚集电荷所需的功

$$W_e=\int _V\frac 12\varepsilon E^2\text dV$$

其中$\frac 12\varepsilon E^2$为电场的能量密度