傅里叶变换

$g(t)-A_0=\sum_{i=0}^\infty A_n\cos(n\omega t+\varphi_n)$

考虑这个图形的质心

$g(t)e^{-2\pi ft \text{i}}\\ z_c=\frac1N\sum_{k=0}^{N-1}g(t_k)e^{-2\pi ft_k \text{i}}$

取极限，并不需平均

$\hat{g}(f)=\int_{0}^{t_m}g(t)e^{-2\pi ft \text{i}}\text{d}t$

利用复数的三角形式

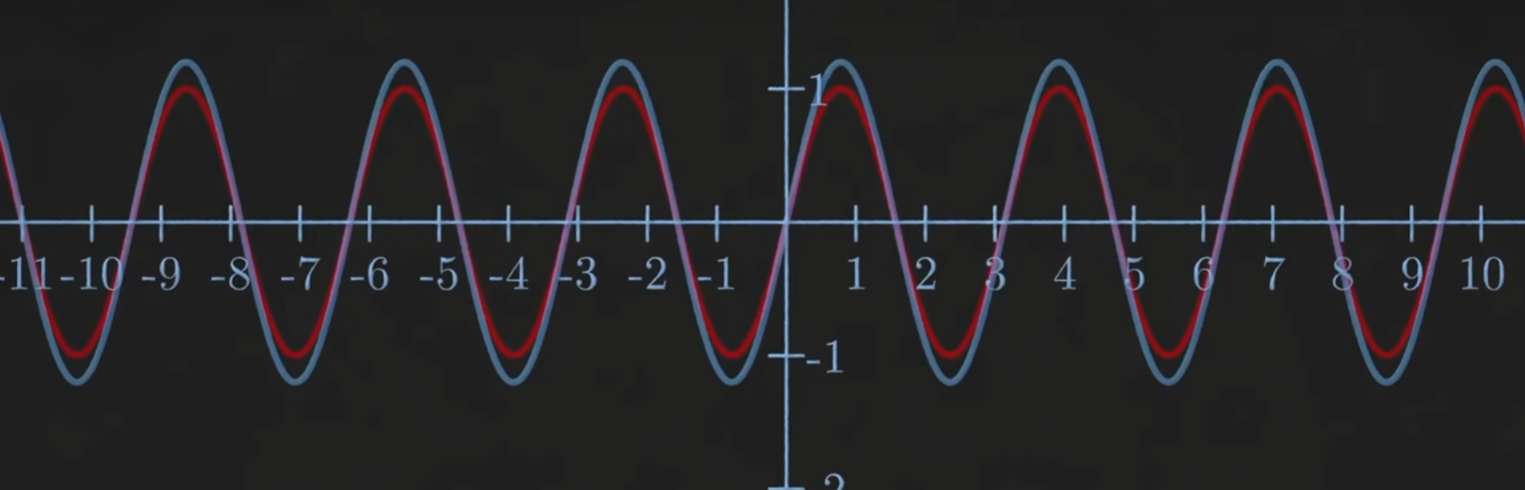
当频率匹配时，积分为正

由三角函数的正交性，若正交，为零

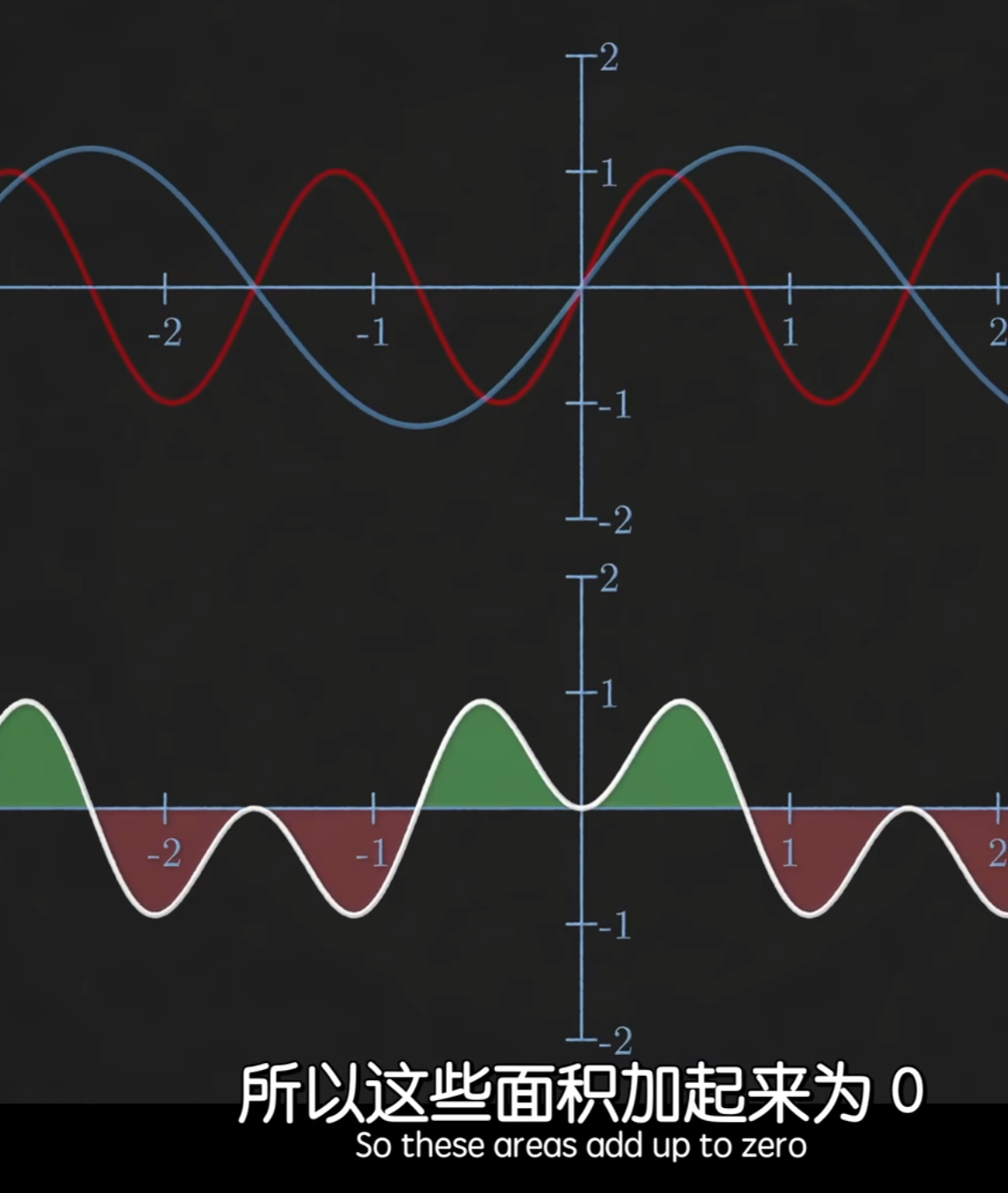
从而得到两个分量$\sin | \cos$的强度

快速傅里叶变换

多项式乘法

对于多项式

$A(x)=\sum_{i=0}^{n-1}a_ix^{i}\\ B(x)=\sum_{i=0}^{n-1}b_ix^{i}\\ C(x)=A(x)B(x)=\sum_{i=0}^{2n-2}c_ix^{i}\\ c_i=\sum_{j=0}^ia_jb_{i-j}$

这是多项式的系数表示，但还可以使用点值表示

$\{(x_0,y_0),(x_1,y_1)\dots(x_{n-1},y_{n-1})\}$

其中$x_i$各不相同，可以证明两种表示是等价的

$\left[\begin{array}{c} P\left(x_{0}\right) \\ P\left(x_{1}\right) \\ \vdots \\ P\left(x_{n-1}\right) \end{array}\right]=\left[\begin{array}{ccccc} 1 & x_{0} & x_{0}^{2} & \cdots & x_{0}^{n-1} \\ 1 & x_{1} & x_{1}^{2} & \cdots & x_{1}^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^{2} & \cdots & x_{n-1}^{n-1} \end{array}\right]\left[\begin{array}{c} p_{0} \\ p_{1} \\ \vdots \\ p_{n-1} \end{array}\right]$

所以$C(x)$可以表达为

$\{(x_0,y_0y_0'),(x_1,y_1y_1')\dots(x_{2n-2},y_{2n-2}y_{2n-2}')\}$

利用拉格朗日插值公式

$A(x)=\sum_{k=0}^{n-1}y_k\frac{\displaystyle\prod_{j\ne k}(x-x_j)}{\displaystyle\prod_{j\ne k}(x_k-x_j)}$

可以快速将点值表示转化为系数表示

注意到$2n-2$为偶数，使用几何意义去理解

消去引理

$\omega_{dn}^{dk}=\omega_{n}^{k}\\ \omega_n^{\frac n2}=\omega^\frac12=\omega_2^1=-1$

折半引理

$(\omega_n^k)^2=\omega_\frac n2^k\\ (\omega_n^k)^2=(\omega_n^{k+\frac n2})^2\;\;2\theta/2(\theta+\pi)$

求和引理

对于$\forall n\ge1,n\mod k\ne0$

$\sum_{j=0}^{n-1}(\omega_n^k)^j=0$

利用$n$次单位根，带入可以得到

$y_k=\sum_{j=0}^{n-1}a_j(\omega_n^k)^j$

从而向量

$(y_0,y_1,\cdots ,y_{n-1})$

为系数向量的离散傅里叶变换(DFT)

FFT

$A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)$

从而对$k:0\to \frac n 2-1$有

$\begin{cases}y_k=y^{[0]}_k+\omega_n^ky_k^{[1]}\\ y_{k+n/2}=y^{[0]}_k-\omega_n^ky_k^{[1]}\end{cases}$

从而分为两个规模为一半的子问题

$\left[\begin{array}{c} P\left(\omega^{0}\right) \\ P\left(\omega^{1}\right) \\ P\left(\omega^{2}\right) \\ \vdots \\ P\left(\omega^{n-1}\right) \end{array}\right]=\left[\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^{2} & \cdots & \omega^{n-1} \\ 1 & \omega^{2} & \omega^{4} & \cdots & \omega^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{n-1} & \omega^{2(n-1)} & \cdots & \omega^{(n-1)(n-1)} \end{array}\right]\left[\begin{array}{c} p_{0} \\ p_{1} \\ p_{2} \\ \vdots \\ p_{n-1} \end{array}\right]$ $\left[\begin{array}{c} p_{0} \\ p_{1} \\ p_{2} \\ \vdots \\ p_{n-1} \end{array}\right]=\frac{1}{n}\left[\begin{array}{ccccc} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega^{-1} & \omega^{-2} & \cdots & \omega^{-(n-1)} \\ 1 & \omega^{-2} & \omega^{-4} & \cdots & \omega^{-2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{-(n-1)} & \omega^{-2(n-1)} & \cdots & \omega^{-(n-1)(n-1)} \end{array}\right]\left[\begin{array}{c} P\left(\omega^{0}\right) \\ P\left(\omega^{1}\right) \\ P\left(\omega^{2}\right) \\ \vdots \\ P\left(\omega^{n-1}\right) \end{array}\right]$

而离散傅里叶变换可以写为

$z_c=\sum_{k=0}^{N-1}g(t_k)e^{-2\pi ft_k \text{i}}$

这就是带入单位根后的多项式的形式

化简

$z_c=\sum_{k=0}^{N-1}x_ke^{-2\pi f_rt_k \text{i}}\\$

总共有N个频率$f_r(0\le r\le n-1)$，让其等距分布

$\\-2\pi f_rt_k=-2\pi f_r\frac{k}{f_s}$

等距，所以令

$\frac{f_r}{rf_s}=\frac1{N}$

得

$X_r=\sum_{k=0}^{N-1}x_ke^{-(2\pi/N) rk\text{i}}$

结果

采样定理告诉我们，采样频率要大于信号频率的两倍

时域到频域，将N个采样点变为N个复数

$t\to f\\ A\to z$

设采样频率为$f_s$，则FFT的分辨率为$f_s/N$

$f_i=\frac{(i-1)f_s}N$

$z$的模长反映了振幅占比

$A_i=\frac{2||z_i||}{N}$

每个分量的相位为对应复数的相位

$\tan \varphi=\frac{\Im z}{\Re z}$

由于$Xr$和$X{N-r}$共轭，取模后相等

所以FFT的结果左右是对称的，只需取一般