大一/数据科学/回归

回归模型

输入向量

$$X=\begin{pmatrix}X_1\\X_2\\X_3\end{pmatrix}\\$$

模型

$$Y=f(X)+\epsilon$$

其中$\epsilon$为误差，不可避免

回归函数(regression function)为理想目标

$$f(x)=E(Y|X=x)$$

$X$表示抽象特征$x$为具体值

需要准确根据所有数据选取模型的复杂度

线性模型

$$\hat { y } = \hat { \beta_1 } x + \hat { \beta_0}$$

几乎不可能正确，但很可能是最佳的一部分

$$\\ \frac{\partial y}{\partial \beta_1}=\frac{\partial y}{\partial \beta_0}=0\\ \hat { \beta_1 } = \frac { \sum\limits _ { i = 1 } ^ { n } x _ { i } y _ { i } - n \overline { x } \overline { y } } { \sum \limits_ { i = 1 } ^ { n } x _ { i } ^ { 2 } - n \overline { x } ^ { 2 } } , \hat { \beta_0 } = \overline { y } - \hat { b } \overline { x }$$

相关系数为

$$r = \frac { \sum \limits_ { i = 1 } ^ { n } x _ { i } y _ { i } - n \overline { x } \overline { y } } { \sqrt { ( \sum \limits_ { i = 1 } ^ { n } x _ { i } ^ { 2 } - n \overline { x } ^ { 2 } ) ( \sum \limits_ { i = 1 } ^ { n } y _ { i } ^ { 2 } - n \overline { y } ^ { 2 } ) } }$$

计算标准差的平方(方差)为

$$S_{xx}=\sum_{i=1}^n(x_i-\overline{x})^2\\ S_{yy}=\sum_{i=1}^n(y_i-\overline{y})^2\\ S_{xy}=\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})$$

标准差为

$$\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\hat{x}_{j}\right)^{2}}$$

其中$\sigma^2=\text{Var}(\epsilon)$

因为$x_i$为人为给定量，$y_i$为测量值，存在误差

若样本无穷大，有总体回归线

$$Y=\beta_0+\beta_1X+\epsilon$$

由方差的性质得到

$$\text{Var}(\epsilon)=\text{Var}[Y]$$

SE(Standard Error)为标准误差

1、均方差就是标准差，标准差就是均方差

2、方差 是各数据偏离平均值 差值的平方和 的平均数

3、均方误差（MSE）是各数据偏离真实值 差值的平方和 的平均数

4、方差是平均值，均方误差是真实值

RSE：Residual Standard Error

$$\mathrm{RSE}=\sqrt{\frac{1}{n-2} \operatorname{RSS}}=\sqrt{\frac{1}{n-2} \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{j}\right)^{2}}$$

RSS：Residual Sum of Squares

由误差导致的真实值和估计值之间的偏差平方和

置信区间

Confidence Intervals

有$95\%$的概率使得最佳值在区间内(根据数据的不同)

$$[\hat{\beta_1}-2\text{SE}(\hat{\beta_1}),\hat{\beta_1}+2\text{SE}(\hat{\beta_1})]$$

多元

$$f_L(X)=\beta_0+\beta_1X_1+\beta_2X_2\dots\\ Y=X\beta+\epsilon$$

若一个量变化，其余量固定不变，不相关(常常不符合事实)

但有一些很有用，能够看出某个量的影响

$$\text{minimize}\{\ell(\beta)= (Y-X\beta)^2\}\\ \frac{\partial l}{\partial \beta}=0,\ell(\beta)=(Y-X\beta)^T(Y-X\beta)$$

展开后求导可得

$$\beta=(X^TX)^{-1}X^TY$$

其中$X$代表$n$个样本

$$X=\begin{bmatrix}1&X_{11}&\cdots&X_{1(m-1)}&X_{1m}\\ 1&X_{21}&\cdots&X_{2(m-1)}&X_{2m}\\ 1&X_{31}&\cdots&X_{3(m-1)}&X_{3m}\\ \vdots& \vdots&\vdots&\vdots&\vdots\\ 1&X_{n1}&\cdots&X_{n(m-1)}&X_{nm}\\ \end{bmatrix}$$

对于

$$y=2x_1-3.4x_2+4.2\\ \beta=\begin{bmatrix}\beta_0\\\beta_1\\\beta_2\\ \end{bmatrix}$$

相关

若两个量相关则

$$\beta_1\ne0$$ $$\beta_1=0\Rightarrow Y=\beta_0+\epsilon$$

对于多元模型，可以引入乘积项

$$y=\beta_0+\beta_1X_1+\beta_2X_2+\beta_3X_1X_2+\epsilon$$

优化

最小化方差

$$\text{minimize}\{E[(Y-\hat{f}(x))^2|X=x]\}$$

$\hat{f}(x)$为所估计的函数

$$E[(Y-\hat{f}(x))^2|X=x]=[f(x)-\hat{f}(x)]^2+\text{Var}(\epsilon)$$

但每个值不一定都有

$$\rm good /over/under\;fitting$$

取测试数据集计算准确度，评估模型好坏

可以引入非线性项来改进模型

$$Y=\beta_0+\beta_1X+\beta_2X^2+\epsilon$$

分类模型

$$\hat{f}(x)=\text{Ave}(Y|X\in \mathcal{N}(x))$$

考察$x$的邻域$\mathcal{N}(x)$，如扩展到$10\%$的数据

但对高维数据范围太大失去了局部信息，效果不好

分类器$C(X)$，考虑条件概率

$$p_k(x)=\text{Pr}(Y=k|X=x),k=1,2,\dots ,k$$

分类结果为

$$Y=j \;\text{if}\;p_j(x)=\max\{p_k(x) \}$$

用正确率来衡量结果

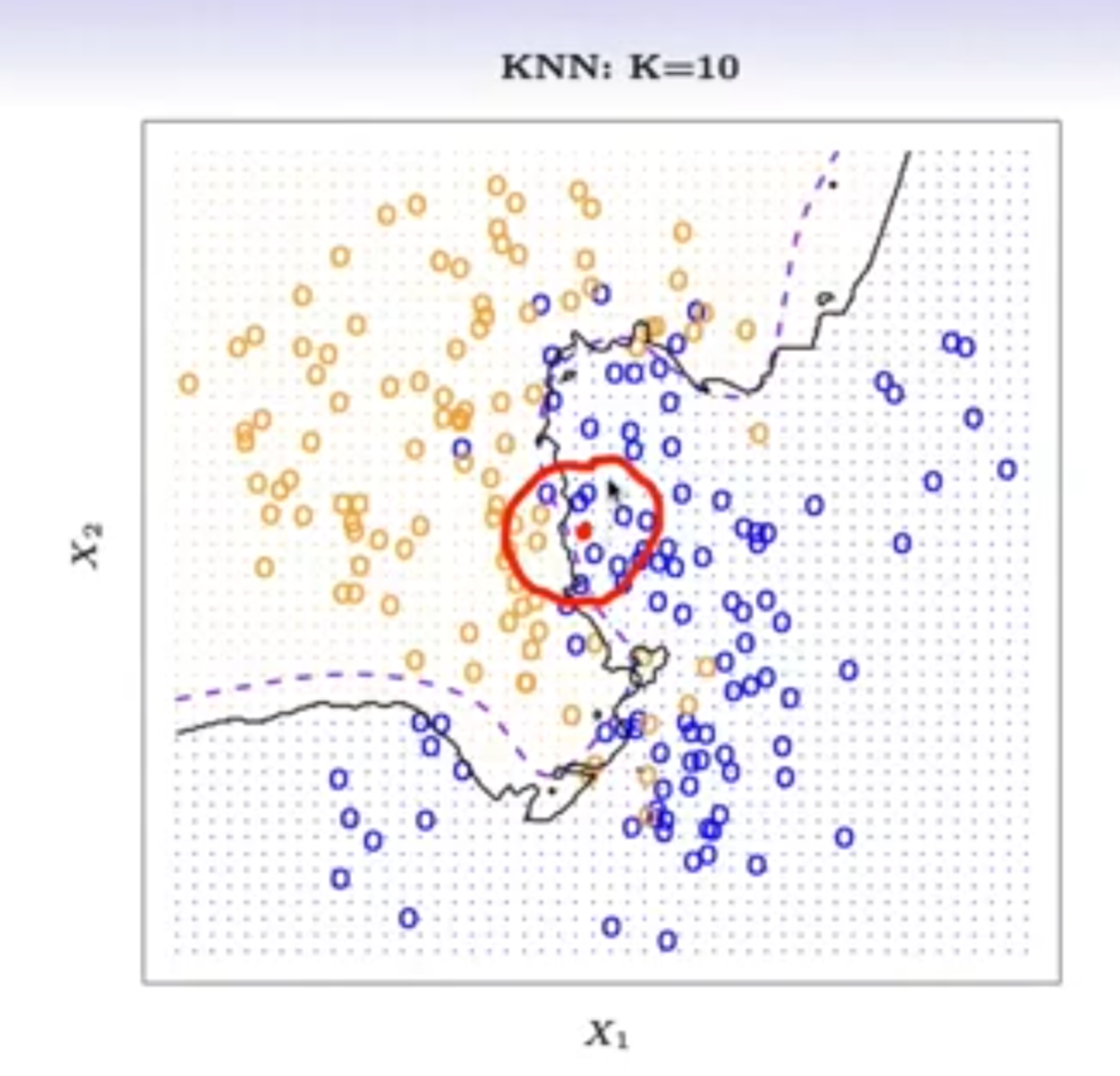
可使用$\rm Nearest-neighbor$，如找十个看哪种最多

Logistic

逻辑斯谛回归

$$p(X)=\text{Pr}\{Y=1|X\}\\ p(X)=\frac{e^{\beta_0+\beta_1X}}{1+e^{\beta_0+\beta_1X}}\\ \text{Pr}\{Y=0|X\}=\frac{1}{1+e^{\beta_0+\beta_1X}}\\ \ln \left(\frac{p(X)}{1-p(X)}\right)=\beta_{0}+\beta_{1} X\\$$

这是一种广义线性模型，利用最大似然函数估计误差

$$\ell\left(\beta_{0}, \beta\right)=\prod_{i: y_{i}=1} p\left(x_{i}\right) \prod_{i: y_{i}=0}\left(1-p\left(x_{i}\right)\right)$$

随机抽小球，取得一个样本

我们认为概率最大的情况就是这个结果，从而

$$\text{maximize}\{\ell\left(\beta_{0}, \beta\right)\}$$