大一/物理/热学

概念

系统

热力学系统由大量微观粒子组成的系统，与系统发生相互作用的外部环境称为外界

• 孤立系统：与外界没有物质和能量的交换
• 封闭系统：没有物质的交换，只有能量交换
• 开放系统：同时有物质和能量的交换

状态参量

分为宏观量和微观量

每个分子所具有的$v,m_p$为微观量

气体的宏观状态如$V,p$为宏观量

其中又分为广延量和强度量，如热量是广延量，温度是强度量

重要单位

$$1 \rm L=10^{-3}m^3\\ 1atm=1.013\times10^5Pa=760mmHg$$

热平衡

两者之间没有热量的交换，冷热程度不发生改变

平衡态

在经过足够长的时间后系统的状态参量不随时间改变，则称该系统达到了平衡态

弛豫时间

从初始状态到达到平衡态所需要的时间

若弛豫时间很短则可近似看作平衡态

准静态过程

过程足够缓慢以至于每一个中间态都可以看作平衡态

温标

温度的数值表示法

摄氏温标，用$t$表示，单位为$^\circ \text{C}$

热力学温标，用$T$表示，开尔文温标，单位为$\text{K}$

$$T/\text{K}=273.15+t/^\circ\text{C}$$

热力学定律

第零定律

若两个系统分别与第三个系统处于热平衡，则这两个系统必然也处于热平衡

第一定律

只要初末两个状态为平衡态

$$E=f(T) \\\Delta E= \Delta U=W+Q$$

实际上对系统做功和传递热量是等效的，焦耳实验测出了热功当量

我们需要注意做功和传热是过程量和具体过程有关

内能的变化量是状态量只和始末状态有关（处于平衡态）

$$J=\frac{2mgh}Q=4.18\text{J}\cdot\text{cal}^{-1}$$

对于微小过程(准静态)，有

$$\text{d}E=\text{d}W+\text{d}Q\\ \Delta E=-\int_{V_1}^{V_2}{p\text{d}V}+\int_{T_1}^{T_2}\frac mMC_m\text{d}T$$

闭口系统

上面的功定义为气体对外做的膨胀功$W$，则

$$Q=W+\Delta U\\ \delta Q=\delta U+\delta W$$

用比表示也即

$$q=\Delta u+w\\ \delta q=\delta u+\delta w$$

上面的式子适用于一切过程，不受过程性质和工质性质限制

对于可逆过程，上面有

$$q=\Delta u +\int_1^2p\text dv\\ \delta q=\delta u +p\delta v$$

开口系统

对于稳定流动，维持需要流动功和推动功

$$\delta W_f=pA\text d x=p\text d V=pv\text d m\\ w_f=pv$$

流动功不是工质本身的能量

所以对于开口系统，定义焓

$$\Delta H =\Delta U +p\Delta V$$

和工质通过机轴对外输出的功$W_s$，和流速$c_f$，根据能量守恒

$$Q=\Delta H+\frac12m\Delta c_f^2+mg\Delta z+W_s$$

单位工质

$$q=\Delta h+\frac12m\Delta c_f^2+g\Delta z+ w_s$$

技术功（工程上可以直接利用的功）

$$w_t=\frac12m\Delta c_f^2+g\Delta z+ w_s$$

再进行变形，定义膨胀功$w$

$$w_t=w-(p_2v_2-p_1v_1)$$

技术功等于膨胀功减去净流动功

对于可逆过程，可以把技术功表示为

$$w_t=-\int_1^2v\text dp$$

为与$p$轴围成的面积

理想气体

热容

可以看出热容的定义为

$$C=\frac{\delta Q}{\delta t}$$

上面换成比热得到比热容

$$c=\frac{\delta q}{\delta t}$$

其中$C_m=cM$为摩尔热容，对于特殊过程，引入自由度

• $i=3$单原子分子
• $i=5$双原子分子
• $i=6$多原子分子

从而有定压热容和定容热容

$$V=\text{const}:\\ C_{V,m}=\frac i2R \\ p=\text{const}:\\ C_{p,m}=\left(\frac i2+1\right)R$$

从而有迈耶公式

$$C_{V,m}+R=C_{p,m}$$

$R$在数值上等于一摩尔理想气体等压过程升高$1\text{K}$对外做的功（克服外力膨胀）

定义比热容比

$$\gamma=c_p/c_v>1$$

带入上面的关系得到

$$c_p=\frac\gamma{\gamma-1}R_g\\c_v=\frac1{\gamma-1}R_g$$

从定容推出的内能表达式适用于所有过程

$$E=\frac mMC_{V,m}T=\frac mM\frac i2RT$$

物态方程

$$\frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}$$

标准状态

$$p_0=1 \text{atm},T_0=273.15\text{K},V_m=22.4\text{L/mol}$$ $$\frac{p_1V_1}{T_1}=\frac mM \frac{p_0V_m}{T_0}=R\frac mM$$ $$pV=\frac mM RT$$

这就是理想气体状态方程，$R=8.31$为摩尔气体常量

对方程进行变化，令

$$\frac{R}{M}=R_g$$

则得到了气体常数（只和气体种类有关，和状态无关）

再用比体积（单位质量）替代体积，得到

$$pv=R_gT$$

称为理想气体状态方程式（克拉贝龙方程式）

$$p=\frac NV\frac R{N_A}T=nkT$$

其中$k=R/N_A$称为玻尔兹曼常量，此式多用于计算分子数密度

带入标况可得

$$n=2.69\times{10}^{25}\rm m^{-3}$$

这个量被称为洛施密特常量

热力学过程

等体过程

$$Q_V=\Delta E=\frac mM\frac i2R\Delta T$$

等压过程

$$\Delta E=p(V_1-V_2)+\frac mM\left(\frac i2+1\right)R\Delta T$$

等温过程

$$p_1V_1=p_2V_2\\ W=\frac mMRT\ln\frac{V_1}{V_2}=\frac mMRT\ln\frac{p_2}{p_1}=Q_T$$

其中摩尔定温热容

$$C_{T,m}=\frac Mm\left(\frac{\text{d}Q}{\text{d}T}\right)_T\to\infty$$

绝热过程

$$\Delta E=W,\text{d}E=\frac mMC_V\text{d}T\\ \text{d}W=-p\text{d}V$$

引入绝热指数(摩尔热容比)

$$\gamma=\frac{C_{p,m}}{C_{V,m}}=\frac{i+2}i$$

得到绝热方程

$$pV^{\gamma}=C_1\\ TV^{\gamma-1}=C_2\\ \frac{T^{\gamma}}{p^{\gamma-1}}=C_3$$ $$W=\frac1{\gamma-1}(p_2V_2-p_1V_1)=C_V(T_2-T_1)$$

在交点处，绝热过程的线更加陡

多方过程

$$pV^n=C$$

做功把绝热过程中的$\gamma\to n$即可，注意

$$C_{n,m}=C_{V,m}+\frac R{1-n}$$

循环过程

某个状态出发经过一系列过程又回到初始状态的过程

顺时针为正，逆时针为负

正循环$W’>0$，逆循环相反

热机

吸热为$Q_1$，放热为$Q_2$

$$\eta=\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}=1-\frac{Q_2}{Q_1}$$

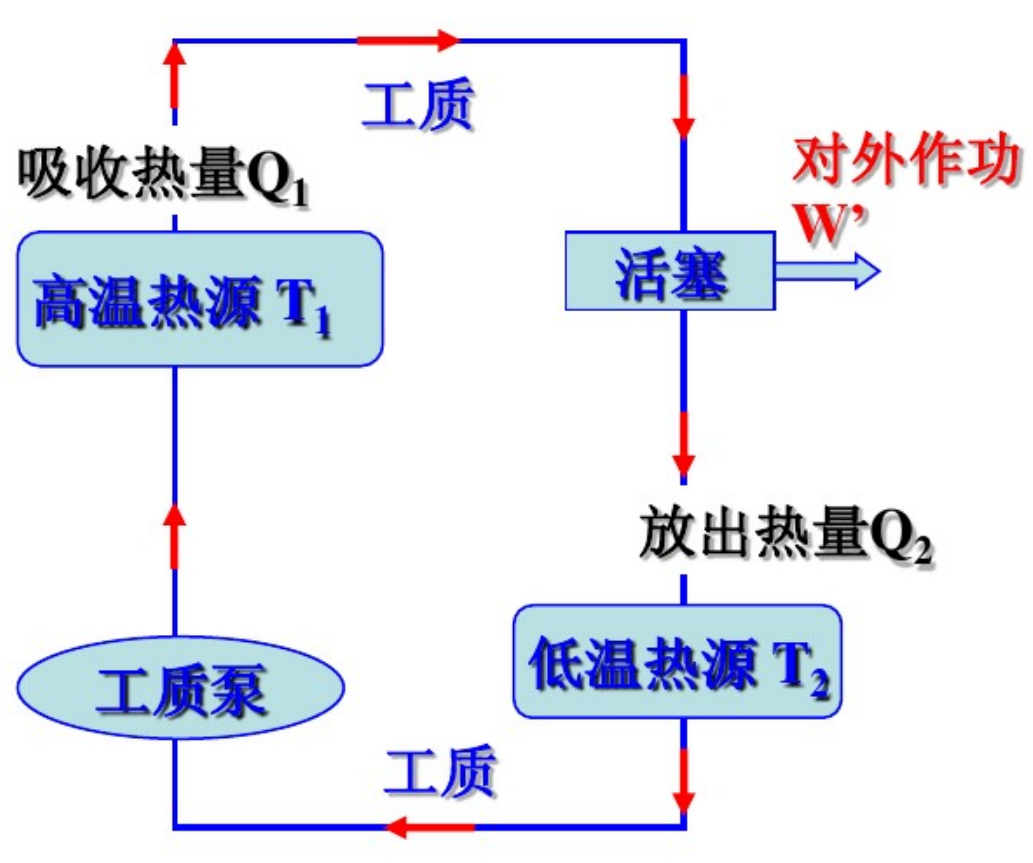
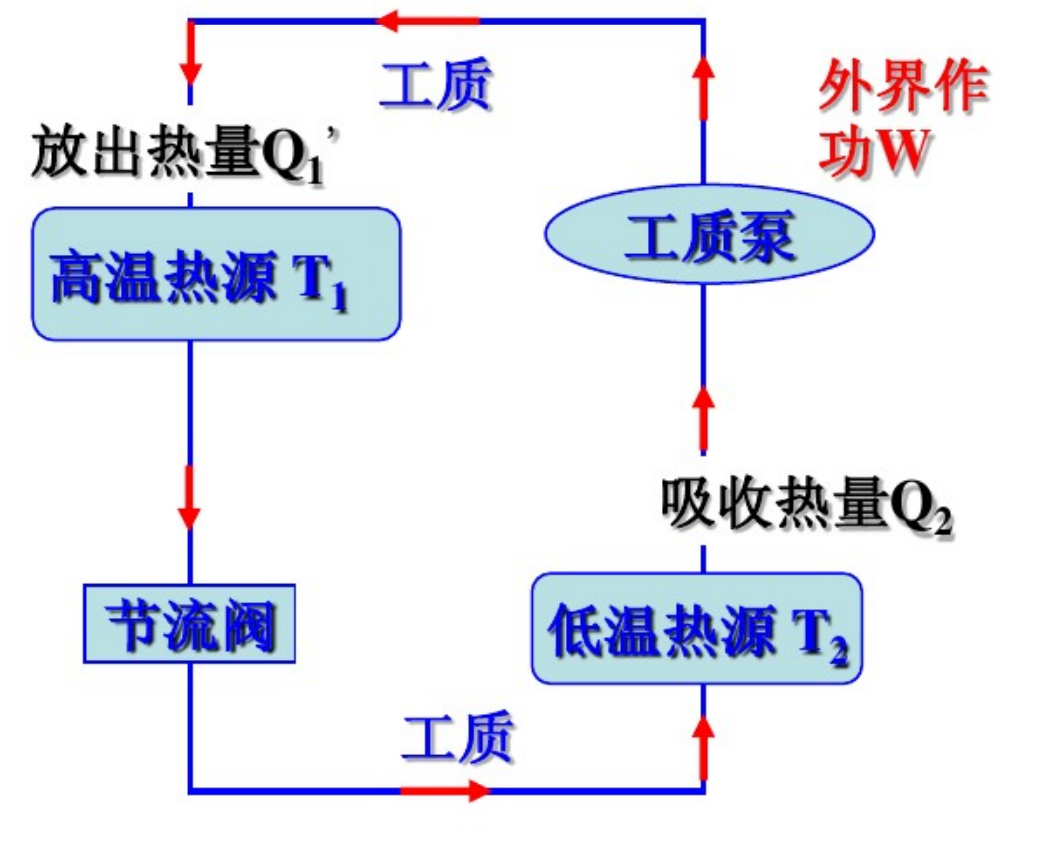
制冷机

$$e=\frac{Q_2}{W}=\frac{Q_2}{Q_1'-Q_2}$$

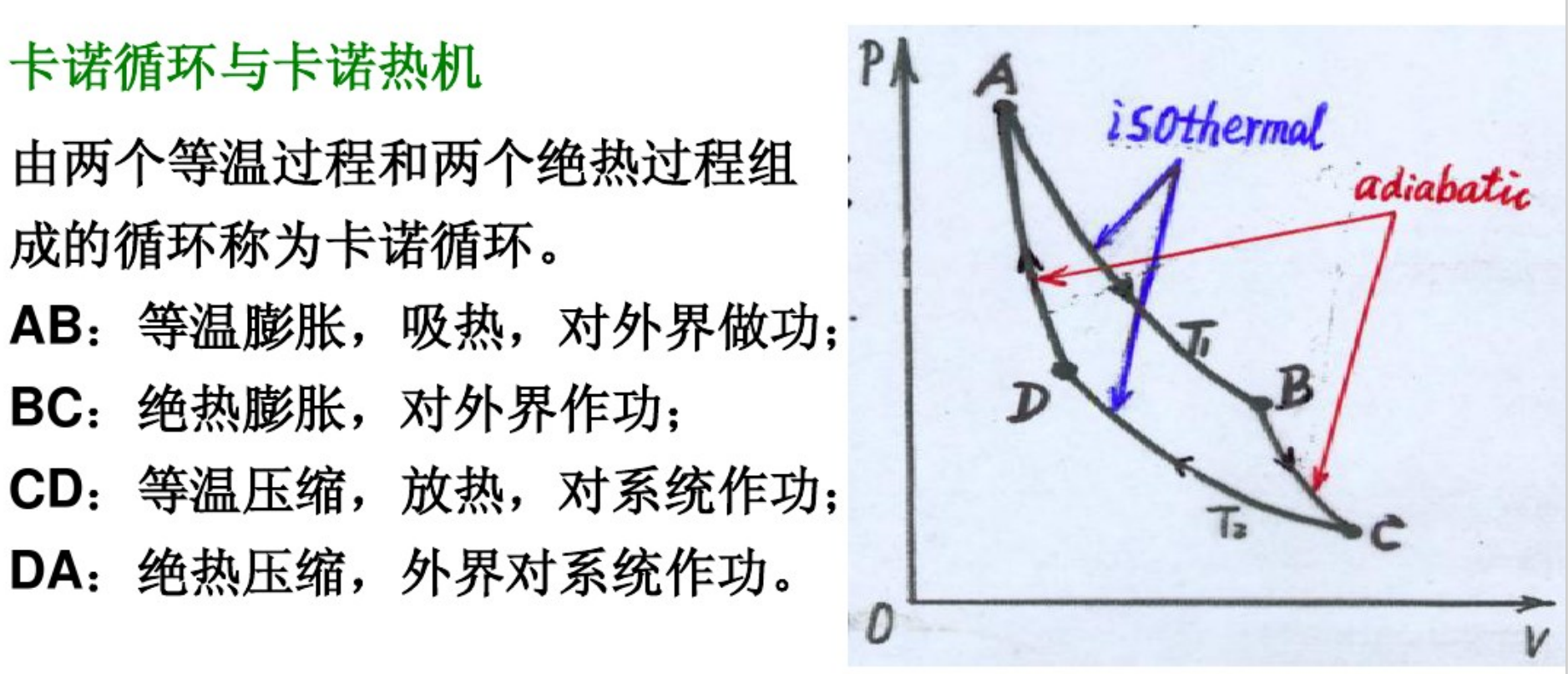
卡诺循环

$$\eta=\frac{T_{1}-T_{2}}{T_{1}}=1-\frac{T_{2}}{T_{1}}$$ $$\varepsilon=\frac{Q_{2}}{W}=\frac{Q_{2}}{Q_{1}-Q_{2}}=\frac{T_{2}}{T_{1}-T_{2}}$$

气体动理论

分子与分子之间存在着一定的间距

分子之间存在着相互作用力，注意$r_0$

分子在不断的做无谓的运动，布朗运动

利用统计学方法来研究气体

分布

速率分布函数

$$f(v)=\lim_{\Delta v\to0}\frac{\Delta N}{N \Delta v}\\ \int_0^{+\infty}f(v)\text{d}v=1$$

只有积分是具有实际意义的，单个值不具有任何意义

平均速率

$$\overline{v}=\frac{\int v\text{d}N}{N}=\int vf(v)\text{d}v\\=\sqrt{\frac{8RT}{\pi M}}=1.6\sqrt{\frac{RT}{ M}}$$

方均根速率

$$\overline{v^2}=\frac{\int v^2\text{d}N}{N}=\int v^2f(v)\text{d}\\\sqrt{\overline{v^2}}=\sqrt{\frac{3RT}{ M}}=1.73\sqrt{\frac{RT}{ M}}$$

最概然速率

$$v_p=\sqrt{\frac{2RT}{ M}}=1.41\sqrt{\frac{RT}{ M}}$$

气体压强

$$p=\frac23n\overline\varepsilon_k \\ \overline\varepsilon_k=\frac12m_0\overline{v^2}=\frac32kT\\ \Rightarrow p=nkT$$