大一/物理/振动

简谐振动

弹簧振子

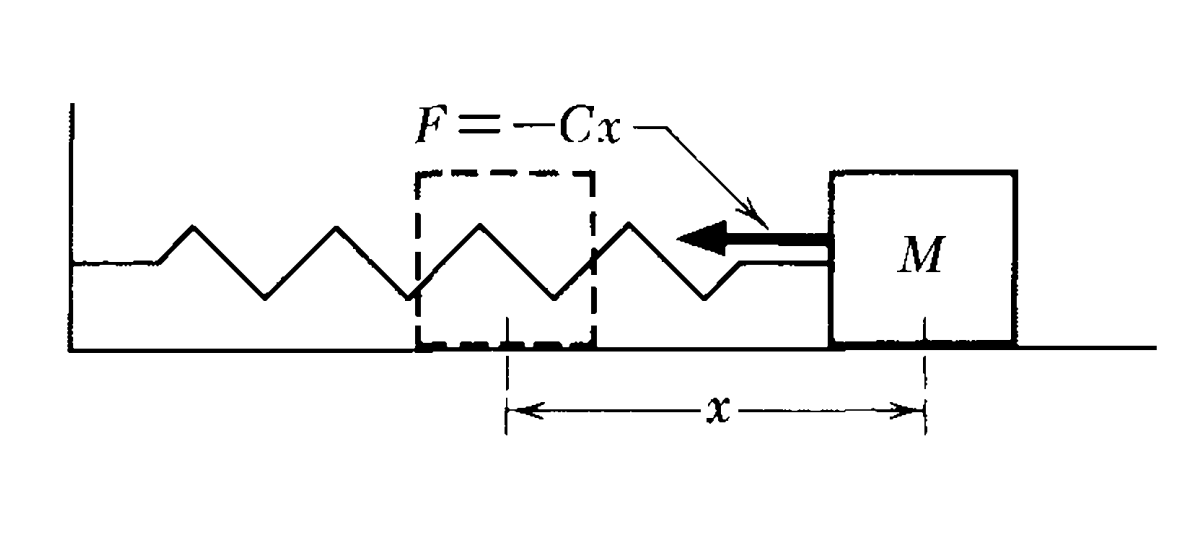对于一个从平衡位置出发的物体，若其受力直接正比于其偏离平衡位置的位移，即满足如下方程

$$\boldsymbol{F}=-k\boldsymbol{x}\\ \frac{\text{d}^2x}{\text{d}t^2}=-\frac km x=-\omega_0^2x$$

则该微分方程的解为

$$x=A\cos(\omega_0t+\varphi)\\ v=-A\omega_0\sin(\omega_0t+\varphi)\\ a=-A\omega_0^2\cos(\omega_0t+\varphi)=-\omega_0^2x$$

其中$\omega_0$为该简谐振动的角频率

由机械能守恒两边对时间求导同样可以得到结果

单摆

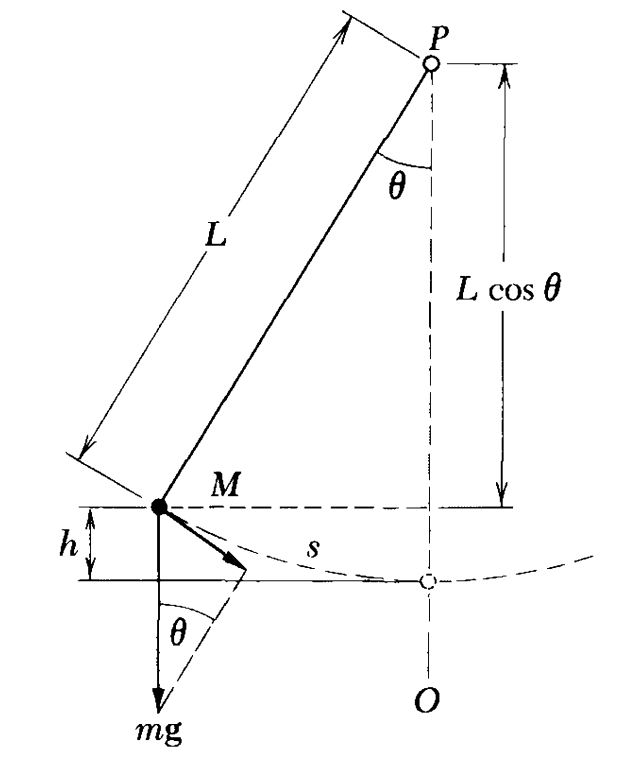
在角度较小时，由小角度近似$\sin \theta\approx\theta$

$$\frac{\text{d}^2\theta}{\text{d}t^2}=-\frac{g}{L}\theta$$

由于$\theta\approx 0$

$$\frac{\text{d}^2x}{\text{d}t^2}=-\frac gL x$$

结果为

$$\theta =\theta_0\cos(\omega_0t+\varphi)\\ \omega_0=\sqrt{\frac gL}\\ T_0=2\pi\sqrt{\frac Lg}$$

重要物理量

$$A=\sqrt{x_0^2+\left(\frac{v_0}{\omega_0}\right)^2}\\ \varphi=\arctan\left(-\frac{v_0}{\omega_0x_0}\right)$$

利用选择矢量法可以方便地求出各物理量

能量

$$E_p=\frac12kx^2\\ E=E_p+E_k=\frac12kA^2\\ \overline{E_k}=\overline{E_p}=\frac14kA^2$$

振动的合成

同频率

对于两个同频率的简谐振动，运动具有相对静止性

$$\Delta\varphi=\varphi_2-\varphi_1$$

若$\Delta\varphi=2k\pi$则为同相，振动加强，振幅最大

$$A=A_1+A_2$$

$\Delta\varphi=(2k+1)\pi$则振动削弱，合振幅最小

$$A=|A_1-A_2|$$

一般的

$$A=\sqrt{A_1^2+A_2^2+2A_1A_2\cos\Delta\varphi}\\ \tan\varphi=\frac{A_1\sin\varphi_1+A_2\sin\varphi_2}{A_1\cos\varphi_1+A_2\cos\varphi_2}$$

不同频率

若频率相差不大，则振幅会出现时大时小的现象，称为拍

若两次重合则为合拍

$$T=\frac{2\pi}{\omega_{\text{raletive}}}=\frac{2\pi}{\omega_2-\omega_1}\\ \nu=\frac1T=\nu_2-\nu_1$$

其中$\nu$称为拍频

相互垂直的简谐振动

振动$1$与$x$轴上，振动$2$于$y$轴上

若$\varphi_2-\varphi_1=2k\pi$

则$y=\frac{A_2}{A_1}x$为线振动

若$\varphi_2-\varphi_1=(2k+1)\pi$

则$y=-\frac{A_2}{A_1}x$为线振动

若$\varphi_2-\varphi_1=\pm\frac\pi2$

$$\frac{x^2}{A_1^2}+\frac{x^2}{A_1^2}=1$$

振动的分解

利用傅里叶变换可将一个角频率为$\omega$的振动分解为

$$f(t)=A_0+\sum_{n=1}^\infty{A_n\cos(n\omega t+\varphi_n)}$$

$\omega$称为基频，$n\omega$称为$n$次谐频

阻尼振动

$$m\frac{\text{d}^2x}{\text{d}t^2}=-kx-\gamma\frac{\text{d}x}{\text{d}t}$$

令$\omega_0^2=\frac km,2\beta=\frac\gamma m$

$$\frac{\text{d}^2x}{\text{d}t^2}+2\beta\frac{\text{d}x}{\text{d}t}+\omega_0^2x=0$$

则为阻尼振动

小阻尼

$$x=A_0e^{-\beta t}\cos(\sqrt{\omega_0^2-\beta^2}t+\varphi_0)$$

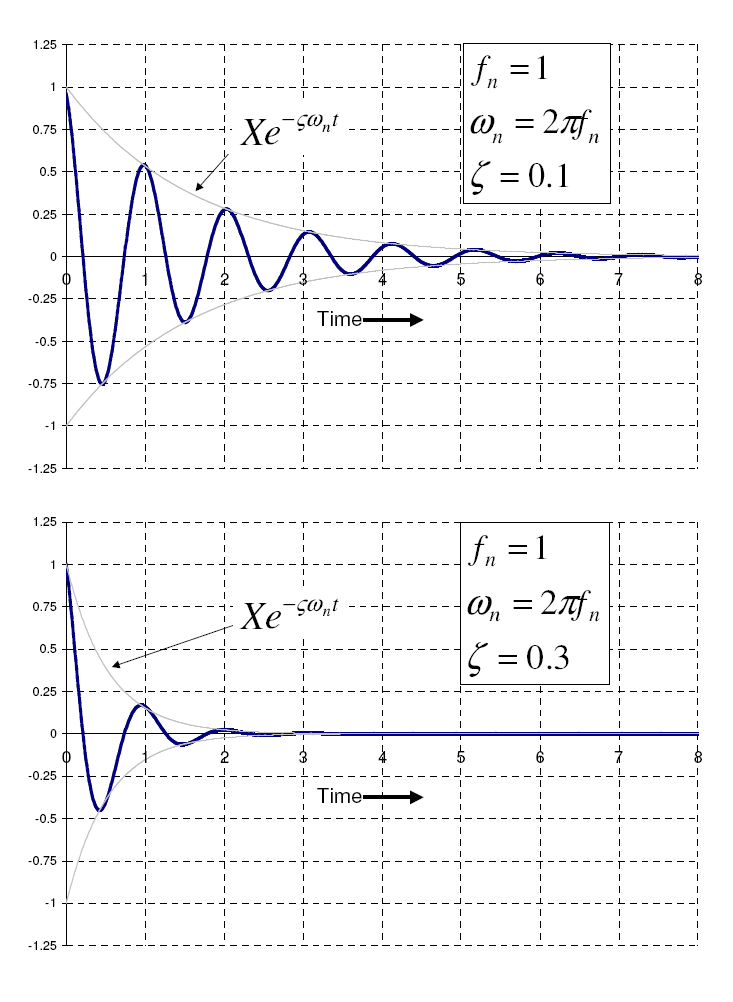
阻尼振动的周期比固有周期要长

大阻尼

$$\beta>\omega_0$$

不能完成一个周期运动，将缓慢移到平衡位置

临界阻尼

物体从运动到静止在平衡位置所需时间最短

受迫振动

$$F=F_0\cos\omega t$$

小阻尼下受迫振动为阻尼振动和简谐振动的叠加

稳定后振动的表达式为

$$x=A\cos(\omega t+\varphi)$$

角频率和驱动力频率相等

共振

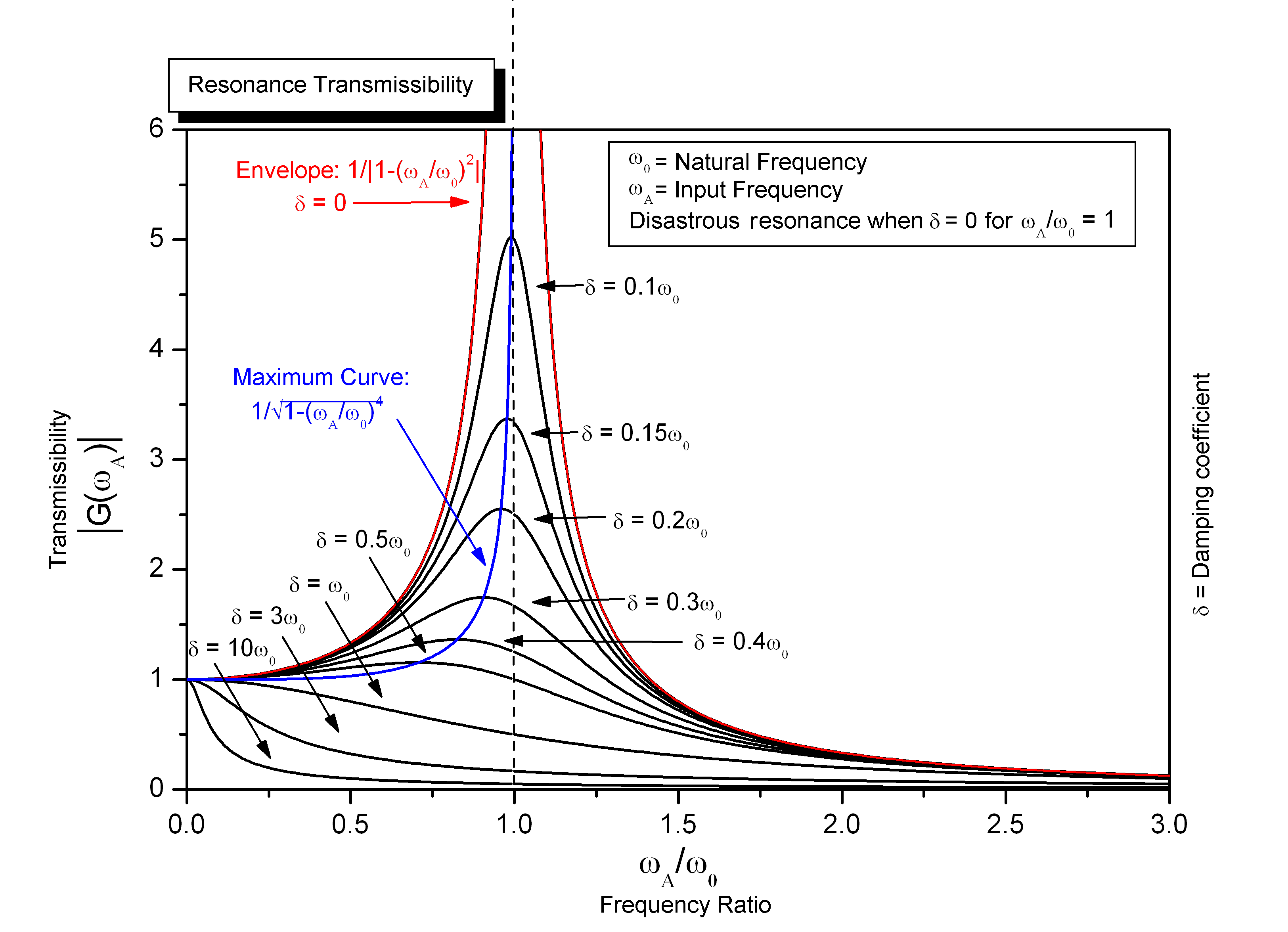
当驱动力频率为共振频率时，受迫振动的振幅达到峰值

$$\omega_r=\sqrt{\omega_0^2-2\beta^2}\\ A_r=\frac{f_0}{2\beta\sqrt{\omega_0^2-\beta^2}}$$

若阻尼很小，则振幅趋于无穷大

当$\omega=\omega_0$时，速度振幅达到最大，称为速度共振

机械波

自然界存在两种波

机械波只有在弹性介质中才能传播，如声波，水波

电磁波可在真空中传播

产生波一要有波源，二要有弹性介质

分类

横波振动方向和波传播方向垂直

纵波振动方向和波传播方向平行

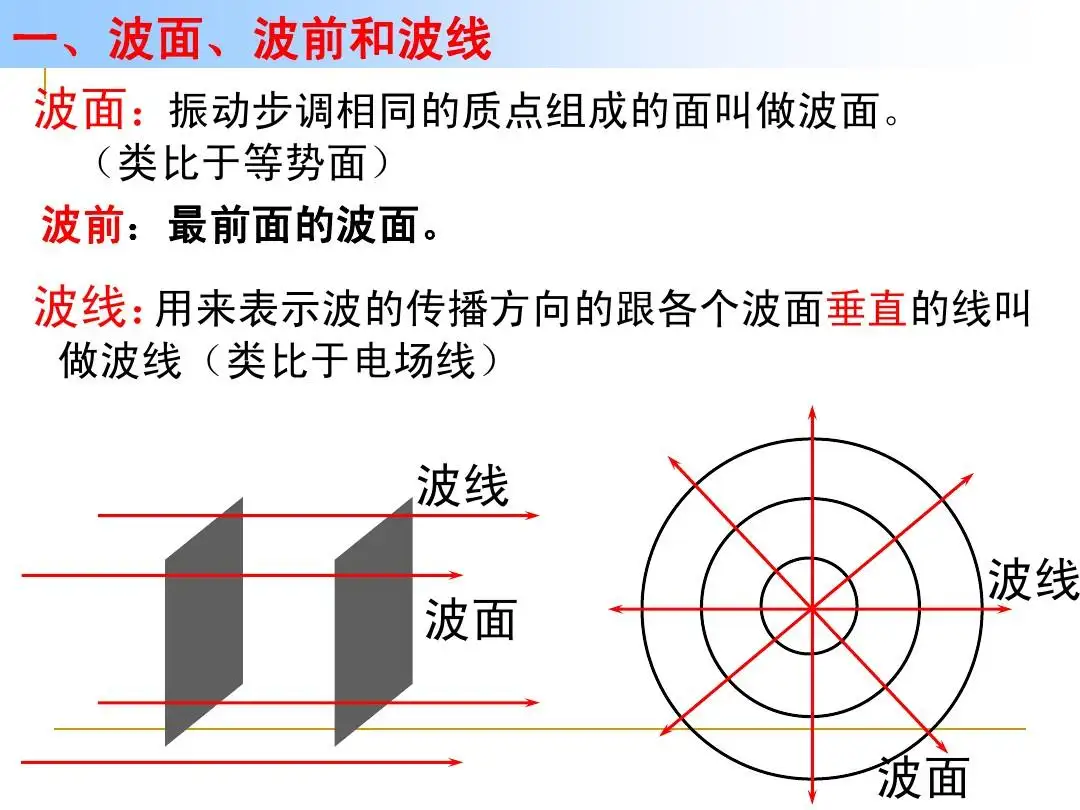
波速时振动在介质中的传播速度

$$u=\frac{\lambda}T$$

平面简谐波

$$\begin{aligned}y(x,t)&=A\cos\left[\omega\left(t-\frac x u\right)+\varphi_0\right]\\ &=A\cos\left(\omega t-\frac{2\pi x }\lambda +\varphi_0\right)\\ &=A\cos\left[2\pi\left(\frac tT-\frac x u\right)+\varphi_0\right]\\ \end{aligned}$$

$\Delta t$时间内，整个波向传播方向移动了$u\Delta t$的距离

这种在空间内行进的波称为行波

若不在原点，将$x$换为$x-x_0$

若沿反方向则对称，$x$换为$-x$

波的能量

$$\text{d}E_k=\text{d}E_p=\frac12\rho A^2\omega^2\sin^2\omega\left(t-\frac x u\right)\text{d}V\\ \text{d}E=\rho A^2\omega^2\sin^2\omega\left(t-\frac x u\right)\text{d}V$$

波的传播过程中，动能和势能变化完全同步

引入能量密度

$$w=\frac{\text{d}E}{\text{d}V}=\rho A^2\omega^2\sin^2\omega\left(t-\frac x u\right)\\ \overline{w}=\frac12\rho A^2\omega^2\propto A^2$$

平均能流为单位时间内垂直通过某一面积的平均能量

$$\overline{P}=\overline{w}uS=\frac12\rho A^2\omega^2uS$$

单位时间内垂直通过单位面积的平均能量称为流能密度或波的强度

$$I=\frac{\overline{P}}S=\frac12\rho A^2\omega^2u$$

声波

声压

$$p=\rho uv$$

声压和速度成正比，故和时间空间作周期性变化

我们把$Z=\rho u$称为特征阻抗

阻抗大的为波密介质，反之为波疏介质

声强

$$I=\frac{\overline{P}}S=\frac12\rho A^2\omega^2u$$ $$p_{\text{m}}=\rho uv_{\text{m}}=\rho u\omega A\\ I=\frac12\frac{p_\text{m}}{\rho u}$$

对于人耳对声音的主观感受，引入声强级的概念

$$L=\lg \frac I{I_0}$$

其中$I_0$为标准声强，单位为贝尔、

贝尔单位较大，用常用分贝来表示

$$L=10\lg \frac I{I_0}\quad (\text{dB})$$

波的干涉

波有叠加原理，可以单独看每一个波，波之间不会相互影响

但任一质元的振动是叠加之后的结果

对于频率，振动方向相同的两列波，称之为相干波

对于一点$P$距离两个波源的距离分别为$r_1,r_2$

$$y_{1P}=A_1\cos\left(\omega t+\varphi_1-\frac{2\pi r_1}\lambda\right)\\ y_{2P}=A_2\cos\left(\omega t+\varphi_2-\frac{2\pi r_2}\lambda\right)$$

由简谐振动的合成规律知

$$A=\sqrt{A_1^2+A_2^2+2A_1A_2\cos\left[(\varphi_2-\varphi_1)-\frac{2\pi (r_2-r_1)}\lambda\right]}\\ \tan\varphi=\frac{A_1\sin\left(\varphi_1-\frac{2\pi r_1}\lambda\right)+A_2\sin\left(\varphi_2-\frac{2\pi r_2}\lambda\right)}{A_1\cos\left(\varphi_1-\frac{2\pi r_1}\lambda\right)+A_2\cos\left(\varphi_2-\frac{2\pi r_2}\lambda\right)}$$

又因为$I\propto A^2$

$$I=I_1+I_2+2\sqrt{I_1I_2}\cos\Delta\varphi$$

相位差

$$\Delta\varphi=(\varphi_2-\varphi_1)-\frac{2\pi (r_2-r_1)}\lambda$$

若

$$\Delta\varphi=2k\pi$$

则称这些点为干涉相长点

$$A_{\text{max}}=A_1+A_2\\ I_{\text{max}}=I_1+I_2+2\sqrt{I_1I_2}$$

因为干涉相消而引起振幅和强度减小

$$\Delta\varphi=(2k+1)\pi$$

若$\varphi_2=\varphi_1$

则干涉条件可简化为

$$\delta=r_2-r_1=\begin{cases}\pm k\lambda,A_{\text{max}}=A_1+A_2\\ \pm \frac12(2k+1)\lambda,A_{\text{max}}=|A_1-A_2|\end{cases}$$

驻波

两列相干波在同一直线上沿相反方向传播时叠加形成的

$$y_{1}=A\cos\left(\omega t-\frac{2\pi x}\lambda\right)\\ y_{2}=A\cos\left(\omega t+\frac{2\pi x}\lambda\right)$$

由和差化积公式

$$\cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}2\cos\frac{\alpha-\beta}2$$

有

$$y=y_1+y_2=2A\cos\left(\frac{2\pi x}\lambda\right)\cos\omega t$$

上式被称为驻波方程

特殊位置

$$\left|\cos\frac{2\pi x}\lambda\right|=1\Rightarrow x= k\frac\lambda2$$

振幅最大，称为波腹

$$\left|\cos\frac{2\pi x}\lambda\right|=0\Rightarrow x= (2k+1)\frac\lambda4$$

振幅为$0$，称为波节

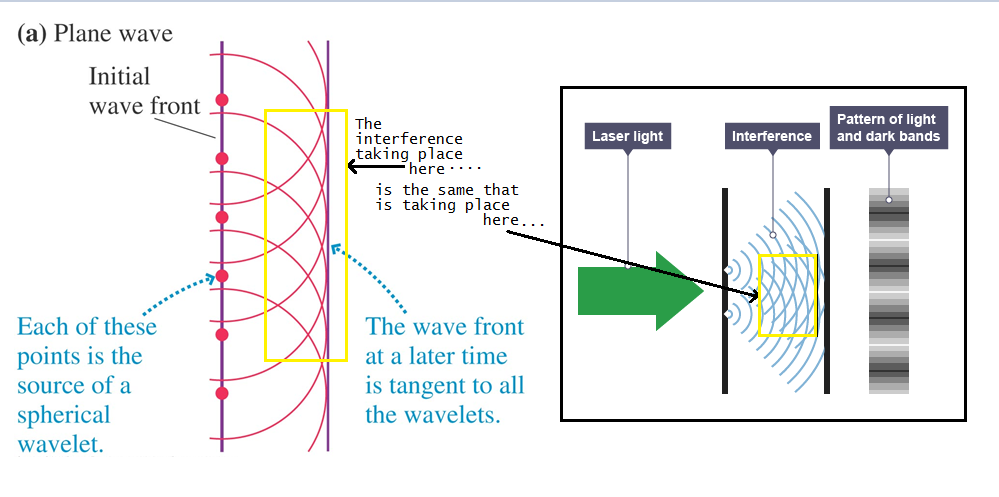
惠更斯原理

波面上任意一点都可看作子波的波源

多普勒效应

$$\nu'=\frac{u+v_o}{u-v_s}\nu$$

其中$v_o$为观察者的速度，$v_s$为波源的速度，相向为正

马赫锥

$$\sin\theta=\frac{ut}{v_st}=\frac1{Ma}$$

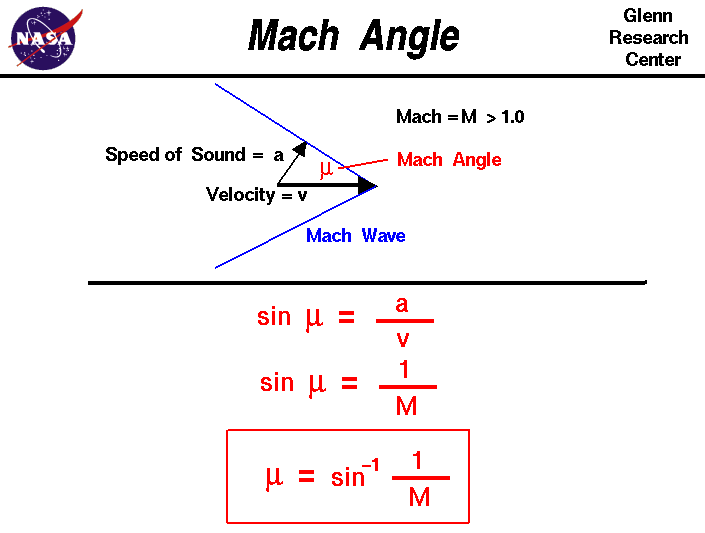
马赫数即为几倍声速