原函数和不定积分
原函数
若函数在区间$I$上连续,一定有原函数
显然这只是一个充分条件
反例有$x^2\sin \frac1x$,同时$e^{x^2}$的原函数不为初等函数
不定积分
带有任意常数项的原函数为不定积分
其中$x$为积分变量,$\displaystyle \int$为积分号,$f(x)$为被积函数
$f(x)\text{d}x$为被积表达式
第一类换元法
凑微分法,将表达式中的一个式子换元为$t$
根式有理函数
用于升高次数
欧拉代换
组合积分法
第二类换元法
类似于参数方程,用于化简表达式
常用代换
熟练运用半角公式,倍角公式,积化和差
万能代换
分部积分法
反对幂三指$=u$
表格法

上方为$u$下方为$v$,上方求导下方积分
分部积分的$\displaystyle\int v\text{d}u$部分可保留后续可消去
对于反三角函数或$\ln^2(x)$我们令$\text{d}x=\text{d}v$
积分的递推公式
我们可以通过分部积分来获得递推关系
有理函数的积分
利用多项式除法,总可以将一个假分式改写成一个多项式和一个真分式之和
对于真分式,讨论分母
如果分母中有因式$(x-a)^k$
如果分母中有因式$(x^2+px+q)^k$
具体计算时使用极限法和特殊值带入法
例
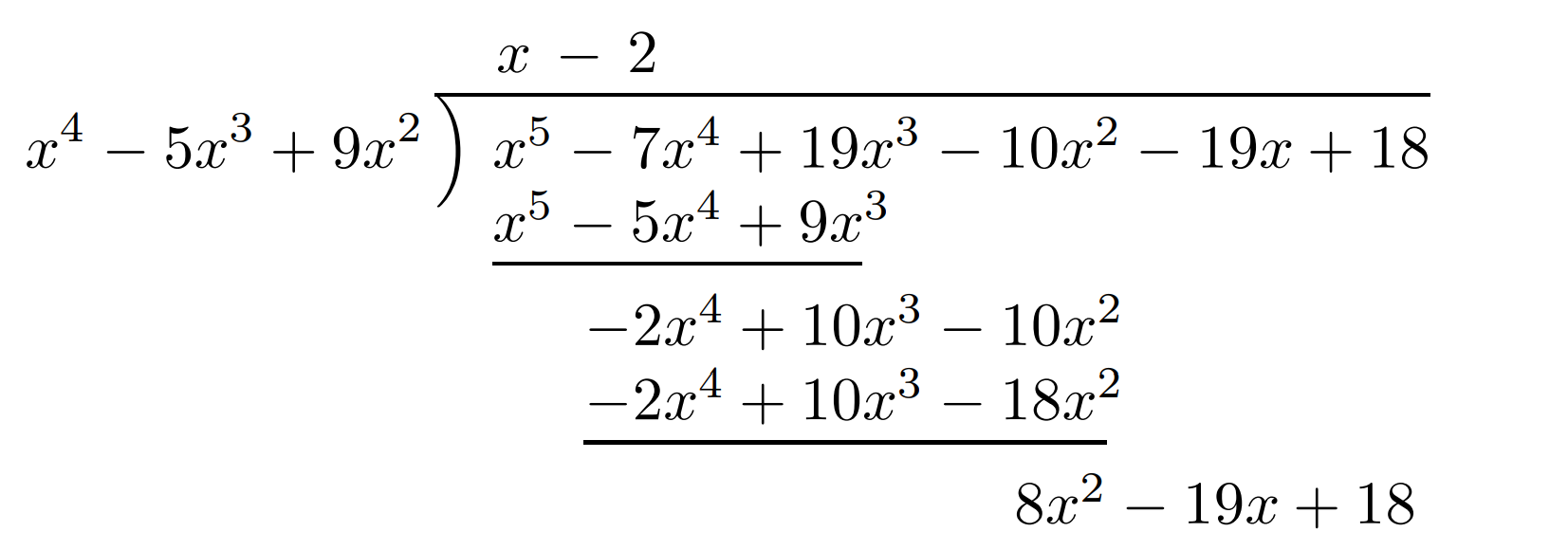
所以答案为
解题细节
- 先需要写出微分关系
- 步骤无需太细微,在草稿纸上完成
- 结果一定要用$x$来表示
- 不定积分一定需要加常数$C$
定积分
定义
特别的,若对于$[0,1]$上的积分,有
此公式常用于求极限
定积分的几何意义是图线围成的有向面积$(\text{signed area})$
连续必可积,若有界且只有有限个间断点也可积
性质
交换上下限,结果相反
定积分的可加性
一条线的面积为$0$
定积分的线性性质
$f(x)$和$g(x)$之间围成的面积
定积分的估值定理
积分中值定理
保号性
绝对值不等式
第一基本定理
则函数$F(x)$可导且满足
我们称$F(x)$为积分上限函数(原函数中的一个)
第二基本定理
这个公式给出了定积分的一般计算方法,具有普遍意义
由此我们知道定积分和不定积分有着密切联系
从而推知分部积分和换元积分在定积分中都可以使用
特殊性质
奇函数
奇函数在对称区间上的积分为$0$
偶函数
三角函数
周期函数
积分值和$a$的选取无关
区间再现公式
积分对称原理
若$f(x) $关于$\frac{a+b}{2}$对称,根据区间再现公式
Gamma
分部积分得
对于正整数
特别的,对于$x\in(0,1)$
反常积分
无界区间
积分区间无限或被积函数被积函数无界的积分,称为反常积分
存在,则称反常积分
收敛,同理
只有两个积分都收敛则原积分收敛
无界函数
$f(x)$在$x=b$的左邻域无界,$\forall \eta\in(0,b-a)$,$f(x)$在$[a,a+\eta]$可积有界
则称反常积分收敛,否则为发散
求积分
这种方式不仅可以判定散敛性还可以求出值
p积分
当$p>1$时积分收敛,$p\le1$
在$[0,1]$上正好相反