质点运动学

运动

质点为一个简化的忽略形状的物体，我们在选定的参考系(被选定的参考物体)下研究这个质点的运动情况

位矢

首先选取坐标原点，由此定义位矢$\vec r$

$\vec r=x \vec i+y\vec j+z\vec k$

位矢的方向由下式确定

$\cos \alpha=\frac x r,\cos \beta =\frac yr,\cos \gamma=\frac z r$

从而可以写出质点的运动方程

$\vec{r}=\vec{r}(t)=x(t) \vec i+y(t)\vec j+z(t) \vec k$

对于某一段过程，我们可以很自然地表示位移

$\Delta\vec r=\vec r(t_2)-\vec r(t_1)$

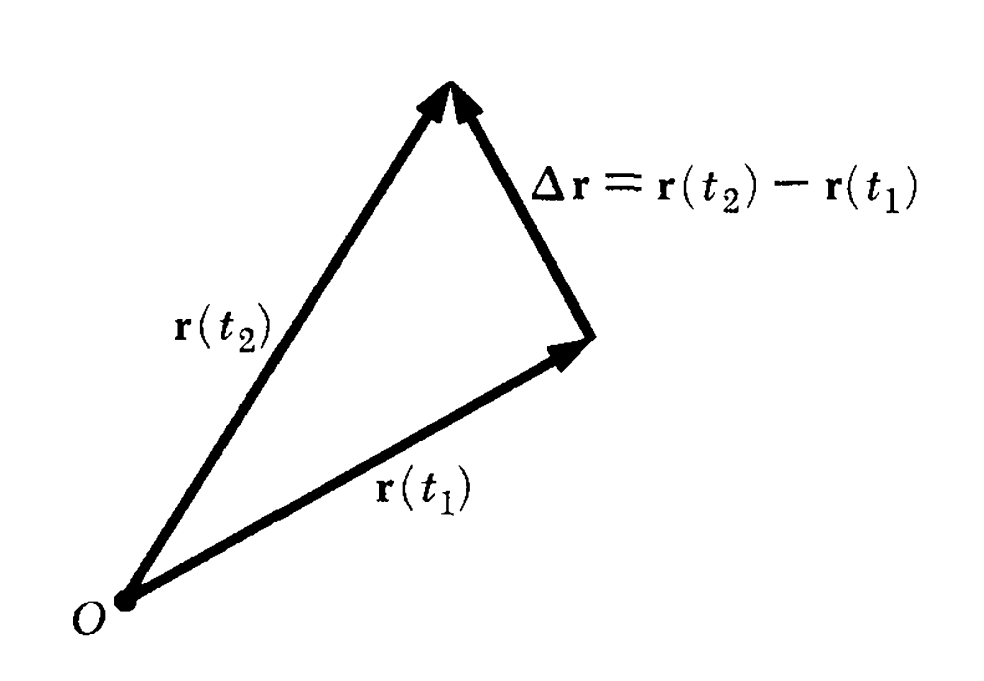
位移为矢量，$|\Delta\vec r|$表示两点的直线距离

速度

为了描述质点运动的快慢，我们引入速度的概念

$\overline{\vec v}=\frac{\vec r(t_2)-\vec r(t_1)}{t_2-t_1}$

这就是在某一段时间内的平均速度，方向为位移方向

当两个点$P_1,P_2$不断接近，割线变为切线

故速度也沿着切线方向

$\vec v=\lim_{\Delta t\to 0}\frac{\Delta \vec r}{\Delta t}=\frac{\text{d}\vec r}{\text{d}t}$

这也就是瞬间速度，$|\vec v|$被称为速率

同理可以正交分解，但还可以这样分解

在极坐标系下，有$r,\theta$两个参数

$\boldsymbol{v}=\frac{\text{d}r}{\text{d}t}\hat{\boldsymbol{r}}+r\frac{\text{d}\theta}{\text{d}t}\hat{\boldsymbol{\theta}}\\$

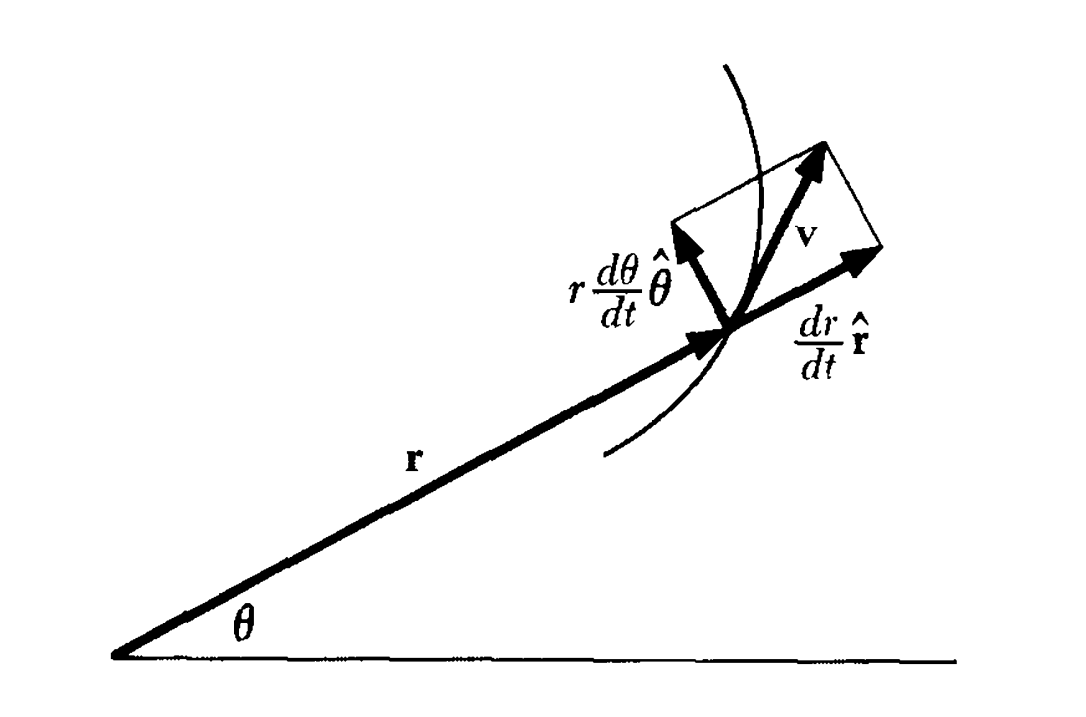
其中$\hat{\mathbf{r}}$是径向单位矢量，$\hat{\boldsymbol{\theta}}$是与径向垂直的单位矢量

加速度

同理，加速度即为速度对时间的导数，位移的二阶导数

$\vec a=\frac{\text{d}\vec v}{\text{d}r}= \frac{\text{d}^2\vec r}{\text{d}t^2}$

极坐标系下，有

$\boldsymbol{a}=\left[\frac{\text{d}^{2} r}{\text{d} t^{2}}-r\left(\frac{\text{d} \theta}{\text{d} t}\right)^{2}\right] \hat{\boldsymbol{r}}+\frac{1}{r}\left[\frac{\text{d}}{\text{d} t}\left(r^{2} \frac{\text{d} \theta}{\text{d} t}\right)\right] \hat{\boldsymbol{\theta}}$

自然坐标

因为速度延切线方向，故

$\boldsymbol{v}=\frac{\text{d}s}{\text{d}t}\boldsymbol{e}_t$

因为两个因子都是关于时间的函数

$\Rightarrow\vec a=\frac{\text{d}^2s}{\text{d}t^2}\boldsymbol{e}_t+v\frac{\text{d}\theta}{\text{d}t}\boldsymbol{e}_n$

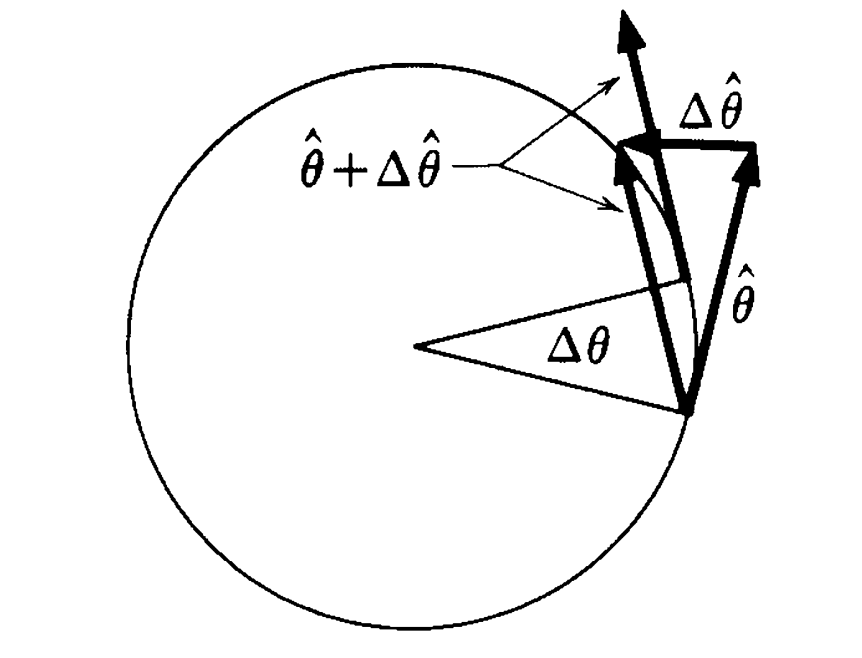
故可以分解为切向加速度和法向加速度

关系

质点的运动方程是描述质点运动的核心

其中$\vec r,\vec v$被称为运动状态量，加速度$\vec a$被称为状态变化量

圆周运动

法向加速度

$\boldsymbol{a}_n=\frac{v^2}r=\omega^2r=\omega v$ $\boldsymbol{a}=\frac{\text{d}}{\text{d}t}(\boldsymbol{\omega \times \boldsymbol{r}})=\boldsymbol{\alpha \times \boldsymbol{r}}+\boldsymbol{\omega \times \boldsymbol{v}}$

运动方程

利用圆的参数方程可得

$\vec r(t)=R\cos(\omega t )\vec i+R\sin(\omega t)\vec i$

重要关系

$T=\frac1f\\ \omega=2\pi f$

相对运动

$\boldsymbol{v}_{ac}=\boldsymbol{v}_{ab}+\boldsymbol{v}_{bc}\\ \boldsymbol{a}_{ac}=\boldsymbol{a}_{ab}+\boldsymbol{a}_{bc}\\$

推论，当某一加速度为$0$时，保持不变