大一/高数/导数

导数

切线

本质上是割线两个点趋向一起

$$y-y_0=f'(x_0)(x-x_0)$$

定义

若函数$f(x)$在点$x_0$处的某邻域有邻域可导，则

$$\left.\frac{\text{d}f(x)}{\text{d}x}\right|_{x=x_0}=\left.\frac{\text{d}y}{\text{d}x}\right|_{x=x_0}=f'(x_0) \\f'(x_0)=\lim_{\Delta x\to0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$$

同理$\Delta x\to0^-/0^+$可用于定义左右导数

可导

左右导数存在且相等(双侧)

可导一定连续，而连续不一定可导

• $y=|x|$有尖点

• 曲线光滑不一定可导

  $y=x^{\frac13},y’=\frac{1}{3x^{\frac23}},x\to0,y’=\infty$

• 导数存在不一定连续可导(导函数连续)

  $$f(x)=\begin{cases}x^2\sin \frac1x,x\ne0\\ 0,x=0\end{cases}$$

$n$阶可导$\Rightarrow$ $n-1$阶连续可导

上下无穷小必须同阶才可凑出导数形式

导数极限定理

如果$ f(x) $在$ x_0 $的邻域内连续，在$ x_0 $的去心领域内可导，且导函数在$ x_0 $出的极限存在，则$ f(x) $在$ x_0 $处的导数也存在并且等于导函数的极限

导函数左极限存在蕴含左导数存在，导函数右极限存在蕴含右导数存在

亚导数

将导数拓展到不可微的函数

$$y=|x|\\ \frac{\partial|x|}{\partial x}=\left\{\begin{array}{ll} 1 & \text { if } x>0 \\ -1 & \text { if } x<0 \\ a & \text { if } x=0, \end{array} \quad a \in[-1,1]\right.$$ $$\frac{\partial}{\partial x}\max(x,0)=\left\{\begin{array}{ll} 1 & \text { if } x>0 \\ 0 & \text { if } x<0 \\ a & \text { if } x=0, \end{array} \quad a \in[0,1]\right.$$

隐函数求导

等式左右两边看成两个函数

$$f(x)=g(x)\Rightarrow f'(x)=g'(x)$$

相关变化率

两个量具有相关性则它们的变化也具有相关性

参数方程求导

$$\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}t}\bigg/\frac{\text{d}x}{\text{d}t}$$

结果为关于$t$的函数

反函数

$$\frac{\text{d}y}{\text{d}x}=1\bigg/\frac{\text{d}x}{\text{d}y}$$

结果往往用$y$来表示，但是带入数值结果等价

(关于$y=x$对称故有此结果)

高阶导数

递推定义

$$f^{(n)}(x)=\begin{cases}[f^{(n-1)}(x)]',n\ge 1\\ f(x),n=0\end{cases}$$ $$(\sin x)^{(n)}=\sin(x+\frac{n\pi}2)\\ (\cos x)^{(n)}=\cos(x+\frac{n\pi}2)$$ $$(x^n)^{(n)}=n!,(x^n)^{(n+1)}=0$$ $$\left(\frac1x\right)^{(n)}=(-1)^n\frac{n!}{x^{n+1}}\\ \Rightarrow\left(\frac1{ax+b}\right)^{(n)}=({\color{red}{-a}})^n\frac{n!}{(ax+b)^{n+1}}\\$$

莱布尼兹公式

$$(uv)^{(n)}=\sum_{i=1}^nC_n^iu^{(n-i)}v^{(i)}$$

证明题使用数学归纳法来证明

相关性质

$f(x)$可导

• $f(x)$为奇$\Rightarrow f’(x)$为偶(不必要)
• $f(x)$为偶$\Leftrightarrow f’(x)$为奇

导数公式

$$(x^a)'=ax^{a-1}\\ (a^x)'=\ln a \cdot a^x \\(\log_ax)'=\frac{1}{\ln a\cdot x }\\ (\sin x)'=\cos x\\ (\cos x)'=-\sin x$$ $$[f(x)\pm g(x)]'=f'(x)\pm g'(x) \\ [f(x)\cdot g(x)]'=f'(x)g(x)+f(x)g'(x)\\ \left (\frac{f(x)}{g(x)}\right)'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\\ [f(g(x))]'=f'(g(x))\cdot g'(x)$$ $$\frac {\text{d}}{\text{d}x}(\tan x)=\sec^2x\\ \frac {\text{d}}{\text{d}x}(\cot x)=-\csc^2x\\ \frac {\text{d}}{\text{d}x}(\sec x)=\tan x \sec x\\ \frac {\text{d}}{\text{d}x}(\csc x)=-\cot x \csc x\\$$ $$\frac {\text{d}}{\text{d}x}(\arcsin x)=\frac1{\sqrt{1-x^2}}\\ \frac {\text{d}}{\text{d}x}(\arccos x)=-\frac1{\sqrt{1-x^2}}\\ \frac {\text{d}}{\text{d}x}(\arctan x)=\frac1{1+x^2}\\ \frac {\text{d}}{\text{d}x}(\text{arccot} x)=-\frac1{1+x^2}\\ \frac {\text{d}}{\text{d}x}(\text{arcsec} x)=\frac1{ { {\color{red}{|x|}}}\sqrt{x^2-1}}\\ \frac {\text{d}}{\text{d}x}(\text{arccsc} x)=-\frac1{ {\color{red}{|x|}}\sqrt{x^2-1}}\\ (\sinh x)'=\left(\frac{e^x-e^{-x}}2\right)' =\cosh x\\ (\cosh x)'=\left(\frac{e^x+e^{-x}}2\right)' =\sinh x\\$$ $$\frac{\text{d}}{\text{d} x} \cosh ^{-1}(x)=\frac{1}{\sqrt{x^{2}-1}}\\ \frac{\text{d}}{\text{d} x} \sinh ^{-1}(x)=\frac{1}{\sqrt{x^{2}+1}}$$

应用

单调性

本质定义

$$\forall x_1,x_2\in D,x_1<x_2,f(x_2)-f(x_1)>0\Rightarrow f(x)\uparrow$$

充分条件

若可导函数$f(x)$在$[a,b]$上单调增加，则在区间$(a,b)$上导数$f’(x)>0$

反过来

在区间$(a,b)$上导数$f’(x)>0$，则$f(x)$在$[a,b]$上单调增加

推论只有有限多个导数为$0$的点(驻点)，则这个函数仍单调增加

讨论三类边界点(驻点，不可导点)

例$y=(2x-5)\sqrt[3]{x^2}$

$$y'=\frac{10}3\frac{x-1}{\sqrt[3]{x}}$$

$x$	$(-\infty ,0)$	$0$	$(0,1)$	$1$	$(1,\infty)$
$f’(x)$	$+$		$-$	$0$	$+$
$f(x)$	$\uparrow$	$0$	$\downarrow$	$-3$	$\uparrow$

一般步骤

1. 求出驻点和不可导点(包括不连续)
2. 用上述这些点将定义域划分为若干区间
3. 判断$f’(x)$在每个区间上的符号
4. 整合结果得到单调性

凹凸性

$$\forall x_1,x_2\in D,f\left(\frac{x_1+x_2}2\right)>\frac{f(x_1)+f(x_2)}2$$

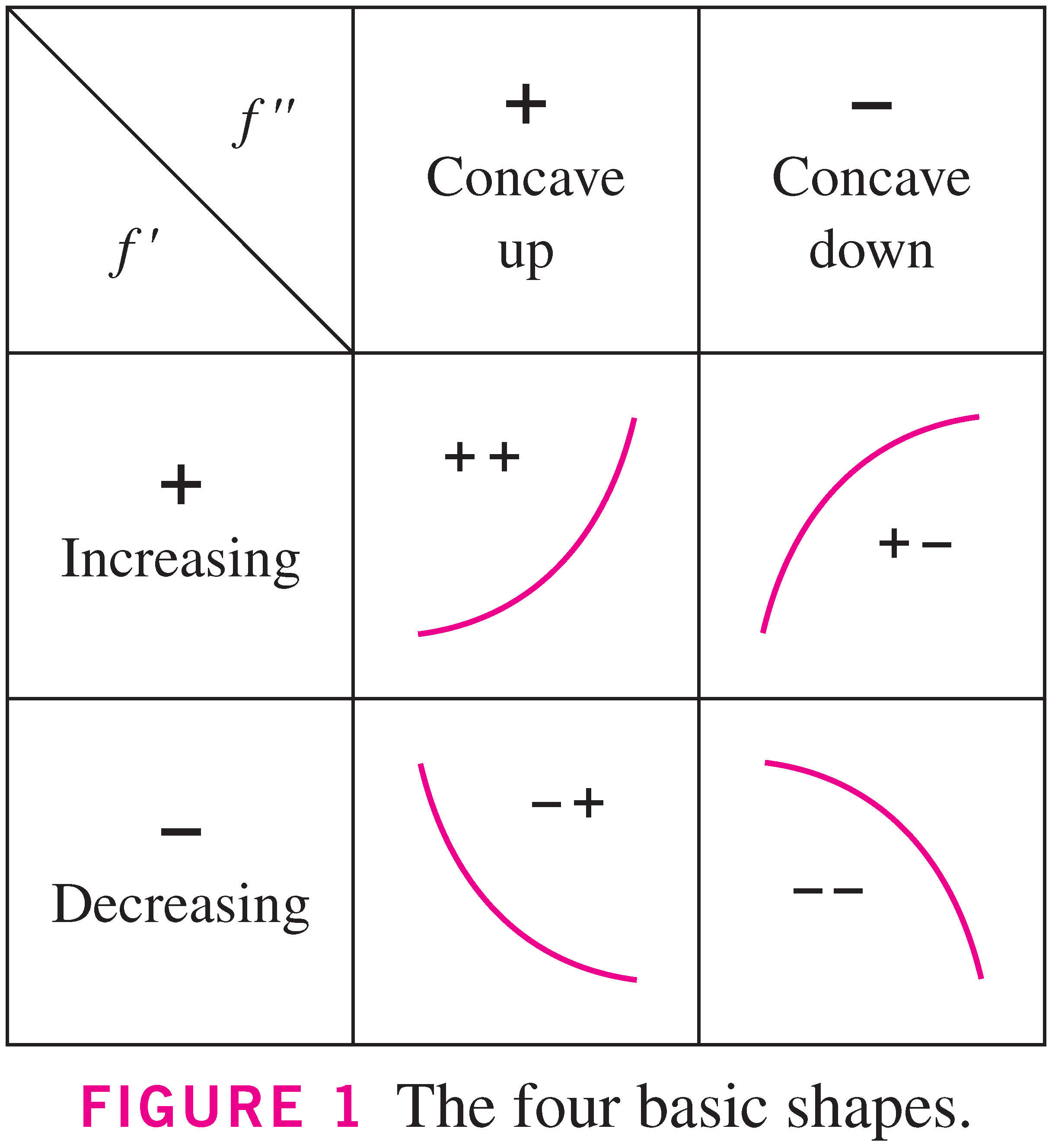
则称函数$f(x)$的图像在区间上是凸的或称为凸函数

推广

$$\forall x_i\in D,f\left(\sum_{i=1}^n\lambda_i x_i\right)>\sum_{i=1}^n\lambda_if(x_i)\quad \sum_{i=1}^n\lambda_i=1$$

拐点

连续曲线上凸弧和凹弧的分界点

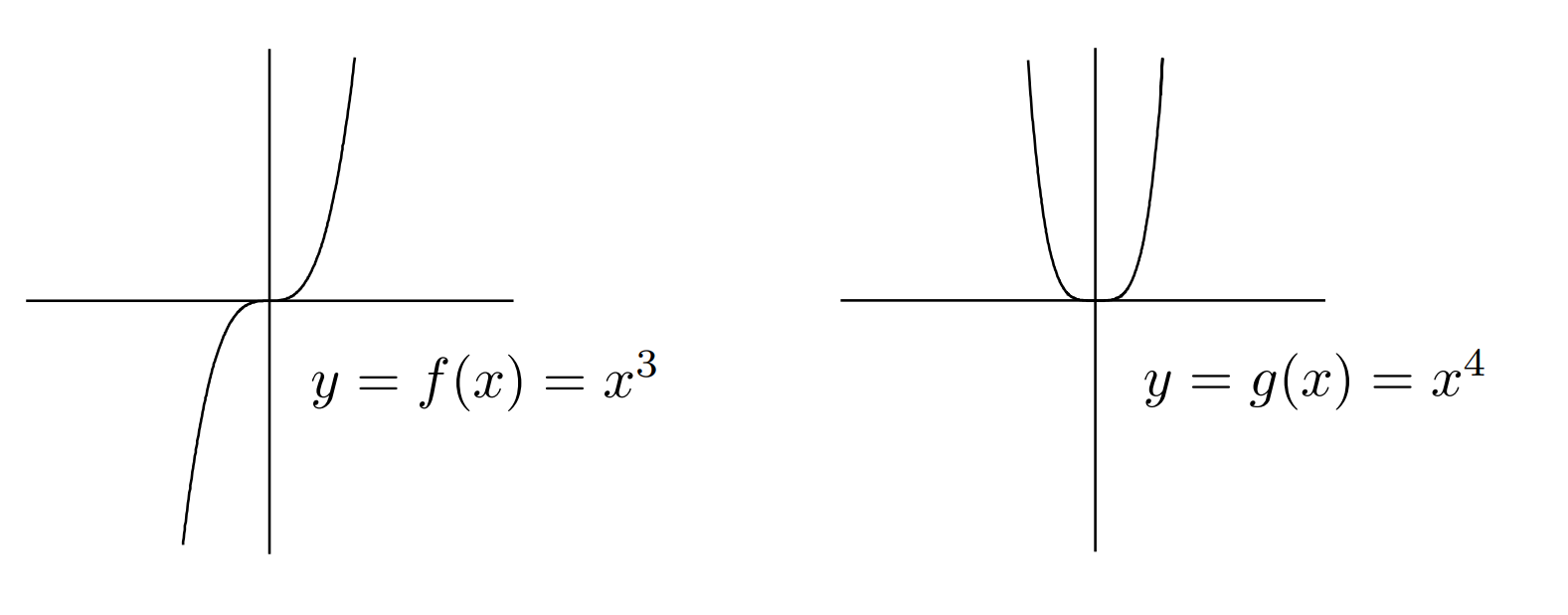
$f’’(x_0)=0$，则以上点都满足条件

$ (x_0,f(x_0))$可为有水平切线或为极值点

在该点不可导但仍可为拐点

同理$f’’(x_0)=0$还需看三阶导数

若函数在$x_0$有$2n+1 $阶导数

第一充分条件

==$f(x)$在$x_0$处连续==，且在，$\mathring{U}(x_0)$二阶可导

$$x\in\mathring{U}^-(x_0) ,f''(x)>0\\ x\in\mathring{U}^+(x_0) ,f''(x)<0$$

则$ (x_0,f(x_0))$为拐点

在两侧二阶函数异号

第二充分条件

类比$f’’’(x_0)\ne0$

第三充分条件

$$f'(x_0)=f''(x_0)=\cdots=f^{(2n)}(x_0)=0\\ f^{(2n+1)}(x_0) <0$$

极值

注意区分费马引理

若$\exists U(x_0)\subset D$，对于$\forall x\in \mathring{U}(x), f(x_0)>f(x_0)$

则称$f(x_0)$为函数的一个极大值

不一定要求连续，有定义就行，例如

极值定理

$\text{Extreme Value Theorem}$

$$\frac{f(c+h)-f(c)}{h}\\ A:\lim_{h\to0^+}\cdot\lim_{h\to0^-}<0\\ B:\lim_{h\to0}=0$$

推出若$x_0$为极值点则$f’(x_0)=0$为或不可导

判别法

第一充分条件

==$f(x)$在$x_0$处连续==，且在，$\mathring{U}(x_0)$可导

$$x\in\mathring{U}^-(x_0) ,f'(x)>0\\ x\in\mathring{U}^+(x_0) ,f'(x)<0$$

在两侧导函数异号

第二充分条件

若函数在$x_0$处有二阶导数

$$f'(x_0)=0,f''(x_0)<0$$

则为极大值点

第三充分条件

$$f'(x_0)=f''(x_0)=\cdots=f^{(2n-1)}(x_0)=0\\ f^{(2n)}(x_0) <0$$

类比为极小值点

最值

在区间$I$上，若对于任意$x\in I$，存在$x_0\in I$，都有$f(x)\le f(x_0)$

则称$f(x_0)$为函数在该区间上的最大值

若在闭区间$[a,b]$上连续，有限多个驻点和不可导点

则计算处各驻点$x_i$和不可导点$x’_j$

$$\max_{x\in[a,b]}f(x)=\max\{f(x_1),\cdots,f(x_i),f(x_1'),\cdots,f(x_j'),f(a),f(b)\}$$