向量
$\rm vector$ 表示
$||\vec{a}||$为向量的长度
在直角坐标系中
两向量之间的夹角为$0\le\left \langle \alpha,\beta \right \rangle \le \pi$
点乘
$\rm Dot\;Product$
矩阵
运算性质
叉乘
$\rm Cross \;Product$
运算性质
混合积
根据Levi-Civita
范数
表示
根据三角形法则,对于任何一个向量
都可以分解为两个基向量的线性组合
所有线性组合构成集合$\text{span}(\boldsymbol{i},\boldsymbol{j})$,称为张成空间
这就是向量的坐标表示法
直线的向量方程
对于直线,有如下关系
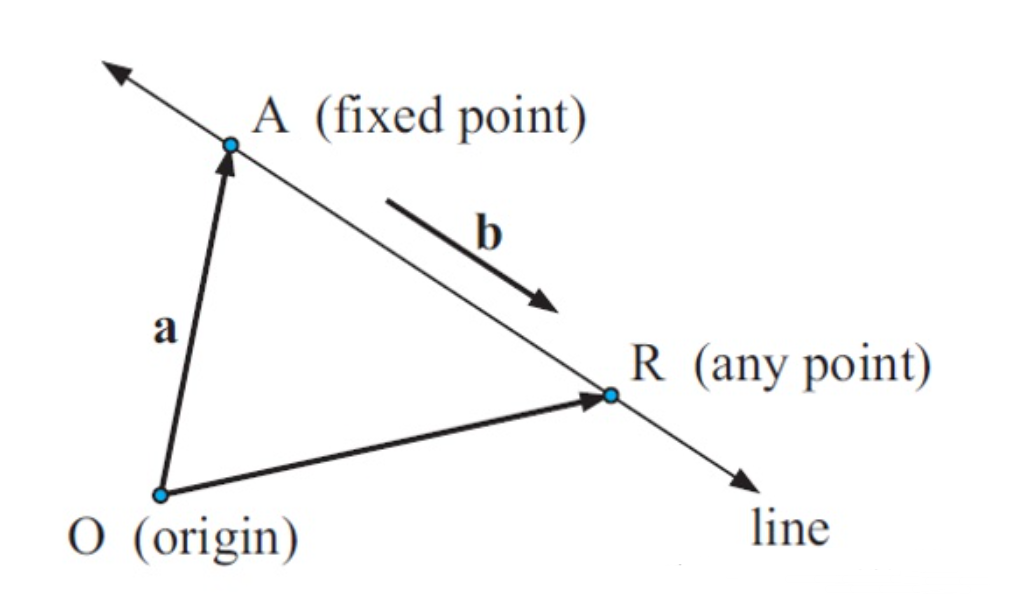
其中非零向量$\vec{AR}$为该直线的方向向量
写成坐标形式,可得
导数
求导的本质只是把标量求导的结果排列起来,至于是按行排列还是按列排列都是可以的
最基本的求导布局有两个:
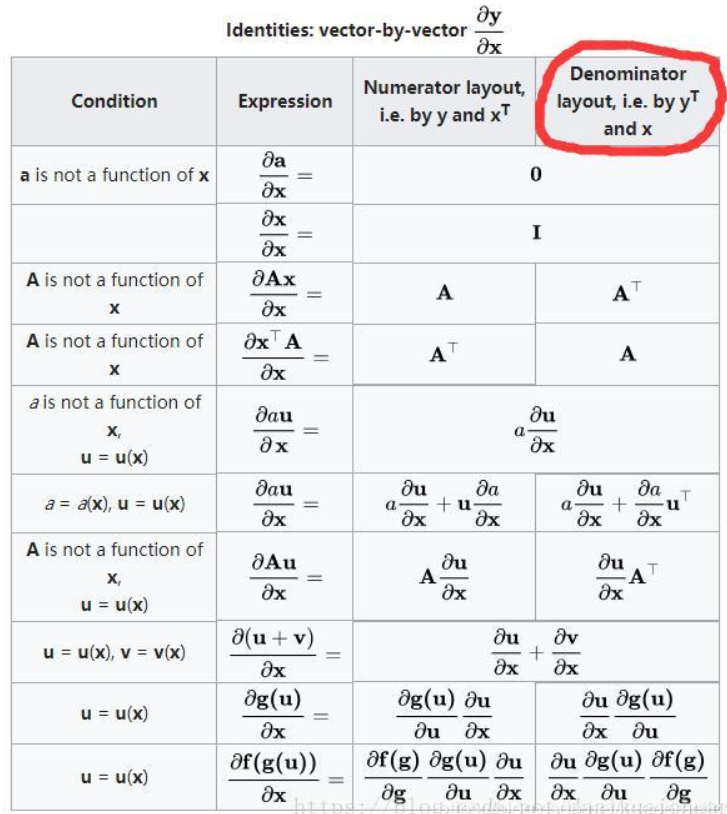
分子布局(numerator layout)和分母布局(denominator layout )
机器学习主要为分子布局
分子布局:分子为列向量,分母为行向量
方向导数,定义的$\rm shape$,例
求导运算是线性算子
雅可比矩阵
线性回归
求导
采用分子布局
场论
梯度
向量场里每个点赋予一个向量
散度
描述净流量,若流入大于流出则为负
$(x,y)$点生成的流量
例如对于不可压缩的流体
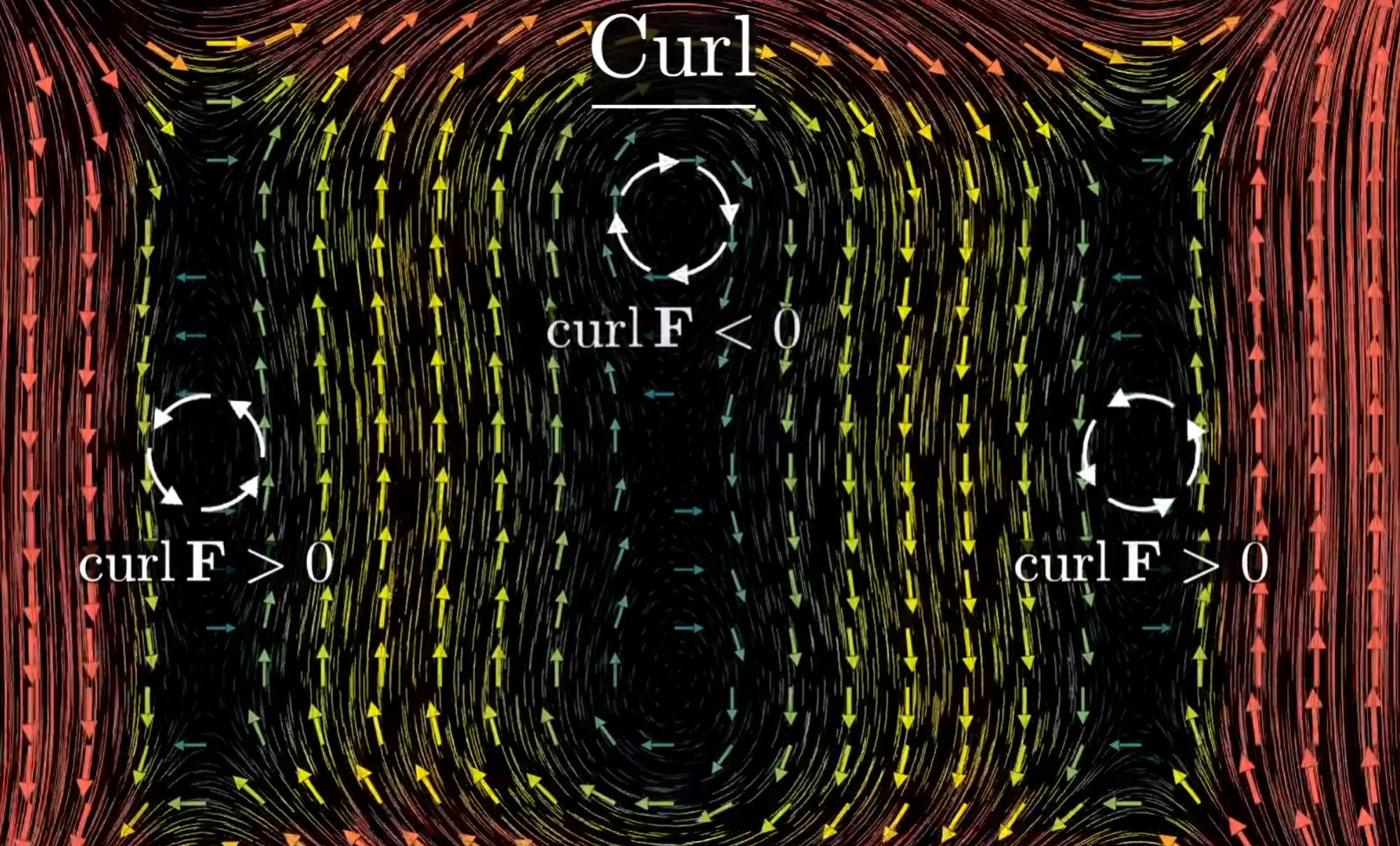
旋度