基本概念
例:$f(x)=x^2$
定义了一个函数 $f$ ,法则为将一个数转变为它的平方
未指定,故定义域为$\mathbf{R }$(实数集)
意义:$f(2)=4$,通过法则$f$将数字$2$转变为$4$
By the way, $f$ is the transformation rule, while $f(x)$ is the result of applying the transformation rule to the variable $x$. So it’s technically not correct to say “$f(x)$ is a function”; it should be “$f$ is a function.”
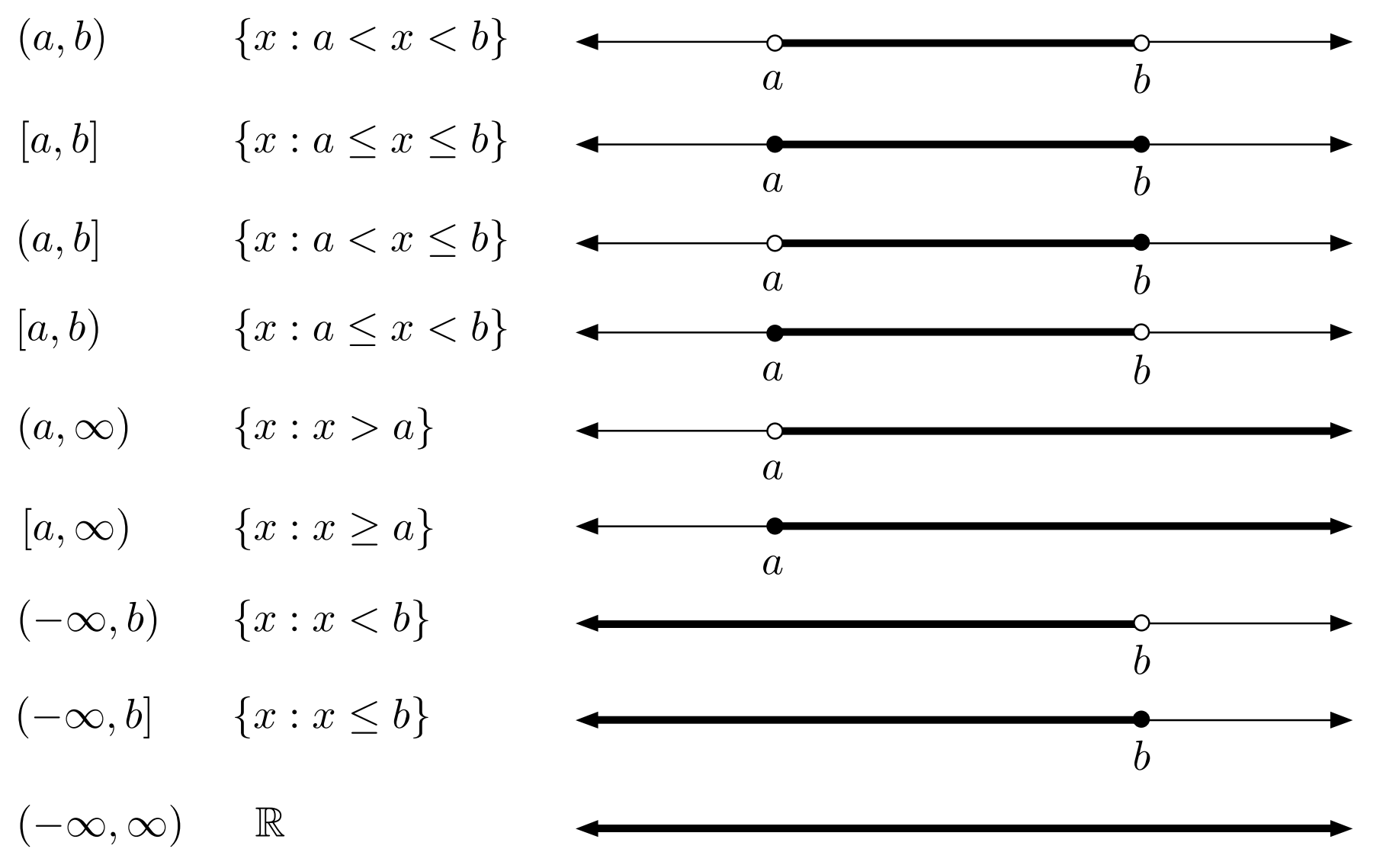
区间
函数
基本初等函数
常函数,幂函数,三角函数,反三角函数,对数函数,指数函数
初等函数是由基本初等函数经过==有限次==复合形成的能用一个式子表示的函数
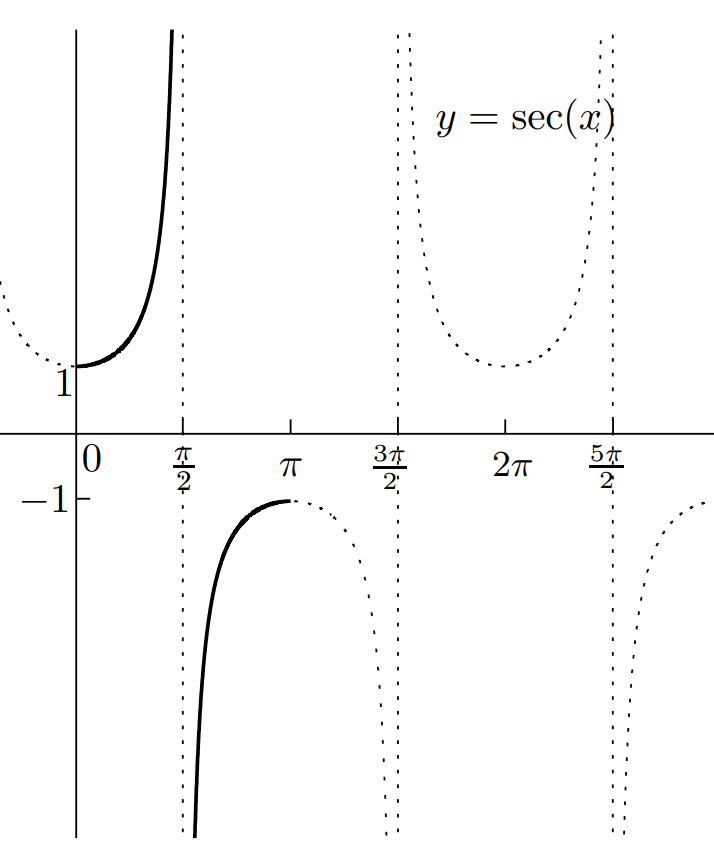
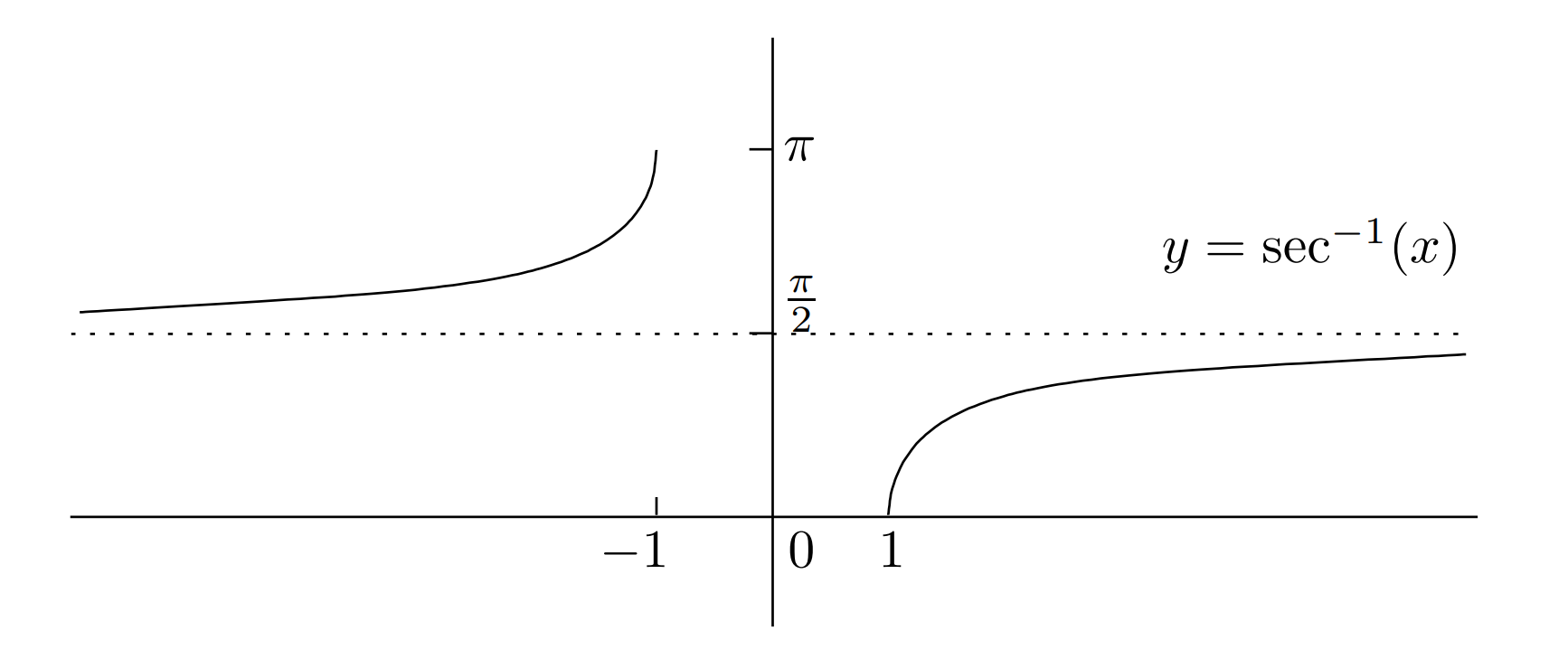
反三角函数
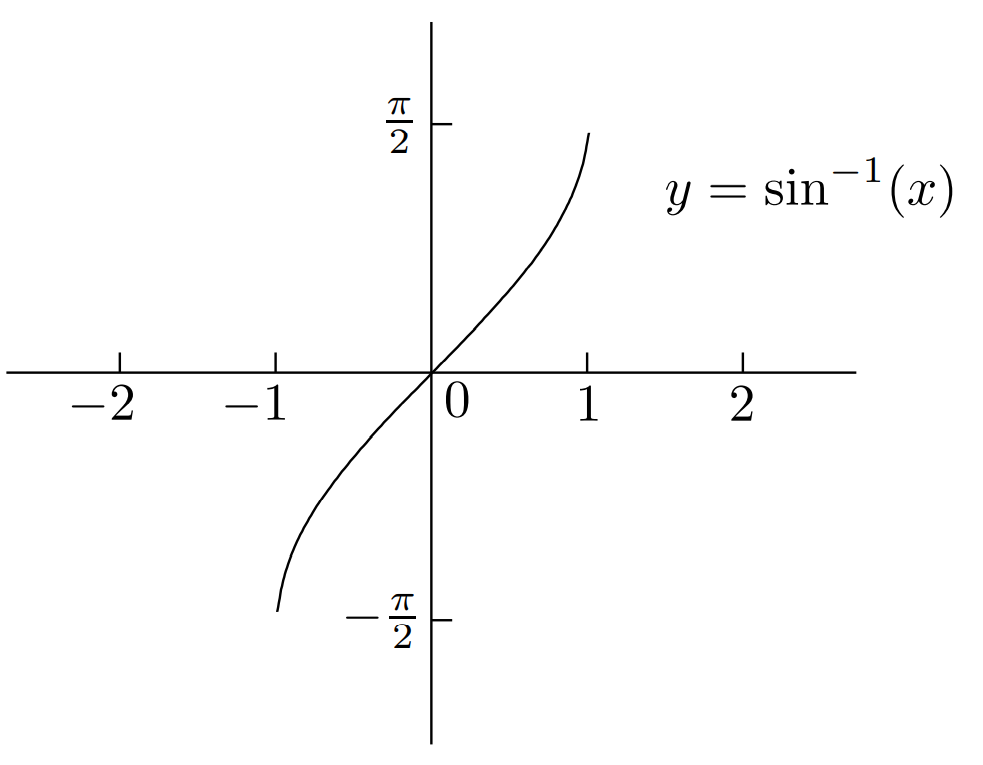
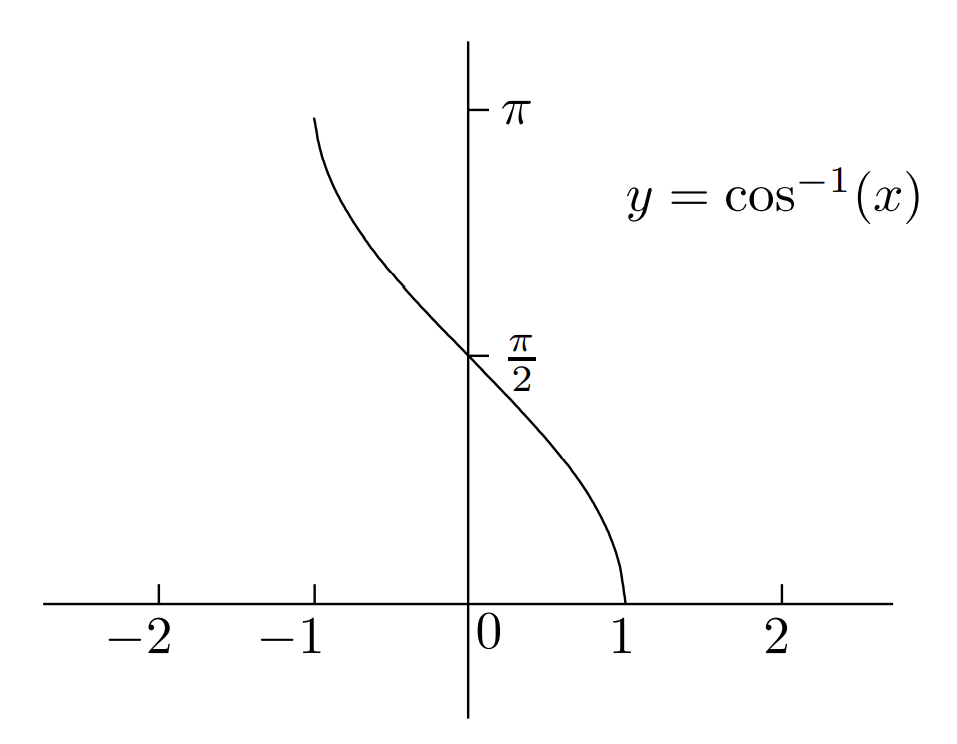
重要关系
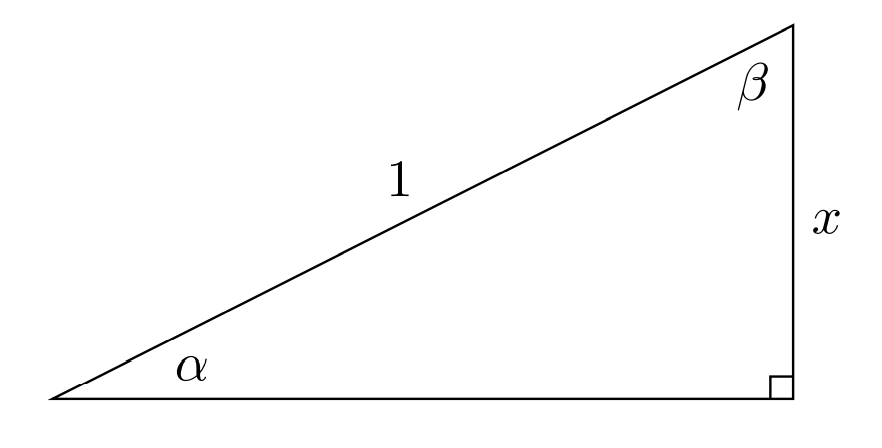
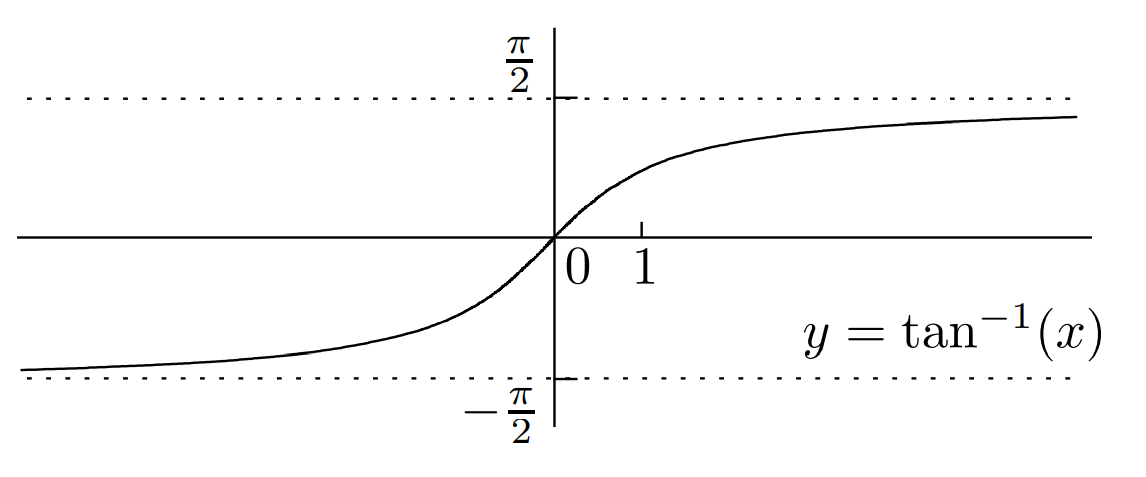
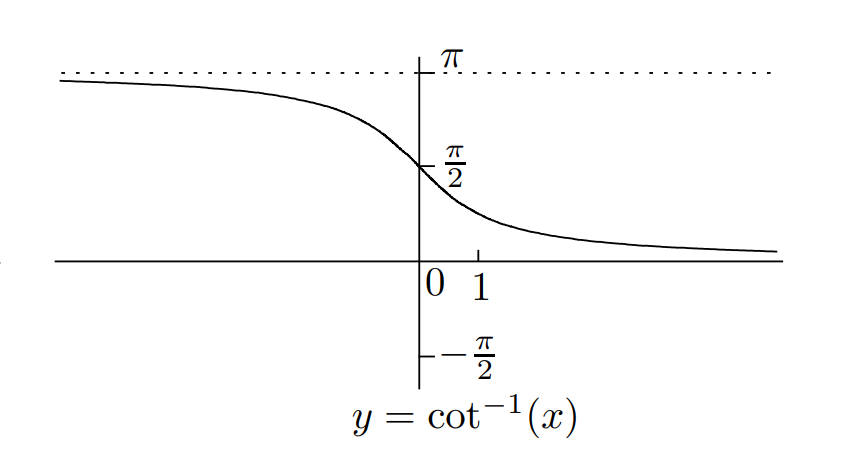
例
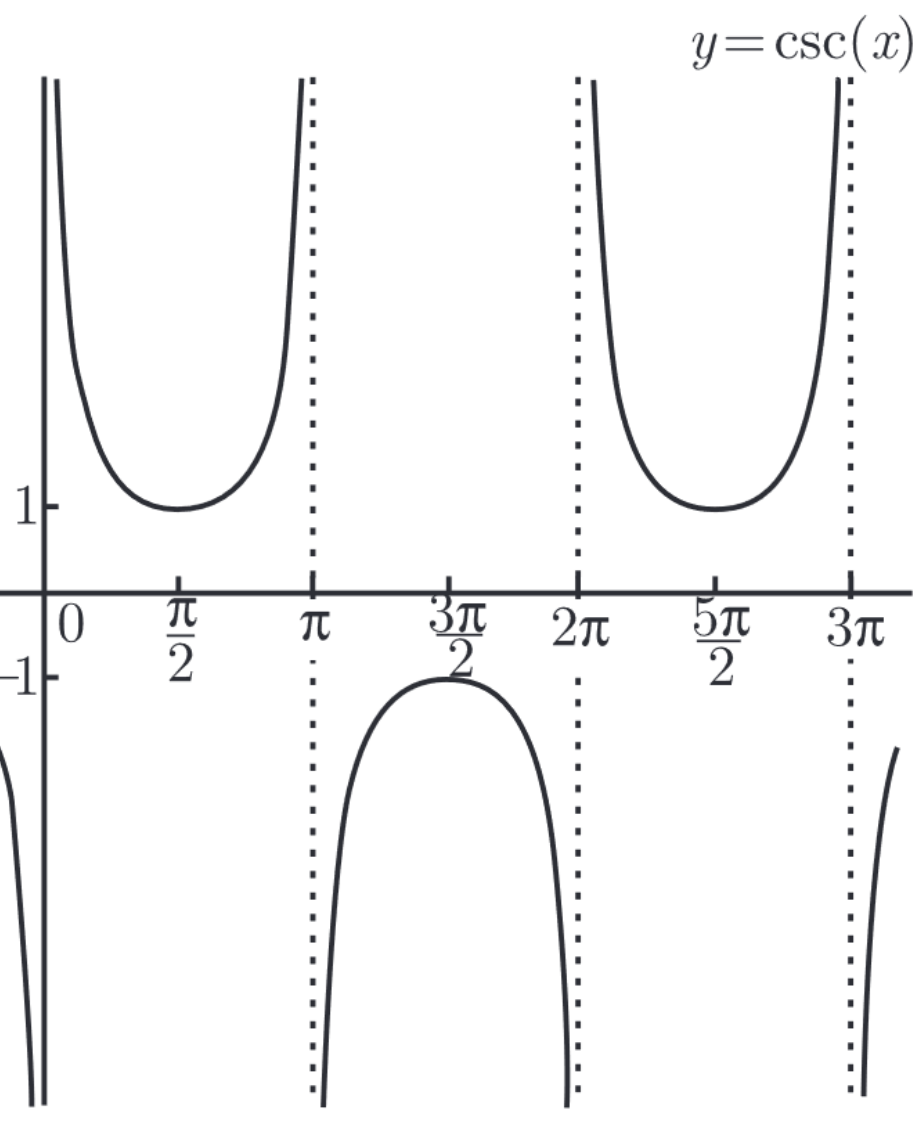
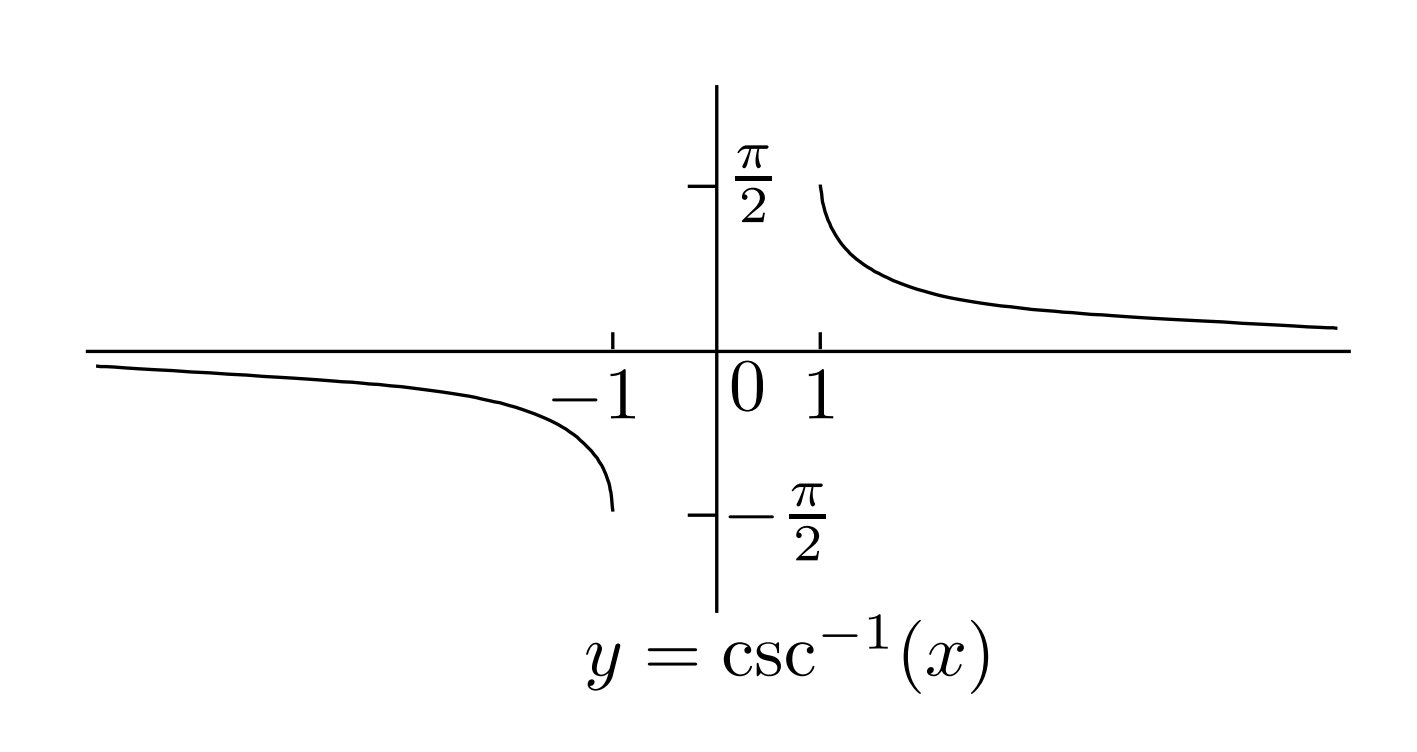
双曲函数
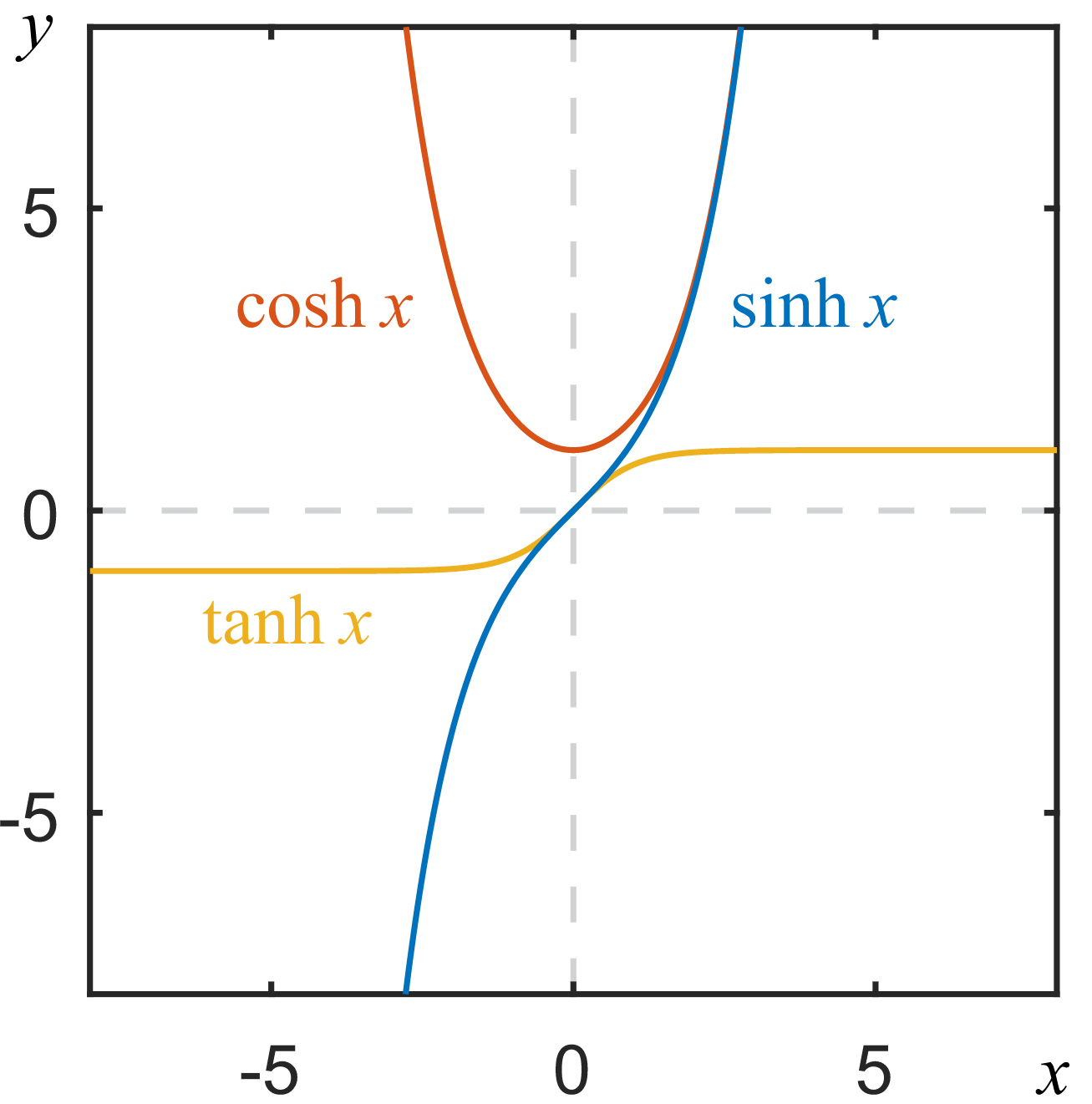
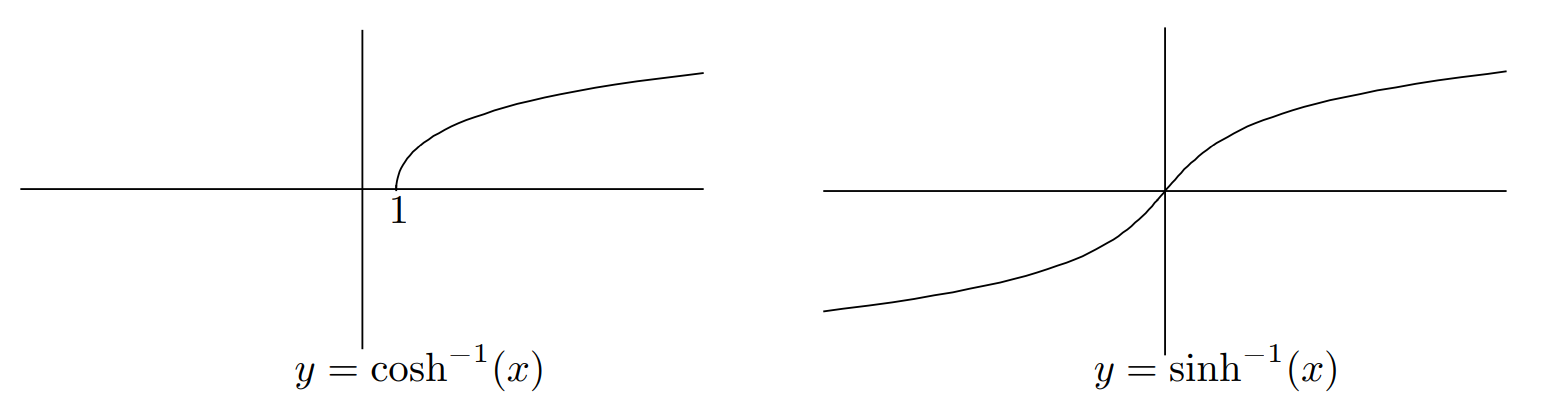
函数的极限
$\varepsilon-\delta$定义
$\forall \varepsilon>0$,$\exists \delta>0$,使得$x\in(a-\delta,a+\delta)$时,$|f(x)-A|<\varepsilon$恒成立,但存在$f(a)$无定义,故$0<|x-a|<\delta$
记作:
去心$\delta$邻域
右$\delta$邻域
左右极限
若对$\forall \varepsilon>0$,$\exists \delta>0$,当$x\in\mathring{U}^+(a,\delta)$时恒有${|f(a)-A|<\varepsilon}$
就称$A$为函数$f(x)$在$a$处的右极限,记为
定理
无穷
设$f(x)$在$|x|>M,M>0$时有定义,$A$为某一常数,若对任意$\varepsilon>$0,都$\exists X>0$使得当$ |x|>X$时
那么就称$A$为函数$f(x)$当$x\to \infty$的极限
同理正无穷去掉绝对值
性质
有界性
设$f(x)$在区间$X$上有定义,且对任意$x\in X$,存在$M$使得
就称$f(x)$在$X$上有界
同理若
则称$f(x)$在X上有上界,其中$K_1$为$f(x)$在$X$上的一个上界
连续
$f(x)\in C[a,b]$则$f(x)$在$[a,b]$上有界
但开区间不一定满足有界
若有界则$\exists \lim{x\to a^+} f(x),\lim{x\to b^-} f(x)$
极限的性质
唯一性
若有极限,则必唯一
逆否:若左右极限不等,则极限不存在
局部有界性
函数与数列的区别是函数是连续的而数列是离散的
如$y=\frac1x$极限为$0$但无界
若$\displaystyle\lim_{x\to a}f(x)=A$,则$\exists \delta>0$,当$x\in \mathring{U}(a,\delta),|f(x)|\le M(M>0)$
反向
若$\displaystyle\lim_{x\to a}f(x)=A(A\ne 0)$,则$\exists \delta>0$,当$x\in \mathring{U}(a,\delta),|f(x)|>\left|\frac A2\right |(M>0)$
单侧有界性
可单侧使用
若右极限存在,则在右邻域中有界
保号性
若$\displaystyle\lim_{x\to a}f(x)=A>0$,则$\exists \delta>0$,当$x\in \mathring{U}(a,\delta),f(x)>0$
复合函数
$y=f[\varphi(x)]$==其中$\varphi (x)\ne a $==,若
$f(x)$可能在$a$处无定义
连续与间断
定义,若$f(x)$在$x_0$的邻域(不去心)有定义,且
等价定义(三合一),必须双向逼近
特点:
- 在邻域有定义$\exists f(x_0)$
- 左右极限存在且相等
- 等于函数值
在区间上连续
开区间若每一点连续则在区间上连续
闭区间在端点处只要求单侧连续
基本初等函数在定义域上连续
初等函数在定义区间上连续($\text{not}$定义域)
反例$y=\sqrt{\sin x-1}$无邻域
运算
四则注意分母不为0
复合函数
内层不需要连续,连续则极限符号可交换
间断
首先有函数在去心领域有定义,其次不连续
介值定理
$f(x)$在$[a,b]$上连续,则对$\forall c\in[m,M]$,$\exists \xi\in[a,b],\text{s.t.}f(\xi)=c$
离散形式
数列满足$|a{n+1}-a{n}|\le1$则类比介值定理
零点定理
$f(x)$在$[a,b]$上连续,则若$f(a)f(b)<0$,$\exists \xi\in(a,b),\text{s.t.}f(\xi)=0$
实际上为零点定理的特殊形式
特殊函数
绝对值$|x|$,$0$处连续但不可导
曲线光滑不一定可导
$y=x^{\frac13},y’=\frac{1}{3x^{\frac23}},x\to0,y’=\infty$
导数存在不一定连续可导(导函数连续)
符号函数
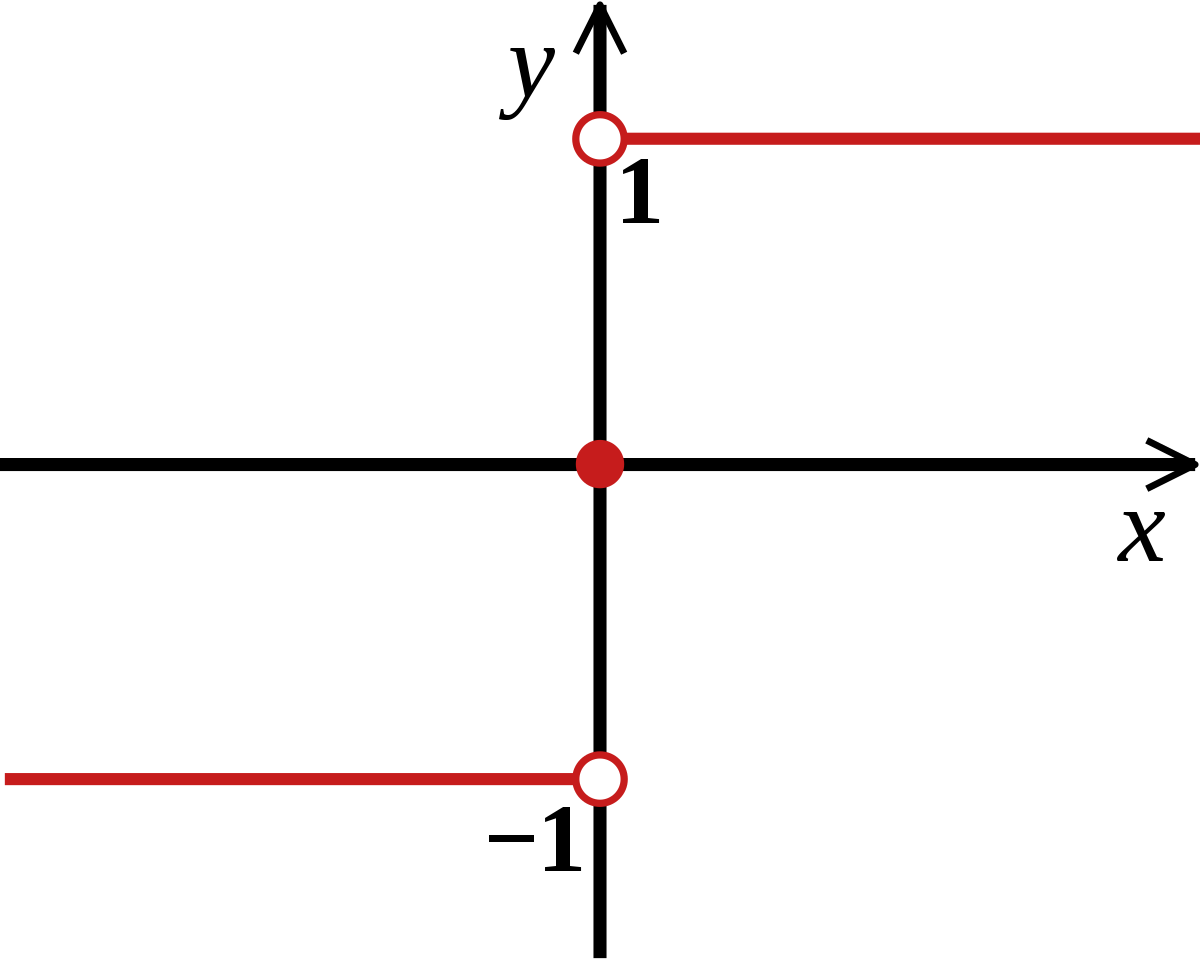
$|f(x)|$连续
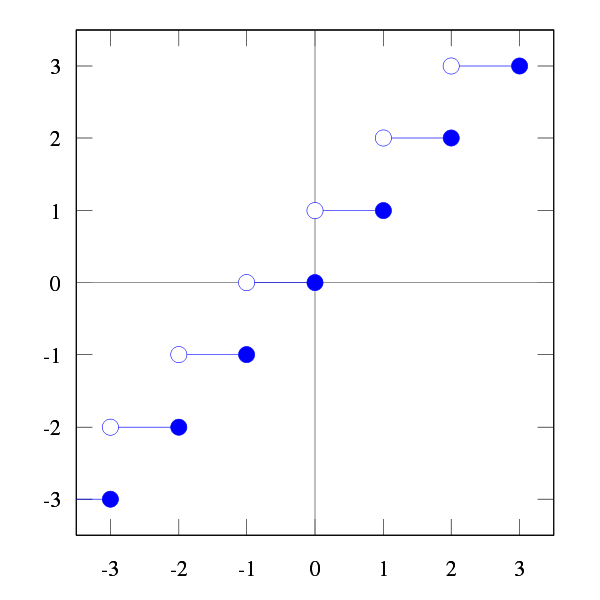
定义域为$\mathbf R$,值域为$\mathbf Z$
Dirichlet function
处处无极限,处处不连续,处处不可导
任意有理数都为其周期,无最小正周期,偶函数