高中/芳贺定理

1.芳贺第一定理

日本筑波大学生物学教授芳贺和夫（Kazuo Haga），在等待实验结果的时候喜欢用摺纸打发时间。他发现了以下的有趣结果。

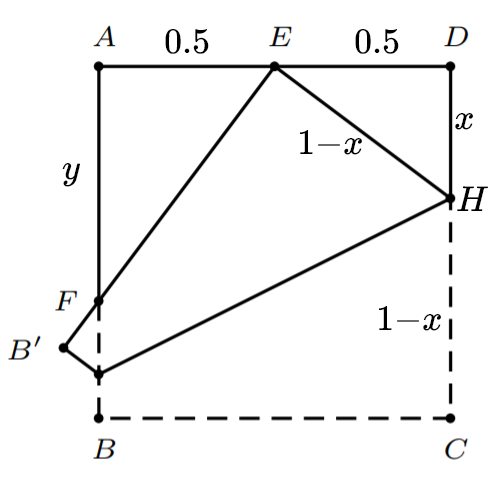
$Claim:F$为$AB$的三等分点

$proof:$

设正方形边长为1，将$C$折到$AD$的中点$E$处，由图

$x^{2}+\left(\frac{1}{2}\right)^{2}=(1-x)^{2}$

解得$x=\frac{3}{8}$

又$\triangle FAR \sim \triangle EDH$

$\frac{y}{\frac{1}{2}}=\frac{\frac{1}{2}}{x}$

解得$y=\frac{2}{3}$

$Property:$

推广：

$x^{2}+k^{2}=(1-x)^{2}$ $\frac{y}{1-k}=\frac{k}{x}$

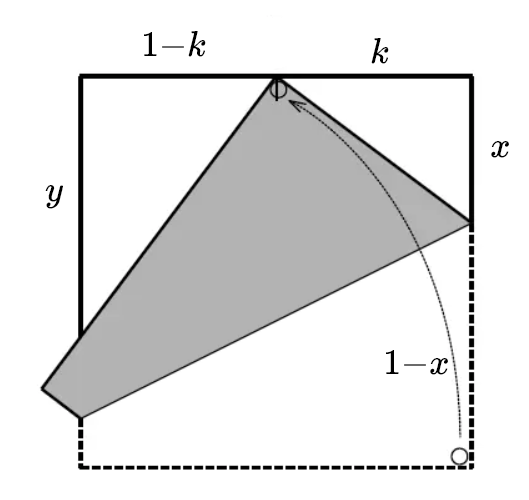
通过相似三角形和勾股定理，联立两个方程

$\frac{y}{1-k}=\frac{k}{\left(1-k^{2}\right) / 2}$ $\frac{y}{2}=\frac{k}{1+k}$

若正方形边长为1，有$k=\frac{1}{N}$，带入得到

$\frac{y}{2}=\frac{1 / N}{1+1 / N}=\frac{1}{N+1}$

如果一直按此方法重复，就可以由$n$等分得到$n+1$等分，于是便得到了任意等分 ~~有点麻烦~~

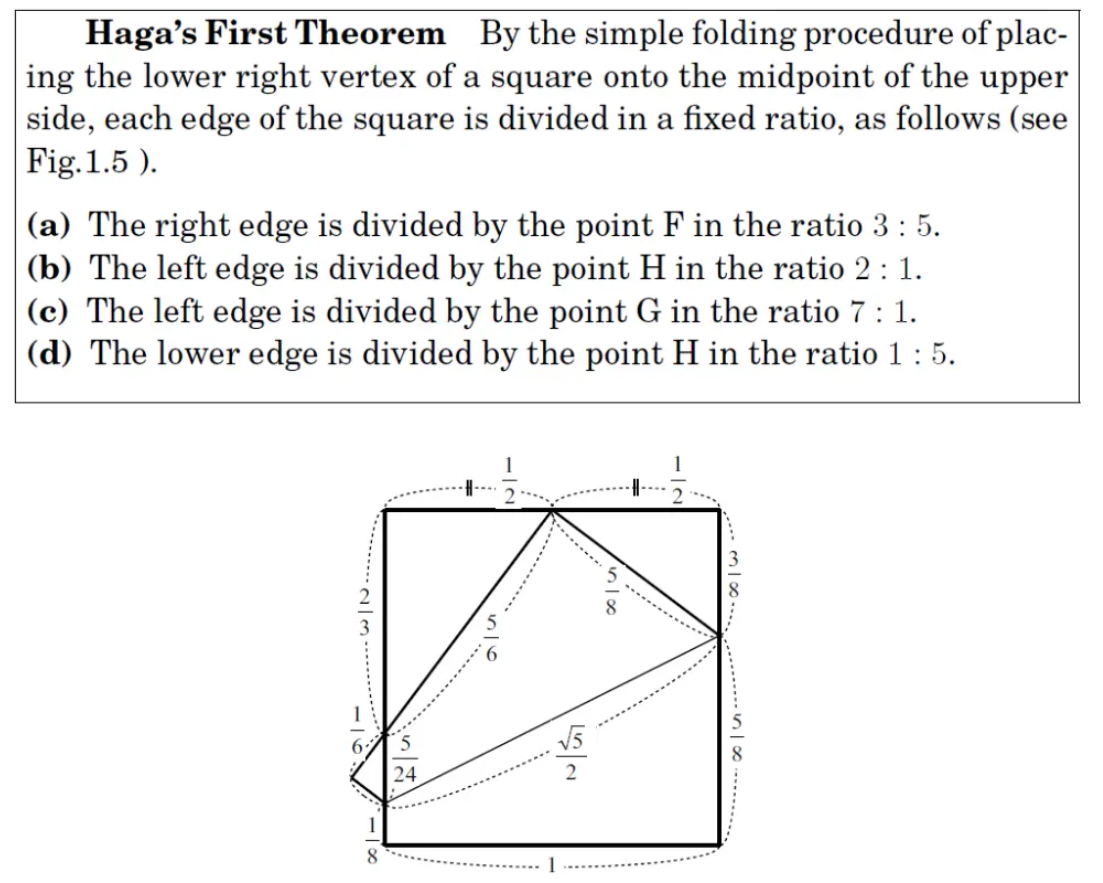注意左上角的直角三角形，它是一个$3:4:5$的直角三角形，难道这只是巧合吗

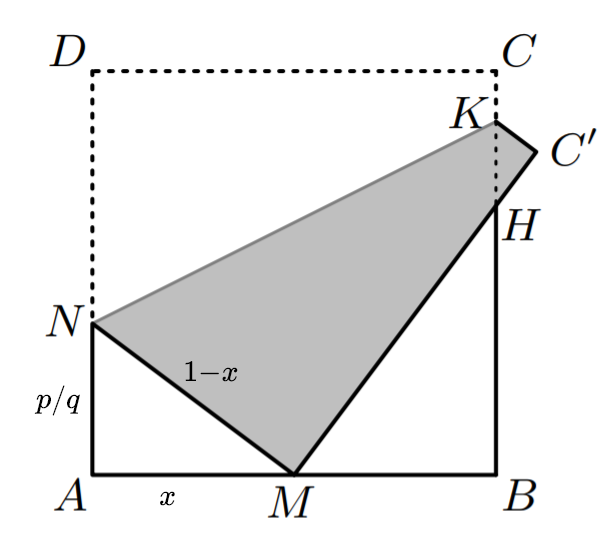
$A B=1, A N=x $及$A M=\frac{p}{q} $其中 $p, q \in \mathbb{N}, M N=1-x $

$\begin{aligned} \left(\frac{p}{q}\right)^{2}+x^{2} &=(1-x)^{2} \\ \frac{p^{2}}{q^{2}}+x^{2} &=1-2 x+x^{2} \\ x &=\frac{q^{2}-p^{2}}{2 q^{2}} \end{aligned}$

所以，

$\begin{aligned} A N: A M: M N &=\frac{q^{2}-p^{2}}{2 q^{2}}: \frac{p}{q}: 1-\frac{q^{2}-p^{2}}{2 q^{2}} \\ &=q^{2}-p^{2}: 2 p q: p^{2}+q^{2} \end{aligned}$

所以只要$p$和$q$是整数，那么这三条边的比就一定是勾股数

$\begin{array}{|l|l|} \hline p / q & A N: A M: M N \\ \hline 1 / 2 & 3: 4: 5 \\ \hline 2 / 3 & 5: 12: 13 \\ \hline 1 / 4 & 15: 8: 17 \\ \hline \end{array}$

2.芳贺第二定理

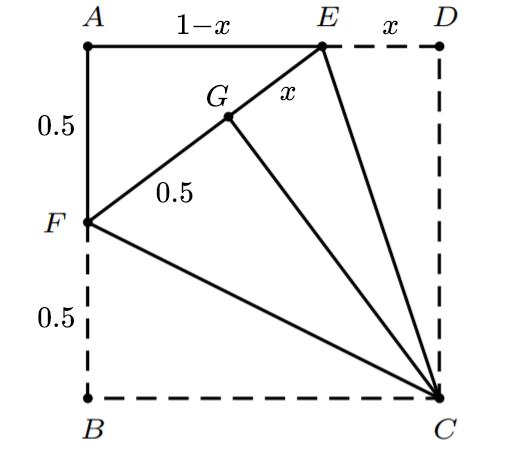
将$AB$沿$CF$折叠，延长$FG$交$AD$于$E$

在$\triangle AEF$中，有

$(1-x)^{2}+(\frac{1}{2})^{2}=(x+\frac{1}{2})^2$

解得$x=\frac{1}{3}$，即$E$是$AD$的三等分点

3.芳贺第三定理

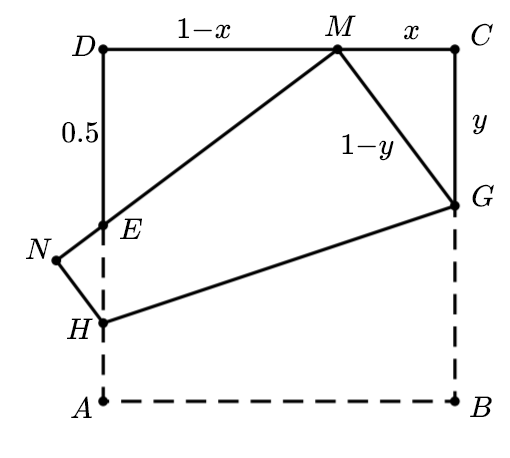
设正方形 $ABCD$的边长为1,$ C M$=$x$, $C G$=$y$

将$AB$边折到$AD$中点$E$上，并让$B$点落在$CD$上

由 $\triangle E D M \sim \triangle C M G$, 可得

$\frac{D E}{D M}=\frac{C M}{C G}$

在$\triangle C M G$ 中, $G M $=$ 1-CG=1-y$，有

$x^{2}+y^{2}=(1-y)^{2}$

解之得

$y=\frac{1-x^{2}}{2}$

带入得$x=\frac{1}{3}$，即点$M$是$ C D $的三等分点.

4.再谈n等分

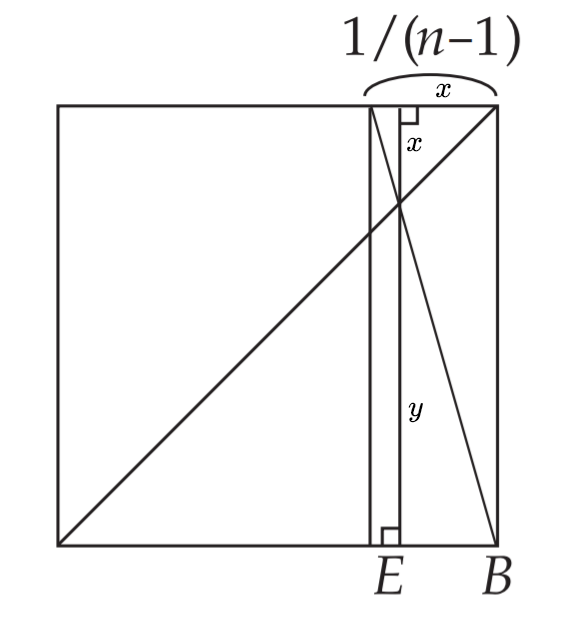
如果我们得到了$n-1$等分，在图中不难看出

$\frac{\frac{1}{n-1}}{1}=\frac{x}{y}$

消去$y$可以得到$x=\frac{1}{n}$

这样我们又有一种n等分的方式

$tip:$如果要得到7等分，我们可以先折3等分再对折，从而由6等分得到7等分

1.芳贺第一定理

推广：

2.芳贺第二定理

3.芳贺第三定理

4.再谈n等分

References: