解析几何
椭圆
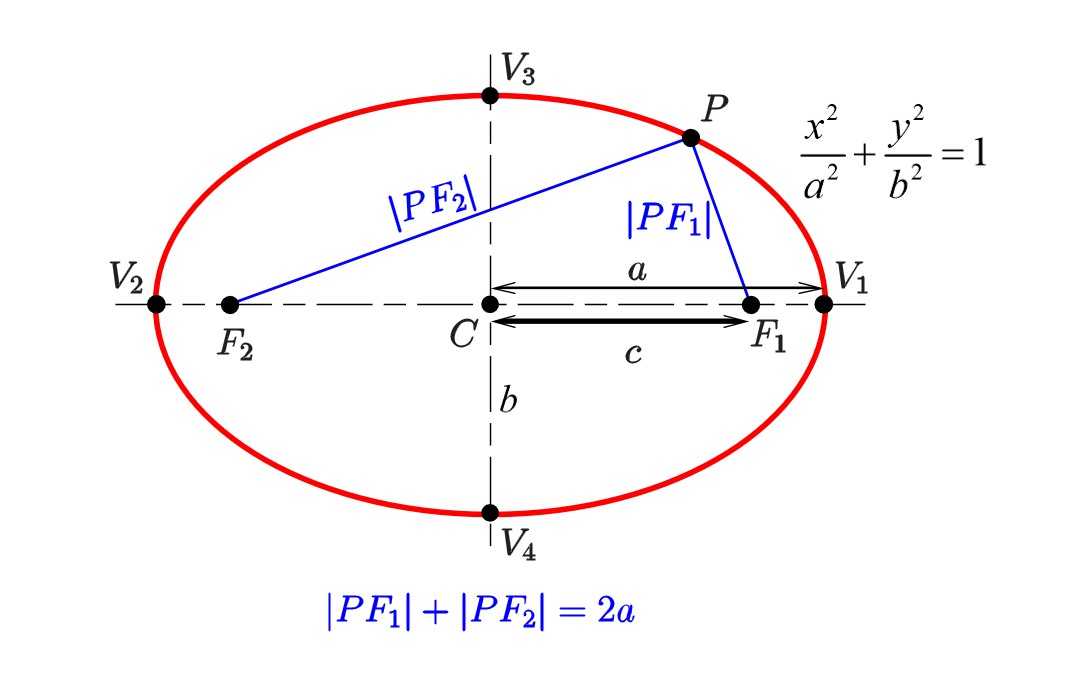
第一定义
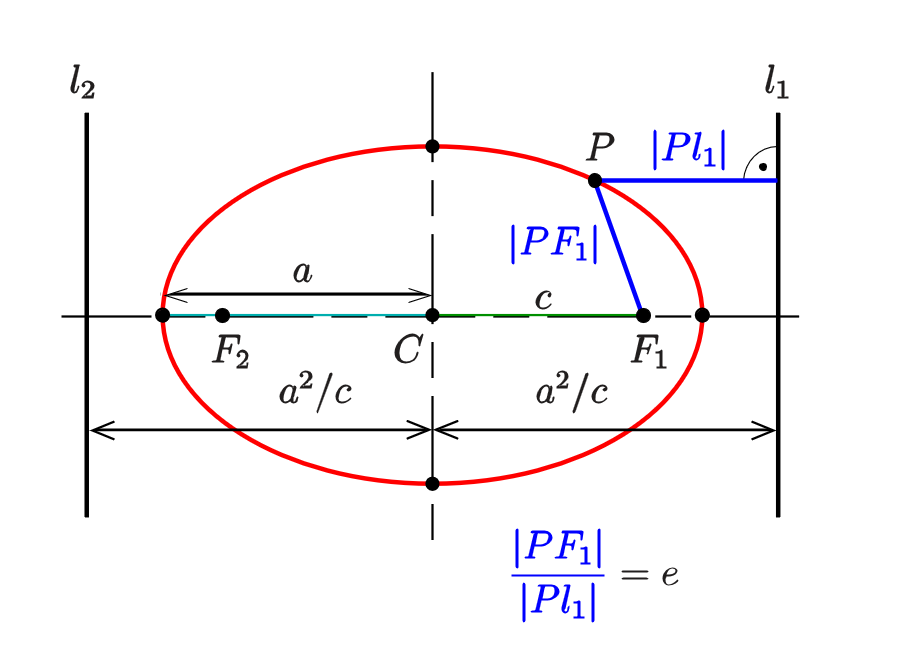
第二定义
第三定义
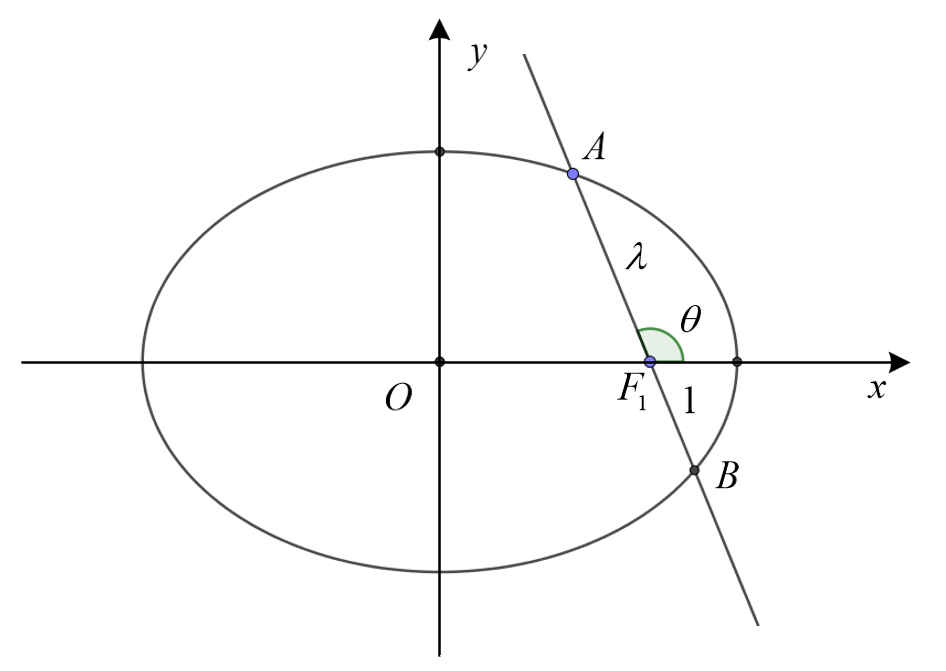
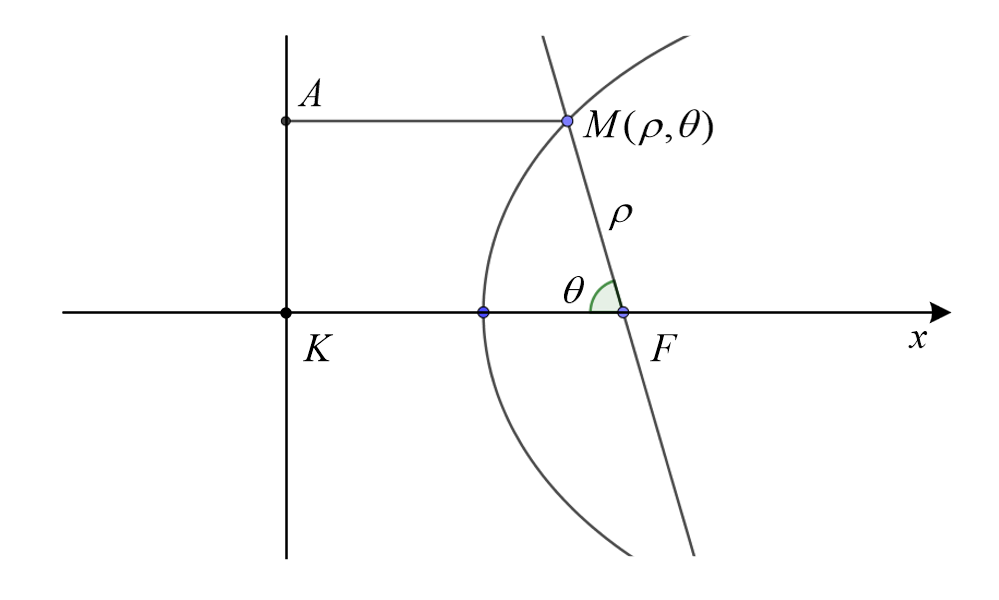
极坐标
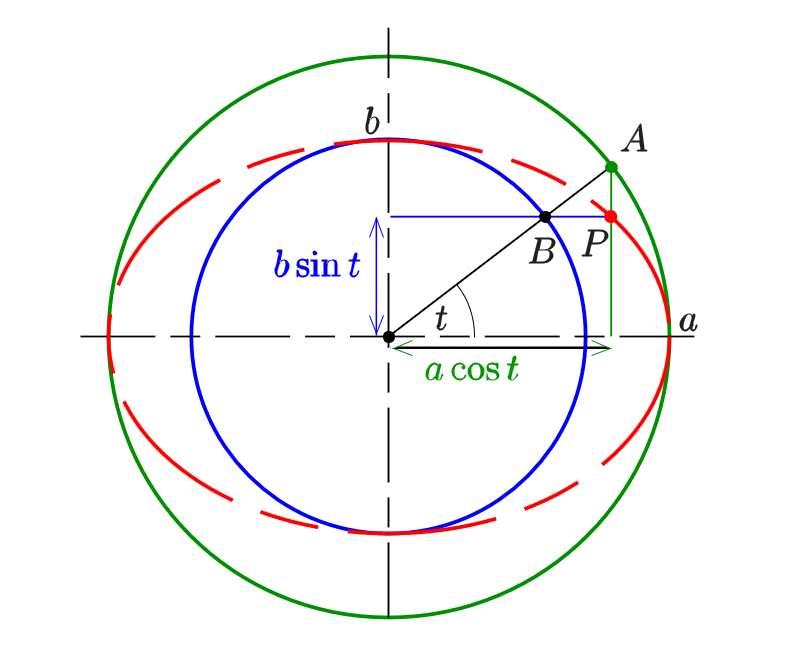
参数方程
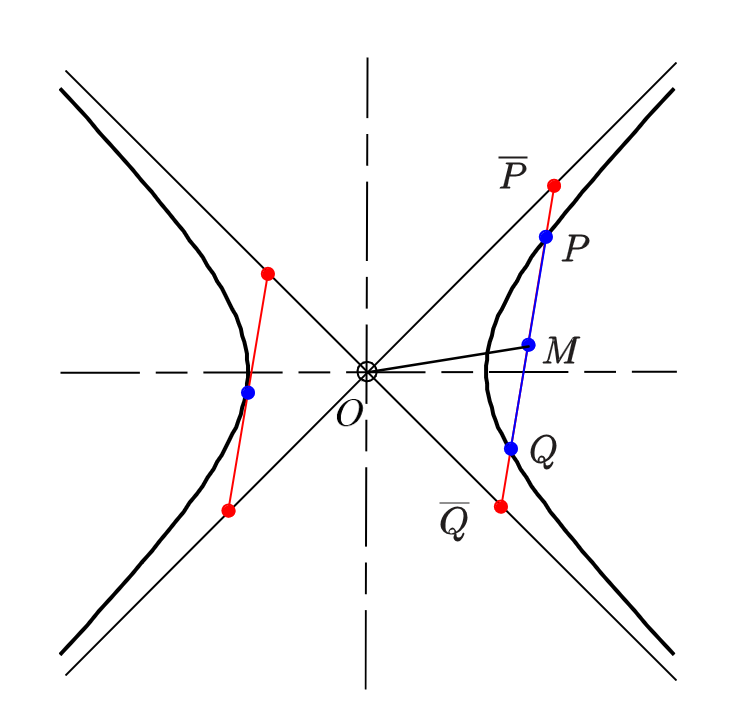
双曲线
第一定义
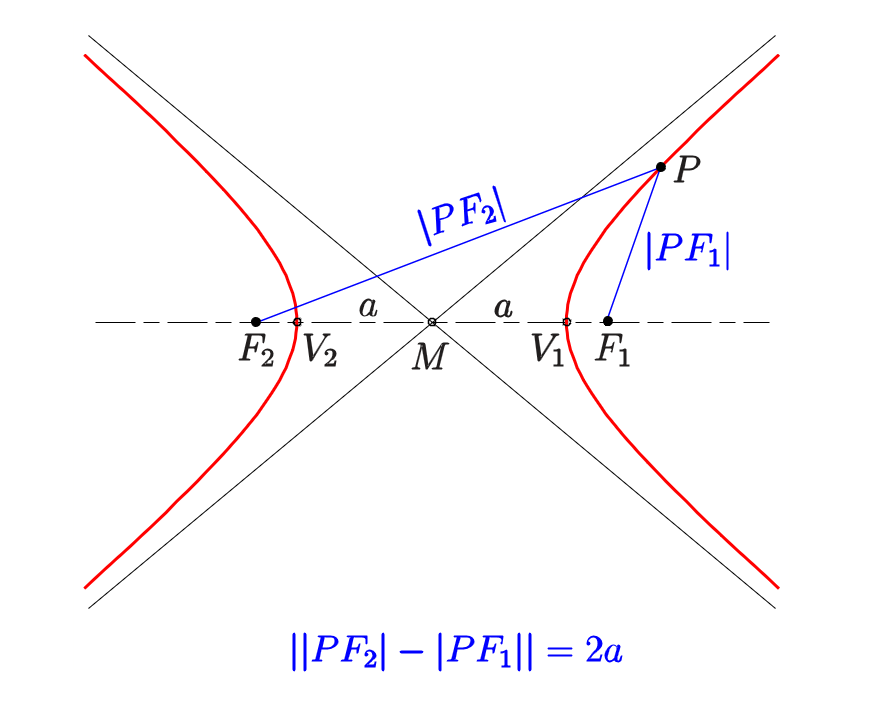
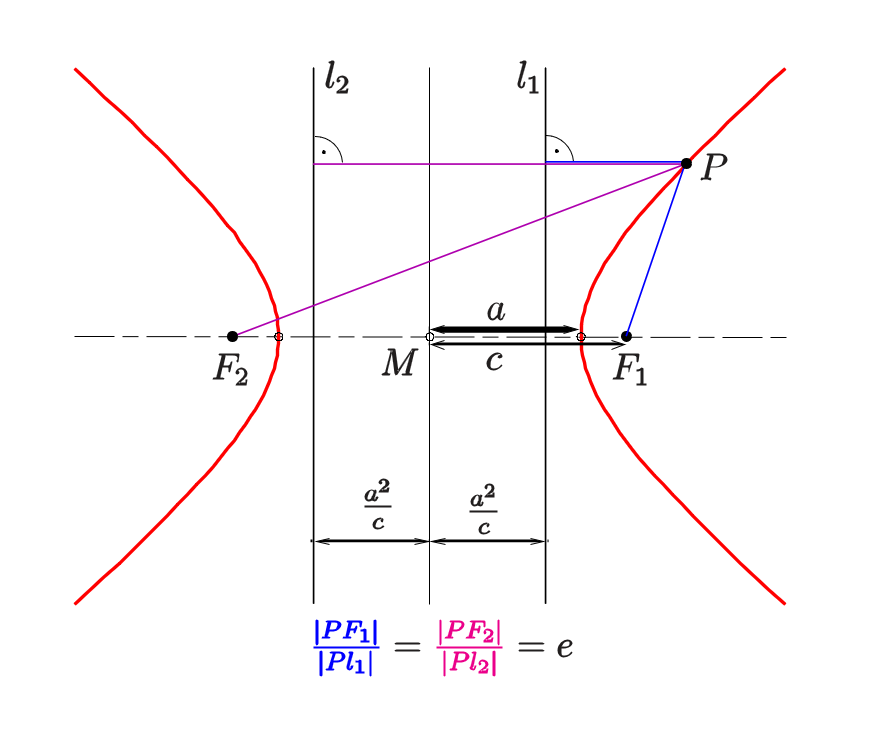
第二定义
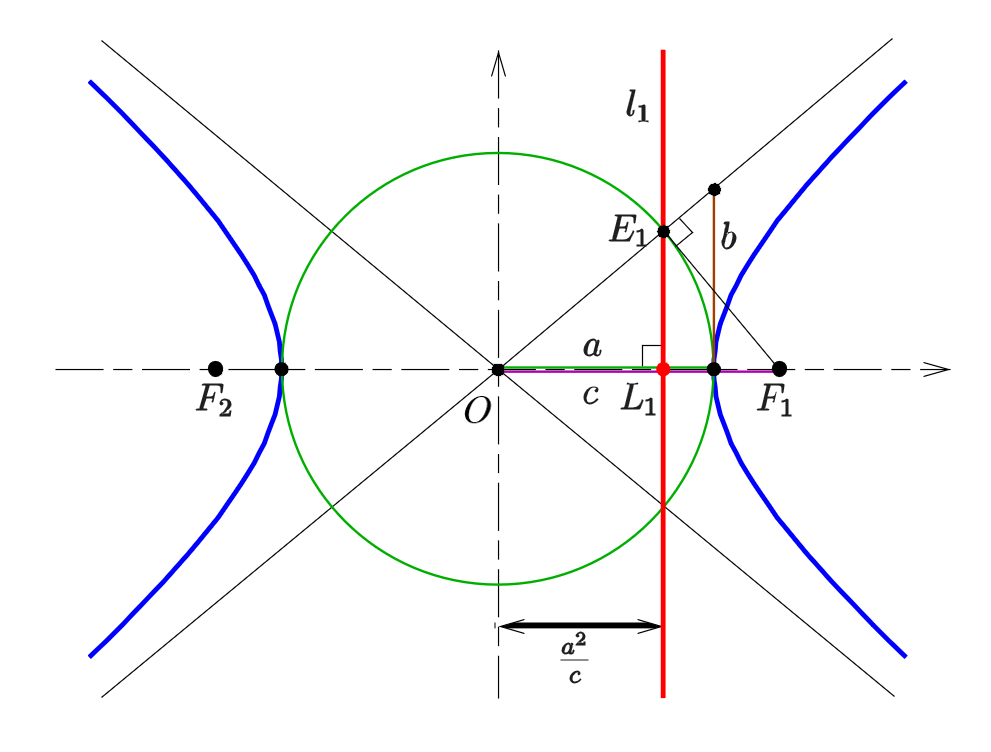
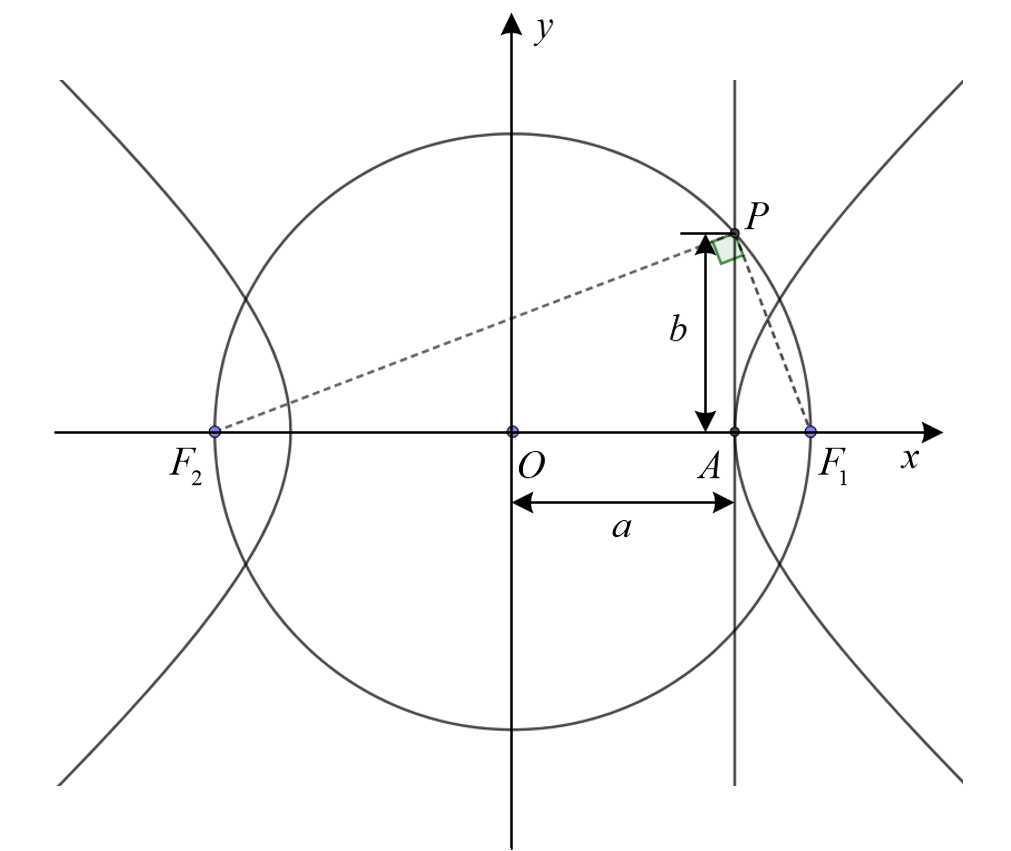
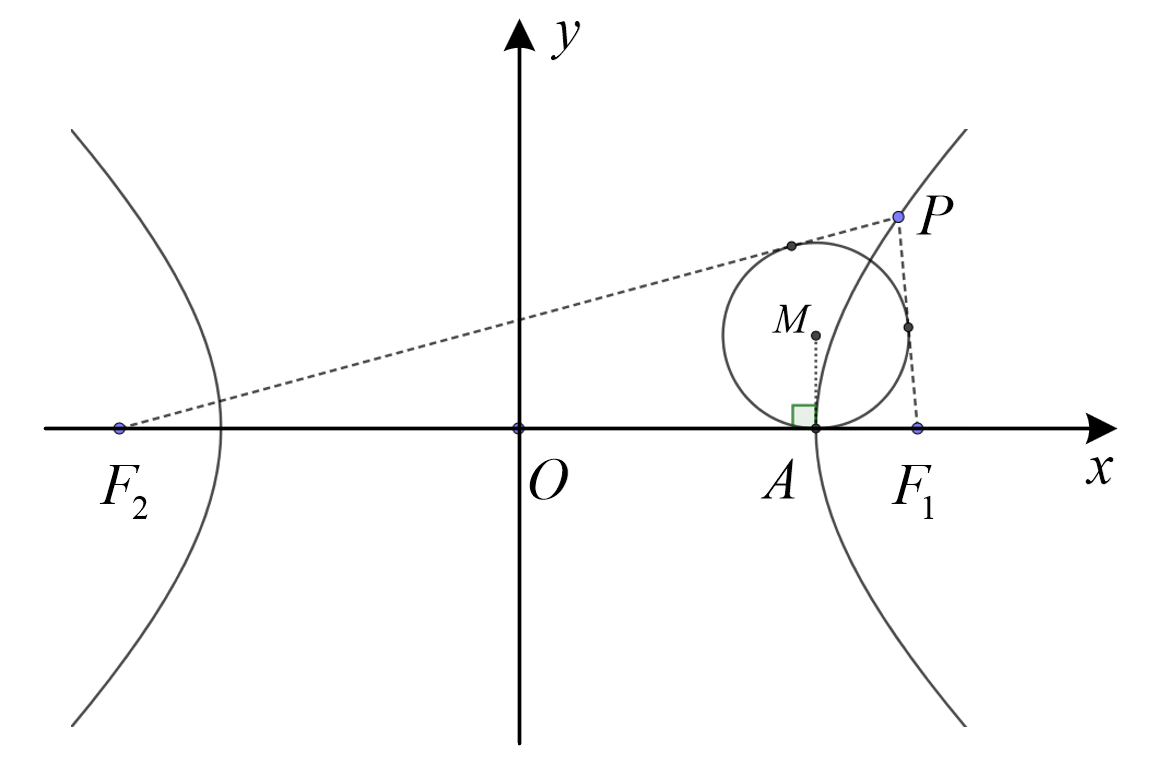
性质
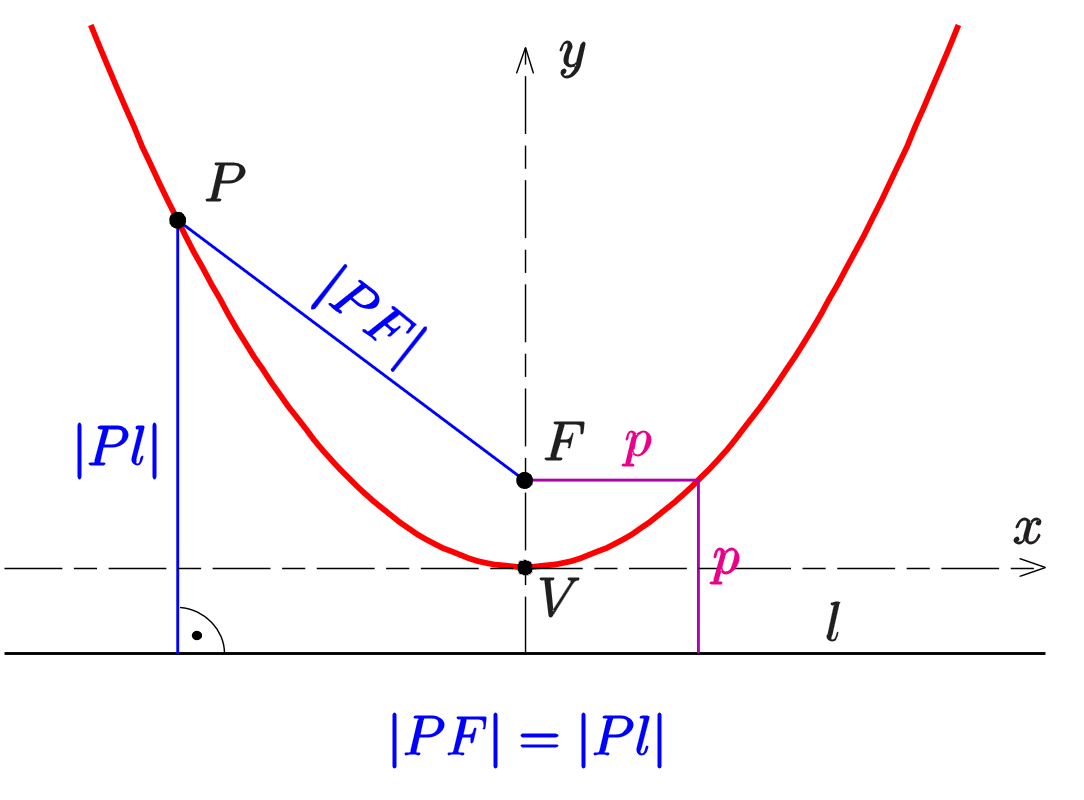
抛物线
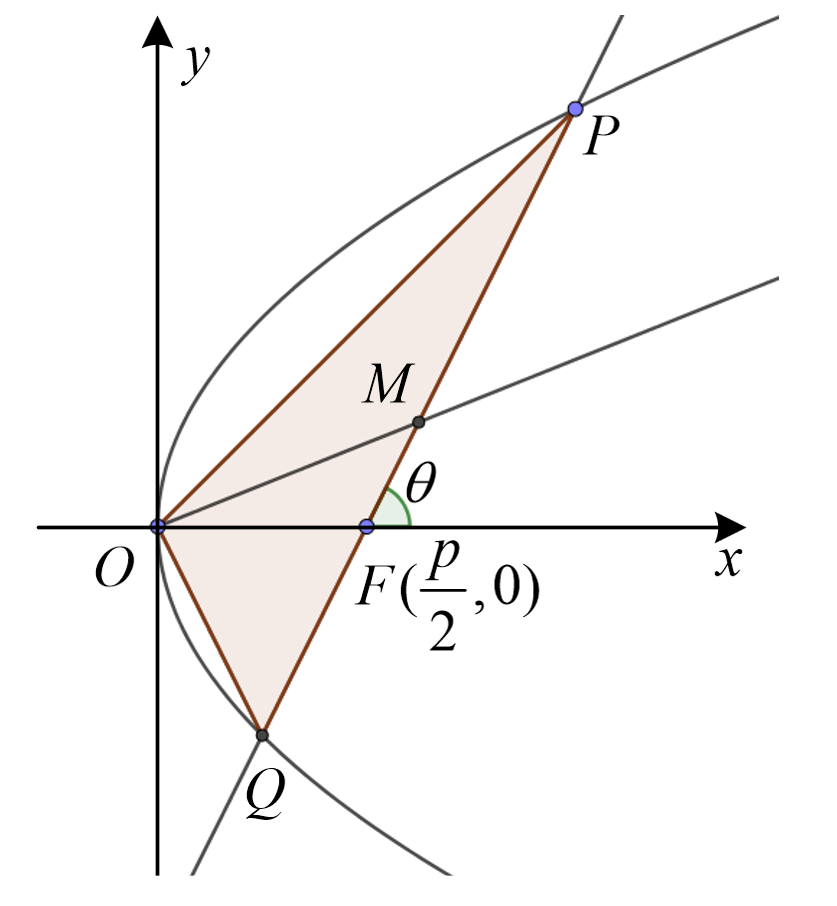
焦点弦
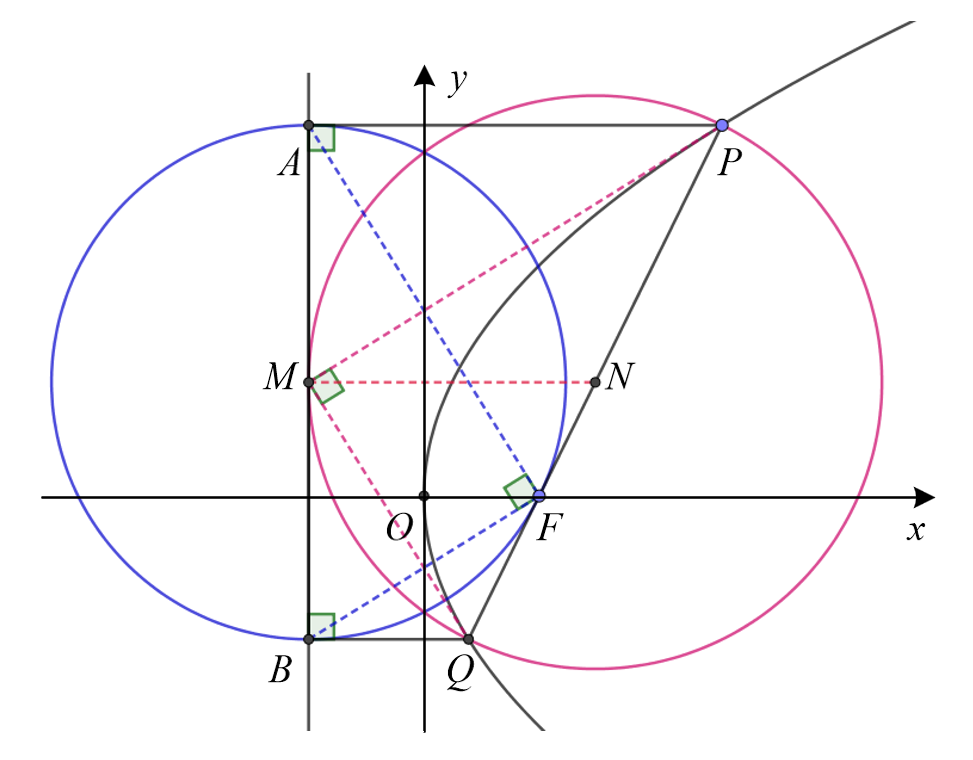
参数方程
切线
切线方程为
抛物线
双曲线
椭圆切线
双曲线切线
不包括斜率不存在时
$P({x_0},{y_0})$在切线上,解出$k$
若$k^2$前系数为$0$,则为一次方程,有一条斜率存在的切线,还有一条不存在的切线
若$k^2$前的系数不为$0$,则该方程是一个关于$k$的一元二次方程,可能有$0$个,$1$个,$2$个解
若$\frac{x_0^2}{a^2} - \frac{y_0^2}{b^2}=0$,有一根为$k=\frac{b}{a}/ - \frac{b}{a}$,故舍去