5.抛物线折叠
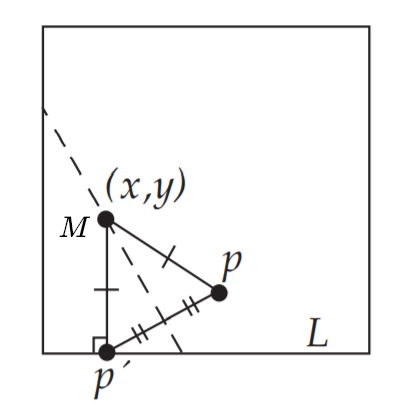
取一张纸,将边线当做线$L$,在纸上取点$P$,将$P$折叠到$L$上,对应点为$P’$,压出折痕,如下图所示
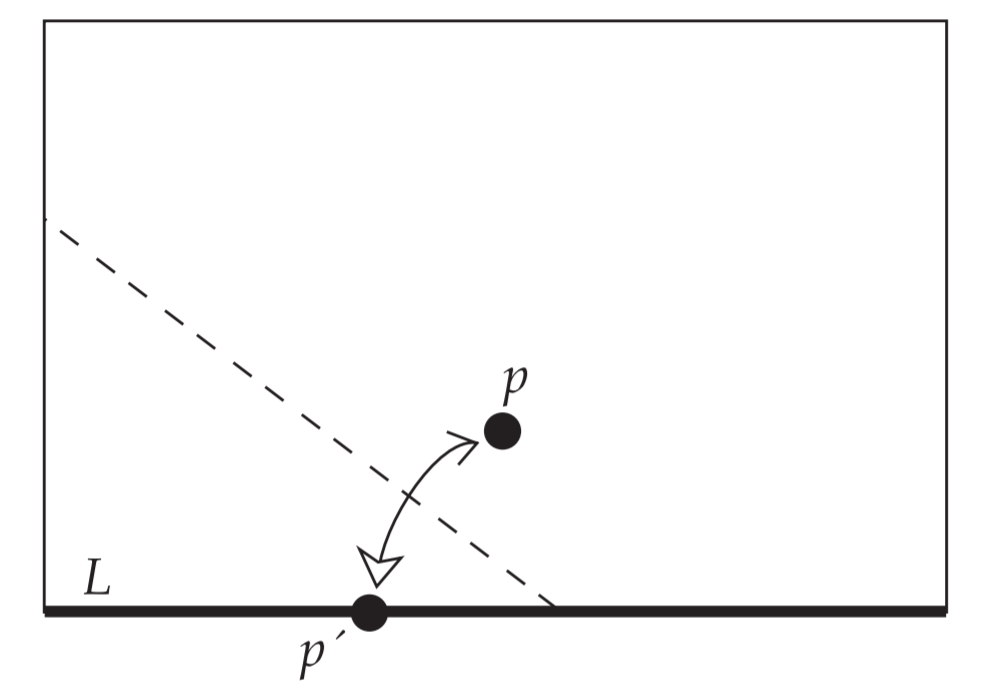
观察折痕所形成的图形
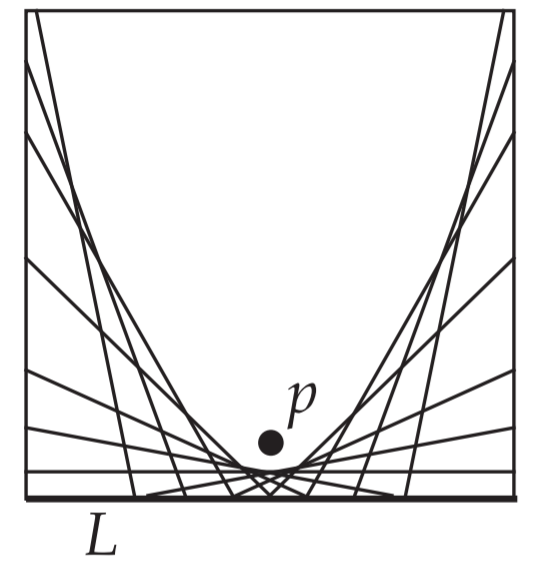
看上去像是一条抛物线,但我们需要严格证明
分析:
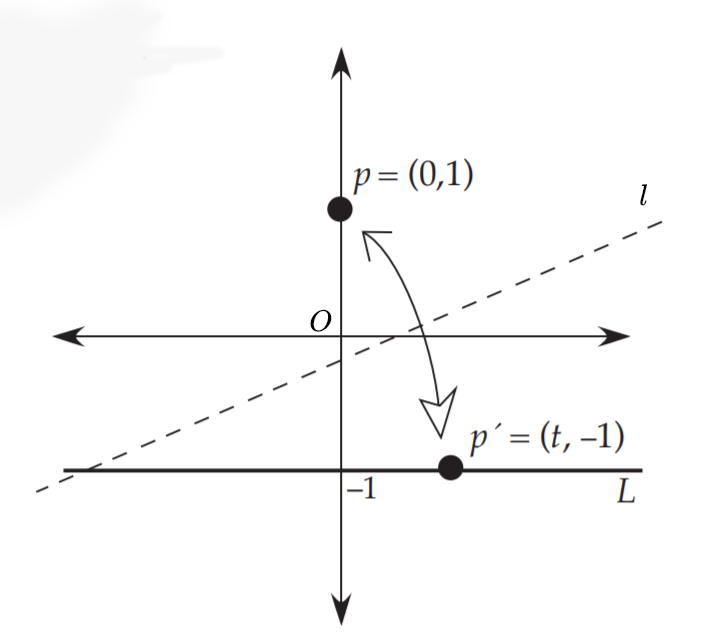
以$O$为原点建立坐标系,使得$p$点坐标为$(0,1)$,$p’$点的坐标为$(t,1)$,下面求折线的方程
因为折线$l$是$pp’$的中垂线
$\left. { k{pp^ { \prime }} = \frac { 2 } { t } } \ { k { l } = \frac { t } { 2 } } \ { y - 0 = \frac { t } { 2 } ( x - \frac { t } { 2 } ) } \ { y = \frac { t } { 2 } x - \frac { t ^ { 2 } } { 4 } } \right.$
这就是折线的方程
求解抛物线方程
带入法:
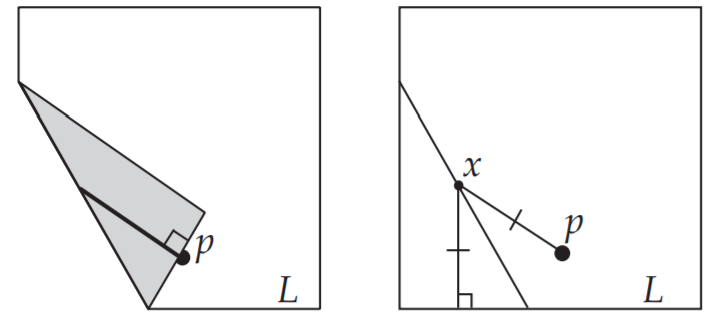
考虑折线上横坐标为$t$的一点$M$
将$t=x$代入折线方程
$y = \frac { x } { 2 } \cdot x - \frac { x ^ { 2 } } { 4 } = \frac { x ^ { 2 } } { 4 }$
这就是当$p’$在$L$上运动时,点$M$的轨迹方程
切线法:
折线即为抛物线的切线
$\frac{d y}{d x}=\frac{x}{2}$
两边积分得
$y=\frac{x^{2}}{4}+C$
又当$p’=(0,-1)$时,函数过$O=(0,0)$,故$C=0$,即
$y=\frac{x^{2}}{4}$
包络线法:
将折线方程化成有三个变量的隐式方程
$\left. { 4 y = 2 t x - t ^ { 2 } } \ { t ^ { 2 } - 2 t x + 4 y = 0 } \ { F ( x , y , t ) = t ^ { 2 } - 2 t x + 4 y } \right.$
带入包络线线上方一点$(0,1)$
$F ( 0,1 , t ) = t ^ { 2 } - 0 + 4 > 0$
故图像被分为两个区域
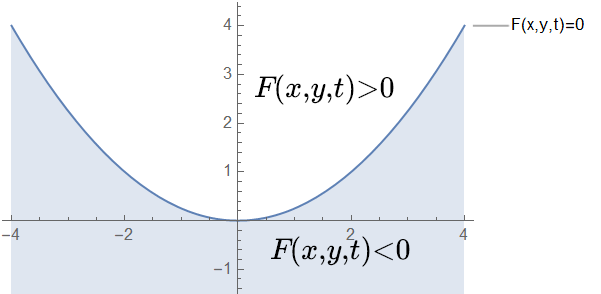
这个关系是对任意的$t$都成立
考虑包络线上一点$(x_0,y_0)$,仅存在一个$t$使得$F(x_0,y_0, t)=0$,对其余$t$的题都有$F(x_0,y_0, t)>0$
所以$F(x_0,y_0, t)$对$t$有极值,又因为$(x_0,y_0)$必须在折线上,故
$\left{ \begin{array}{lr} F(x, y, t)=0 \ \frac{\partial}{\partial t} F(x, y, t)=0\end{array} \right.$
$\frac{\partial}{\partial t} F(x, y, t)=2 t - 2 x=0$
解得
$t=x$
将$t=x$代入隐式方程,同样得到
$y = \frac { x } { 2 } \cdot x - \frac { x ^ { 2 } } { 4 } = \frac { x ^ { 2 } } { 4 }$
More examples
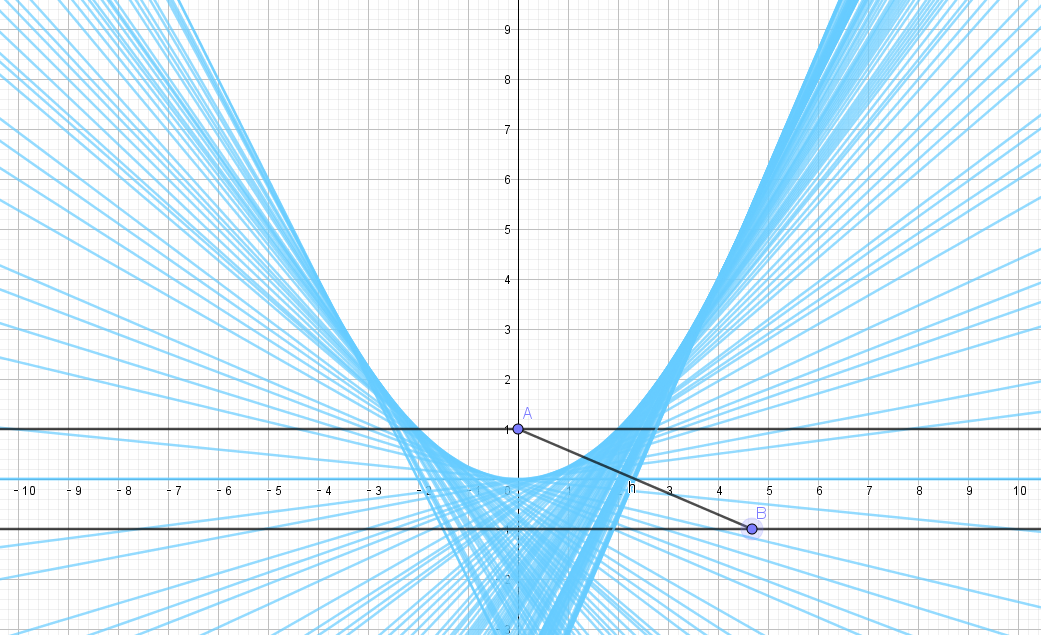

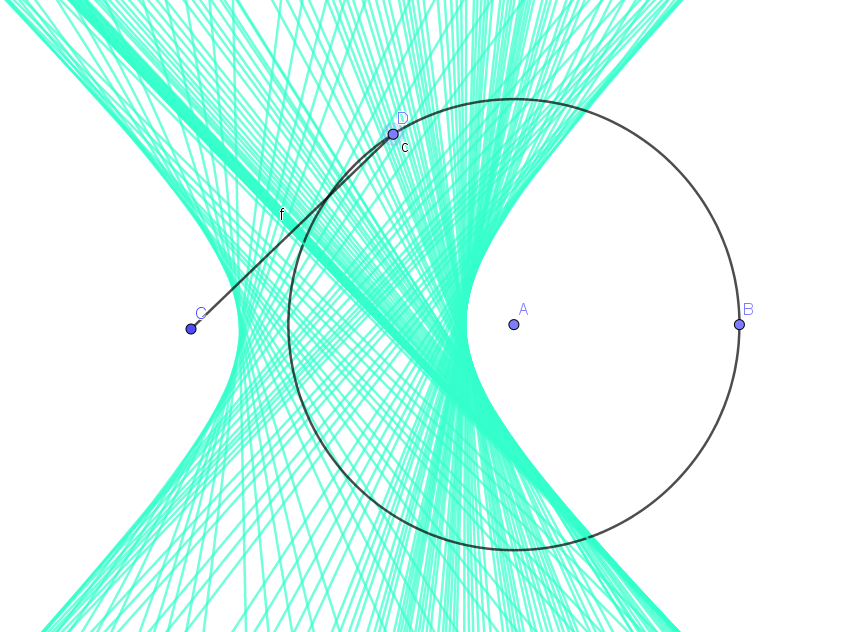
斜抛运动包络线:
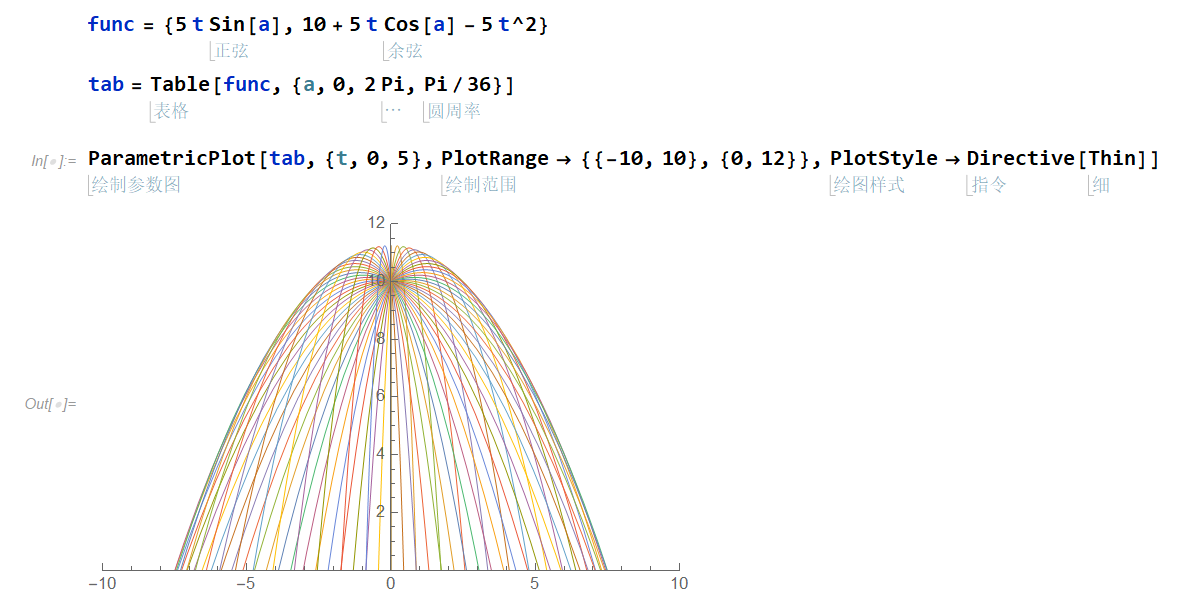

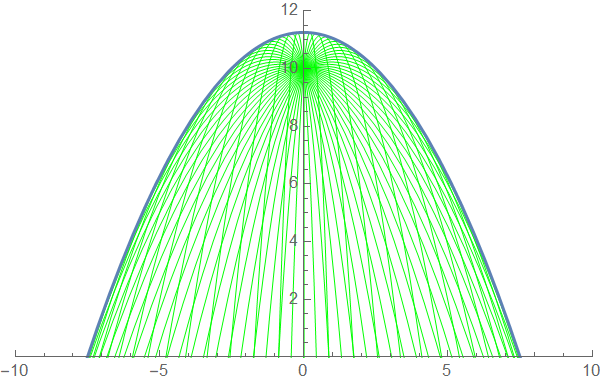
性质

重新观察这张图,$\frac{Mp}{Mp^{\prime}}=e=1$,根据抛物线的第二定义
将$p$到$L$上所形成的折线便是以$p$为焦点,以$L$为准线的抛物线的一条切线,这个性质将在下一节中起到非常重要的作用。