川崎定理(The Kawasaki-Justin Theorem)
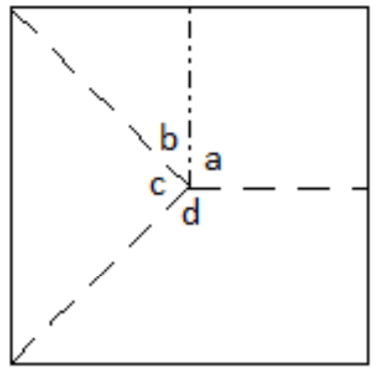
$a=90^{\circ}, b=45^{\circ}, c=90^{\circ}, d=135^{\circ}$
$a-b+c-d=90^{\circ}-45^{\circ}+90^{\circ}-135^{\circ}=0^{\circ}$
还是假设一只蚂蚁在纸上爬行
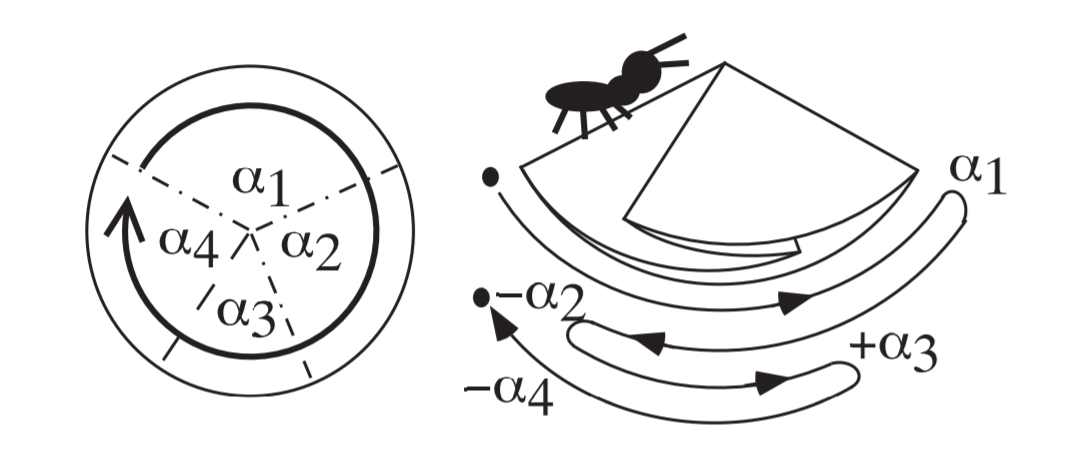
定义$\alpha{2n-1}>0$,$\alpha{2n}<0$
爬行一周过后,蚂蚁回到了原点,位移为0,即图中
$\alpha{1}-\alpha{2}+\alpha{3}-\alpha{4}=0$
由偶数定理,推广这个结论
$\alpha{1}-\alpha{2}+\alpha{3}-\cdots-\alpha{2 n}=0$
更简洁的表述为
$\sum(-1)^{i} \alpha_{i}=0$
$\because \sum \alpha_{i}=360^{\circ}$
$\therefore \alpha{1}+\alpha{3}+\cdots+\alpha{2 n-1}=\alpha{2}+\alpha{4}+\cdots+\alpha{2 n}=180^{\circ}$
局部最小定理(Local Min):
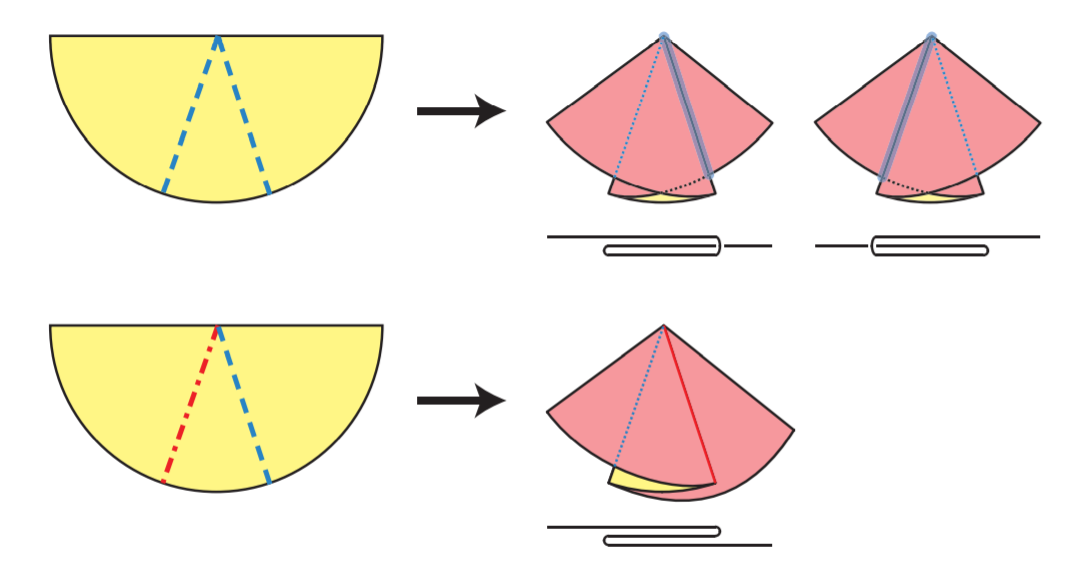
考虑角$\theta{i}$和与之相邻的两个角$\theta{i-1}$和$\theta_{i+1}$,如果有
$\theta{i-1}>\theta{i}<\theta_{i+1}$
则称$\theta_{i}$为局部最小角,这个局部最小角对应的两条折痕必然是一山一谷(下图)
$proof:$
如果两条边都是山折(谷折),那么将会穿破纸层(上图)