折叠三次曲线
取一张纸,选取一个定点$p_1$并在纸的下边上任选一点$p_1^ { \prime }$
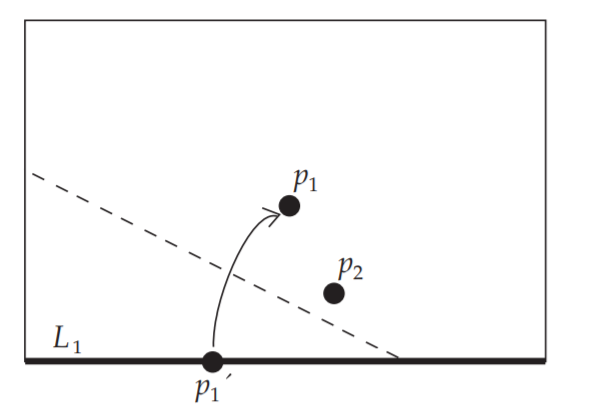
折叠,使$p_1$和$p_1^ { \prime }$重合,标注$p_2$所对应的位置
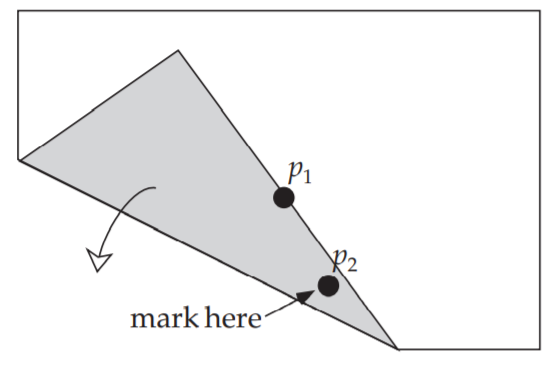
展开,便得到了$p_2$关于折线的对称点$p_2^ { \prime }$
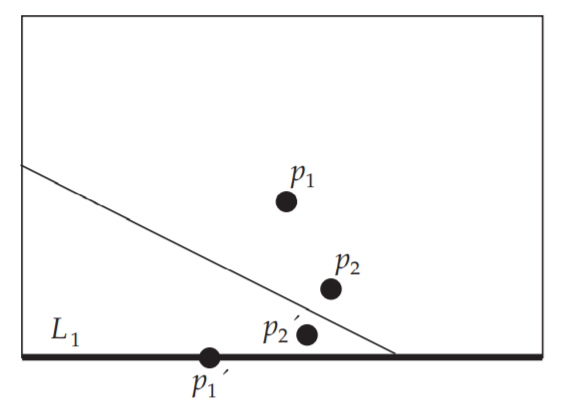
我们可以借助$GeoGebra$去研究$p_2’$的轨迹
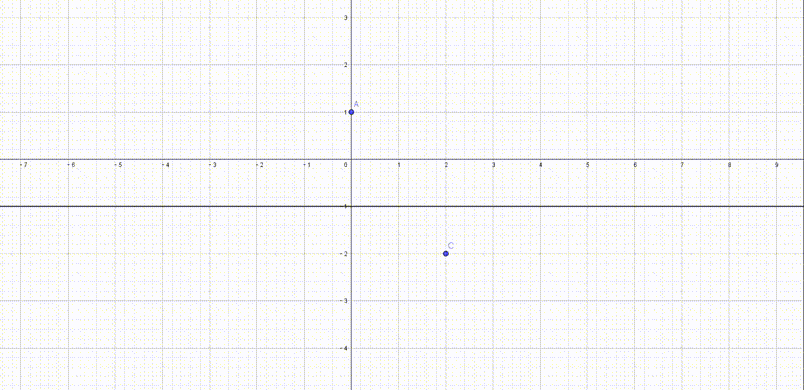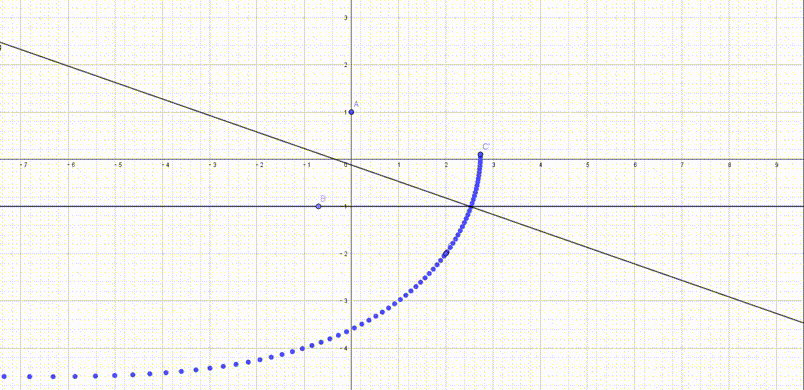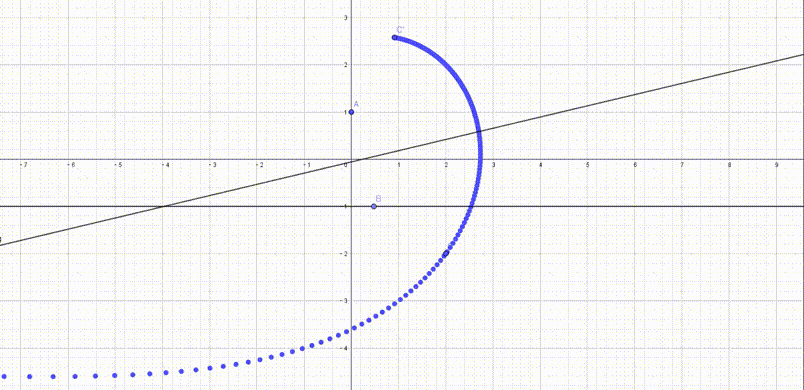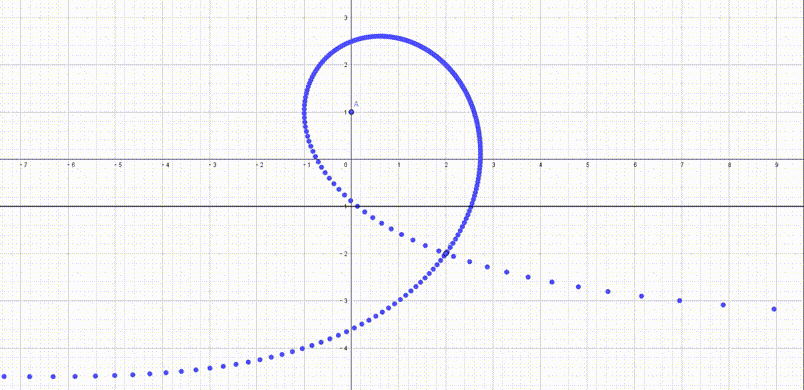
看起来很有意思,那么这个轨迹的方程是什么呢?
分析
像抛物线折叠建立坐标系
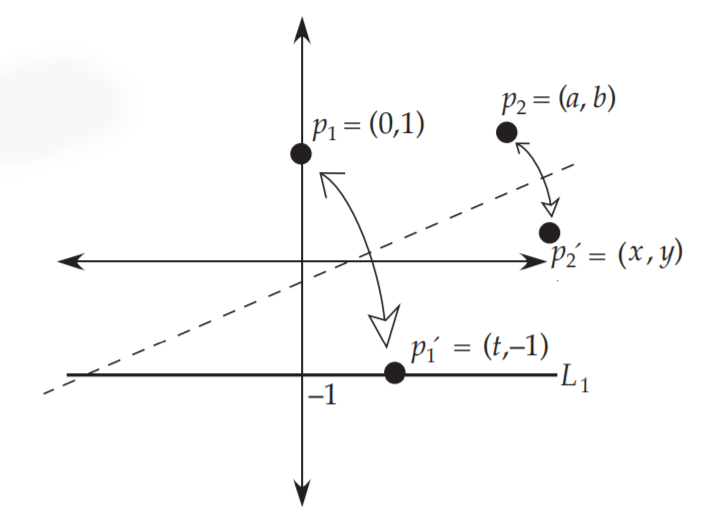
折线的方程和抛物线折叠一模一样,为
${ y = \frac { t } { 2 } x - \frac { t ^ { 2 } } { 4 } }$
又$ p p { 1 } ^ { \prime }$和$p { 2 } p _ { 2 } ^ { \prime }$都垂直于折线,所以
$ { k { p p { 1 } ^ { \prime } } = k { p { 2 } p _ { 2 } ^ { \prime } } } $
$ { \frac { - 1 - 1 } { t } = \frac { y - b } { x - a } \Rightarrow - \frac { 2 } { t } = \frac { y - b } { x - a } } $
解出$t$
$ { t = - \frac { 2 ( x - a ) } { y - b } = \frac { 2 ( a - x ) } { y - b } } $
设$p2^{\prime}$坐标为$(x,y)$,则$p { 2 } p _ { 2 } ^ { \prime }$中点坐标为
$ { ( \frac { x + a } { 2 } , \frac { y + b } { 2 } ) } $
因为这两点关于折线对称,故中点在折线上,带入得
$ { \frac { a - x } { y - b } \cdot ( \frac { x + a } { 2 } ) - ( \frac { a - x } { y - b } ) ^ { 2 } = \frac { y + b } { 2 } } $
化简得
$ { ( a ^ { 2 } - x ^ { 2 } ) \cdot ( y - b ) - 2 ( a - x ) ^ { 2 } = ( y + b ) ( y - b ) ^ { 2 } } $
$ y ^ { 3 } + x ^ { 2 } y - b y ^ { 2 } + ( 2 - b ) x ^ { 2 } - b y ^ { 2 } - 4 a x - ( a ^ { 2 } + b ^ { 2 } ) y + a ^ { 2 } b + 2 a ^ { 2 } + b ^ { 3 } = 0$
这显然是一个三次曲线的方程
斜率与三次方程的解
对任意三次方程$x^{3}+a x^{2}+b x+c=0$,我们可以令$z=x-\frac{1}{3} a$,于是方程便转换为
$z^{3}+\frac{3 b-a^{2}}{3} z-\frac{9 a b-27 c-2 a^{3}}{27}=0$
从而从$x^{3}+a x^{2}+b x+c=0$转化到了$x^{3}+ ax+b=0$
考虑两条抛物线
$l_1:\,\left(y-\frac{1}{2} a\right)^{2}=2 bx \quad and \quad l_2:\,y=\frac{1}{2} x^{2}$
设$\ell$为这两个抛物线的共同切线,斜率为$m$,且与$l1$相切与$\left(x{1}, y{1}\right)$,与$l_2$相切与$\left(x{2}, y_{2}\right)$
对$l_1$两边同时求导
$ { y ^ { 2 } - a y + \frac { 1 } { 4 } a ^ { 2 } = 2 b x } $
$ { 2 y \cdot \frac{\mathrm{d} y}{\mathrm{d} x} - a \frac{\mathrm{d} y}{\mathrm{d} x} + 0 = 2 b } $
整理得
$ { \frac{\mathrm{d} y}{\mathrm{d} x} = \frac { 2 b } { 2 y - a } = \frac { b } { y - \frac { 1 } { 2 } a } } $
带入$y_1$
$y_{1}-\frac{1}{2} a=\frac{b}{m}$
所以我们可以用$m$表示$x_1$和$y_1$
$x{1}=\frac{\left(y{1}-\frac{1}{2} a\right)^{2}}{2 b}=\frac{\left(\frac{b}{m}\right)^{2}}{2 b}=\frac{b}{2 m^{2}}$
$y_{1}=\frac{b}{m}+\frac{a}{2}$
同理,对$l_2$求导得
$x_{2}=m$
$y_{2}=\frac{m^{2}}{2}$
我们知道,过$\left(x{1}, y{1}\right)$和$\left(x{2}, y{2}\right)$的直线斜率为
$m=\frac{y{2}-y{1}}{x{2}-x{1}}$
带入得
$m=\frac{y{2}-y{1}}{x{2}-x{1}}=\frac{\frac{m^{2}}{2}-\left(\frac{b}{m}+\frac{a}{2}\right)}{m-\frac{b}{2 m^{2}}}=\frac{m^{4}-2 b m-a m^{2}}{2 m^{3}-b}$
即
$m^{3}+a m+b=0$
说明$m$为方程$x^{3}+ ax+b=0$的解
尝试求解$x^3-7x-6=0$,先构造两个抛物线
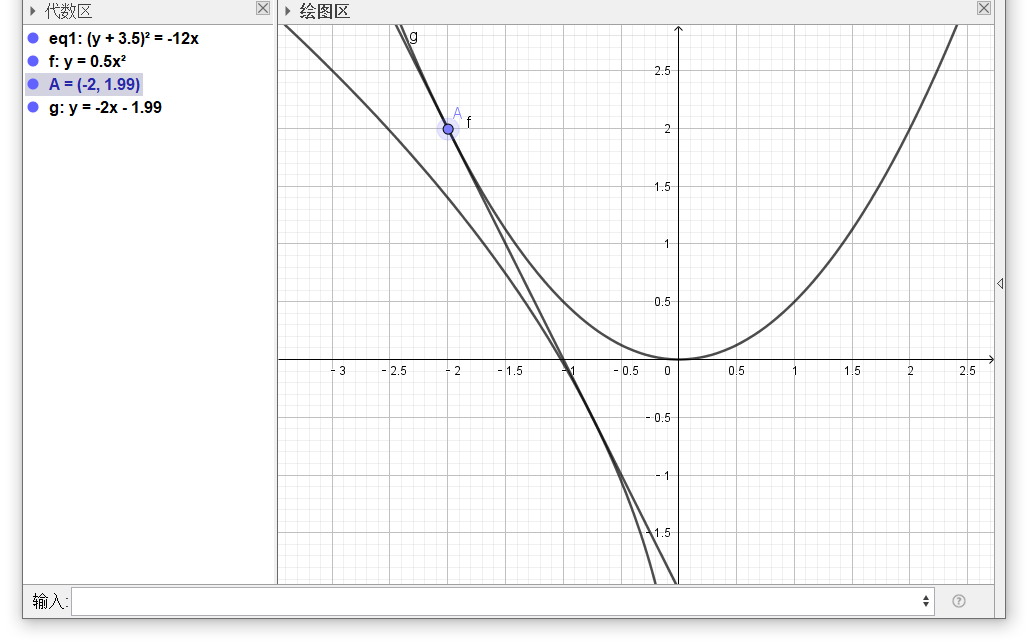
注意$g$的斜率
$x=-2$
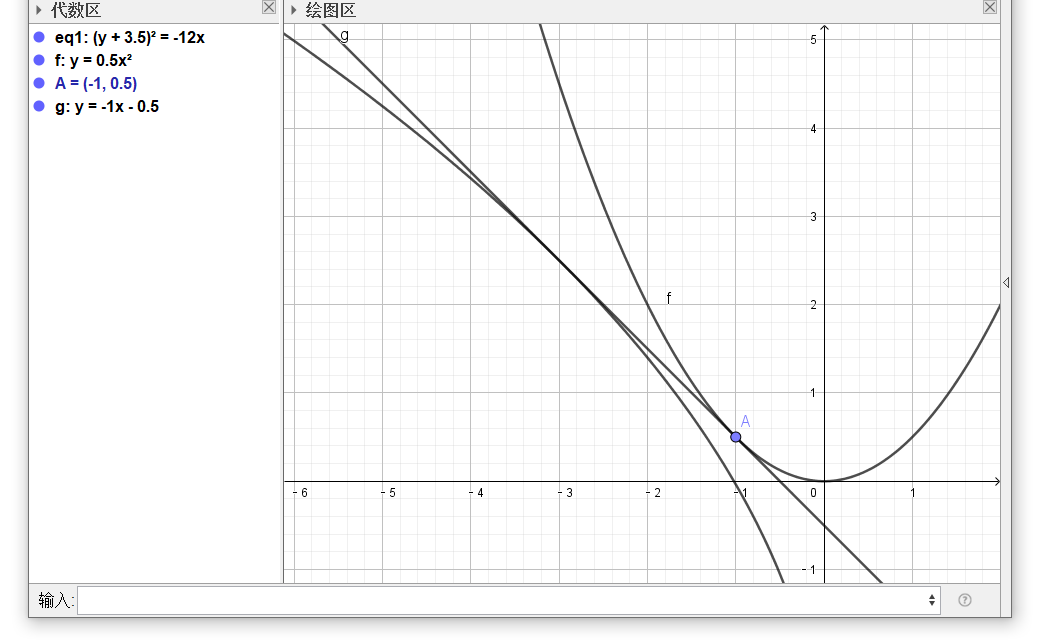
$x=-1$
$x=3$
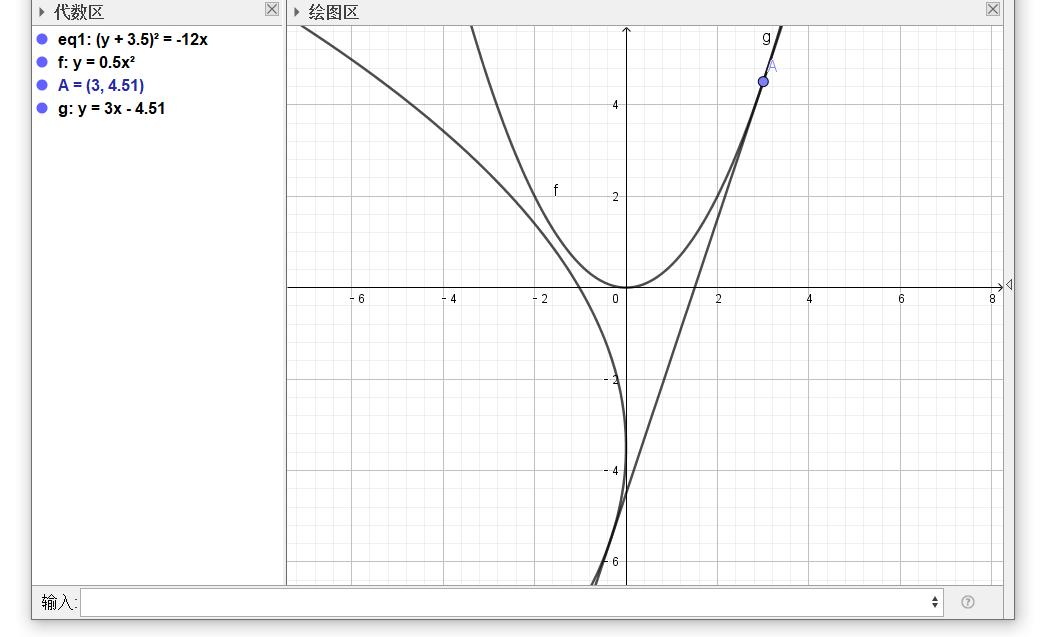
于是我们便获得了这个三次方程的三个解$x=-2,-1,3$
那么,怎么用折纸的方法构造呢?
容易看出,$l_1$的焦点为$(\frac b 2,\frac a 2)$,准线为$x=-\frac b 2$,$l_2$的焦点为$(0,\frac{1}{2})$,准线为$y=-\frac{1}{2}$
根据上一节的抛物线折叠的性质,我们同时分别将点$(\frac b 2,\frac a 2)$折到$x=-\frac b 2$上,将点$(0,\frac{1}{2})$折到$y=-\frac{1}{2}$上,所形成的折现即为两条抛物线的共同切线,至于为什么可以做到,我们将在下一节讨论折纸公理六时详细阐述。
三次函数
拐点