随机变量

随机变量$X$是有限或无限可数样本空间$S$到实数的函数

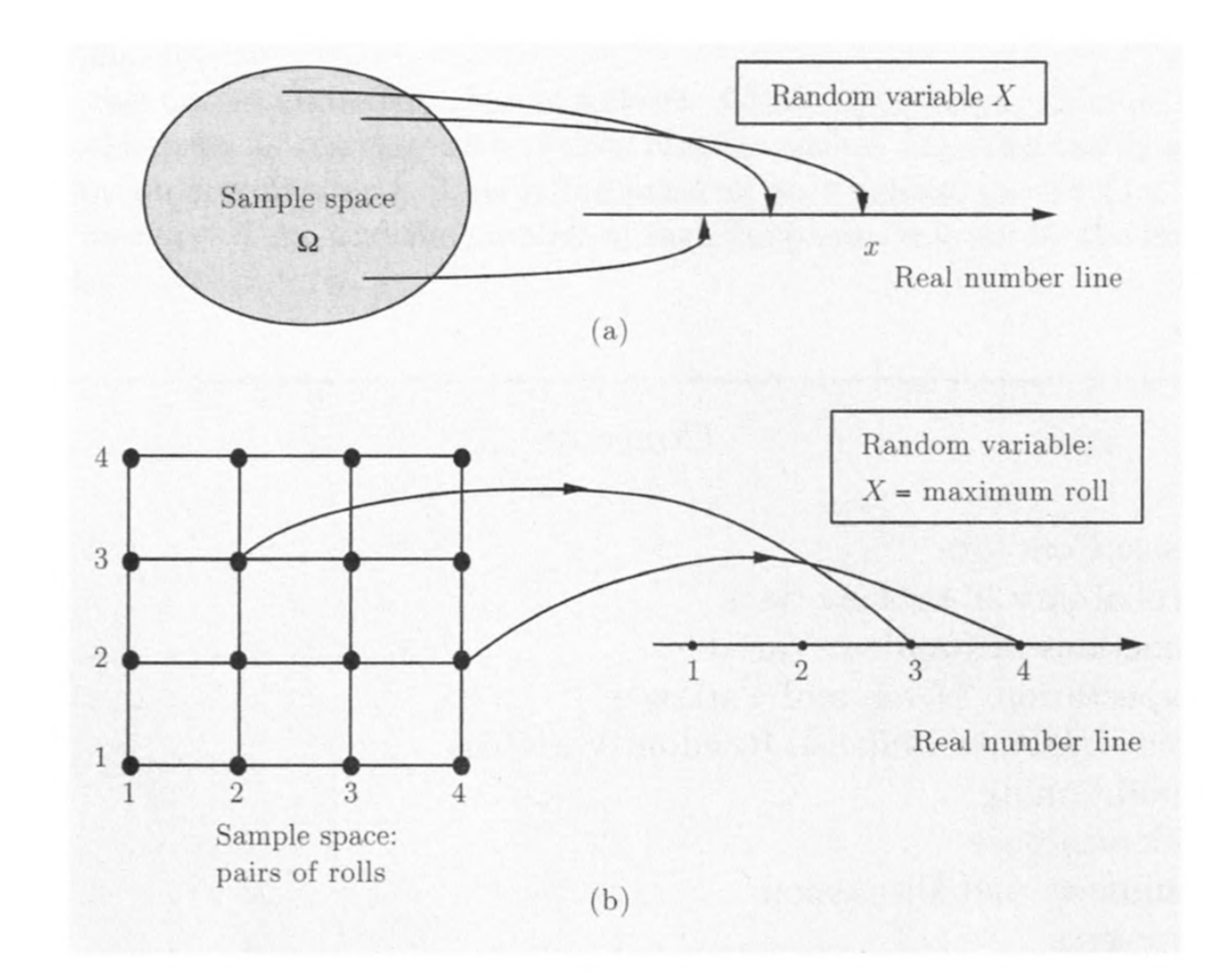
对于随机变量$X$和实数$x$，定义事件$X=x$为${s\in S,X(s)=x}$，因此

we will use upper case characters to denote random variables， and lower case characters to denote real numbers such as the numerical values of a random variable.

$\Pr\{X=x\}=\sum_{s\in S,X(s)=x}\Pr\{s\}$

对于随机变量，函数$p_X(x)=\Pr{X=x}$为$X$的概率质量函数PMF

PDF

特别的，对于连续随机变量也称为概率密度函数PDF

$\Pr\{X\in B\}=\int_Bf_X(x)\text{d}x$

归一化条件为

$\int_{-\infty}^{+\infty}f_X(x)\text{d}x=1$ $\Pr\{[x,x+\delta ]\}\approx f_X(x) \delta$

所以$f_X(x)$可以看成单位长度的概率

可以把这两种函数整合成一个函数

即为累积分布函数CDF(cumulative distribution function)

$F_x(x)=\text{Pr}\{X\le x\}=\begin{cases}\displaystyle\sum_{k\le x}p_X(k) \\\displaystyle\int_{-\infty}^xf_X(x)\text{d}x\end{cases}$

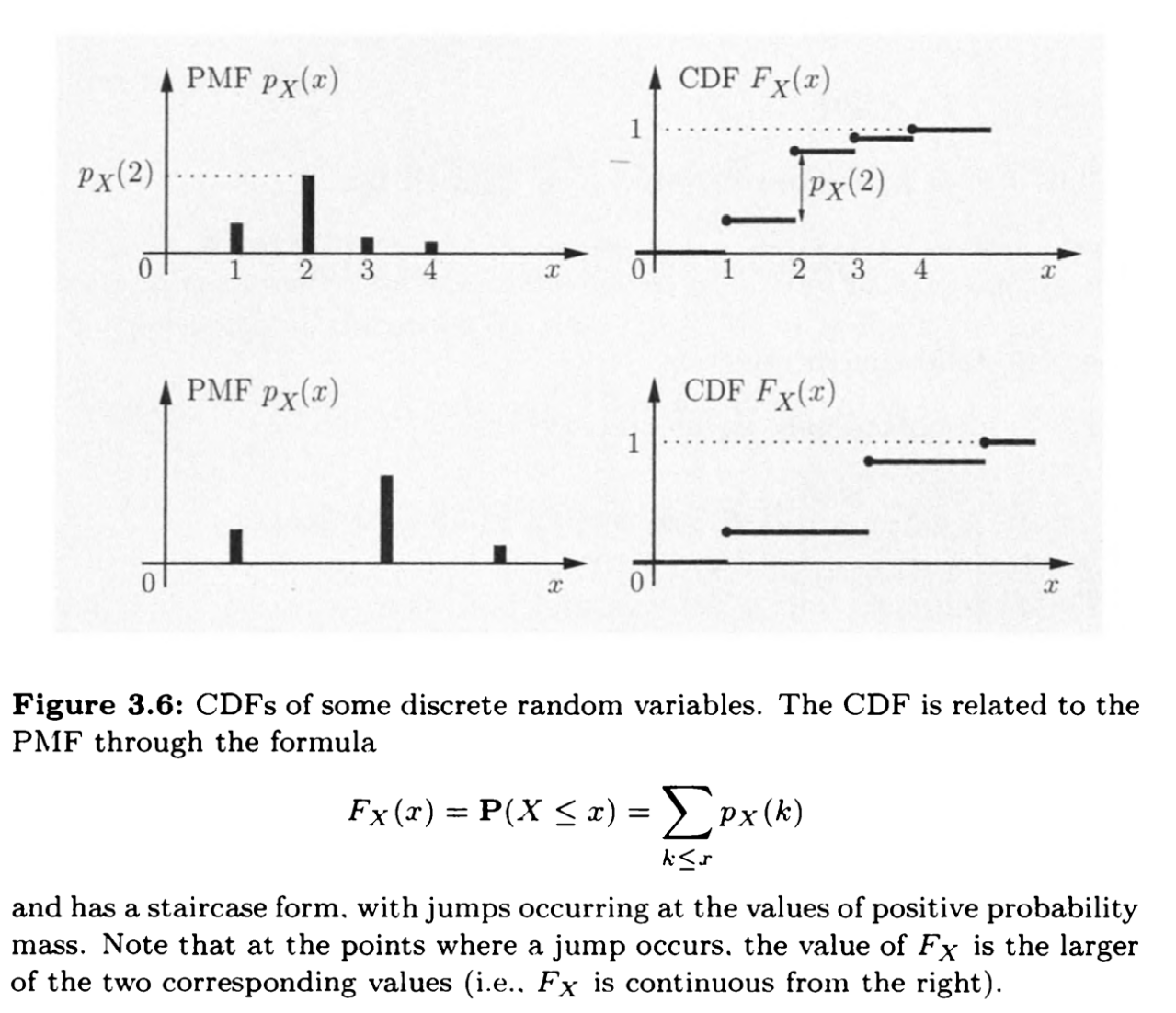
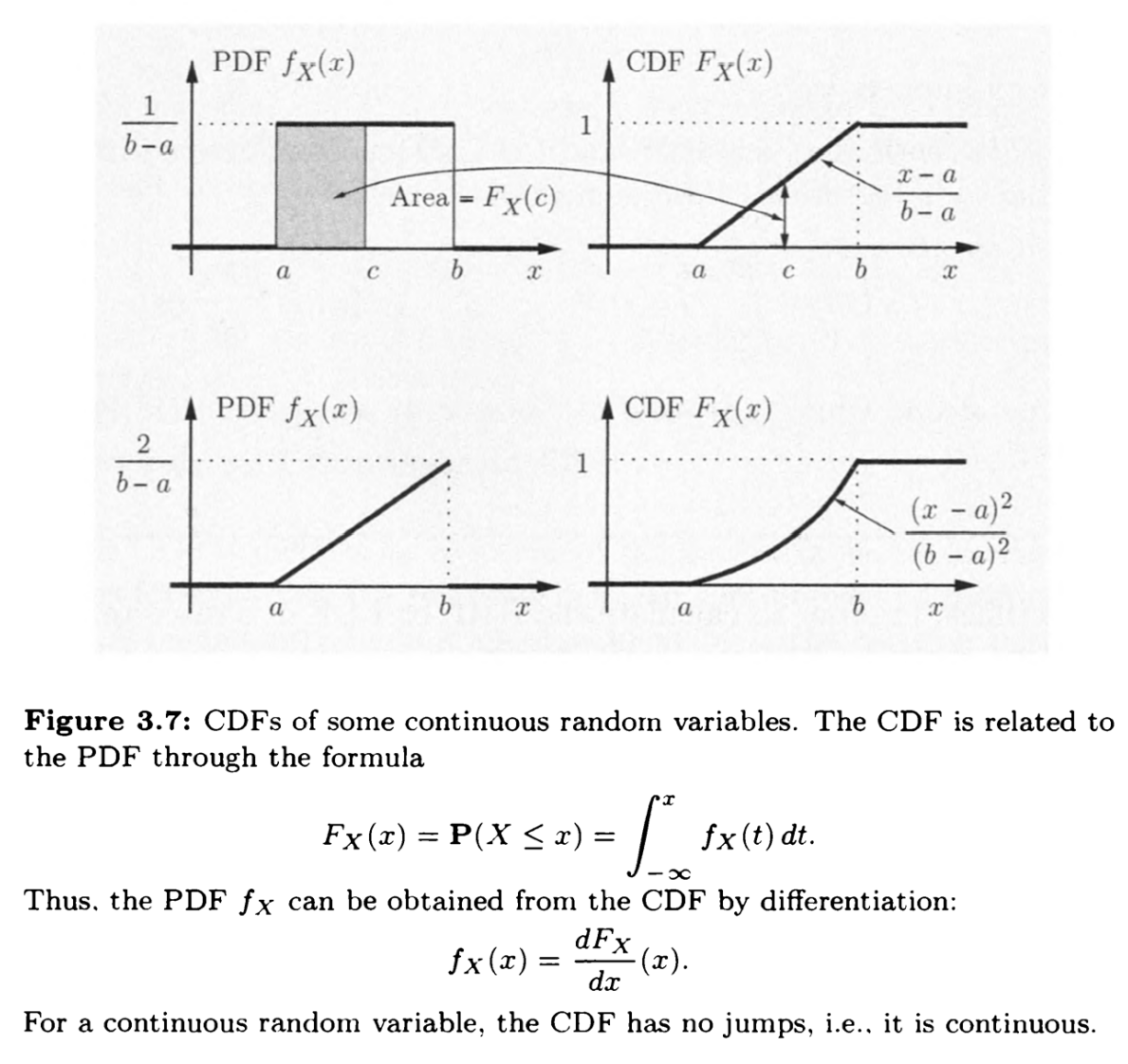
可以类比积分上限函数，通过差分和求导可以还原

若有若干个随机变量，即为多维随机变量

则有联合PMF

$p_{X,Y}(x,y)=\Pr\{X=x且Y=y\}\\ p_{X}(x)=\Pr\{X[1]=x[1],\cdots,X[d]=x[d]\}\\ \sum_{x[1]\in X_1}\sum_{x[2]\in X_2} \cdots\sum_{x[d]\in X_d}=1$

为$X$与$Y$的联合概率密度函数，性质同理，

如边缘$\rm PMF$

$\begin{aligned}\Pr\{Y=y\}&=\sum_x\Pr\{X=x且Y=y\}(y为定值)\\&=\sum _xp_{X,Y}(x,y)\end{aligned}\\$ $p_Z(z)=\sum_{\{z|z=g(x,y)\}}p_{X,Y}(x,y)\\ \text{E}[g(X, Y)]=\sum_{x} \sum_{y} g(x, y) p_{X, Y}(x, y)$

函数

$Y=g(X)\\p_Y(y)=\sum_{\{x|g(x)=y\}}p_X(x)$

边缘函数

设$(X,Y)$的联合分布为$F(X,Y)$则

$F_X(x)=P(X\le x)$

为随机变量$X$的边缘分布函数

$f_X(x)=\int_{-\infty}^{+\infty}f(x,y)\text dy$

为边缘密度函数

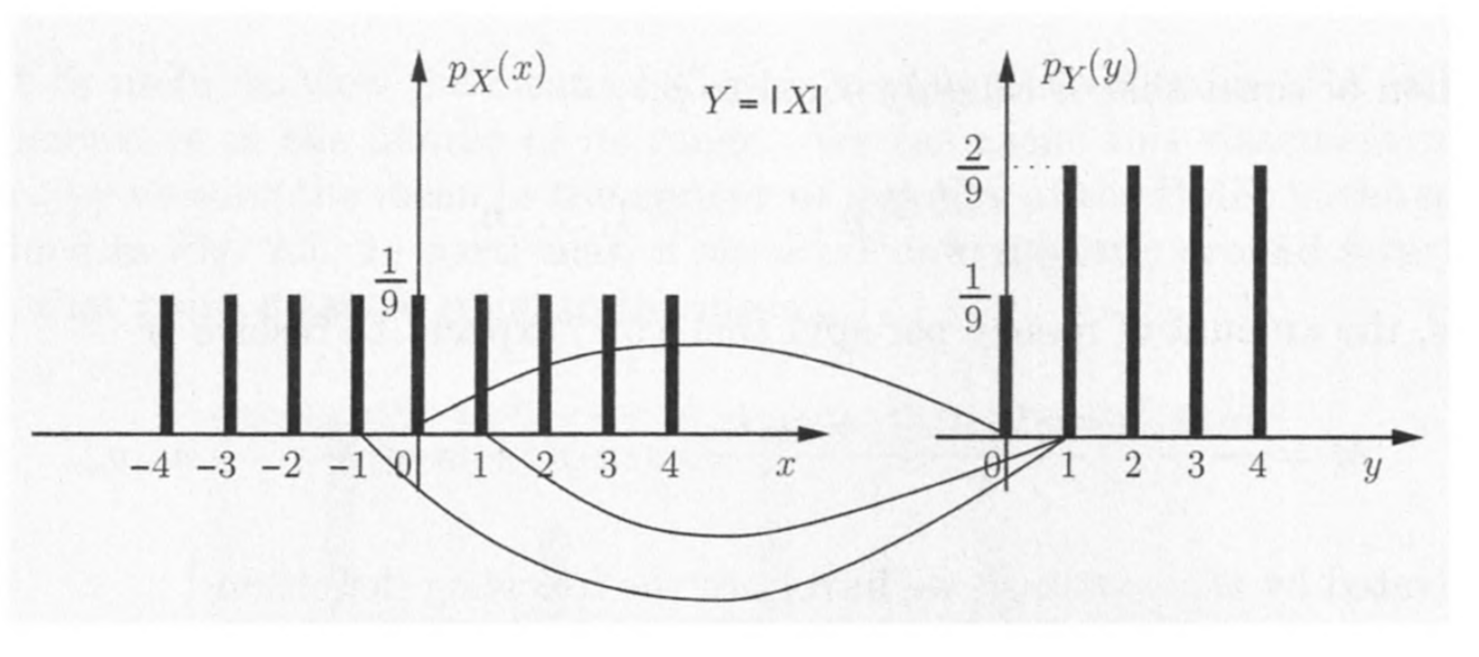
利用定义可以求$Z=g(X,Y)$的分布

$F_Z(z)=\iint_{g(x,y)\le z}f(x,y)\text dx\text dy$

从而有

$f_Z(z)=\frac{\text d F_Z(z)}{\text d z}$

随机变量的期望值

$\text E[X]=\sum_xx\cdot\Pr\{X=x\}\\ \text E[g(X)]=\sum_xg(x)\cdot\Pr\{X=x\}\\$

对于连续的随机变量

$\text{E}[X]=\int_{-\infty}^{+\infty}xf_X(x)\text{d}x\\ \text{E}[g(X)]=\int_{-\infty}^{+\infty}g(x)f_X(x)\text{d}x$

期望的线性性质

$\text E\left[\sum_{i=1}^nX_i\right]=\sum_{i=1}^n\text E[X_i]\\\text E[aX+b]=a\text E[X]+b$

若相互独立，使用期望的定义得

$\text E[XY]=\text E[X]\text E[Y]$

方差

$\text{Var}[X]=\text{E}[(X-\text{E}[X])^2]=\text{E}[X^2]-\text{E}^2[X]\\ \text{Var}[aX+b]=a^2\text{Var}[X]$

对于连续的随机变量

$\text{Var}[X]=\int_{-\infty}^{+\infty}(x-\text{E}[X])^2f_X(x)\text{d}x\\$ $\text{Var}[X\pm Y]=\text{Var}[X]+\text{Var}[Y]\pm2E[(X-E[X])(Y-E[Y])]$

若相互独立

$\text{Var}[X\pm Y]=\text{Var}[X]+\text{Var}[Y]\\ \text{Var}[\sum_{i=1}^nX_i]=\sum_{i=1}^n\text{Var}[X_i]$ $\begin{aligned}\text{Var}[XY]&=\text{E}^2[Y]\text{Var}[X]+\text{E}[X^2]\text{Var}[Y]\\ &=\text{E}[Y]^2\text{Var}[X]+\text{E}^2[X]\text{Var}[Y]\\ &=\text{Var}[X]\text{Var}[Y]+\text{E}^2[Y]\text{Var}[X]+\text{E}^2[X]\text{Var}[Y] \end{aligned}$

标准差

$\sigma_X=\sqrt{\text{var}(X) }$

矩

随机变量使用概率密度函数描述，概率密度函数具有一个特性，称为 矩 Moment，矩是随机变量幂的期望。我们重点关注两种矩：

$k$阶原点矩，$\text E\left[ X^{k} \right]$
$k$阶中心距，$\text E\left[ (X-\text E[x]) \right]^{k}$

随机矩阵

对于矩阵$\tilde{X}(d_1,d_2)$，其均值为

$\mathrm{E}(\tilde{X}):=\begin{bmatrix}\mathrm{E}\left(\tilde{X}[1,1]\right)&\mathrm{E}\left(\tilde{X}[1,2]\right)&\cdots&\mathrm{E}\left(\tilde{X}[1,d_2]\right)\\\mathrm{E}\left(\tilde{X}[2,1]\right)&\mathrm{E}\left(\tilde{X}[2,2]\right)&\cdots&\mathrm{E}\left(\tilde{X}[2,d_2]\right)\\&&\cdots\\\mathrm{E}\left(\tilde{X}[d_1,1]\right)&\mathrm{E}\left(\tilde{X}[d_1,2]\right)&\cdots&\mathrm{E}\left(\tilde{X}[d_1,d_2]\right)\end{bmatrix}$

线性性质

$\mathrm{E}(A\tilde x+B)=A\mathrm{E}(\tilde x) +B$

独立

若对于一切$x,y$

$F(x,y)=F_X(x)F_Y(y)$

则称两随机变量相互独立

卷积

$Z=X+Y$

则有

$f_Z(z)=\int_{-\infty}^\infty f_X(x)f_{Y}(z-x)\text dx$

协方差

$\mathbf{Cov}(X,Y)=E\{[X-E(X)][Y-E[Y]]\}$

类比有

$\mathbf{Cov}(X,Y)=E(XY)-E(X)E(Y)$

条件

conditional PMF

$p_{X|A}=\frac{\text{Pr}\{\{X=x\}\cap A \}}{\text{Pr}\{A\}}$

可以将A推广为一个随机变量

$p_{X|Y}(x,y)=\frac{p_{X,Y}(x,y)}{p_Y(y)}$

$\sum_{x} p_{X \mid Y}(x \mid y)=1$

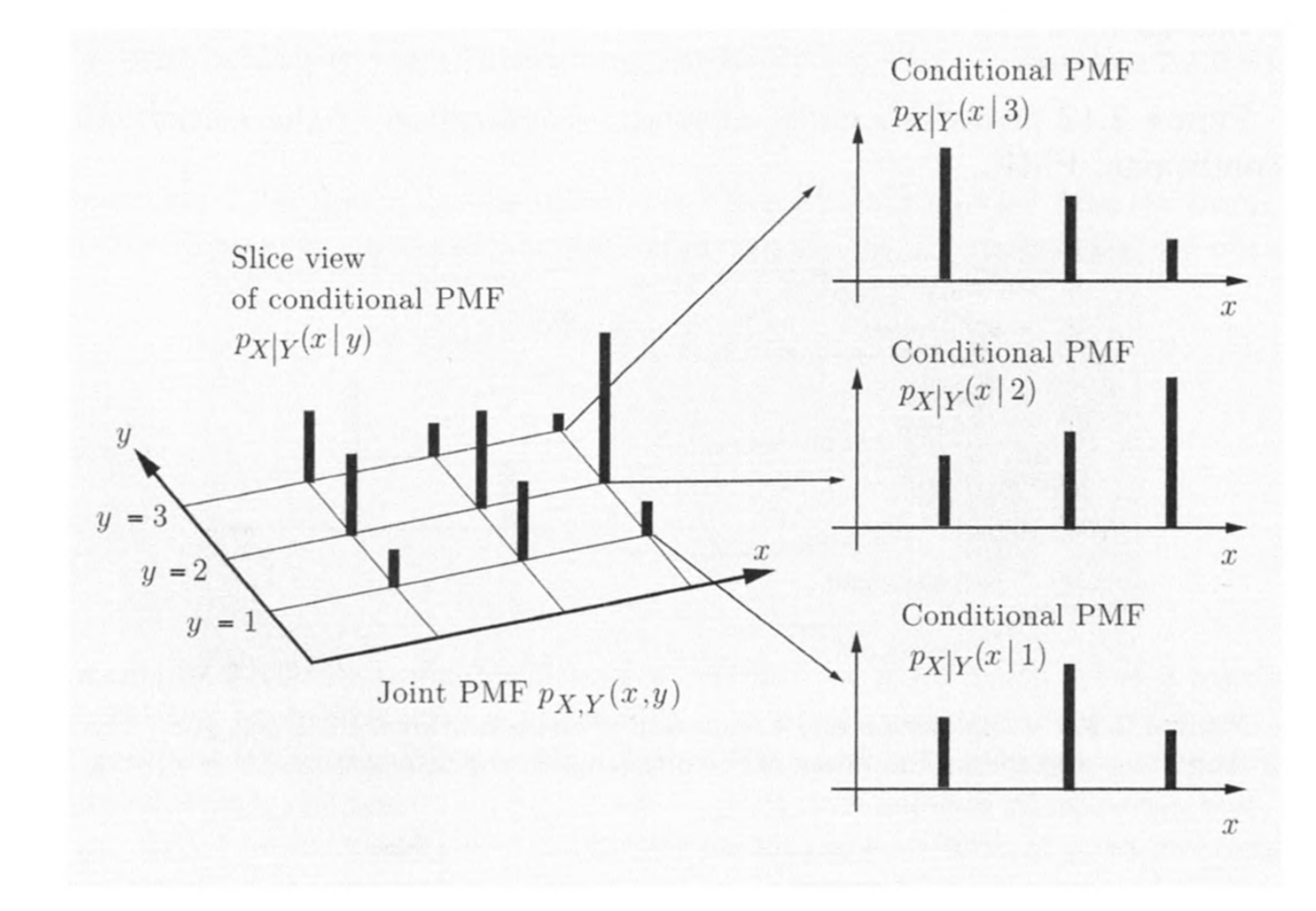
分布

离散

几何分布

前面一直没有成功直到第n次才成功

$\Pr\{X=k\}=(1-p)^{n-1}p\\ \text E[x]=\sum_{k=1}^\infty(1-p)^{k-1}pk=1/p$

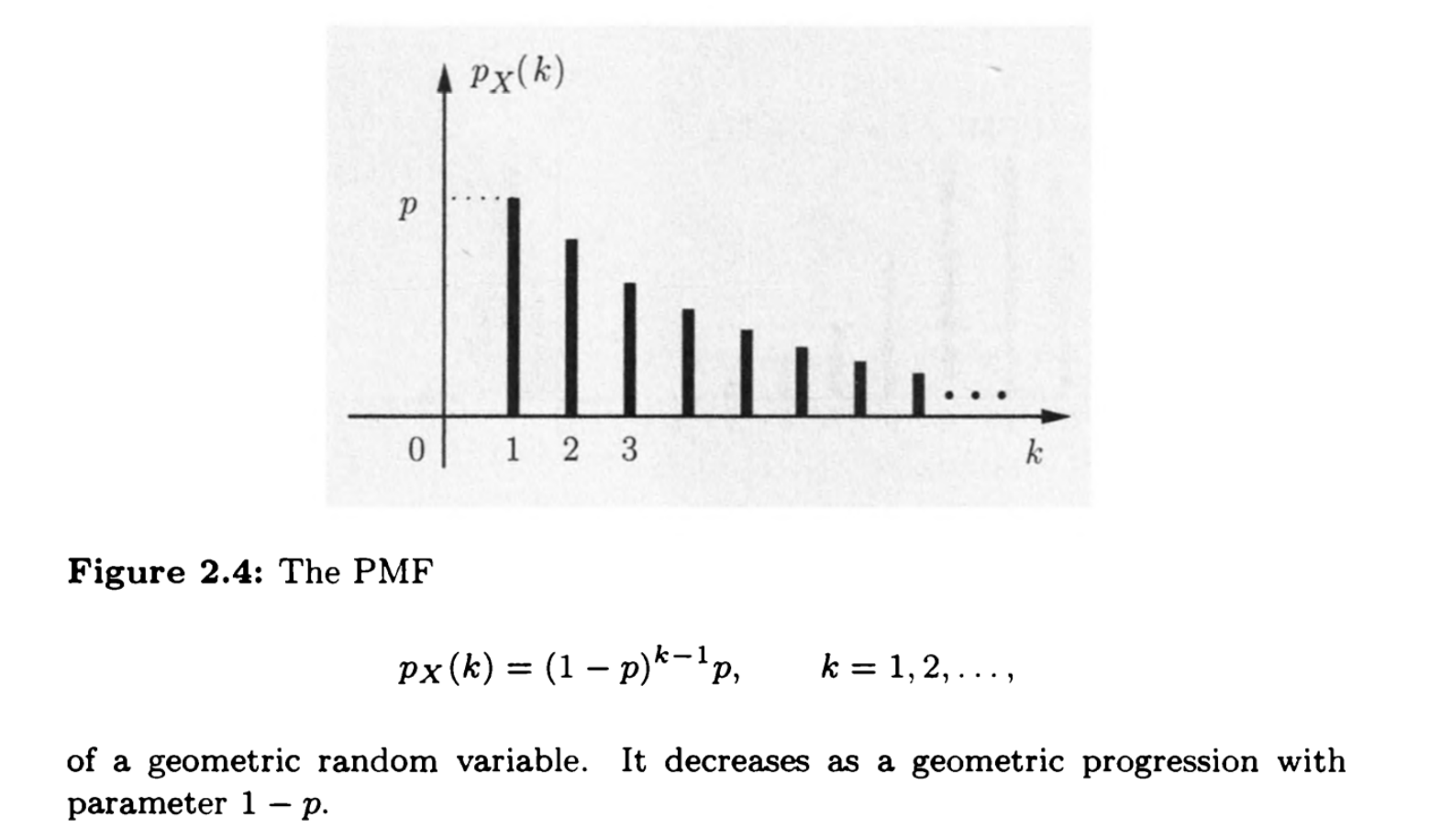
二项分布

区别于国内表达，组合数记为

$\left(\begin{array}{l}n\\k\end{array}\right)=C_n^k$

读作$n$取$k$

$\Pr\{X=k\}=\left(\begin{array}{l}n\\k\end{array}\right)p^k(1-p)^{n-k}\\ \text E[X]=np\\ \text{Var}[X]=np(1-p)$

泊松分布

在某段时间内事件发生的概率为

$p=\lambda t$

则$t=0\to1$发生的次数可以表示为

$p_X(k)=e^{-\lambda}\frac{\lambda^k}{k!}\\ \sum_{k=0}^{\infty} e^{-\lambda} \frac{\lambda^{k}}{k !}=e^{-\lambda}\left(1+\lambda+\frac{\lambda^{2}}{2 !}+\frac{\lambda^{3}}{3 !}+\cdots\right)=e^{-\lambda} e^{\lambda}=1\\$

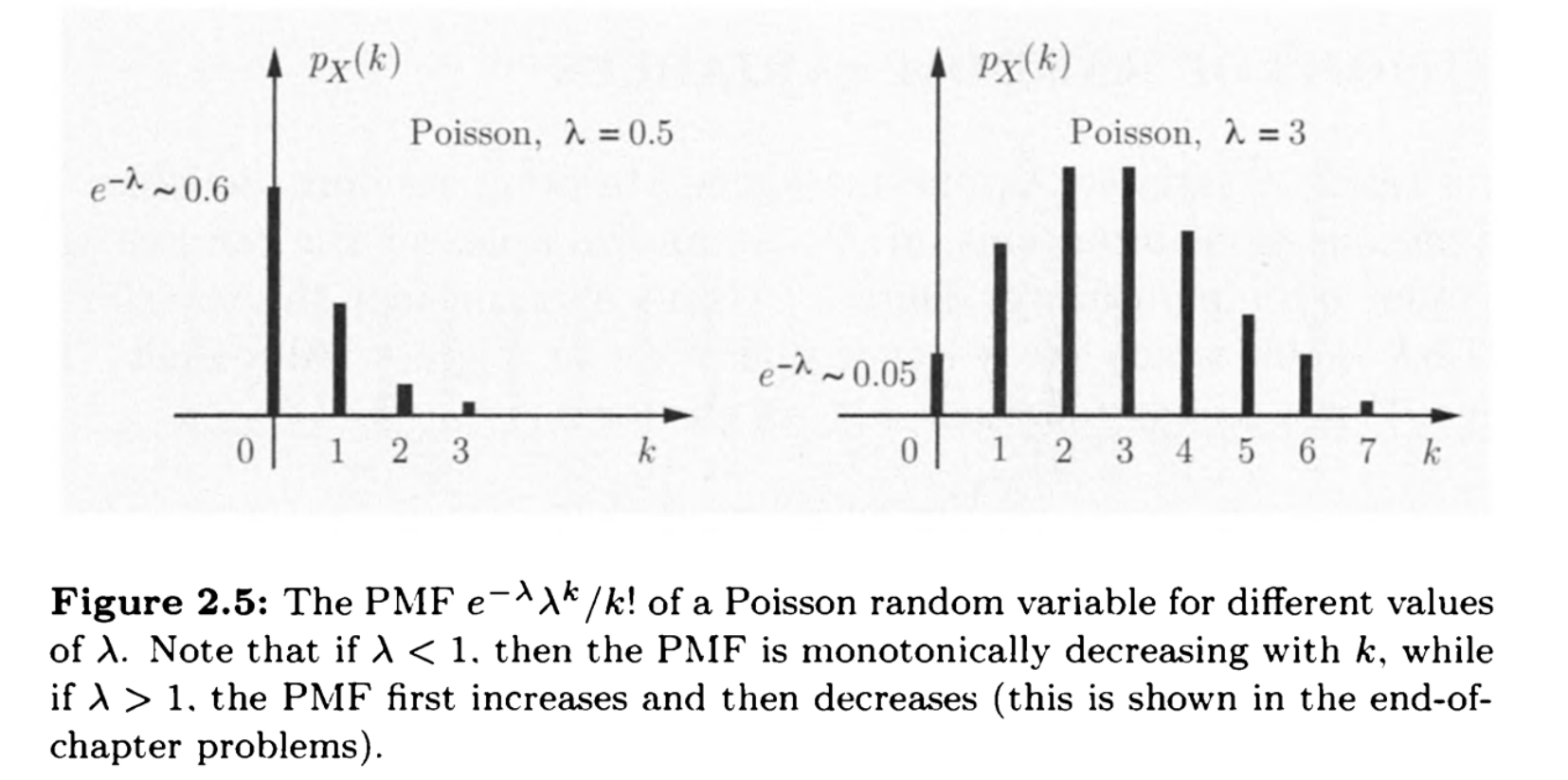
连续

均匀分布

$f_X(x)=\begin{cases}\frac{1}{b-a},&a\leq x\leq b,\\0,&\text{otherwise,}\end{cases}$

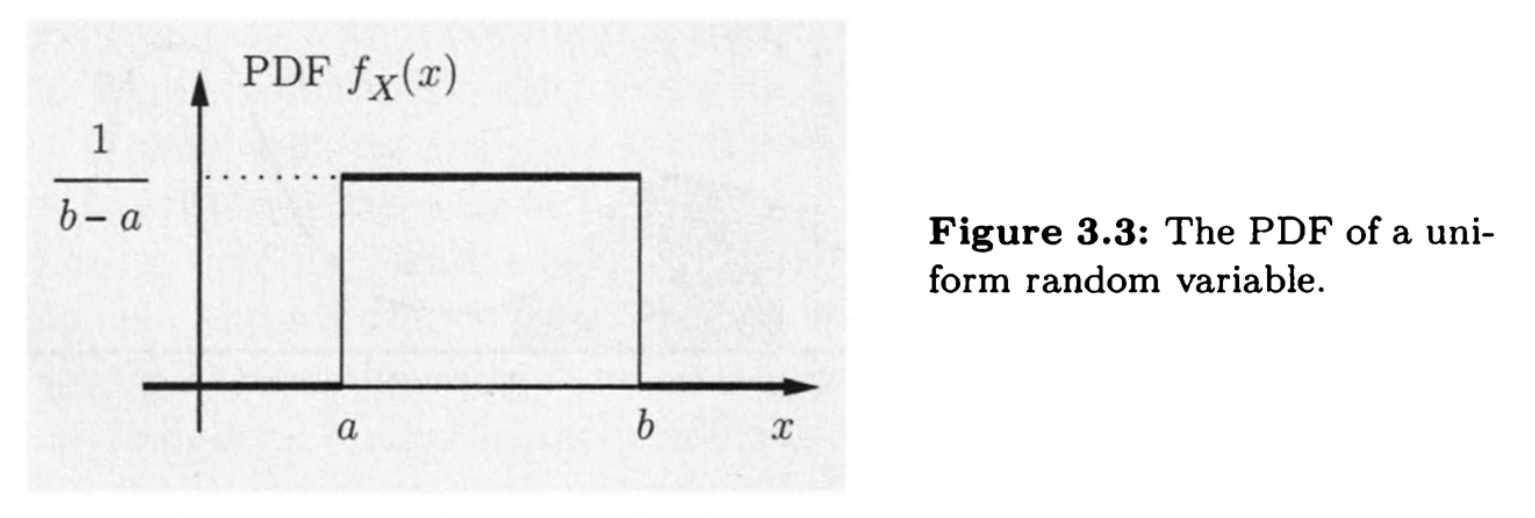
记为$X\sim U(a,b)$

则可以写出分布的期望和方差

$\mathbf{E}[X]=\frac{a+b}{2}\\ \mathbf{Var}[X]=\frac{(b-a)^2}{12}$

指数分布

$f_{X}(x)=\left\{\begin{array}{ll} \lambda e^{-\lambda x}, & \text { if } x \geq 0 \\ 0, & \text { otherwise } \end{array}\right.$

记为$X\sim E(\lambda)$

其中$\lambda$是参数可以用来调控均值，这个模型用途很广

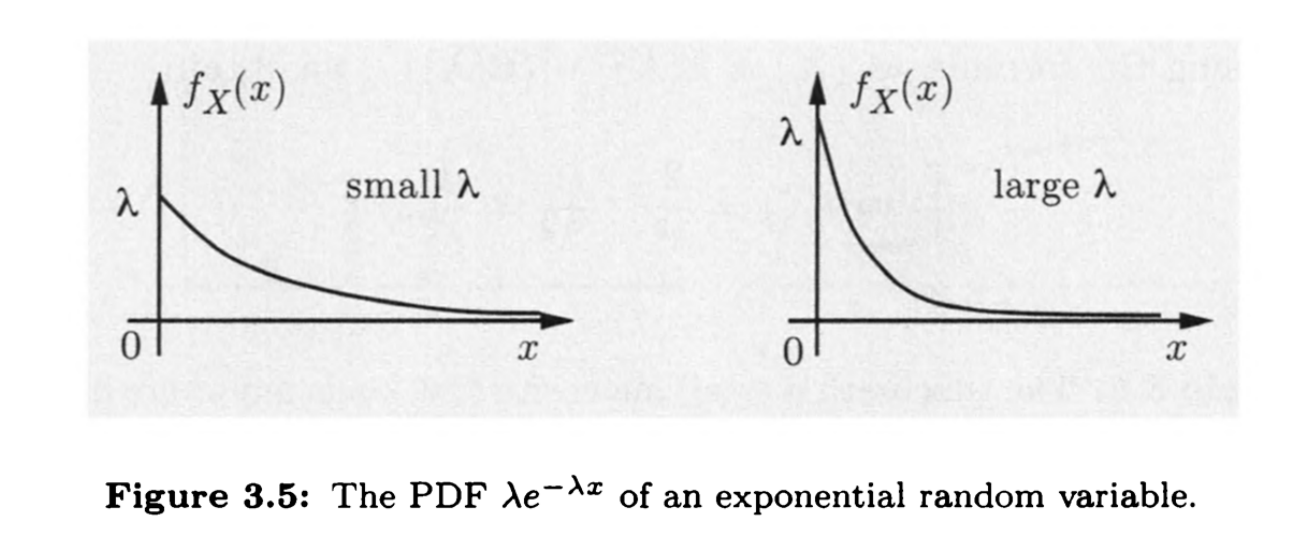
类似与几何分布的情况，只不过用到了泊松分布的假设

$\mathbf{E}(X)=\frac1\lambda,\text{var}=\frac1{\lambda^2}$

正态分布

自然界许多现象都遵循 正态分布 Normal Distribution。正态分布又称为 高斯分布 Gaussian Distribution （纪念著名数学家卡尔·弗莱德利希·高斯），其表达式如下：

$f \left( x; \mu , \sigma ^{2} \right) = \frac{1}{\sqrt[]{2 \pi \sigma ^{2}}}e^{\frac{- \left( x- \mu \right) ^{2}}{2 \sigma ^{2}}}$

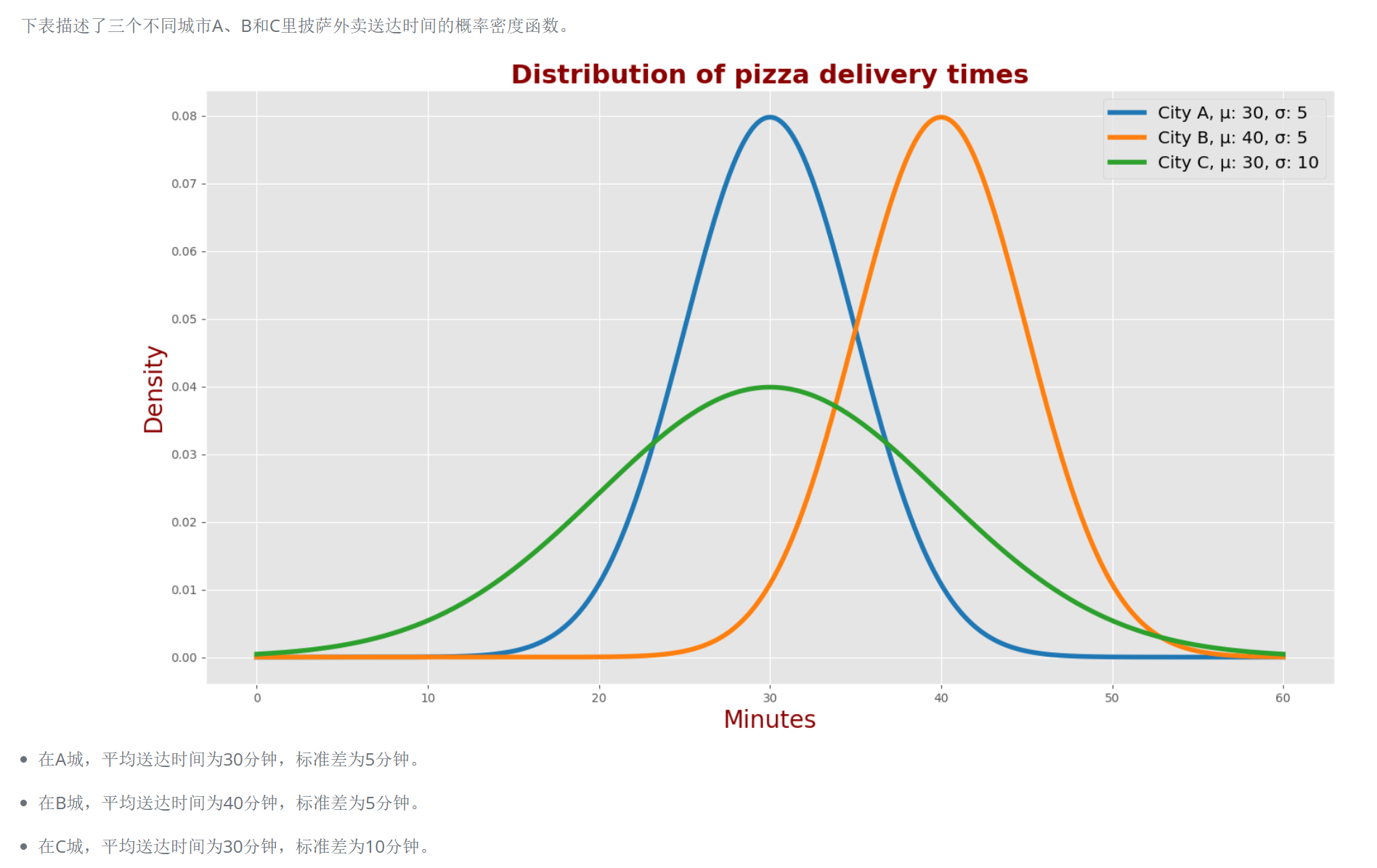
记为$X\sim N(\mu,\sigma^2)$，若$\mu=\sigma=1$则为标准正态分布

$f_X(x)=\frac1{\sqrt{2\pi}\sigma}e^{-(x-\mu)^2/2\sigma^2}$ $\text{E}[X]=\mu, \quad \operatorname{Var}(X)=\sigma^{2}$

可以利用标准正态分布函数来计算概率

$P(a<X<b)=\Phi\left(\frac{b-\mu}\sigma\right)-\Phi\left(\frac{a-\mu}\sigma\right)$

可加性

$kX+lY\sim N(k\mu_1+l\mu_2,k^2\sigma_1^2+l^2\sigma_2^2)$

分位数

$\Phi(u_p)=P(X\le u_p)=p$

则称$u_p$为标准正态分布的$p$分位数

$\Phi(-u_p)=1-p$

最值

$X_i$服从同一分布，则

$U=\max\{X_i\},V=\min\{X_i\}\\ f_U(x)=n[f(x)]^{n-1}f(x)\\ f_V(x)=n[1-f(x)]^{n-1}f(x)$

数字特征

偏度

$\beta_s(X)=\frac{E\{[X-\mathbf E(X)]^3\}}{[\mathbf{Var}[X]]^{3/2}}$

$\beta_s(X)<0$为左偏，左侧有较长的尾部，反之同理

峰度

$\beta_k(X)=\frac{E\{[X-\mathbf E(X)]^4\}}{[\mathbf{Var}[X]]^{2}}-3$

峰度和正态分布比较

变异系数

$C_v(X)=\frac{\sigma(X)}{|E(X)|}$

用均值标准化

中心极限定理

切比雪夫不等式，若$E(X^2)<+\infty$

$P(|X-E(X)|\ge \varepsilon)\le\frac{\mathbf{Var}(X)}{\varepsilon^2}$

马尔可夫不等式，若$E(|X|^p)<+\infty$

$P(|X|\ge \varepsilon)\le\frac{E(|X|^p)}{\varepsilon^p}$

样本均值

$\overline{X}=\frac1n\sum_{i=1}^nX_i\sim N\left(\mu,\frac{\sigma^2}n\right)\\ \overline{Y_n}=\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\sim N(0,1)$

或者

$\sum_{i=1}^nX_i\sim N\left(n\mu,n\sigma^2\right)$

$\chi ^2$分布

若$X_i$服从标准正态，则$U$服从自由度为$n$的$\chi ^2$分布

$U=\sum_{i=1}^nX_i^2\sim\chi^2(n)\\ \mathbf E(U)=n,\mathbf{Var}(U)=2n$

样本方差

$S^2=\frac1{n-1}\sum_{i=1}^n(X_i-\overline X)^2\\\frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1)$

$\overline X$和$S^2$相互独立

可加性

$U_1\sim \chi^2(m),U_2\sim \chi^2(n)\\ U_1+U_2\sim \chi^2(m+n)$

$t$分布

若$X\sim N(0,1),Y\sim \chi^2(n)$

$T= \frac{X}{\sqrt{Y/n}}\sim t(n)$

F分布

$U\sim\chi^2(m),V\sim\chi^2(n) \\F=\frac{U/m}{V/n}\sim F(m,n)$

参数估计

矩估计

用样本矩来估计总体矩

$a_k=\frac1n\sum_{j=1}^nx_j^k$

最大似然估计

$L(\theta)=\prod_{i=1}^nf(x_i;\theta)$

最大化

$\frac{\text d}{\text d\theta }\ln L(\theta)=0$

评选标准

无偏

$E[\hat{\theta}(X_i)]=\theta$

渐近无偏

$\lim_{n\to\infty}E[\hat{\theta}(X_i)]=\theta$

相合

无偏或渐近无偏且

$\lim_{n\to\infty}\mathbf{Var}[\hat{\theta}(X_i)]=0$

置信区间

枢轴变量

$G=\frac{\sqrt{n}(\overline{X}-\mu)}\sigma\sim N(0,1)$

若方差已知，双侧

$\left[\overline{X}-u_{1-\frac{\alpha}{2}}\frac{\sigma }{\sqrt{n}} , \overline{X}+u_{1-\frac{\alpha}{2}}\frac{\sigma }{\sqrt{n}}\right]$

单侧

$\left[\overline{X}-u_{1-\alpha}\frac{\sigma }{\sqrt{n}} , +\infty\right)$

方差未知，用样本来估计

$\left[\overline{X}-t_{1-\frac{\alpha}{2}}(n-1)\frac{S }{\sqrt{n}} , \overline{X}+t_{1-\frac{\alpha}{2}}(n-1)\frac{S }{\sqrt{n}}\right]$

方差置信区间

$\frac{1}{\sigma^2}\sum\limits_{i=1}^n(X_i-\mu)^2 \sim \chi^2(n)$

可得

$\left[\frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{1-\frac{\alpha}{2}}(n)} , \frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{\frac{\alpha}{2}}(n)}\right]$

若方差未知则

$\left[\frac{(n-1)S^2}{\chi^2_{1-\frac{\alpha}{2}}(n-1)} , \frac{(n-1)S^2}{\chi^2_{\frac{\alpha}{2}}(n-1)}\right]$