概率论公理

我们说样本空间是无限可数的意味着其中的元素可以与正整数一一对应

样本空间$S$上的概率分布$\rm {Pr{}}$是一个从事件到实数的映射

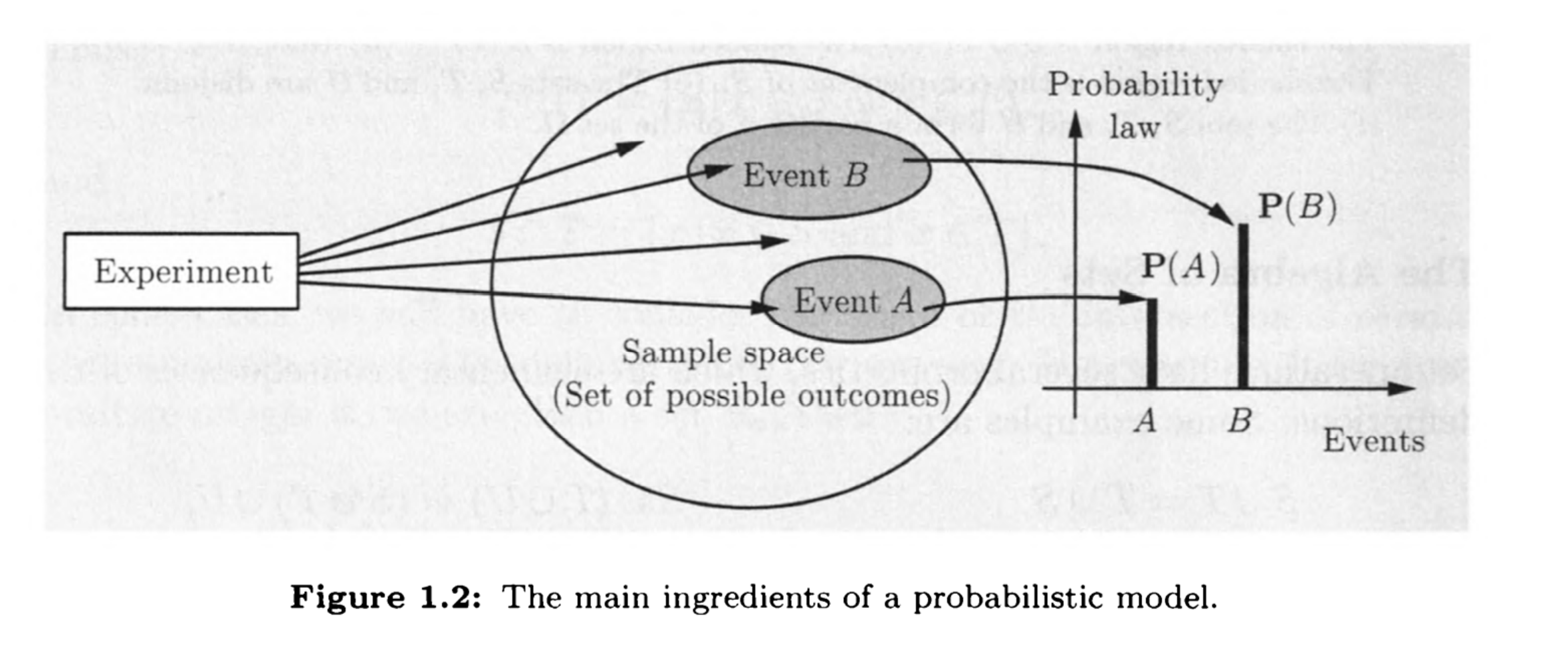
记号

将事件$\text{Pr}({A})$简记为$\text{Pr}{A}$

事件可能有无数个，如掷硬币n次H

$\forall 事件A,\text {Pr}{A}\ge0$
$\text {Pr}{S}=1$
对两两互斥的事件，有
$\text {Pr}\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}=\text {Pr}\left\{s_{1}\right\}+\text {Pr}\left\{s_{2}\right\}+\cdots+\text {Pr}\left\{s_{n}\right\}\\ \text {Pr}\left\{\bigcup_{i}A_i\right\}=\sum_i\text {Pr}\{A_i\}$

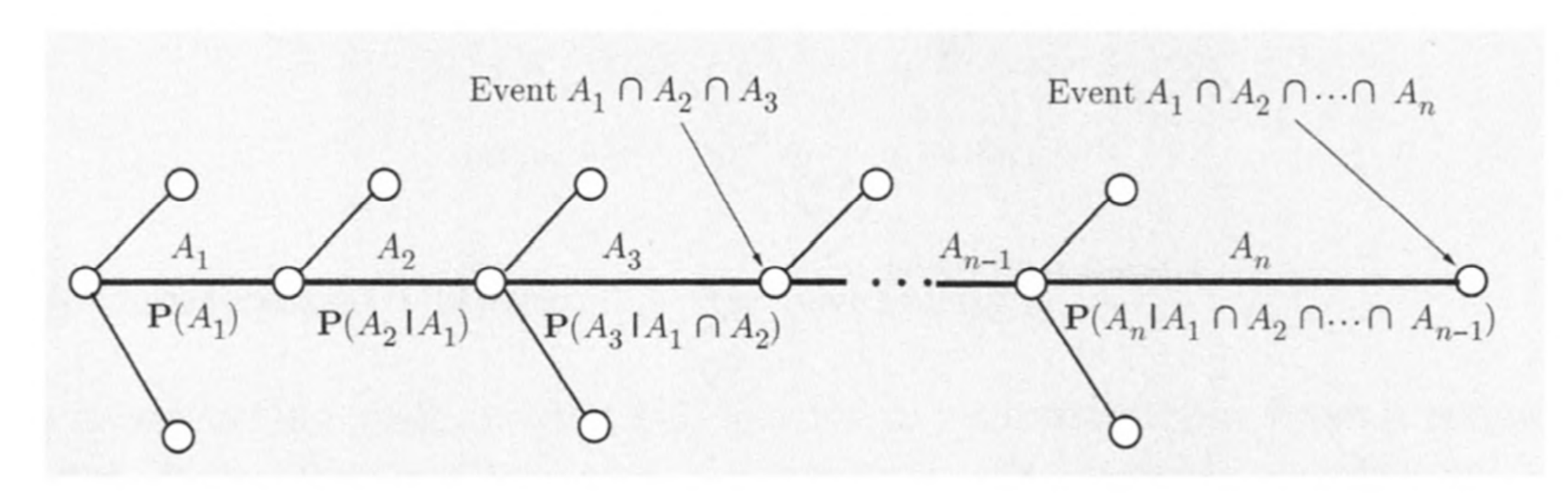
对于一个序列型的事件，可以用以下方式描述

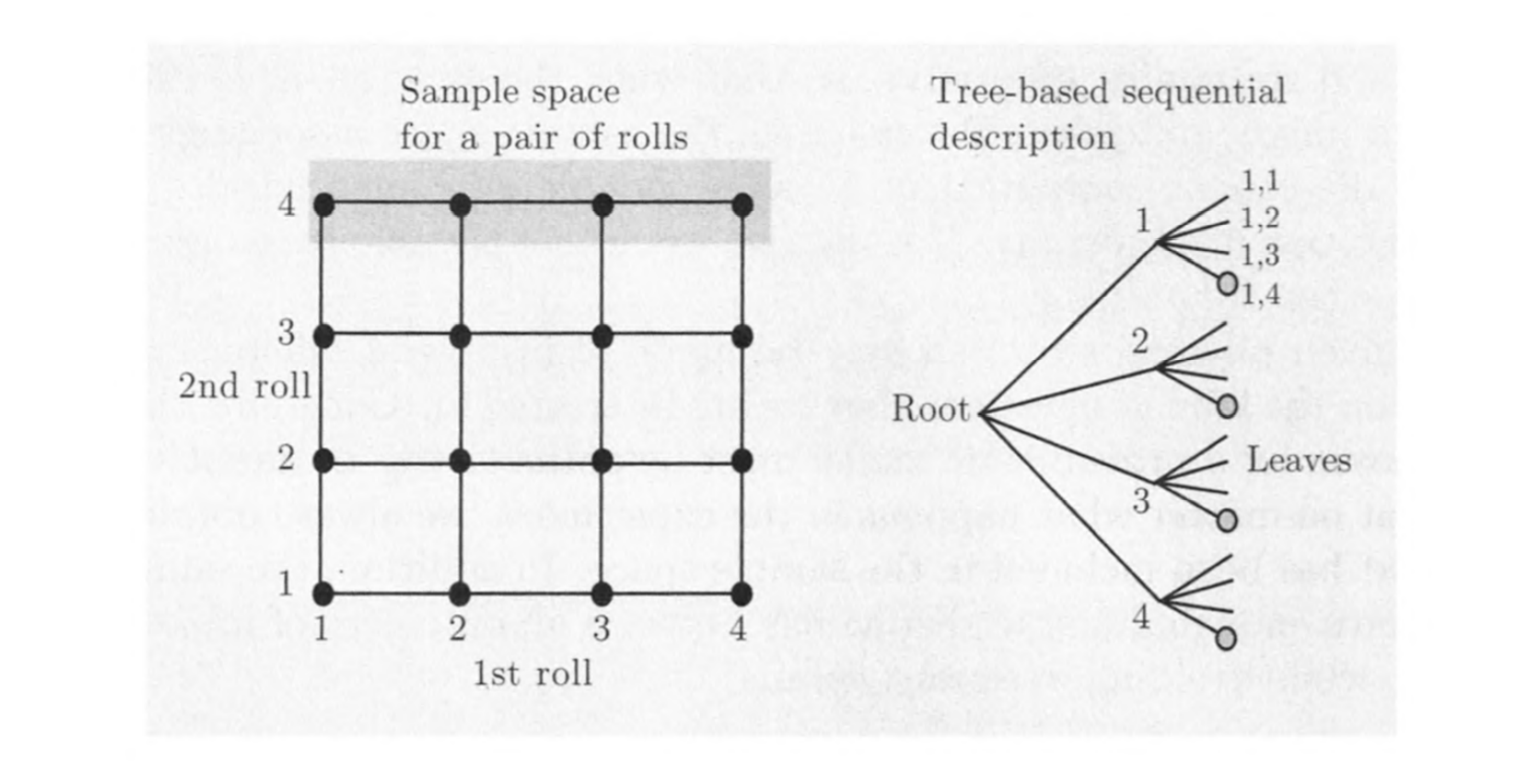
模型

为了构建模型，我们需要考虑多个因素

The choice of a model often involves a tradeof be-tween accuracy, simplicity,and tractability.

但是不论多复杂的模型，对于某个特定的事件都有确定的概率

All conceivable questions have precise answers and it is only a matter of developing the skill to arrive at them.

离散模型

对于多个等概率事件

$\text {Pr}\{A\}=\frac{\text{number of elements of }A }{n}$

连续模型

样本空间可以用图形来表示

对于样本空间为

$\Omega=[0,1]$

对于某一个值，概率为0，只有考虑长度才有意义

$\text { If } A \subset B, \text { then } \text {Pr}\{A\} \leq \text {Pr}\{B\}$

容斥

$\begin{aligned}\text {Pr}\{A\cup B\}&=\text {Pr}\{A\}+\text {Pr}\{B\}-\text {Pr}\{A\cap B\}\\&\le\text {Pr}\{A\}+\text {Pr}\{B\}\end{aligned}$ $\text {Pr}\left\{\bigcup_{i}A_i\right\}\le\sum_i\text {Pr}\{A_i\}$

由德摩根律

$\text {Pr}\{A\cup C|B\}\le\text {Pr}\{A|B\}+\text {Pr}\{C|B\}$

离散概率分布

概率分布在有限或无限可数的样本空间，则该概率分布是离散的

$\text {Pr}\{A\}=\sum_{s\in A}\text {Pr}\{s\}$

若基本事件$s\in S$的概率为

$\text {Pr}\{s\}=1/|S|$

则称为$S$上的的均匀概率分布

条件概率

已知事件 $B$发生$\text {Pr}{B}\ne 0$，事件$A$的条件概率定义为

$\text {Pr}\{A|B\}=\frac{\text {Pr}\{A\cap B\}}{\text {Pr}\{B\}}$

需要从直观角度上理解

$\text {Pr}\{A|B\}+\text {Pr}\{A^c|B\}=1$

状态转移

$\mathbf{P}\left(\cap_{i=1}^{n} A_{i}\right)=\mathbf{P}\left(A_{1}\right) \cdot \frac{\mathbf{P}\left(A_{1} \cap A_{2}\right)}{\mathbf{P}\left(A_{1}\right)} \cdot \frac{\mathbf{P}\left(A_{1} \cap A_{2} \cap A_{3}\right)}{\mathbf{P}\left(A_{1} \cap A_{2}\right)} \cdots \frac{\mathbf{P}\left(\cap_{i=1}^{n} A_{i}\right)}{\mathbf{P}\left(\cap_{i=1}^{n-1} A_{i}\right)}$

独立

若

$\text {Pr}\{A\cap B\}=\text {Pr}\{A\}\text {Pr}\{B\}$

则称事件$A$和$B$是独立的，若$\text {Pr}{B}\ne 0$，则等价于

$\text {Pr}\{A|B\}=\Pr\{A\}(与B无关)$

若对于所有$1\le i < j\le n$，有

$\text {Pr}\{A_i\cap A_j\}=\Pr\{A_i\}\Pr\{A_j\}$

则称事件$A_1,A_2,\cdots,A_n$两两独立

若对这些事件的每一个$k$子集${ A{i_1},A{i2},\cdots,A{i_k}}$，其中$2\le k\le n$且$1\le {i_1}< {i_2}< \cdots< {i_k}\le n $，有

$\Pr\{ A_{i_1}\cap A_{i_2}\cap \cdots\cap A_{i_k}\}=\Pr\{ A_{i_1}\}\Pr\{ A_{i_2}\}\cdots\Pr\{ A_{i_k}\}$

则称这些事件相互独立

条件独立

$\text {Pr}\{A\cap B|C\}=\text {Pr}\{A|C\}\text {Pr}\{B|C\}\\ \Leftrightarrow\text {Pr}\{A| B\cap C\}=\text {Pr}\{A|C\}$

In words, this relation states that if is known to have occurred,the additional knowledge that B also occurred does not change the probability of A.

考虑事件A为第一次掷为H，B为第二次H，C为两次结果不同

$\text {Pr}\{A\cap B|C\}=0\\\text {Pr}\{A|C\}=\text {Pr}\{B|C\}=\frac12$

所以独立不代表条件独立

$\text {Pr}\{A\cap B\cap C\}=0$

则A，B两个独立事件不条件独立

全概率公式

将样本空间$\Omega$划分为两两独立的$n$个事件，且

$\bigcup_iA_i=\Omega$

则

$\Pr\{B\}=\sum_{i=1}^n\Pr\{B|A_i\}\Pr\{A_i\}$

贝叶斯定理

由

$\Pr\{A\cap B\}=\Pr\{A|B\}\Pr\{B\}=\Pr\{B|A\}\Pr\{A\}$

得

$\Pr\{A|B\}=\frac{\Pr\{B|A\}\Pr\{A\}}{\Pr\{B\}}$

对于$\Pr{B}$，因为可以划分，故

$\Pr\{B\}=\Pr\{B|A\}\Pr\{A\}+\Pr\{B|\overline{A} \}\Pr\{\overline{A} \}$

所

$\Pr\{A|B\}=\frac{\Pr\{B|A\}\Pr\{A\}}{\Pr\{B|A\}\Pr\{A\}+\Pr\{B|\overline{A} \}\Pr\{\overline{A} \}}$

贝叶斯定理常常用来由果导因，如抗原阳性是否代表感染新冠

$\Pr\{A_i|B\}=\frac{\Pr\{B|A_i\}\Pr\{A_i\}}{\Pr\{B|A_1\}\Pr\{A_1\}+\dots+\Pr\{B|A_n \}\Pr\{A_n \}}$

其中$\Pr{A_i|B}$为后验概率，$\Pr{A_i}$是先验概率

计数

分类加法计数原理，同一个阶段的不同方法可以相加

有N个阶段每个阶段有$n_i$个方式，则总方式为

$n_1n_2\cdots n_N$

排列数

$k-\text{permutations}=\frac{n!}{(n-k)!}$

组合数

$\left(\begin{array}{l}n\\k\end{array}\right)=\frac{n!}{(n-k)!k!}$

多项式定理

将n个元素分为$k$类，其中各为$n_i$个

$C_{n}^{n_{1}} C_{n-n_{1}}^{n_{2}} \ldots C_{n-n_{1}-\ldots-n_{k-1}}^{n_{k}}=\frac{n !}{n_{1} ! n_{2} ! \ldots n_{k} !}$ $\left(x_{1}+\ldots+x_{k}\right)^{n}=\sum_{n_{1}+\ldots+n_{k}=n}\left(\begin{array}{ccc} & n & \\ n_{1} & \ldots & n_{k} \end{array}\right) x_{1}^{n_{1}} x_{2}^{n_{2}} \ldots x_{k}^{n_{k}}$