基本概念
傅里叶定律
导热热流密度的大小与温度梯度的绝对值成正比其方向与温度梯度的方向相反
从而可以导出热导率
导热微分方程
假设热导率为常数
$\Phi$为内热源强度,定义热扩散率,也称导温系数
边界条件
第一类
边界温度为常数,为恒壁温边界条件
第二类
给定法线方向的温度变化率,为恒热流边界条件
若$q_w=0$则为绝热条件
第三类
给出传热系数$h$和温度$t_f$,由牛顿冷却定律和傅里叶定律,可得对流边界条件
热电比拟
热阻
平壁一维导热热阻
对流换热热阻
时间响应,在数学上就是系统动力学方程的解
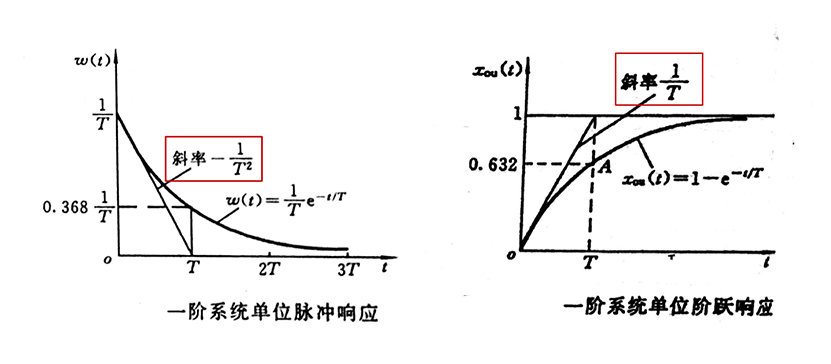
$t_s$为调整时间$3T\to 95\%,4T\to98\%$
一阶系统在阶跃输入下达到稳态的 $(1-\Delta)$ 时所用的时间 ( $\Delta$ 为容许误差)
$t_s$ 反应系统的快速性,T越大,调整时间越大,响应速度越慢
对 $G(s)=\frac{\omega_n^2}{s^2+2\xi\omega_n s+\omega_n^2}$ 来说:
特征方程:${s^2+2\xi\omega_n s+\omega_n^2}$
特征根:$s=\xi\omega_n\pm\omega_n\sqrt{1-\xi^2}$

上升时间$t_r$ :系统第一次到达稳态的时间
峰值时间$t_p$:系统第一次到达峰值的时间
最大超调量$M_p$:(峰值 - 稳态)/峰值%
调整时间$t_s$,当 $0<\xi<0.7$ 时
- $\xi$ 主要与震荡性(稳定性)正相关,$\omega_n$ 主要与快速性正相关。
- 系统的响应速度往往与震荡性能之间是矛盾的
对于一阶惯性系统,输入正弦信号$\sin(\omega t)$
分解
根据时移特性拉氏反变换,得到
所以稳态之后的信号也为正弦,幅值和相位的求法是把$s=j\omega$带入传递函数
从而有时频特性和相频特性
根据上面的每个$\omega$的幅值和相位可以确定一个点,绘制纵$0\to \infty$的曲线即为奈奎斯特图。
用极限的方法
或者复数相乘,模相乘辐角相加原理,用常见的叠加得到
即对数坐标图,纵坐标取对数,横坐标采用10倍频程比值缩放$\text{(dec)}$
(坐标轴仍任显示原值,只是计算斜率时使用)
斜率
可以直接用斜率近似计算,也可以利用
直接计算关键点
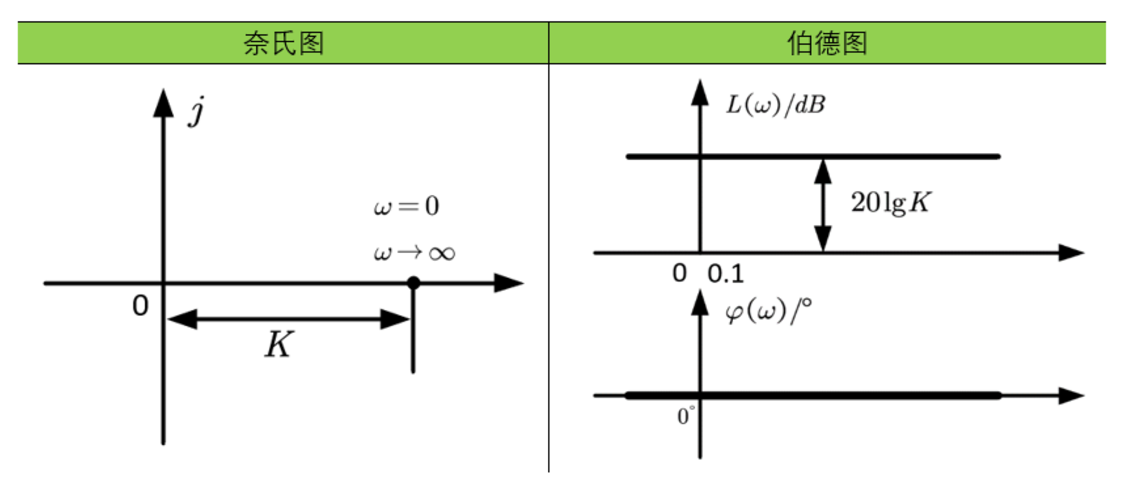
比例环节的频率特性是与频率无关的常数,在奈奎斯特图上表现为实轴上一个点,在伯德图中表现为与频率无关的两条直线
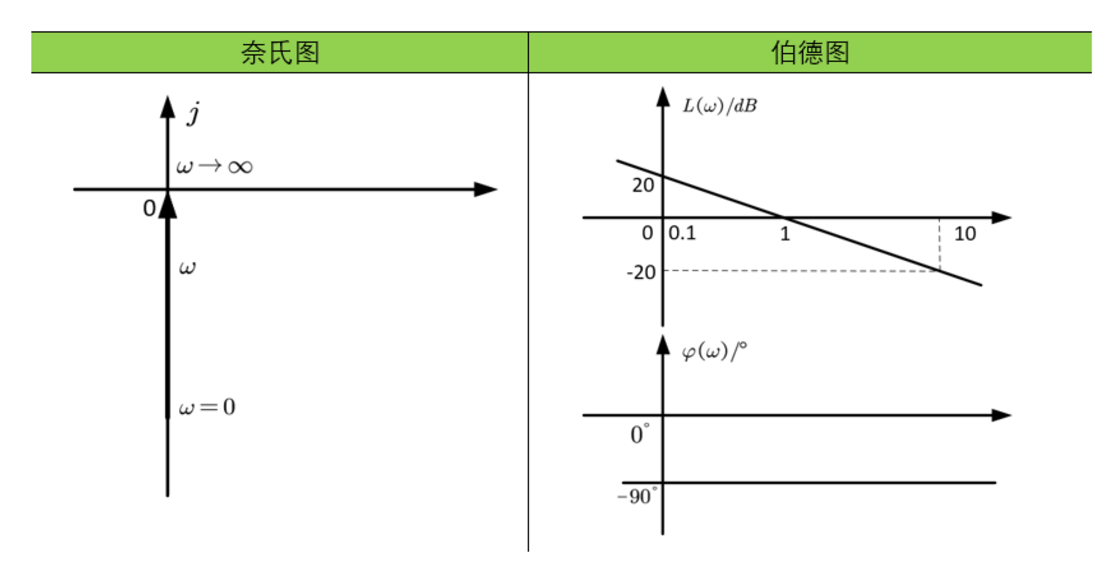
积分环节的输出量是其输入量对时间的积分。奈奎斯特图是虚轴上从负无穷到原点的一条直线,相角恒为$-90^\circ$。对数幅频特性是一条$[-20]$斜率的直线,相角保持$-90^\circ$不变。
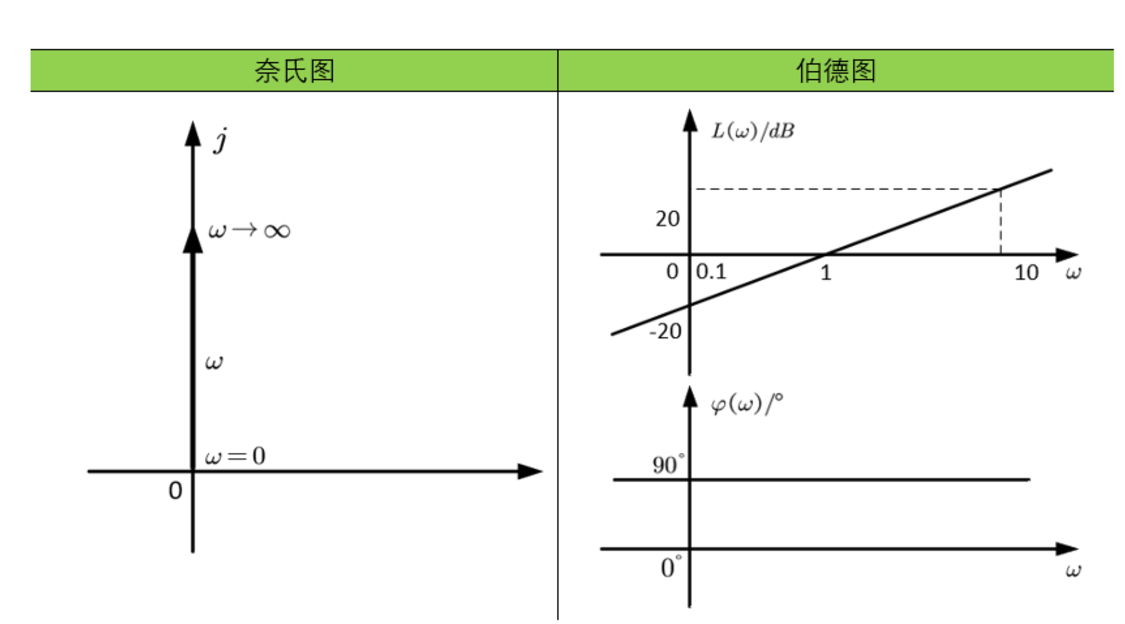
微分环节的输出量是其输入量对时间的微分。奈奎斯特图是虚轴上从原点到正无穷的一条直线,相角恒为90°。对数幅频特性是一条$[+20]$斜率的直线,相角保持90°不变。
惯性环节的奈奎斯特图是一个半圆(数学上可证明)。在伯德图中,转折频率之后的对数幅频特性为一条$[-20]$斜率的直线(近似,实际上在转折频率处衰减了3dB)。相角变化从0°到-90°。
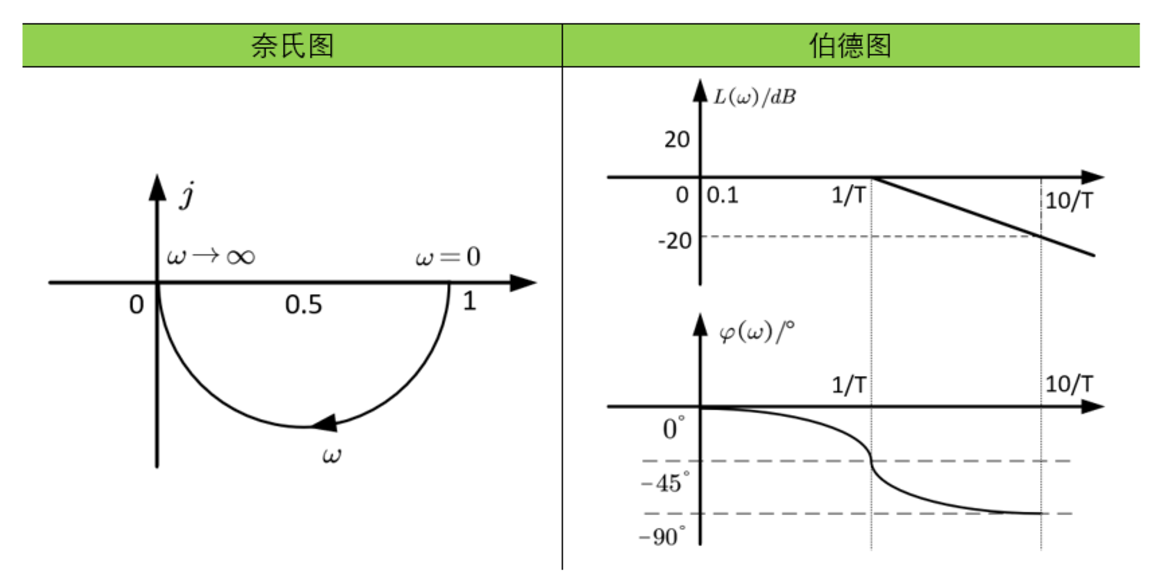
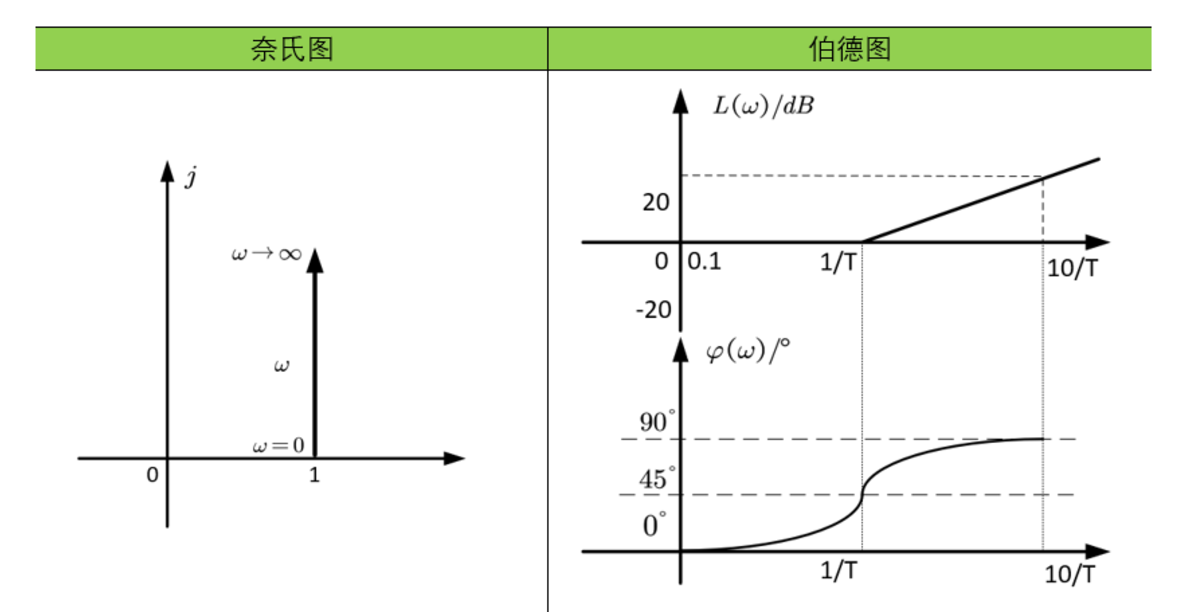
一阶微分环节的输出量取决于其输入量及一阶微分。它的奈奎斯特图相当于微分环节的图像向右平移了一个单位。它的对数频率特性与惯性环节相差一个负号,所以它们的对数频率特性关于横轴对称。
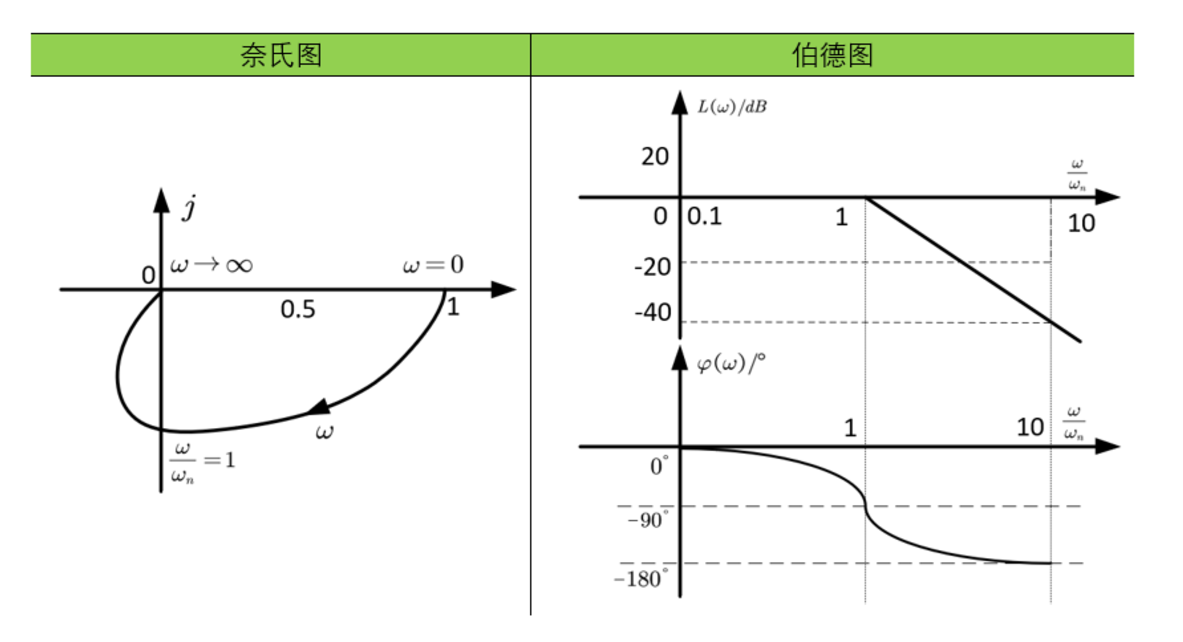
振荡环节的图像应该是由不同阻尼比的情况下组成的一簇曲线,它们的奈奎斯特图起于实轴1处的点,终于原点。转折频率后的模值以40dB的速度衰减。相角从0°变化到-180°。
控制系统在任何足够小的初始偏移下,过渡过程随着时间的推移逐渐衰减为0,则为稳定系统
对典型系统求单位脉冲响应,对得到的时域表达式进行分析得到
闭环传递函数的极点全部都在$s$平面的左半平面
根据根与系数的关系,可以得到劳斯阵列

其中有递推公式
若计算得到的第一列全为正数则稳定,否则符号变化几次就有几个根在左半平面
对于三阶多项式,可以得到
开环传递函数$G(s)H(s)$从$-\infty j\to \infty j$包围$(-1,j0)$点的圈数
$G(s)H(s)$是实系数有理分式函数,由于对称性,一般只绘制$0\to \infty j$的图线
辐角原理,参考
https://blog.csdn.net/weixin_46664967/article/details/113208585
$F(s)$绕平面原点的圈数只和$F(s)$被闭合曲线$ Γ$(取成整个右半平面) 包围$F(s)$的零点和极点的代数和有关
R:R等于$ΓGH $逆时针包围F(s)平面上点 $(-1 , j0)$的圈数
P:开环传递函数在右半平面内的极点数,P是已知的
Z:闭环传递函数在右半平面内的极点数,若Z = 0 系统稳定
通过平移即可得到
作出开环系统的奈奎斯特曲线
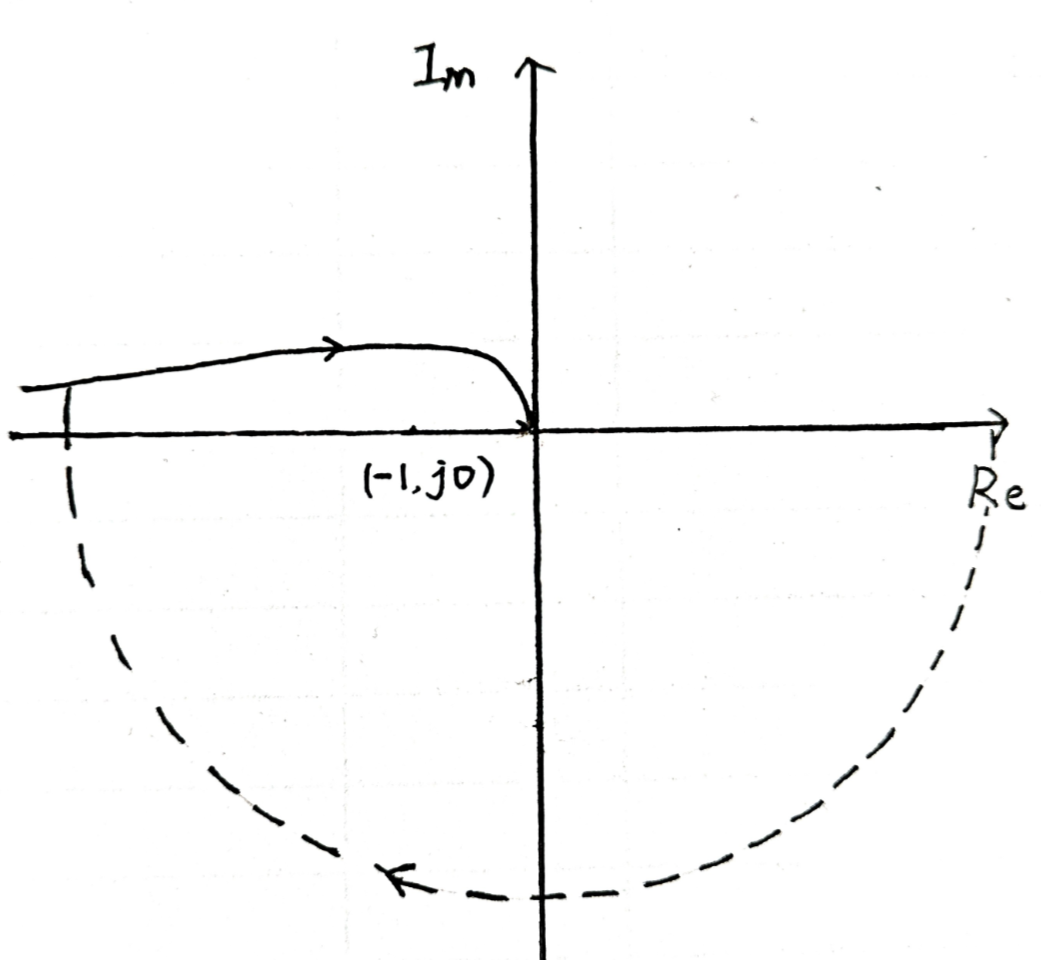
若不完整需要补圆
若有$(1/s)^v$项,则以奈奎斯特曲线的起始位置为起点,逆时针画 $v\times 90°$ 半径无穷大的圆弧,但该圆弧的方向为顺时针
在 (-1,j0) 左侧 正穿越 的次数 (从上往下) ,N-为¥左侧 负穿越的次数 (从下往上)
R 表示开环系统 G(s)H(s) 逆时针绕点(-1,j0)的圈数,等价于1+G(s)H(s) 顺时针绕原点的圈数
N+ 表示点 (-1,j0) 左侧正穿越的次数(从上向下穿越)
N- 表示 点 (-1,j0) 左侧负穿越的次数(从下向上穿越)
只看左侧
P为开环传递函数在右半平面极点数
理想输出和实际输出量之差为误差$e(t)$,象函数为$E(s)$,误差信号的稳态分量(静态误差),记作$e_{\text{ss}}$
输入信号和反馈信号比较后的信号$\varepsilon (t)$称为偏差
考虑偏差趋近于0,理想输出传递回来偏差为0,故
故
对于单位反馈系统,误差等于偏差
所以误差传递函数为
根据终值定理
对于非单位反馈系统
稳态偏差为
一般$H(s)$为常数,故
对于单位阶跃响应
稳态偏差为
可以定义静态误差系数为
对于$0$型而言
对于高于$\rm I$型的系统,分母$s\to 0$
对于单位斜坡输入
同理对于单位加速度输入,也有静态加速度系数
总结如下表
| 系统类别 | 单位阶跃 | 等速输入 | 等加速输入 |
|---|---|---|---|
| 0型系统 | $\frac1{1+K}$ | $\infty$ | $\infty$ |
| I型系统 | $0$ | $\frac1K$ | $\infty$ |
| II型系统 | $0$ | $0$ | $\frac1K$ |
忽略输入,只计算干扰
之后可以用叠加原理计算总误差
需要把$x_o(t)$用数学的方式表达
奇异函数
指数信号的因子是复数
一个复指数信号可以分解为实部$\cos$和虚部$\sin$,满足
借助这个关系就能方便的对正弦信号进行升维到复数域,让信号理论更加优雅,便于分析
有重要的两个参数:振幅和相位,复数相乘,模相乘辐角相加
对于单输入单输出的控制系统,我们用微分方程来描述
但解微分方程太过繁琐,引入复数后就可以用拉氏变换来简化
由微分性质得到
若零初始条件则有
这样方程就不含微分项,将微分方程变成了代数方程
积分
时移
初值定理
终值定理
求解出的频域信号需要转换回时域
| $f(t)$ | $L[f(t)]$ | $f(t)$ | $L[f(t)]$ |
|---|---|---|---|
| $1$ | $\frac1s$ | $t$ | $\frac{n!}{s^{n+1}}$ |
| $e^{at}$ | $\frac1{s-a}$ | $\sin\omega t$ | $\frac{\omega}{s^2+\omega^2}$ |
| $\cos\omega t$ | $\frac{s}{s^2+\omega^2}$ | $te^{-at}$ | $\frac1{(s+a)^2}$ |
由分解定理,一般常见的有理分式
可以分解为不同单极点$(e^{-at})$的形式,和共轭复数极点$(\sin/ \cos)$
根据上面的分析,我们可以将系统里面常见的组件抽象成频域里面的函数
假设系统有极点,复零点$(s^2+w^2)$,极点,复极点,则传递函数可以写成
可以看出有多种环节,如比例环节
所以分母系数$s$上面次数代表为$v$阶系统
理想微分
一阶微分
二阶微分
阻尼
故一阶惯性为
二阶振荡

自动控制,就是在没有人为干预的条件下,使目标的某些物理量准确地按照预期变化

按照有没有反馈测量装置分为闭环系统和开环系统
例如简单的电机转速控制系统根据电压来控制转速,是开环
还分为模拟控制系统和数字控制系统;若保持恒定则为恒值调节系统,若变化则为随动系统。
可用线性微分方程描述的称为线性控制系统,反之为非线性系统。
执行元件 Actuator Device that provides motive power to the process
比较元件 Comparator Computes the difference between the desired and actual output
控制器 Controller Device that computes the control signal. Composed of comparator
and compensator
输出 Output The output of the system to be controlled
设备 Plant Combination of the actuator and the system under control
控制对象 Process System or device, whose output is to be controlled
参考输入 Reference input The desired output of the system. Also called set point or input传感器 Sensor Device that detects and measures some physical effect and generates a
signal proportional to the effect
传递函数 Transfer function Ratio of the transforms of system output and input. That is,
the transform of the input multiplied by the transfer function is the output in the
transform domain
还有放大元件,校正元件(反馈校正和串联校正)
World is the core class that enables you to interact with the simulator in an easy and modular way. It takes care of many time-related events such as adding callbacks, stepping physics, resetting the scene, adding tasks, etc. The World class is a Singleton which means ==only one World can exist== while running Omniverse Isaac Sim. Query the World for information about the simulation from different extensions.
1 | from omni.isaac.examples.base_sample import BaseSample #boiler plate of a robotics extension application |
The Dynamic Control extension is a set of utilities to control physics objects. It provides opaque handles for different physics objects that remain valid between PhysX scene resets, which occur whenever play or stop is pressed.
用于运动控制
A world contains an instance of a Scene, think about it as a scene management class that manages the assets of interest in the USD stage. It provides an easy api to add, manipulate and inspect different USD assets in the stage as well as setting its default reset states. Many of the object classes available which could be added to a Scene usually takes an already existing USD prim in stage or creates a new USD prim, thus providing an easy way to set/ get its common properties.
1 | world.scene.add_default_ground_plane() # adds a default ground plane to the scene |
The Task class in omni.isaac.core provides a way to ==modularize== the scene creation, information retrieval, calculating metrics and creating more complex scenes with more involved logic.
GPU并行仿真
This class provides a way to set up a task in a scene and modularize adding objects to stage, getting observations needed for the behavioral layer, calculating metrics needed about the task, calling certain things pre-stepping, creating multiple tasks at the same time and much more.
一堆关节构成
An articulated robot is ==a robot with rotary joints== (e.g: a legged robot, a manipulator or a wheeled robot). In omni.isaac.core extension in Omniverse Isaac Sim there exists an Articulation class which enables the interaction with articulations that exists in a USD stage in an easy way.
Robots are constructed of physically accurate articulated joints.
High-level wrapper to deal with prims (==one or many==) that have the Root Articulation API applied and their attributes/properties
This class wraps all matching articulations found at the regex provided at the prim_paths_expr argument
匹配多个
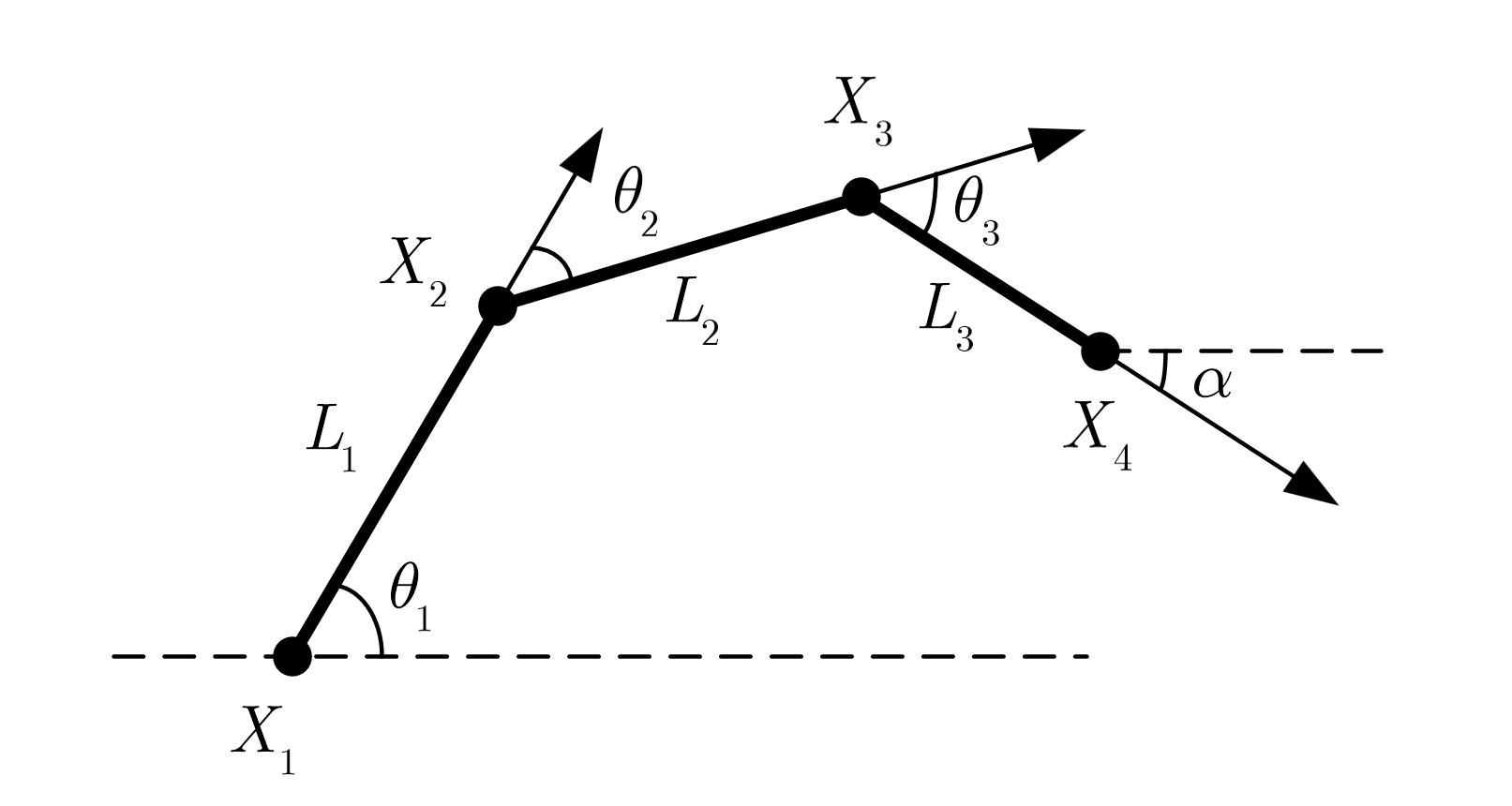
所以可以控制三个关节的转角来使得机械臂末端$X_4$运动到
求解过程
利用余弦定理求解$\theta_1,\theta_2$
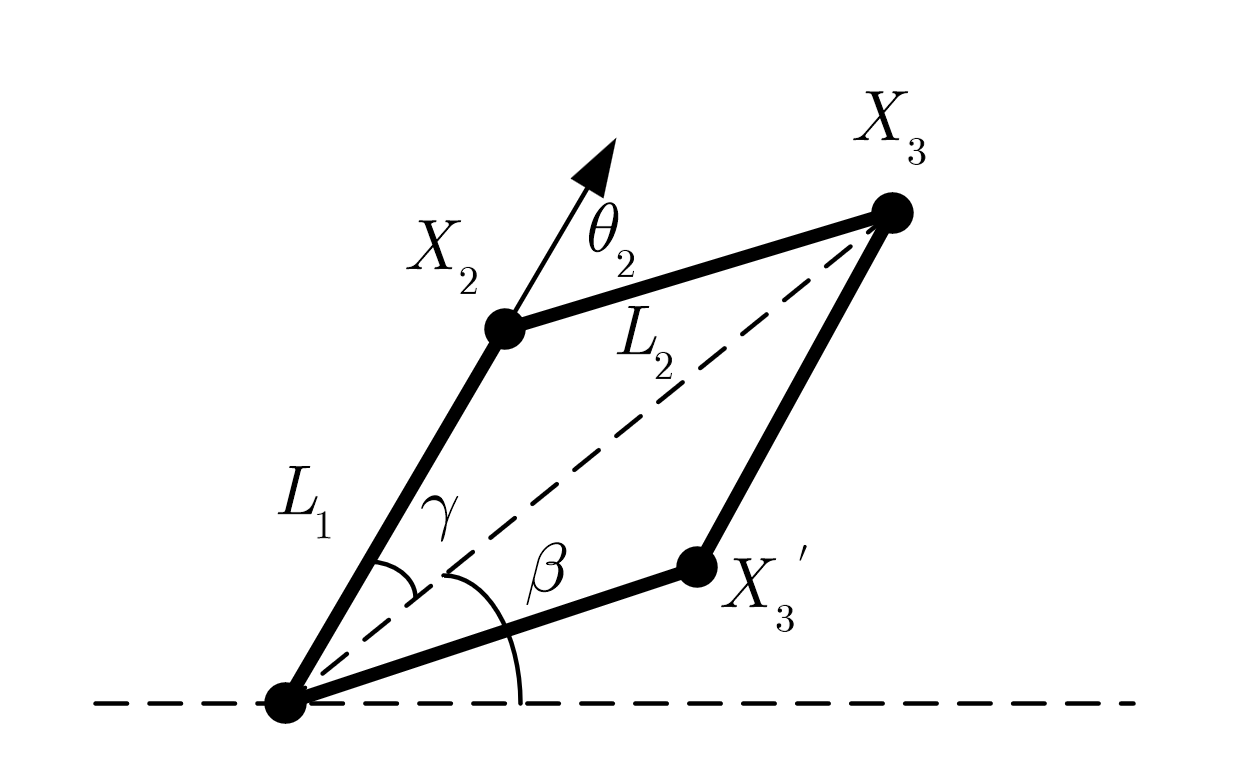
在三角形内使用余弦定理
所以
由于自由度受限,故空间内机械臂规划只考虑
$\alpha=90^\circ$,即垂直抓取的情况,考虑俯视图
砖块处在相对$X_0$,$(x,y)$的位置,位姿为$\theta$
云台转角为$\theta_0$,夹爪的转角为$\theta_4$
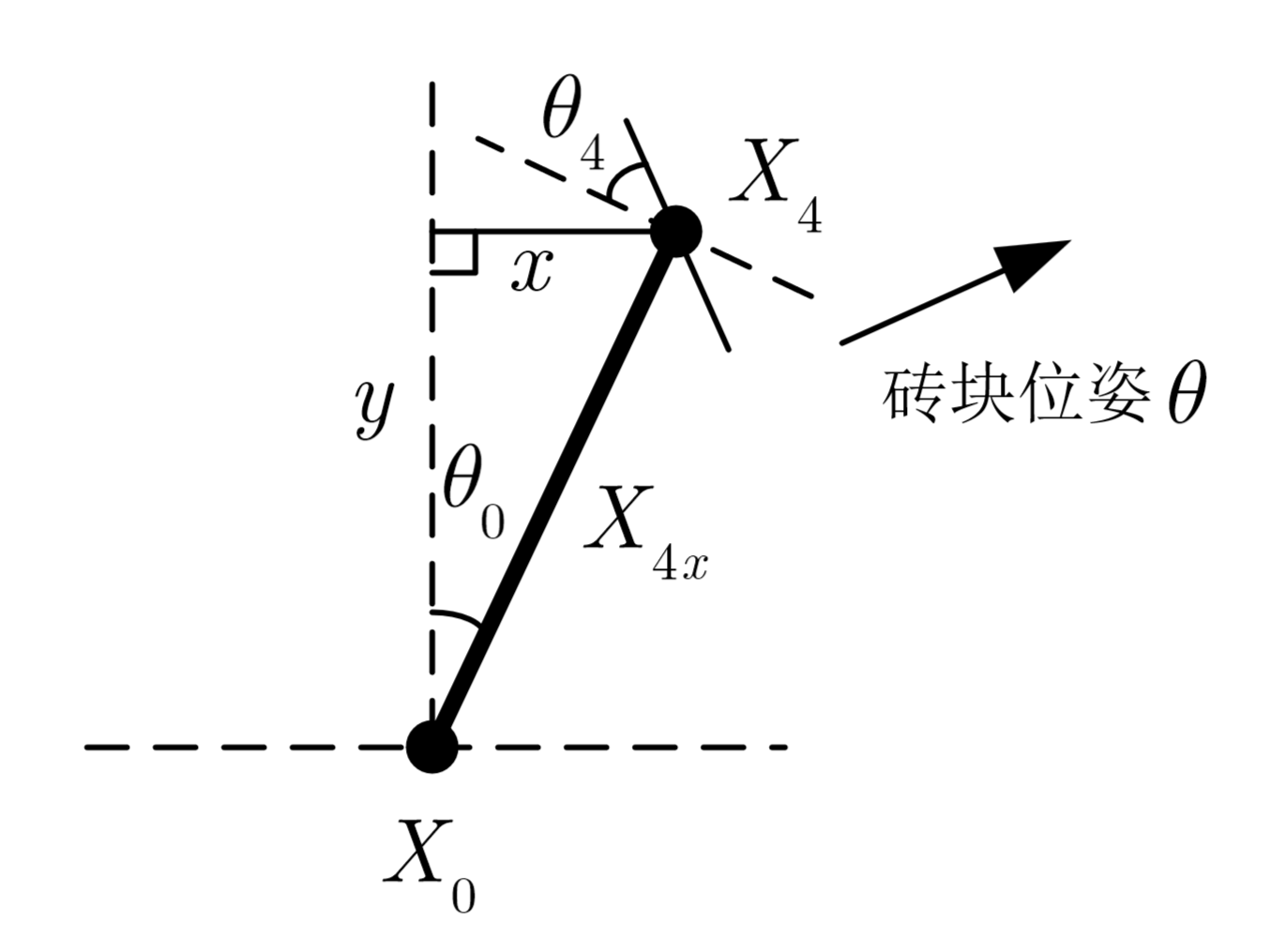
通过这些方程可以求解出$\theta_0,\theta_1,\theta_2,\theta_3,\theta_4$
再通过$\theta_5$控制夹爪的张开与夹紧就可实现完整的抓取
贝塞尔曲线具有良好的空间连续性,采用空间贝塞尔曲线的路径,不仅可有效增加空间曲线的平滑性并可通过更改控制点修改局部速度及加速度值,同时可通过控制点修改曲线形状,并且具有较高的计算效率。
Bernstein基函数
Bezier曲线的表达式
在计算机图形学常用De Casteljau来对贝塞尔曲线进行求值
算法利用如下递归表达式来实现
轨迹设计
由于我们需要将砖块一块一块砌筑,并且需要保证尽可能垂直向下放置砖块,从而能利用榫卯结构让两砖块之间能够贴合且不发生碰撞,所以为简单起见采用三个点作为控制顶点,分别是机械臂末端起点,终点,和终点正上方$d$处的控制点,利用贝塞尔曲线的端点性质,保证接近终点时速度一定垂直向下。
由于对于轨迹上的任意一点$(x,y,z,\alpha)$,我们需要确定$\alpha$的取值使得和机械臂的四个关节角度$(\theta_0,\theta_1,\theta_2,\theta_3)$一一对应从而求解,我们采用一种启发式的方式来设定$\alpha_t$,设当前进度为$t,t\in[0,1]$,则
再利用搜索的方式找到离$\alpha_t$最近且使得逆运动学有解的$\alpha$,从而求解四个关节角度。
由于当关节角度$\theta=0$时,存在奇异点,末端执行器的一点微小变化会导致机械臂角度剧烈变化,产生震荡,所以在保证终点处不会存在角度为$0$后,我们可以对求解出角度小于某个设定阈值的部分不采用这段轨迹,并对关节角度利用线性插值的方式来生成新轨迹,使得轨迹更加稳定。
但由于局部突然用线性插值来替代,导致轨迹不够平滑,衔接处加速度过大,所以采用Savitzky-Golay滤波对新轨迹进行平滑,从而得到更加自然,加速度更小的轨迹
we need to lay bricks one by one and ensure that they are placed as vertically as possible to utilize the mortise and tenon structure to ensure that the bricks can fit together without colliding, three points are chosen as control vertices for simplicity. These points are the starting point of the robotic arm end effector, the endpoint, and a control point $d$ directly above the endpoint. Using the endpoint property of the Bézier curve, it ensures that the speed is strictly vertical as it approaches the endpoint.
For any point $(x, y, z, \alpha)$ on the trajectory, we need to determine the value of $\alpha$ so that it corresponds to the four joint angles $(\theta_0, \theta_1, \theta_2, \theta_3)$ of the robotic arm. We use a heuristic method to set $\alpha_t$. Let the current progress be $t, t \in [0, 1]$, then
Then, by searching for the closest $\alpha$ to $\alpha_t$ that allows for solvable inverse kinematics, the four joint angles can be solved.
Since there are singular points when the joint angle $\theta = 0$, a slight change in the end effector will cause drastic changes in the angles of the robotic arm, resulting in oscillations. Therefore, after ensuring that there are no angles equal to $0$ at the endpoint, we can discard the portion of the trajectory where the angles are less than a certain threshold and use linear interpolation for the joint angles to generate a new trajectory, making the trajectory more stable.
However, abruptly replacing parts of the trajectory with linear interpolation makes it less smooth, with excessive acceleration at the junctions. Hence, we use Savitzky-Golay filtering to smooth the new trajectory, resulting in a more natural trajectory with lower acceleration.
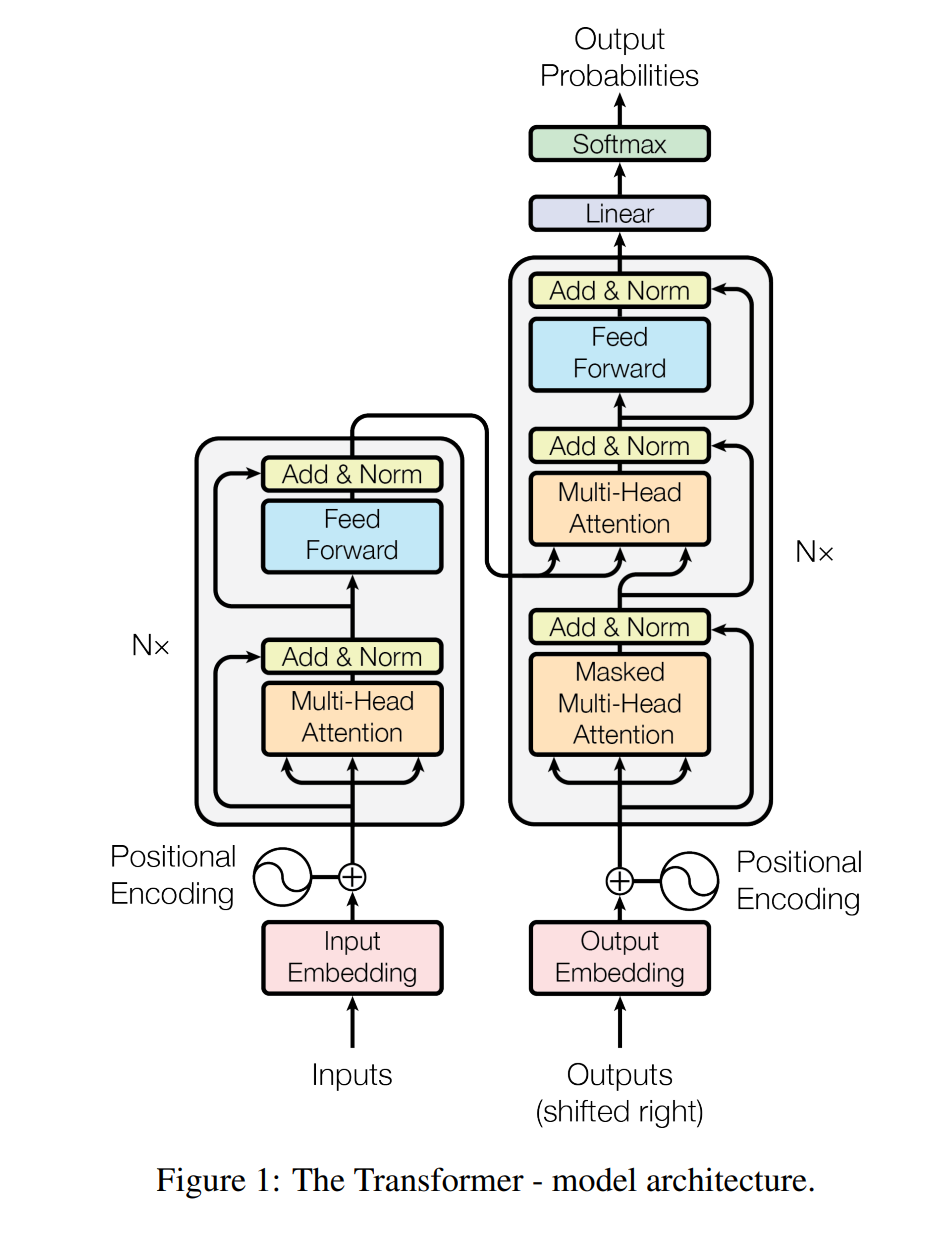
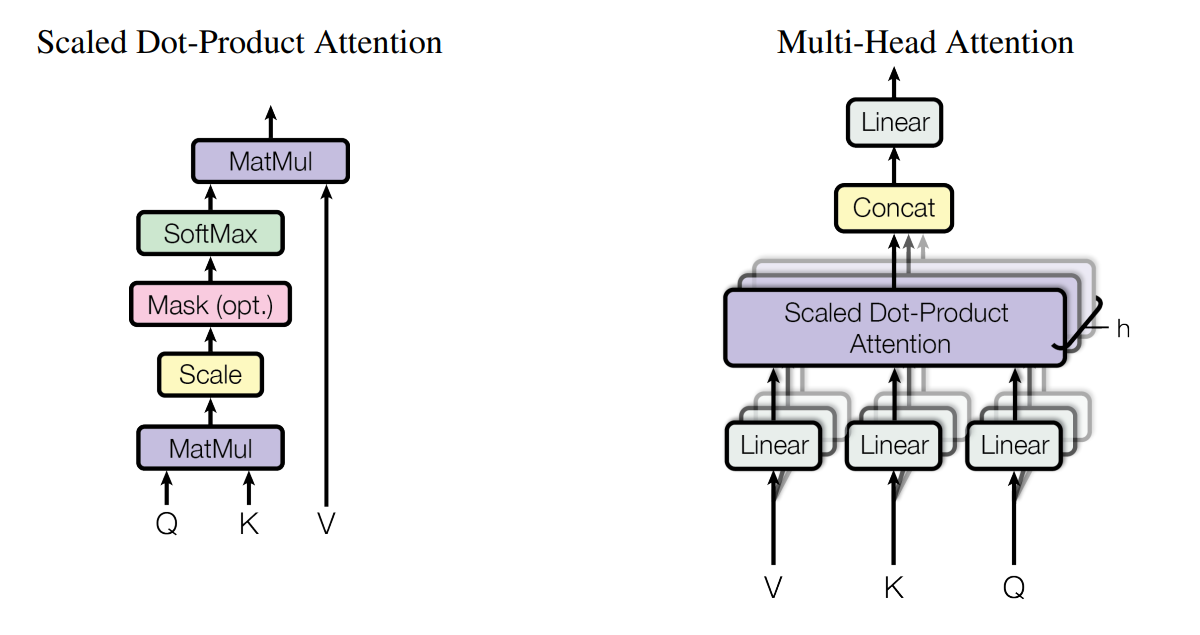
何为自注意力,就是输入为自己
利用$FC$层编码信息后
利用余弦相似度进行判断
利用$\text{softmax}$得到概率分布,最后得到输出
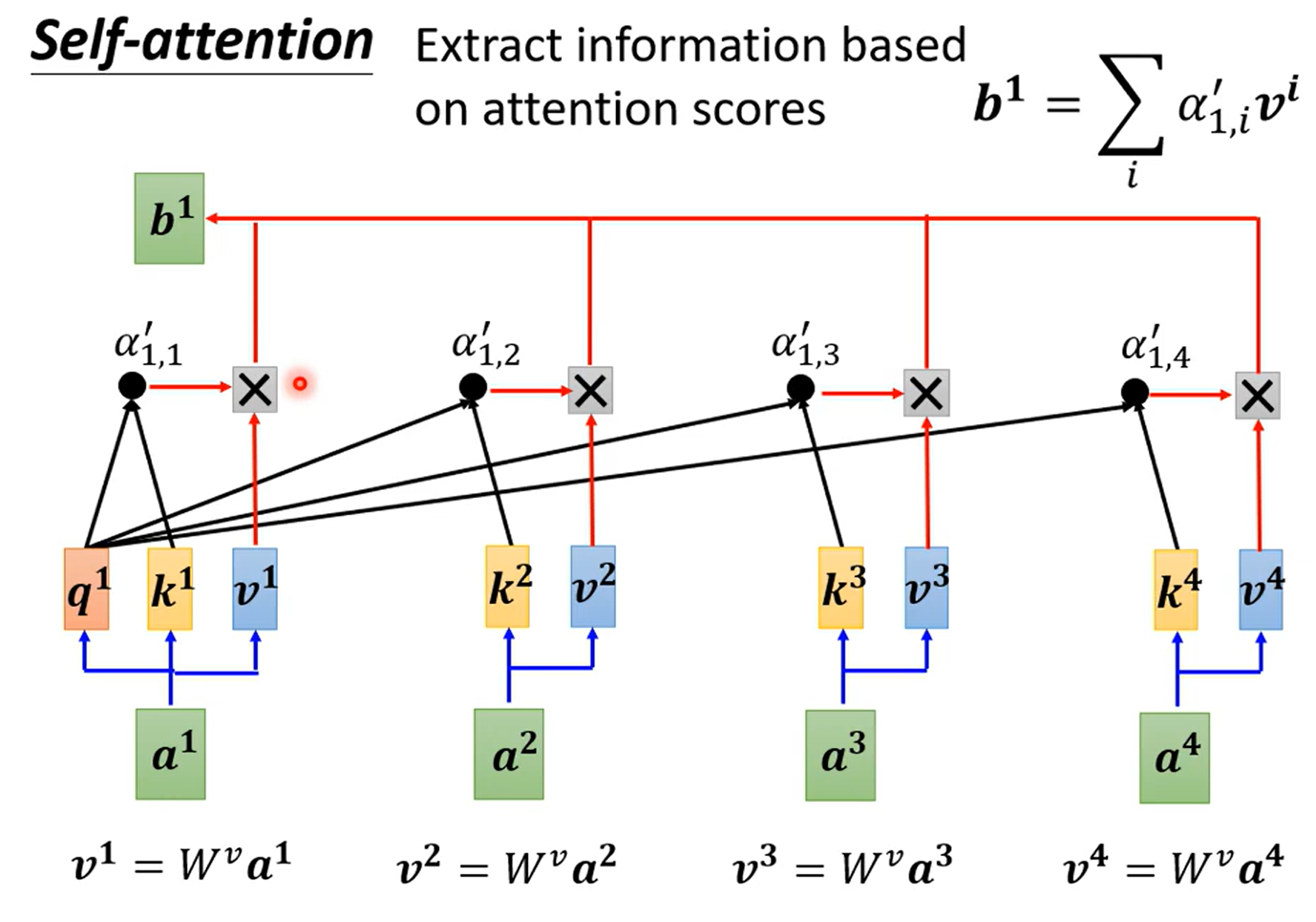
输出为类似加权平均的形式,是$Q$的编码结果
其中$W$为权重矩阵,通过训练得出
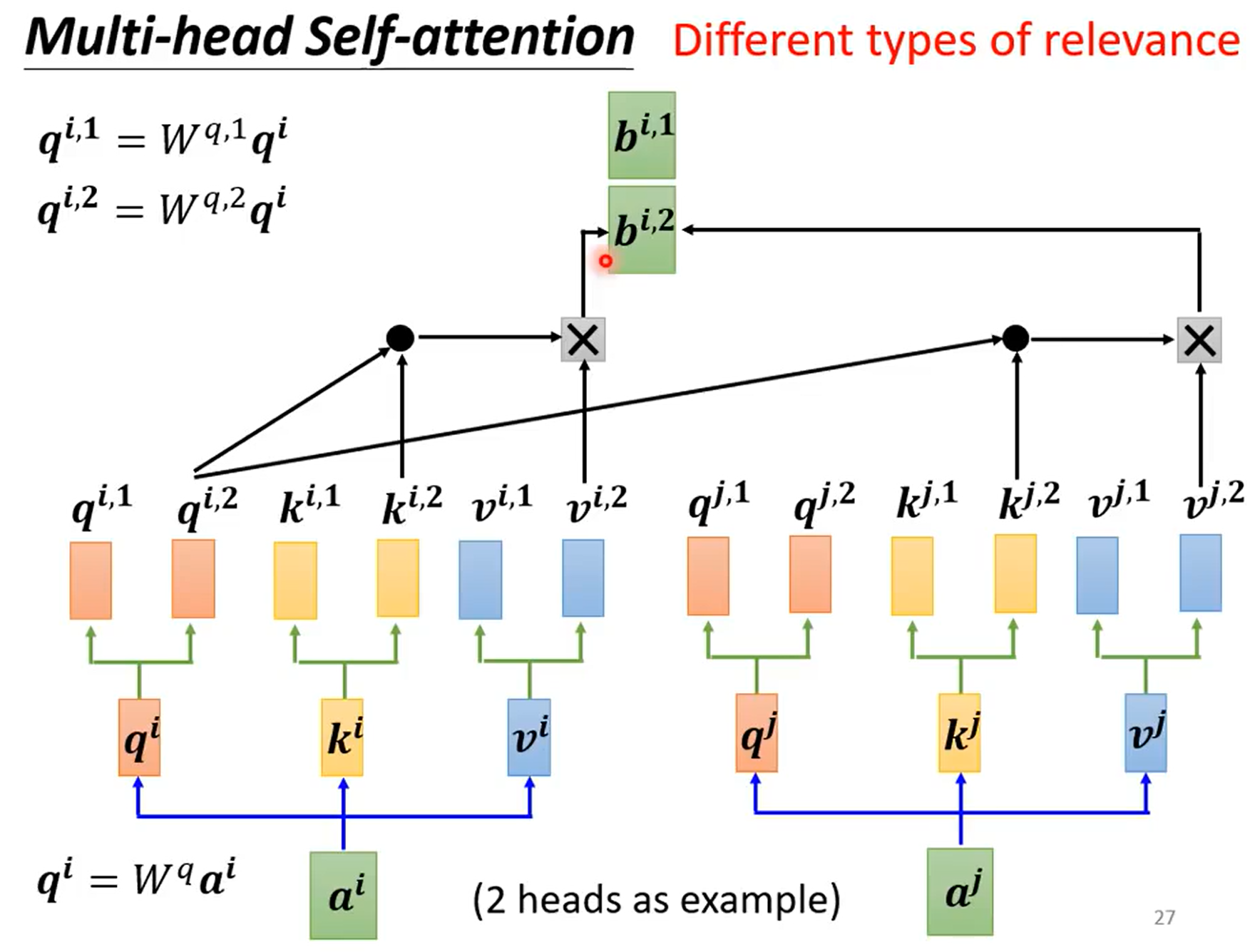
相关性也有不同的种类
利用$FC$将数据进行特征分离,并行$h$头
为了学习序列的位置信息,使用位置向量$e^i$
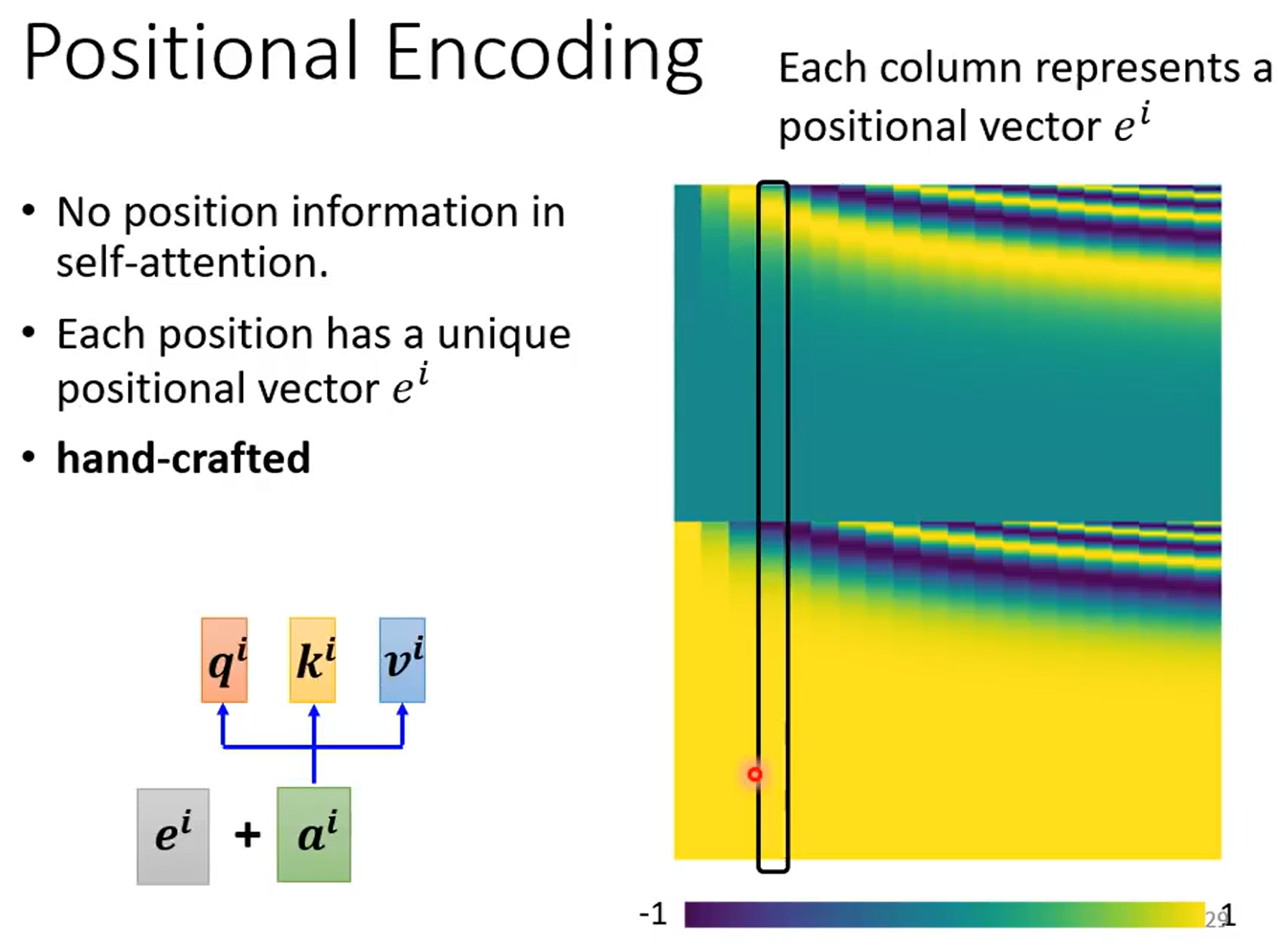
手工设定,或者直接学习
对不同的特征计算
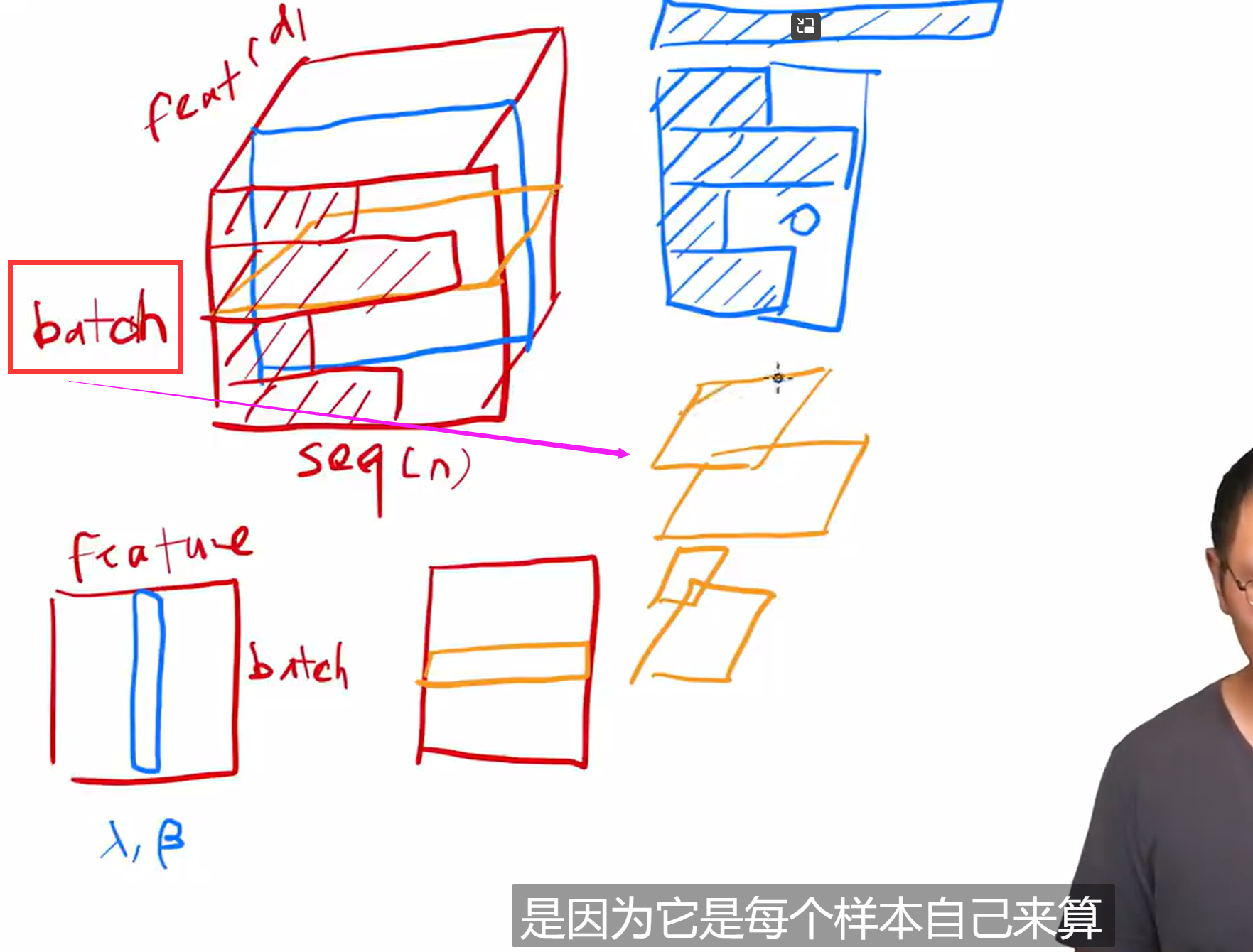
常常对最后一个维度进行,对多头即为
训练的过程中始终保留了原始信息,还增加了网络中获取的新知识
$F(x_l,W_l)$为残差
由损失函数的梯度计算结果可知,网络在进行反向传播时,错误信号可以不经过任何中间权重矩阵变换直接传播到低层,一定程度上可以缓解梯度弥散(梯度消失)问题(即便中间层矩阵权重很小,梯度也基本不会消失)
其中前馈层为
这个前馈层的作用是引入非线性映射$(\rm ReLU)$,通过两个线性变换和激活函数,对输入进行复杂的非线性变换。这有助于模型学习更加复杂的函数关系。在 Transformer 模型中,每个位置都有独立的前馈层,这使得模型能够在不同位置学习不同的表示。
将Encoder编码的信息进行解码转换
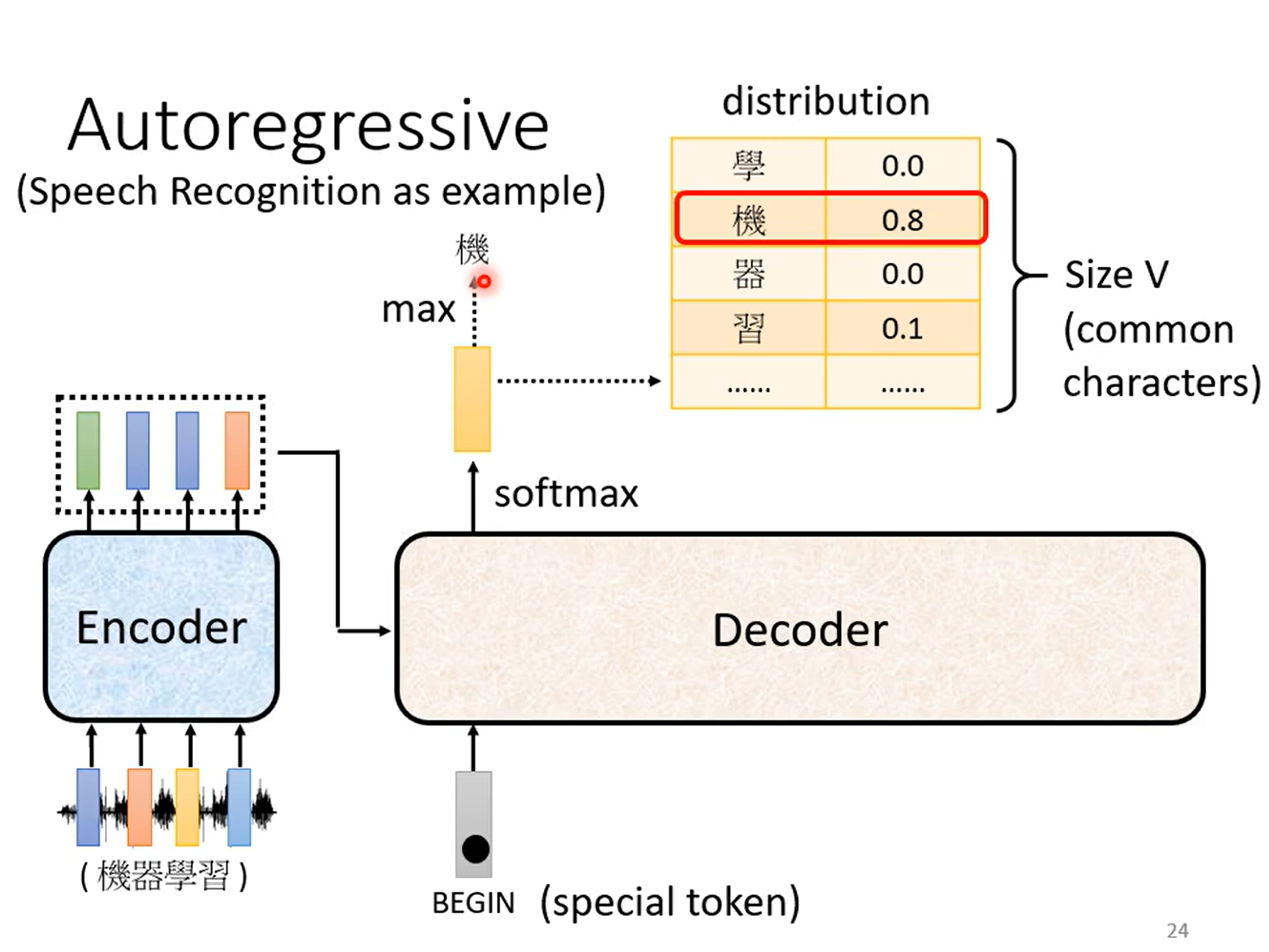
输入用$\text{One Hot}$进行编码,向量大小为输出集的大小
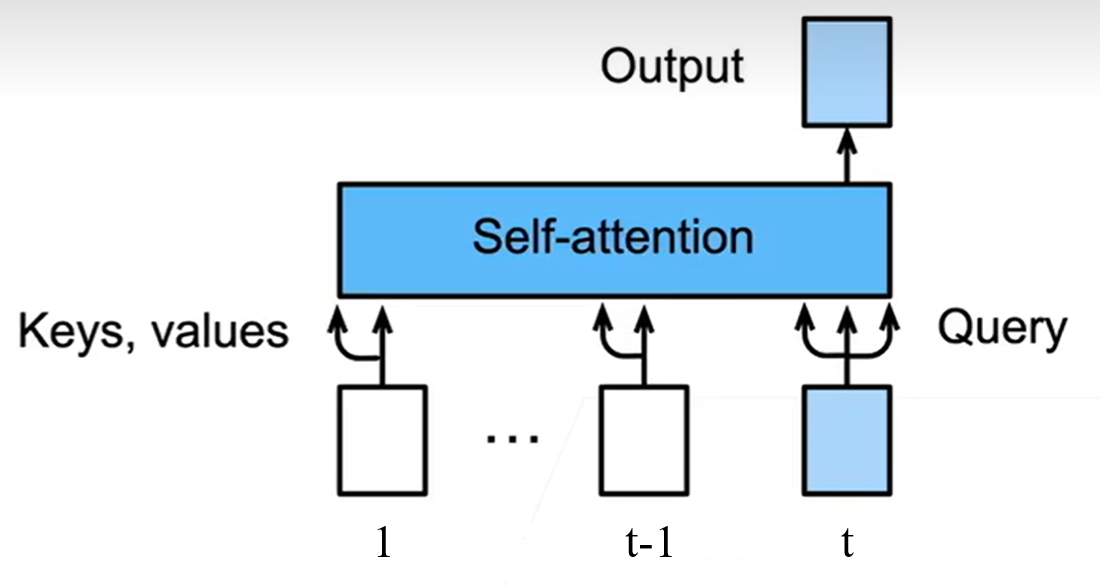
只把过去的output来作为$\text{keys,values}$
训练时每次把未来的输入$\rm Mask$一下
每次只query$t$时刻的输出,同时decoder放入$1\sim t$的输出
从而得到$t+1$时刻的输出
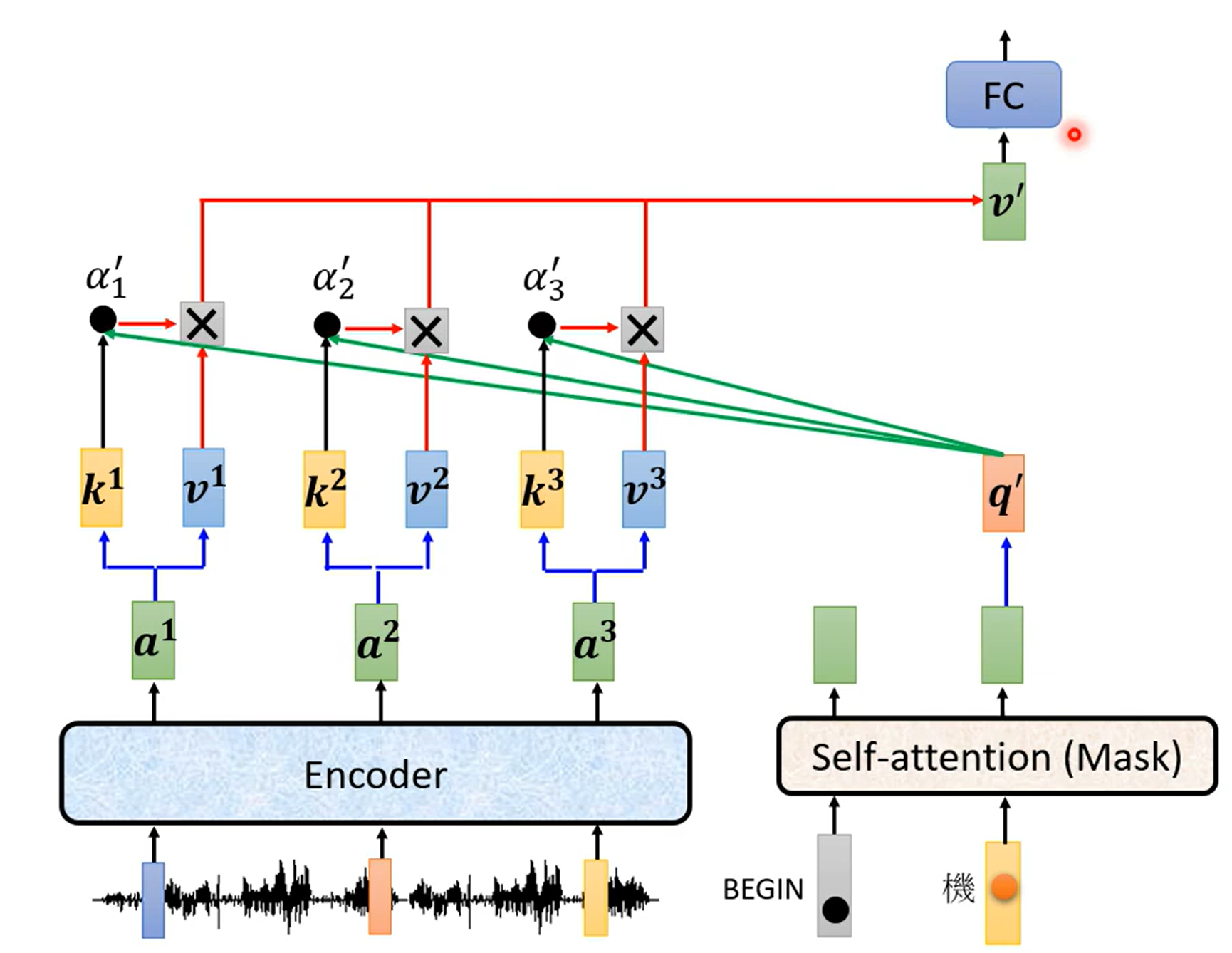
$K,V$来自Encoder而$Q$来自Decoder
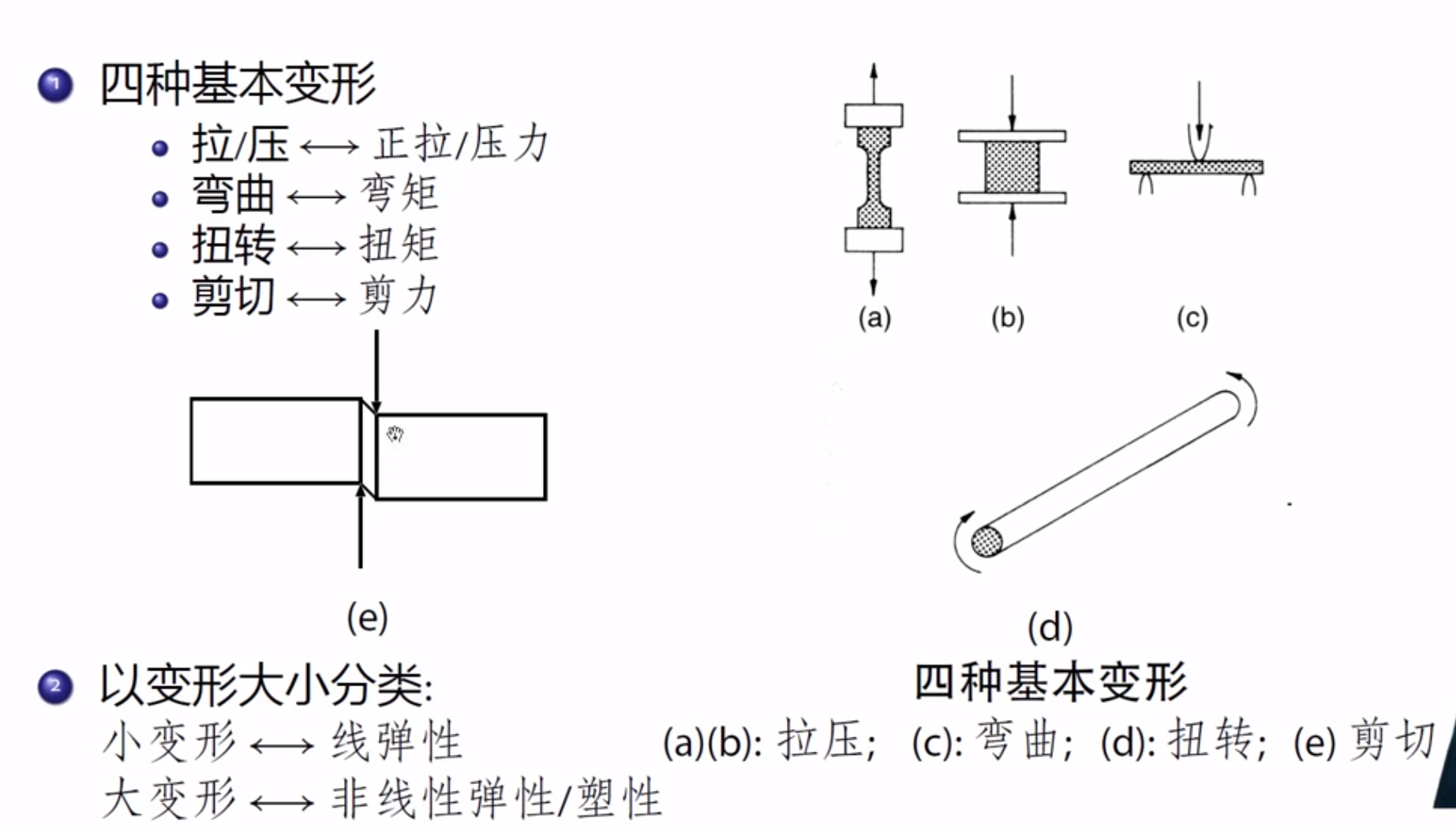
胡克定律
关系,泊松比$\nu$
只在一个方向有线应变有横向变形效应
广义胡克定律
特别的,对于平面应力状态,有
衡量材料力学性能的指标
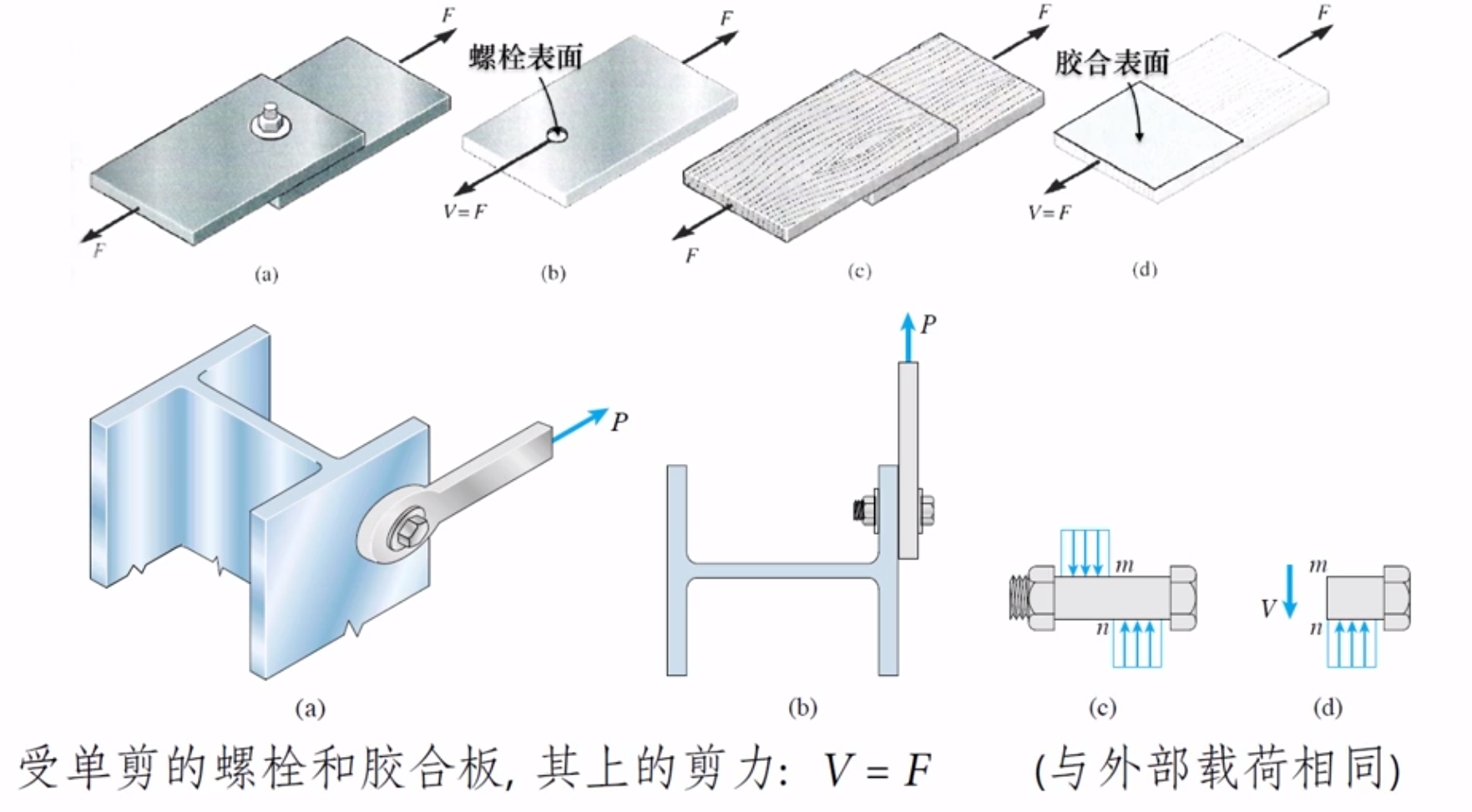
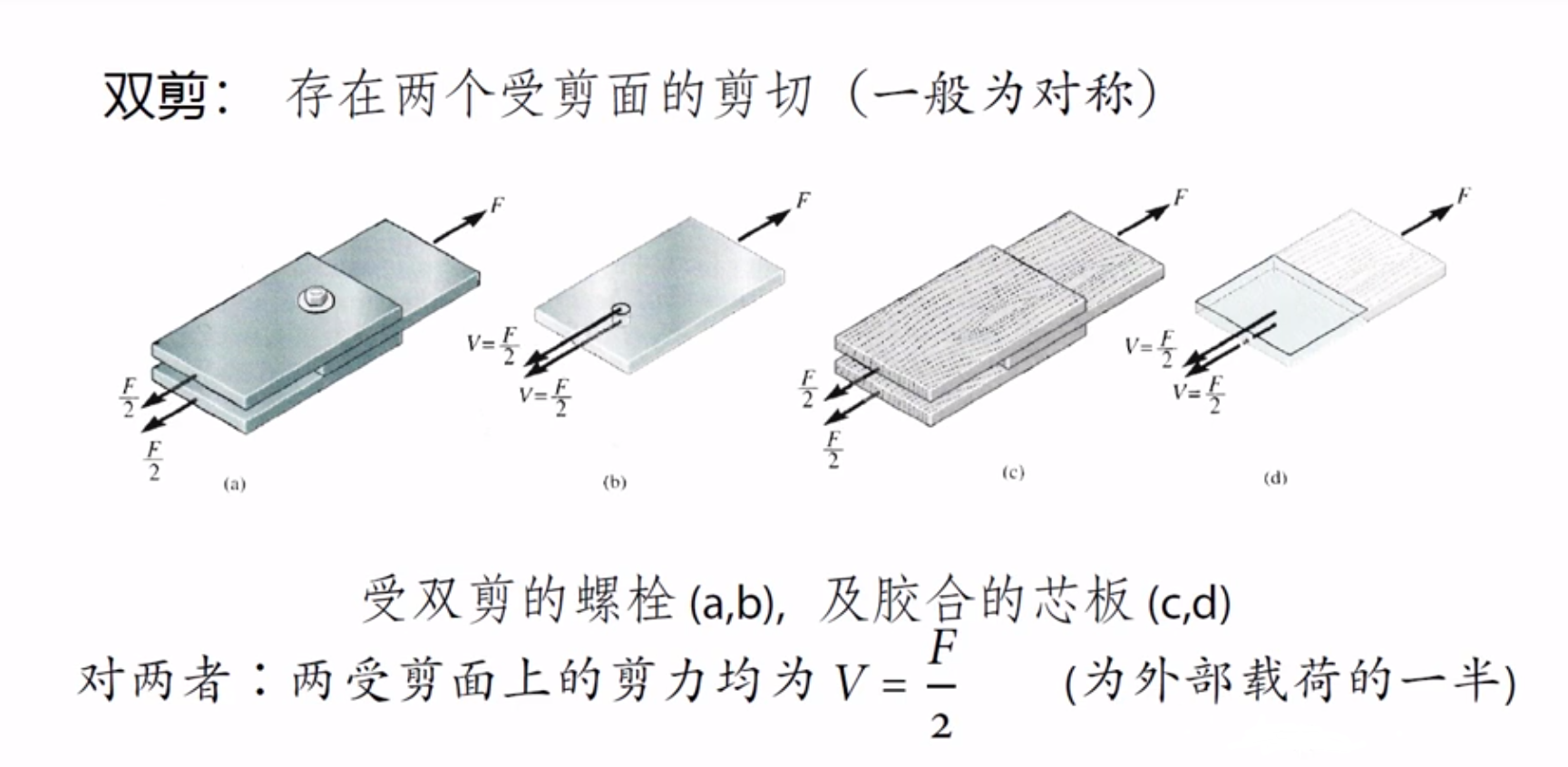
同时存在挤压
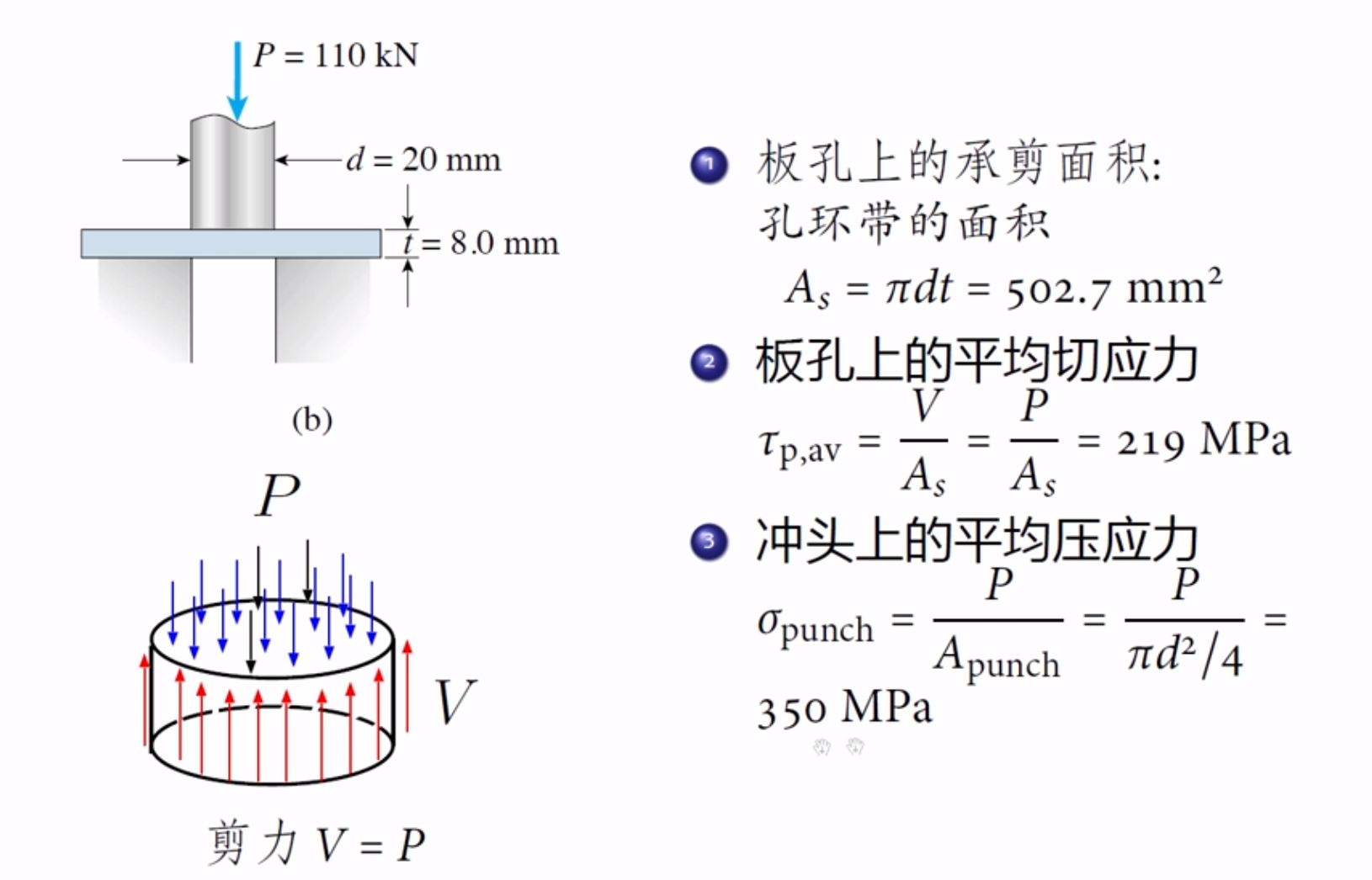
计算切和压只需要判断力和面积
剪切:剪力对应接触面积
挤压:压力对应正交面积
截面上的扭转
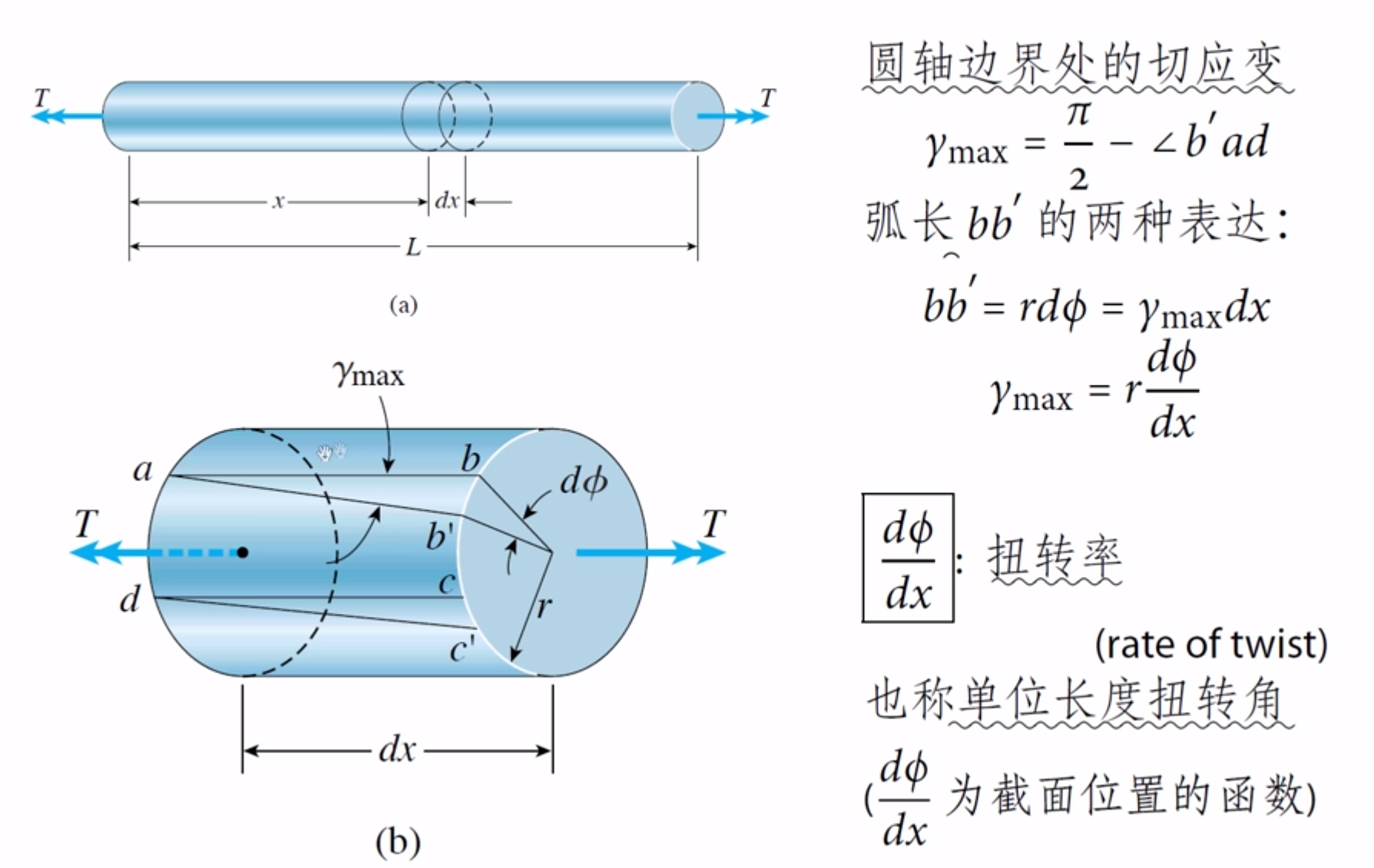
切应力
其中$I_p$为截面的极惯性矩
对于圆
空心
对于半径处(表面),截面系数为
单位长度扭转角
单位为弧度,要转角度,则
强度条件
刚度条件
计算时画出扭矩图
简支梁
两端分别为固定铰支座和活动铰支座
悬臂梁
一端为固定端一端为自由端
外伸梁
至少有一个铰支座不在梁端部
利用力的平衡可以得到剪力和弯矩
同时注意剪力以顺时针为正
弯矩以凹为正,同时弯矩图画在拉的那一侧(朝下)
需要标明正负
中性层为基准
正应力随高度呈线性变化,正比弯矩,反比于形心主惯性矩,两侧正应力一拉一压,总是同时存在
惯性矩计算
对矩形截面
空心圆形
同时利用对称性来计算
四矩式
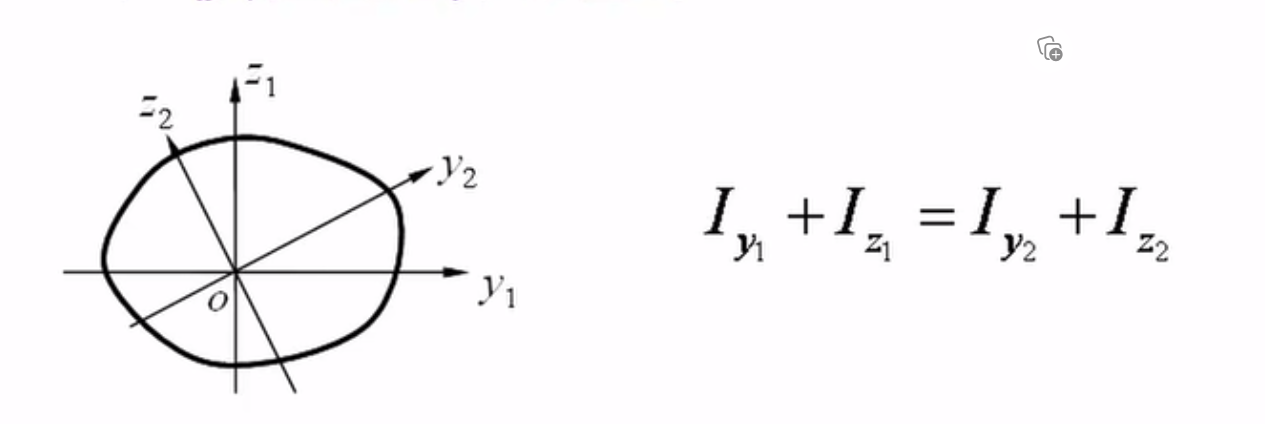
其中$S_z^*(y)$为静矩
利用形心来计算,$b$为厚度
掌握计算校核设计截面的方法,分析危险截面
挠度$y$,为相对的位置变化
则利用微分方程得到
进行积分,带入边界条件尽可能早的确定常数
如固定端$\theta,y=0$,铰链左右转角相等 等等
利用叠加法首先将所有的载荷等效到一段
用相差一个刚体位移的方法进行计算
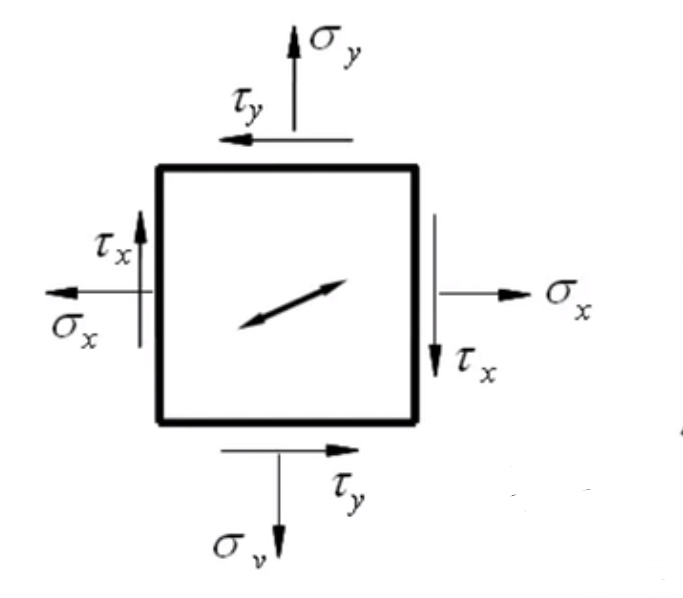
正应力以拉为正,压为负
切应力以外法线顺时针旋转
对任意角度,有
则有
相互垂直截面上的正应力之和为常数
可画出应力圆求解
对于切应力极值,与主平面呈45度角,此时正应力为
对于空间应力,$\sigma_z\ne0,\tau_z=0$
所以$z$已经是主平面,求处另外两个主应力,画在一起
为三向应力圆
主应力按照从大到小的顺序排列后
四个强度理论
还有莫尔强度理论
特别的,对于单向
更特别的
切应力主要为扭矩产生,正应力主要为弯矩产生
分别在$x,y$方向上画弯矩图
计算最大应力时,分解后叠加
注意$M_y$为$F_z$产生
同理挠度也叠加
将心的力$F_2$等效成
转换成一个正应力和弯矩
对于不同支承条件,长度系数不同
如果两端铰支,都可以转动(角度任意变化)
或者两端固定另一端可以横向移动
若一端自由另一端固定
两端固定
一端固定,一端铰支
所以临界压力
引入柔度的概念
其中$i=\sqrt{\frac {I_z}{A}}$,截面对失稳弯曲时的中性轴的惯性半径
所以临界应力公式为
则柔度需要满足
对于铸铁$\rm Q235$
对于中长杆,可以使用经验公式
或者
将向量向其他基向量上进行投影并减去分量
最后再单位化即得到标准正交基
求解行列式为零得到对应的特征方程,即可求出特征值再把特征值代入可求得特征向量
如果特征值各不相同则特征向量线性无关
若矩阵满足矩阵方程
则它的特征向量也满足
同理
逆矩阵的特征值为倒数,特征向量一样
伴随矩阵特征向量也一样特征值为
满足
相似矩阵的特征多项式相同特征值也相同
若$A$为对角矩阵则
对称矩阵的特征值为实数,且一定可以对角化,任意两个不相等的特征值对应的特征向量一定正交
矩阵$P$可通过对特征向量组进行标准正交化得到
代数重数为$(\lambda-\lambda_i)^m$,几何重数为特征向量生成线性空间的维数
几何重数$\le$代数重数
可对角化则代数重数等于几何重数,即矩阵$P$满秩,特征向量足够
化为对称矩阵来表示
可逆变换
则如果有可逆矩阵,使得
则合同
只有平方项
正交变化则和化对角一样
实对称矩阵$AB=BA=(AB)^T$才讨论正定
二次型恒大于0,正特征值的个数就是正惯性指数,则正定为
看$\lambda$正负
$A+B$正定,$BAB$正定,$A^{-1},A^*,A^m,kA$正定
若$AB=BA$则
只有对称矩阵,相似一定合同(因为正交相似)
对称矩阵可对角化,代数重数=几何重数则可对角化
等价$\Leftrightarrow$秩相等
$A\Leftrightarrow B$则对应的齐次线性方程组同解
$R(A)=R(AA^T)$
像空间的维数用矩阵表示的秩$r$来算
核空间的维数$n-r$
秩一矩阵,各行成比例,则$A=\alpha\beta^T$
则唯一非零秩为$\text{tr}(A)=\beta^T\alpha$
可对角化则$\beta^T\alpha\ne0$